温度作用下变径管道的应力应变分析
2017-09-12薛景宏储阳华
薛景宏,储阳华
(东北石油大学 土木建筑工程学院, 黑龙江 大庆 163318)
温度作用下变径管道的应力应变分析
薛景宏,储阳华
(东北石油大学 土木建筑工程学院, 黑龙江 大庆 163318)
管道在发生热胀冷缩效应时会产生热应力,由于热应力的存在使管道发生伸缩挤压从而使管道发生变形,在管道变径处可能发生破坏。通过有限元软件ANSYS进行建模分析,采用8节点solid实体单元模型模拟变径管道。研究同心变径管道在温度作用下最易发生破坏的薄弱位置、温度对变径管道的影响以及温差对变径管道的影响。结果表明:在温度作用下,变径管道薄弱位置位于管道的变径处周围;变径管道的极限应力和管道温度、温差都有联系。该研究为热力管道的设计提供参考,使得热力输能变径管道设计合理节能。
同心变径管道;有限元软件;温度;温差;薄弱位置
目前,管道工程已经成为了各个国家和地区的民生工程,成为了一项生命工程[1]。在许多地方都已经离不开管道的应用,比如供暖工程、天然气运输、市政工程等。管道的诸多优势决定了其可以作为国家经济发展和居民生活的重要工程项目。但是,管道自身制作工艺的差异为正常作业和环保节能带来了挑战,人们对这类问题也越来越重视。
通过对管道节能环保分析,国内外诸多学者在管线的节能方面做了大量的理论、实验研究有限元模拟分析,取得了许多有用的研究成果。在供热供暖中通常需要考虑管道变径的问题[2-4],很多关于管道的研究成果都是针对直管道得出了结果,但在工程实践中,很多的管道避免不了的要变径。笔者在前期学者的研究基础上,通过有限元仿真软件对变径管道模型进行了模拟[5-7],可以为管道的设计提供很好的参考。研究了变径管道在温度作用下的薄弱位置、温度对管道热应力的影响、温差对管道热应力的影响。
1 有限元模型建立
1.1 变径管道边界条件
在工程设计中,为了使变径管道在作业时处于稳定状态,对于变径管道设计都有一定要求。本文选用管道材料为API5LX60,采用8节点solid单元建立同心变径管道模型进行分析。对变径装置处的变径角度取90°,管道两端采用固端约束,同时在变径处采用固端约束,应用焊接连接。
1.2 几何模型和网格划分
本文选用API5LX60进口钢材作为研究材料。该材料的应力应变关系为输油气钢质管道设计规范中的三折线简化模型,见图1。大直径管道16 m,小直径管道16 m,管道总长度是32 m,采用8节点solid单元建立管道模型进行数值模拟分析,通过ANSYS有限元软件划分网格功能对管道进行网格单元划分,沿管道轴向方向为0.5 m一个单元,沿管道圆周方向划分32个单元。变径管道有限元模型如图2所示。

图1 应力应变关系三折线模型
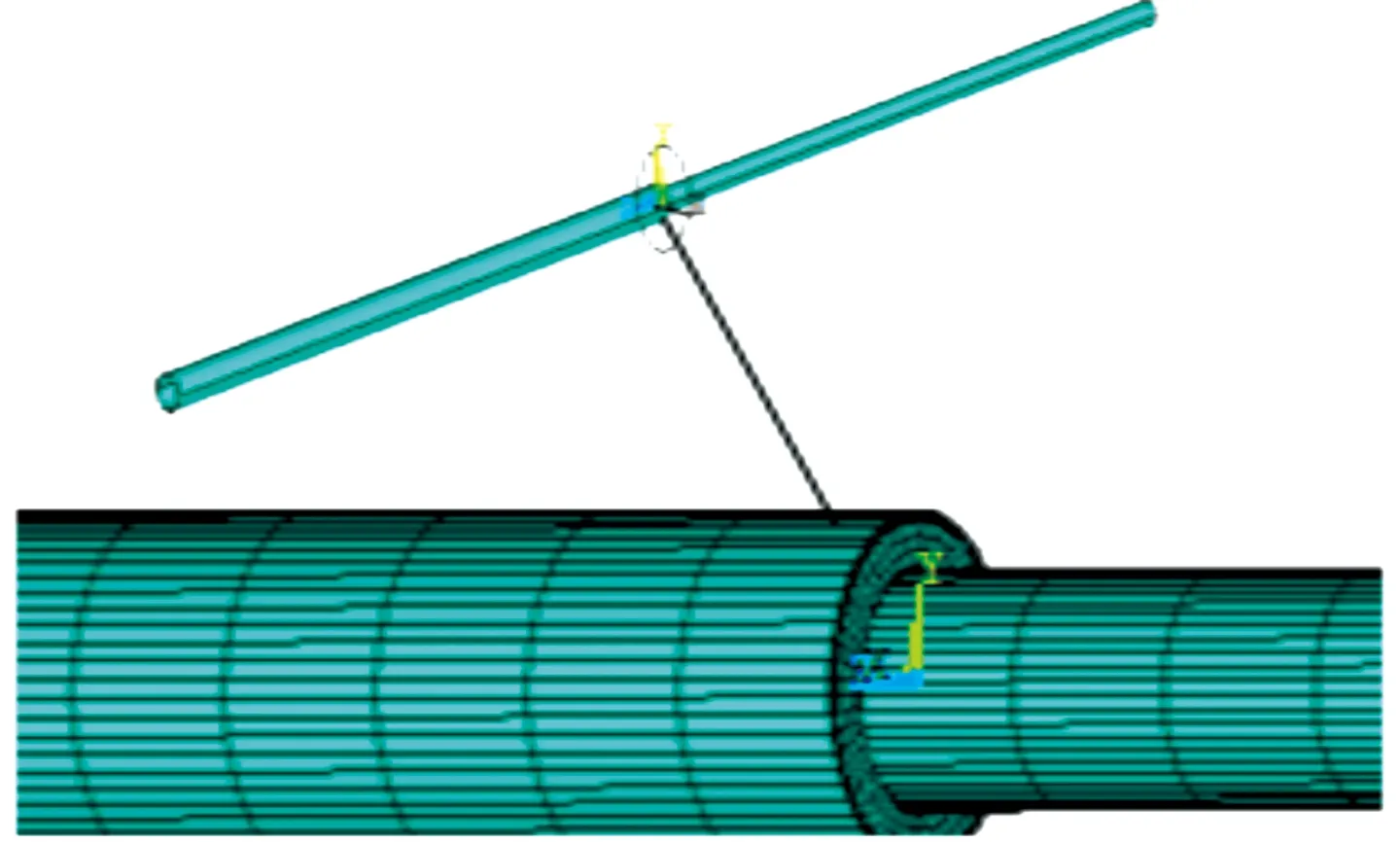
图2 变径管道有限元模型
2 数值模拟结果分析
2.1 温度变化下对管道参数确定
1) 温度变化对管道膨胀系数影响
钢材在温度作用下,钢材的膨胀系数会发生相应的变化。根据我国《钢结构设计规范》规定,温度变化对钢材膨胀系数取值影响可忽略,均取常数αs=1.25×10-5,而美国和澳大利亚则建议采用随温度变化的膨胀系数值。具体系数计算公式[8-9]如下:
αs=0.8×10-8(TS-20)+1.2×10-5
20 ℃≤TS≤750 ℃
(1)
αs=0, 750 ℃≤TS≤860 ℃
(2)
根据式(1)计算得到温度TS与膨胀系数αs关系值,见表1。
由于本文中所取温度均低于100 ℃,通过式(1)计算可得的热膨胀系数与我国规范拟合较好,故温度低于100 ℃时,αs的取值为1.25×10-5,即在本文索取的温度中,温度对刚才的影响很小,可以按照与温度无关取值。

表1 αs和TS关系
2) 温度变化对管道热传导系数影响
热传导系数取值以标准单位钢材作为基准,在实际工程计算中,钢材的厚度不厚时,可以采用假定的与温度无关的热传导系数值。本文热传导系数[28-29]λs取值为45。
3) 温度变化对钢材弹性模量影响
在温度变化环境下,钢材结构的材料性能受温度影响明显,ECCS[31]中规定其影响方式为:
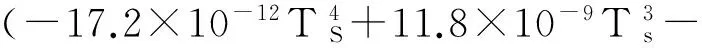
0 ℃≤TS≤600 ℃
(3)
式中:E是钢材常温下的弹性模量(N/mm2);ET是一定温度时钢材的初始弹性模量(N/mm2)。
根据式(4)计算钢材的弹性模量,结果如表2所示。

表2 Er与TS关系
通过表2可以看出:温度变化在100 ℃以内时,温度变化对钢材的弹性模量影响很小,故可以按照与温度无关取值,取值为2.1E+11 N/mm2。
4) 温度变化对钢材屈服强度的影响
钢材结构的屈服强度可以根据以下公式进行确定:
(4)
(5)
本文中所选取温度在100 ℃以内,选择式(4)进行计算,可得fyT=fy。
5) 其他参数
泊松比受组成成分与施工工艺影响较小,常温下通常取0.27~0.30,其受温度影响也很小,可以按照与温度无关取值,本文μs=0.3。本文钢材料结构单位密度通常取为ρs=7 850 kg/m3。
2.2 变径管道应变分析
通过有限元软件ANSYS建立并分析中砂场地上变径管道,选取API5LX6进口钢材。大管径D1=0.762 m,壁厚δ=0.023 8 m;小管径D2=0.508 m,壁厚δ=0.023 8 m;弹性模量E=2.1×1011Pa,泊松比μ=0.3;传热系数为45 W/(m·K),热膨胀系数为1.25×10-5,屈服强度为520~620 MPa。在变径管道内部施加温度为70 ℃,在变径管道外部施加温度为20 ℃,通过有限元软件ANSYS模拟对供热供暖管道进行应力应变分析,结果见图3~5。通过有限元软件模拟分析得出变径管道最大拉压应力点和最大拉压应变点都位于管道变径处附近。最大拉应变为0.959×10-2,最大压应变为-1.028 3×10-2,最大拉应力为0.672×10-2Pa,最大压应力为-0.444×1010Pa,都发生在变径处。

图3 变径管道沿轴向温度分布
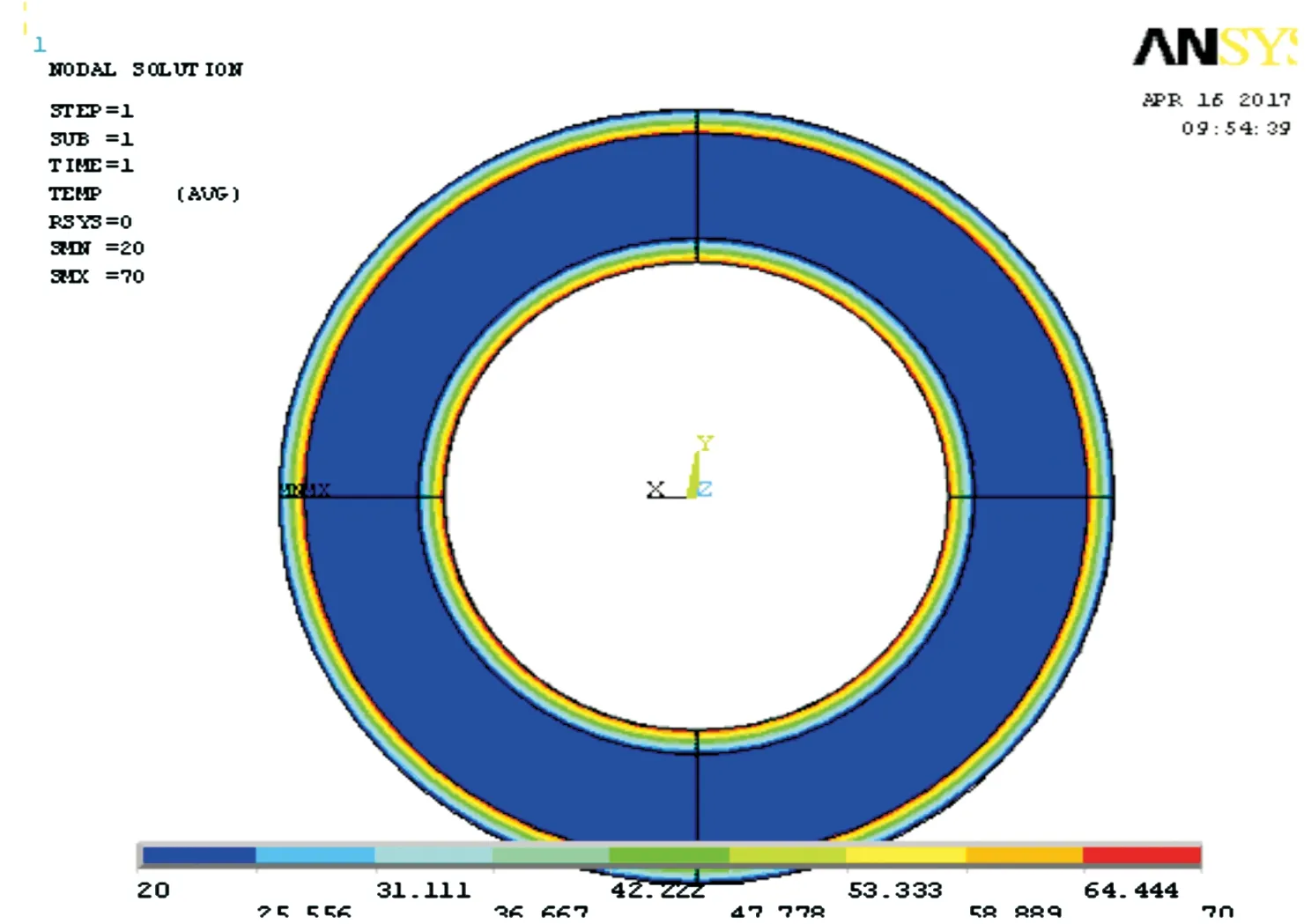
图4 变径管道沿径向温度分布
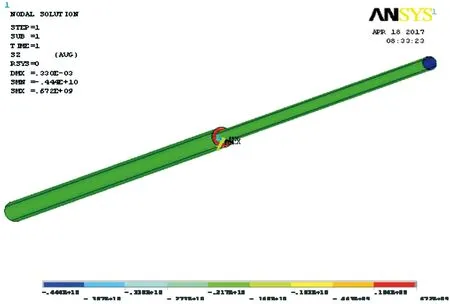
图5 变径管道轴向拉(压)应力云图

图6 变径管道轴向拉(压)应变云图
2.3 温度对变径管道的影响
通过有限元软件ANSYS建立并分析中砂场地上变径管道,选取API5LX60型进口钢材。大管径D1=0.762 m,壁厚δ=0.023 8 m;小管直径D2=0.508 m,壁厚δ=0.023 8 m;弹性模量E=2.1×1011Pa,泊松比μ=0.3;管道埋置深度H=2 m;传热系数为45 W/(m·K),热膨胀系数为1.25×10-4,屈服强度为520~620 MPa。分别模拟了变径管道在温差为5 ℃,变径管道外部温度为20 ℃、25 ℃、30 ℃,对应的管道内部温度为25 ℃、30 ℃、35 ℃下变径管道下的变径管道的应力应变分析。
通过ANSYS有限元模拟研究发现,在温差一定的情况下,变径管道随着温度的升高,最大拉压应变点的位置都大约位于变径装置的周围附近。
变径管道在温度影响下的轴向最大拉、压应变如表3、图7所示。

表3 温度影响下管道最大拉、压应变值
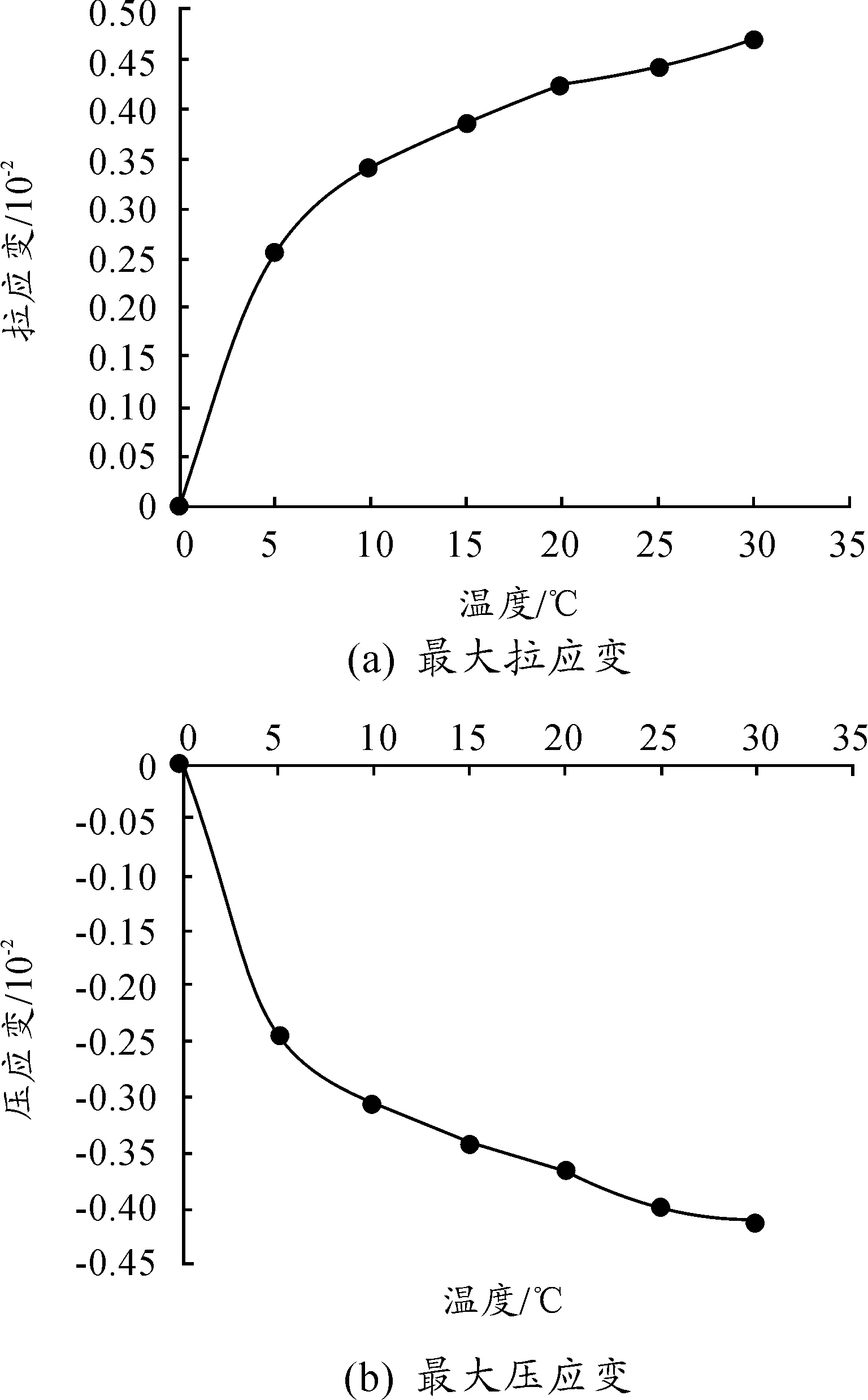
图7 温度不同,不同变径管道最大拉、压应变值
有限元模拟结果表明:在变径管道的内外温差一定的情况下,温度对变径管道的影响较大,管道的最大拉(压)应变都随着温度的增加而增加,变径管道的拉应变变化值比管道压应变变化值要大。
变径管道在温度影响下的轴向最大拉、压应力如表4、图8所示。

图8 温度不同变径管道最大拉、压应力值
有限元模拟结果表明:在变径管道的内外温差一定的情况下,变径管道在变径处附近的拉压应力达到最大值,同时随着温度的增加,变径管道的拉、压应力随之增加。
2.4 温差对变径管道的影响
通过有限元软件ANSYS建立并分析中砂场地上变径管道,选取API5LX60型进口钢材。大管径D1=0.762 m,壁厚δ=0.023 8 m;小管直径D2=0.508 m,壁厚δ=0.023 8 m;弹性模量E=2.1e11Pa,泊松比μ=0.3;传热系数为45 W/(m·K),热膨胀系数为1.25×10-4,屈服强度为520~620 MPa。分别模拟变径管道在不同温差下的最大拉(压)应力,进行温差为10 ℃、20 ℃、30 ℃、40 ℃、50 ℃下的变径管道的应力应变分析。
变径管道在温差影响下的轴向最大拉、压应变值如表5、图9所示。
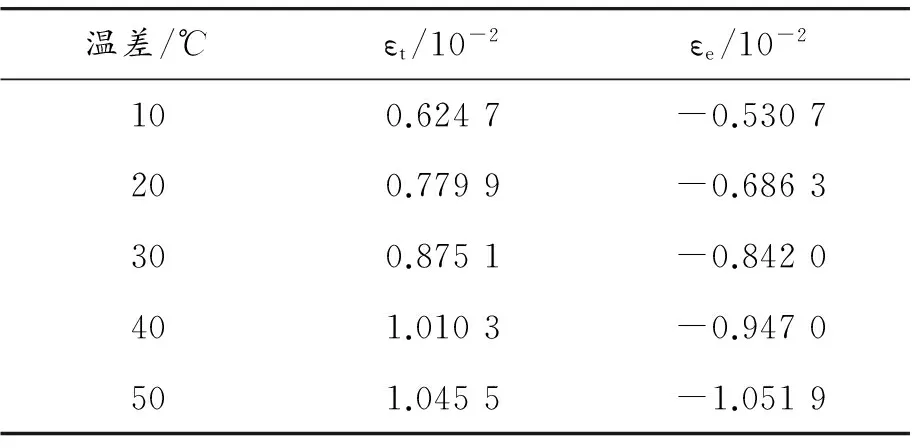
表5 温差影响下管道最大拉、压应变值
有限元模拟结果表明:温差对变径管道的影响很大,变径管道在变径装置附近的极限拉压应变随着温差的增加而增加。
变径管道在温差影响下的轴向最大拉、压应力值如表6、图10所示。
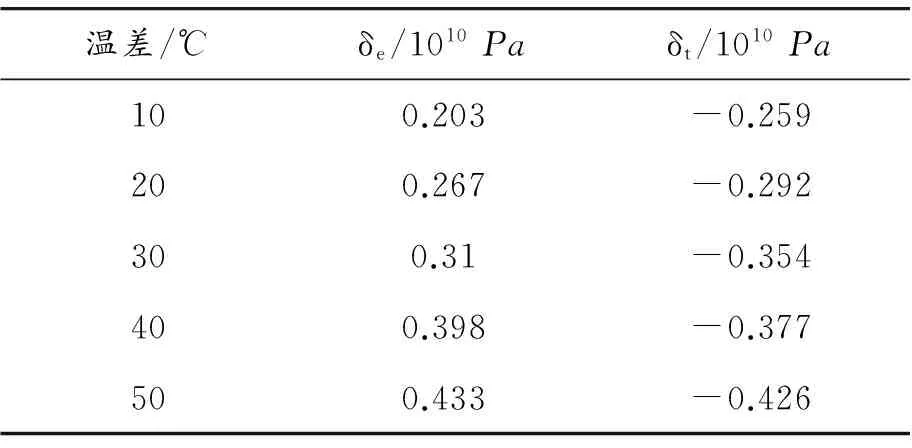
表6 温差影响下管道最大拉、压应力值
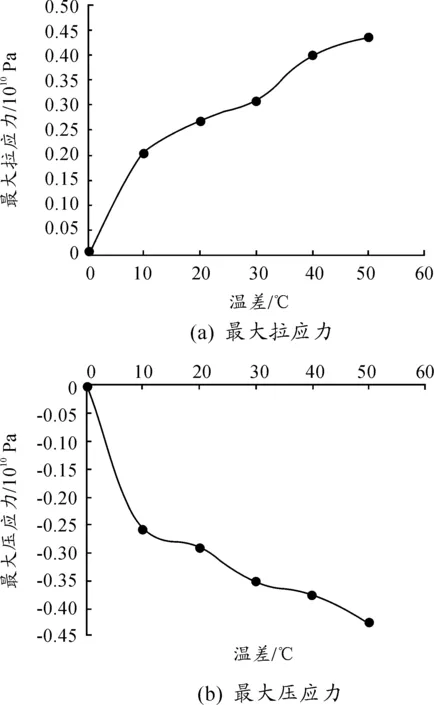
图10 温差不同变径管道最大拉、压应力值
有限元模拟结果表明:温差对变径管道的影响很大,变径管道的拉、压应力值随着温差的增加而增大,同时在在变径装置附近的极限拉、压应力值随着温差的增加而增加。
3 结论
研究表明:变径管道的薄弱位置是在大直径管道和小直径管道连接处附近;温度的变化对变径管道影响较大,当温差一定下,变径管道应变随着温度的增加而增加;温差对变径管道具有一定影响,变径管道的拉、压应变随着温差的增加而增加,极易发生断裂。在实际工程中,需要加强对变径管道在变径装置处的抗拉、压设计。本文研究对工程中管道变径装置设计具有指导意义。
[1] 赵成刚,冯启民.生命线地震工程[M].北京:地震出版社,1994.
[2] 王宇.变径管道对冷热原油顺序输送混油的影响[J].山东工业技术,2017(5):266.
[3] 薛景宏,娄彦鹏.跨断层埋地变径管道抗震分析[J].黑龙江科技大学学报,2016(3):272-276.
[4] 黄凯,郭晋川,姚瑶. 管道变径调压效果试验[J]. 广西水利水电,2014(2):6-8.
[5] 臧延旭,杨寒,白港生,等.长输管道变径清管器研究进展[J].管道技术与设备,2013(6):45-48.
[6] 李勇,朱秀苹.气力输送中变径管道系统设计的研究[J].起重运输机械,2008(10):25-27.
[7] 方明. 管道热应力分析实例[J]. 广州化工,2005(2):49-51.
[8] European Committee for Standardization, ENV 1993-1-2, Eurocode 3, Design of Steel Structures, Part 1.2: Structural Fire Design [S].
[9] European Committee for Standardization, ENV 1994-1-2, Eurocode 4, Design of Comosue and Concrete Structures, Part 1.2: Structural Fire Design [S].
(责任编辑 刘 舸)
Stress-Strain Analysis of Reducing Pipe Under Temperature
XUE Jinghong, CHU Yanghua
(College of Civil Engineering and Architecture, Northeast Petroleum University, Daqing 163318, China)
In the event of thermal expansion and contraction in the pipeline, thermal stress is generated. Due to the existence of thermal stress, the pipe is stretched and contracted to cause deformation of the pipe and damage may occur at the pipe diameter. In this paper, the finite element software ANSYS is used for modeling and analysis, and the eight-node solid solid element model is used to simulate the variable pipe. The influence of temperature on the diameter of the pipeline is studied. The influence of the temperature difference on the variable pipe is studied. The results show that the weak position of the variable pipe is located around the change of the pipeline under the action of temperature. The limit stress of the variable pipe is related to the temperature and temperature of the pipeline. The study provides a reference for the design of thermal pipelines, making the heat transfer variable diameter pipeline design reasonable energy saving.
concentric variable pipe; finite element software; temperature; temperature difference; weak position
2017-05-22 基金项目:国家自然科学基金资助项目(51578120)
薛景宏(1968—),男,吉林梨树人,博士,教授,主要从事防震减灾工程研究,E-mail:xjh0459@126.com。
薛景宏,储阳华.温度作用下变径管道的应力应变分析[J].重庆理工大学学报(自然科学),2017(8):51-56.
format:XUE Jinghong, CHU Yanghua.Stress-Strain Analysis of Reducing Pipe Under Temperature[J].Journal of Chongqing University of Technology(Natural Science),2017(8):51-56.
10.3969/j.issn.1674-8425(z).2017.08.008
TV67
A
1674-8425(2017)08-0051-06
