基于盒式鲁棒的主动配电网经济调度
2022-04-06张玉晓谢加新李克豫
张玉晓,谢加新,李克豫
(国网河南省电力公司周口供电公司,河南 周口 466000)
0 引言
经济发展带来了能源匮乏和环境污染问题,迫切要求人们寻找替代能源。分布式电源清洁、成本低等特点恰恰满足人们的需要,未来配电网接入大量的DG(分布式电源)将成为发展趋势[1]。然而清洁能源具有较强的波动性,制定相应的控制策略,因此以合理高效地应对其不确定性,满足配电网的可靠性需求,具有重要的价值和意义。
目前,在对DG和负荷不确定性特性的建模优化方法主要有:随机规划、模糊规划以及鲁棒优化[2-4]。随机规划即随机变量受概率控制来描述出力的不确定性,但实际应用中有计算量大且耗时耗力,概率分布不确定等缺点[5]。模糊规划用模糊变量描述不确定性,由隶属度函数衡量约束的满意程度来求解,结果受样本数据和决策者主观性影响较大[6]。鲁棒优化理论能有效解决不确定问题,其按照一种集合约束的形式来描述不确定参数问题,使不确定变量集中于所建集合中,以期取得所有的可能值。鲁棒优化的关键在于选取不确定集,一般有盒式、椭圆、多面体等形式[7],相对于其他两种形式,盒式不确定集对求解的问题有更好的收敛性,求解速度快等特点,广泛用于线性规划、二阶锥规划[8]等问题。考虑到实际问题的需要,本文采用盒式鲁棒优化。常规的盒式鲁棒优化往往以牺牲部分经济性为代价来提高系统的鲁棒性,使得结果偏于保守。基于可调节鲁棒优化方法能有效弥补常规鲁棒优化的不足,更好平衡系统的经济性和鲁棒性。文献[9-11]都通过盒式集合对不确定性进行约束,建立了可调节的鲁棒优化模型。但只涉及配网中的发电与负荷的平衡问题,未考虑电网运行的网络损耗和电网运行过程中的安全约束。文献[12]经过线性化潮流,对电压电流安全约束建立了鲁棒模型,但缺乏对系统鲁棒性的调节。文献[13]建立了以网损为目标函数的三相配电网的可调鲁棒优化模型,基于配电网的实际情况,未对负荷的不确定性给予考虑。
主动配电网数学模型由于决策变量众多,是一个复杂多变的整数规划问题,目前求解方案多集中于如遗传算法、BP神经网络算法、粒子群算法等智能算法或传统的二次规划等方法。但智能算法易陷入局部最优解,传统算法求解速度慢。以二阶锥规划为代表并结合Distflow支路潮流模型的凸优化求解方法得到了广泛的应用[14-18]。
综合以上问题,本文考虑DG和负荷的不确定性,且保证配电网的安全运行约束,以变电站、MTG(微型燃气轮机)、SVC(静止无功补偿器)、ESS(储能装置)及IL(可中断负荷)等为决策变量,构造盒式可调节的鲁棒优化模型,以运行成本最小为目标函数,通过二阶锥规划将原模型的MINLP(混合整数非线性规划)问题,通过引入中间变量转化为MISOCP(混合整数二阶锥规划)问题,运用强对偶理论和拉格朗日变换对旋转备用容量进一步简化,通过CPLEX对IEEE 33节点系统仿真验证模型的合理性和正确性。
1 不确定区间可调鲁棒优化模型
基于对不确定因素对配电网优化结果的影响的考虑,鲁棒优化能够通过不确定集合对其合理描述,以保证各不确定元素加入系统后的可行性与可靠性。DG和负荷的不确定性恰恰可通过约束以满足系统安全稳定性的要求,为方便对不确定性的调节,以描述鲁棒优化保守度问题,现引入可调节参数,本文建立可调节鲁棒优化模型,一般模型可描述为:

式中:x为决策变量;ζ为不确定参数;U为有界不确定集。
考虑到DG和负荷的出力的波动性和周期性的特点,可根据典型地区的长期统计规律,建立不确定集U:

2 系统模型
2.1 优化模型目标函数
主动配电网的鲁棒优化模型目标在于实现经济效益最优,即目标成本最小。考虑到配电网的日前调度,此时上级电网,ESS、MTG、可控负荷及网络损耗等将参与功率调度,对DG不确定量的鲁棒化处理,额外增加了备用成本,现建立以主动配电网运行成本最小的目标函数为:
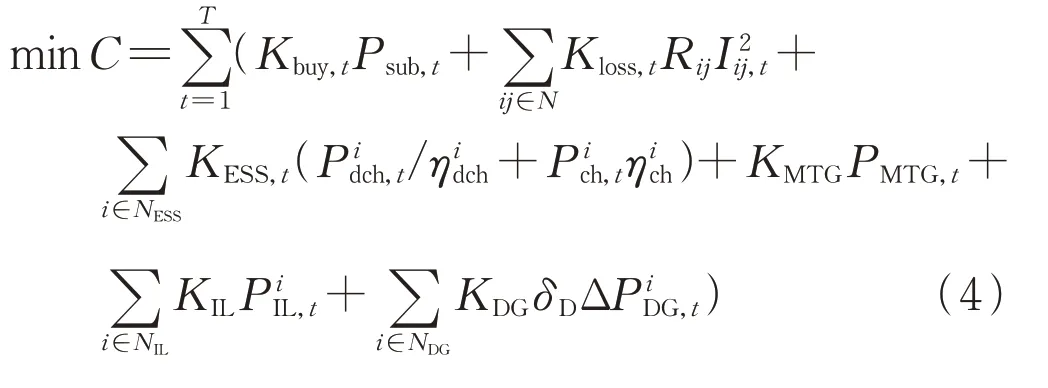
式中:N表示数量;分别为向上级电网购电量、ESS 的充放电功率、MTG输出的功率、可中断负荷中断量;Rij为网络电阻;Iij,t为线路流通的电流;为ESS 充放电效率系数;Kbuy,t、Kloss,t、KESS,t、KMTG、KIL、KDG分别对应功率的成本价格。
2.2 约束条件
1)潮流约束
参照文献[14],采用辐射状配网的Distflow支路潮流模型,并用二阶锥线性规划的方式进行等价变形。令:
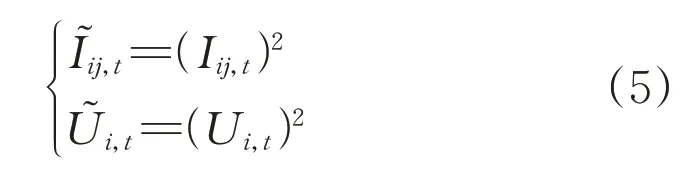
支路潮流模型变为:

松弛变形为:

电压电流安全约束:

2)功率平衡约束
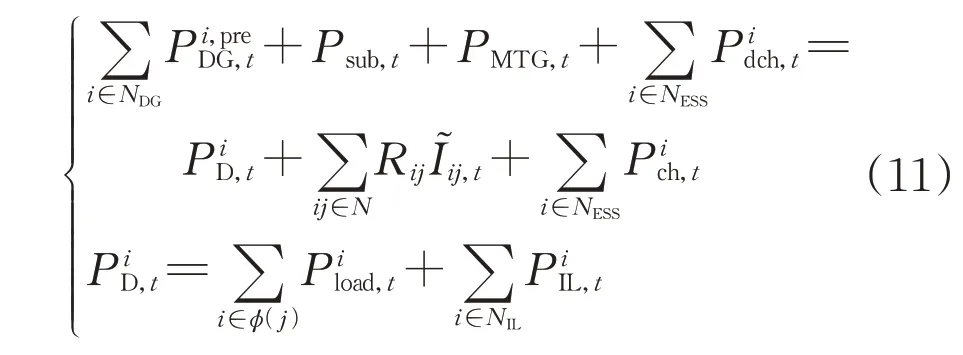
3)可中断负荷模型

4)ESS模型

5)SVC模型

6)MTG模型

7)DG不确定模型

8)变压器关口功率模型

9)旋转备用约束

式中:L为旋转备用率,一般取10。
2.3 可调鲁棒优化对等式模型
在配网确定性优化调度模型中,DG出力为预测值,没有考虑其不确定性,得到的优化方案在DG出力不确定波动条件下可能满足不了配电网安全运行要求。为此基于鲁棒优化方法,考虑DG出力的不确定性建立配网鲁棒优化调度模型,通过优化调度可控资源以消纳间歇性DG,保证在DG出力不确定波动条件下配电网的安全运行。
因此,采用线性化的鲁棒方法刨除模型中不确定性变量的方式,将式(11)、式(16)代入式(18)得:
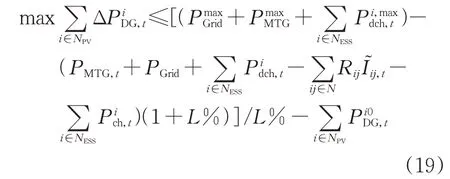
根据线性对偶理论:

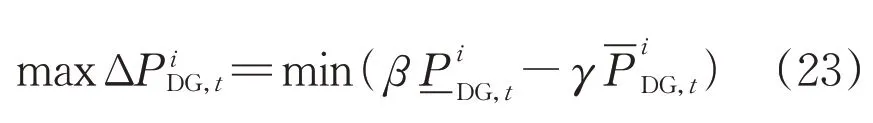
综上,鲁棒优化对等式为:

式中:α、β、λ均为拉格朗日系数。
最后,配电网鲁棒优化调度模型转化为不含不确定变量的鲁棒对等模型式。转化后的鲁棒调度模型只含确定变量的常规模型,可用商用软件CPLEX进行求解。
3 算例仿真
计算平台为系统硬件环境为Intei(R)Pentium(R)CPU J2900,4G 内存,操作系统为Win10 64bit,程序在Yalmip 上建模,于MATLABb R2016b环境下用CPLEX12.7算法包进行计算。
3.1 基础数据
采用修改的IEEE 33 节点系统仿真,算例中节点1为平衡节点,电压等级12.66 kV,功率基准取值为1 MVA,电压安全上下限设置为1.05 p.u.和0.95 p.u.。在节点13、18、27接入3种类型的光伏电站和节点31 接入风电机组,DG 和日负荷出力曲线如图1所示。

图1 负荷与DG出力曲线
考虑DG和负荷实际出力的最大偏差分别为预测出力的±30%、±10%,功率因数取0.95;选取3种不同的可中断负荷,代表居民、工业和商业用户,其接入位置和参数见表1;在节点4、17、29 分别接入MTG、ESS 等可控资源,参数见表2;SVC 接于节点5 和25,可调范围均为-0.3 Mvar—0.5 Mvar;购电电价如图2所示,网损电价为1 000美元/MWh,旋转备用容量惩罚成本系数为1 000。

表1 可中断负荷参数

表2 可调资源参数

图2 电价曲线
3.2 鲁棒性分析
采用可调鲁棒方法时,模型可以通过不同的不确定预算的取值求得的结果来分析论证系统的鲁棒性。现根据上文不同的不确定预算取值可设置3种情景,分别对应确定性模型,可调鲁棒模型和一般鲁棒模型。情景2分中间3种不同的不确定预算的取值如表3所示,为不同情景下各成本。对比情景1 与情景2 的各成本,可看出总体趋势下,可调鲁棒优化调度的总运行成本先低于后高于确定性优化调度,增加的成本主要来源于旋转备用容量交易成本,购电成本减少,网络损耗成本降低,可中断负荷补偿成本、微型燃气轮机成本则与确定性模型接近,储能运行成本几乎不变。ESS 和SVC 的投入对不确定负荷进行一定的平滑作用,增加了无功支撑能力,对比情景2和情景3可以看出,随着不确定预算的增加,旋转备用成本的明显变化,彰显了考虑越多的光伏出力和负荷不确定性,为保证系统的可靠运行,必须要付出更多的成本用以维系系统的稳定性,一般鲁棒模型过多追求系统的鲁棒性,常常以牺牲经济性来达到目的,采用本文不确定预算的方式对鲁棒性与经济性之间关系的修改,在保证运行可靠性的基础上经济型也有所提高。情景1与情景3的对比更加说明一般鲁棒模型为追求鲁棒性对经济性的牺牲。模型在一定程度上降低了网络损耗,但增加的总成本要求人们动态选择风光等可再生能源的接入。结合表3、情景1 和情景2 第3 种情况运行成本大致相同,绘出DG出力运行结果,如图3 所示,可以直观看出在运行成本接近的情况下,可调鲁棒模型将可消纳更多的DG出力,提高了分布式能源的利用率,可进一步减少弃风弃光造成的能源浪费,贴合低碳经济的政策方向,符合未来配电网接入更多可再生能源的趋势。本文所建立的可调鲁棒模型为电网合理调度提供了不同的选择。

表3 不同不确定预算下成本对比

图3 不同模型下DG出力运行结果
3.3 不同波动范围下鲁棒模型对比分析
分析所建模型在不同波动范围的优化结果,为简化分析过程,现仅分析DG 的出力的波动性,令确定性模型为DG 出力极端场景(即DG 出力的90%、80%、70%、60%)。通过对比,进一步分析可调鲁棒模型优化的优势。如表4不同波动范围下的不同模型规划运行成本对比结果。Γ=0、Γ=2、Γ=4分别对应上文的3种情景。

表4 不同波动范围下的规划结果
如表4所示,随着波动性的增加,由于情景1未计及旋转备用成本,在一定程度上具有降低成本的作用,但是,当DG 的波动范围大于0.2 后,模型无可行解,说明Γ=0时所对应的确定性模型应对DG 不确定性在极端场景下具有一定的局限性。情景2 和情景3 中,相对于情景1 都表现出对DG出力波动性良好的适应性,在波动性逐渐增大时,模型有可行解,且运行成本增加,说明DG出力波动越大对系统的成本影响越大,然而,相比于情景2,情景3成本过高,说明文中所建模型对降低系统运行成本具有较大的优越性,经济型更好。
为考虑模型对电压安全运行的影响,结合表4,画出DG 波动性为0.2 时的配电网电压最低点(节点33)的电压曲线如图4 所示。极端场景下确定性模型电压在负荷高峰期出现电压越下限情况,危及系统安全性,电压波动较大。对比发现,可调或一般鲁棒模型都满足电压安全约束,偏差较小,结合成本考虑在电压偏差允许的范围内文中所建可调鲁棒模型具有极大的优越性。另外,结合表3,可以看出考虑负荷的不确定性利于降低成本。所以调度在选择方案时,应考虑多方面的因素。

图4 不同优化方案节点33电压对比
综上,本文可调鲁棒优化模型,不仅增加了鲁棒性,增强了系统对不确定因素的对抗,在合理区间内也可起到降低成本的作用,一定程度上保证了系统的经济性,也保障了在不确定因素下系统的安全性,具有工程实用价值。
4 结论
针对含DG和负荷的不确定性的主动配电网规划,提出了一种基于盒式可调鲁棒优化的规划模型,将MINLP 问题,通过引入中间变量转化为MISOCP 问题,利用强对偶理论和拉格朗日变换简化优化模型。最后利用CPLEX对上述模型求解计算。算例仿真得出以下结论:
1)本文提出的可调鲁棒优化模型在综合考虑风电光伏等分布式能源及负荷的波动性,在合理区间内能有效降低购电成本、网损成本等,进一步降低运行成本,成本一定时能更多地吸收消纳分布式能源,协调了经济性与鲁棒性之间的平衡。
2)随着DG波动性的增大,可调鲁棒模型能有效动态调节,对于极端场景有更强的适应性,并进一步提高了系统运行的安全性和可靠性,满足实际配电网的需求。
3)今后研究方向有分析大规模DG接入对系统的影响、考虑接入设备的选址定容及其投资成本等。
