电动汽车接入对配电网运行特性影响的综合评估方法

张 帅，刘一欣，张宇轩，郭 力

（天津大学，天津 300072）

0 引言

随着电动汽车及其配套充电基础设施的大规模普及，配电网各节点电压和功率分布的随机性将进一步增强。在此情况下，有效地评估电动汽车接入对配电网运行特性的综合影响，对于开展配电网规划和优化调度有着重要的指导意义。

目前针对电动汽车接入对配电网运行特性影响的评估研究中，常用的配电网运行指标主要包括电压合格率、电压偏差率、线路重载率、负荷峰谷差、配变重载比、无功配置不合格率和短时负载率等［1-3］，主要采用概率的形式对各项指标进行评估，但通常是通过多场景得到不同场景下的潮流计算结果，再对这些结果进行统计得到对应的概率评估指标［4-5］。场景建模通过少量具有代表性的场景代替原始负荷和资源数据以降低计算量，但少量的场景分析无法全面准确地反映出配电网运行状态的分布情况，导致原始负荷和资源数据概率分布特性丢失，在计算准确性上相对较差［6］。概率潮流是处理配电网运行状态随机性的一种重要方法，可以准确反映配电网运行评估指标的概率特性。在概率潮流主要计算方法中，基于半不变量的级数展开法计算的效率更高，其在功率随机性较低时精度较高［7］，兼有其他计算方法的优点。然而基于运行基准点展开的半不变量法在含有电动汽车等具有较强功率波动幅值的负荷时，潮流计算难以保证足够的精度。

另一方面，电动汽车充电过程中与电网的连接形式主要分为集中式和分散式两种，由于配电网潮流与负荷的大小和分布位置有较大关系，因此在评估电动汽车充电负荷对配电网的影响时需要综合考虑所有节点上不同类型的充电负荷［8］，从整体出发展开评估［9］，因而需要对不同的元件赋予对应的权重。现有针对不同类型指标权重赋值的研究中，文献［10］通过灰色关联度提高人为主观赋权的一致性；文献［11］通过改进层次属性模型和标准间冲突性相关法确定不同指标的权重，提高了指标冲突性的识别能力；文献［12］通过改进熵权法提高了极端熵值情况下的权重配置合理性；文献［13］则通过最小二乘优化方法综合了主观权重与熵权法的优点。然而，上述研究仅对不同指标进行了权重分析，针对具体指标中不同元件的权重分配研究较少。以电压合格指标为例，当评估对象为配电网整体时，通常的做法为统计配电网中所有节点在所有运行时段的电压情况，将合格次数与总次数的比值作为电压合格指标［2，14］。然而，配电网出现电压问题的节点大多位于线路末端或分布式电源功率渗透率较高的节点［15］，当配电网节点数量较多时，电压不合格的节点在数量上占比较低，不合格运行状态的数据会被“淹没”在正常数据中，导致配电网的整体评估指标无法有效反映配电网中已经存在的运行问题。

为此，本文基于半不变量-级数展开方法进行概率潮流计算，采用分段线性化的方法降低潮流计算误差［16］，以随机变量的方差与期望值之比确定分段数，兼顾计算精度和计算效率。在此基础上，提出基于特征加权和熵权法的概率指标综合评估方法，结合评估对象的运行特性，对可能存在运行问题的节点或支路有针对性地赋予更高的权重，从而更有效地反映运行中存在的电压越限、线路过载等问题；利用熵权法对各线路概率评估指标进行加权计算，避免人为因素对权重计算造成影响，得到线路整体特性的综合评估结果。

1 概率潮流模型

1.1 运行基准点线性化

采用基于运行基准点的线性化方法对非线性潮流方程进行简化，得到负荷节点注入功率对电压幅值和支路有功、无功功率的影响，如式（1）所示：

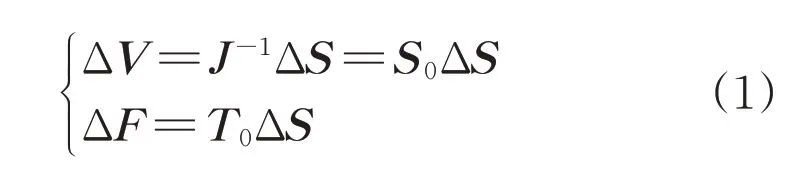
式中：ΔV表示节点电压变化量矩阵；J表示牛顿拉夫逊潮流计算中的雅各比矩阵；ΔS表示节点注入净功率较运行基准点的变化量矩阵；S0表示J的逆矩阵，为节点注入功率对电压的灵敏度矩阵；ΔF表示支路有功、无功功率变化量矩阵；T0表示节点注入功率对支路有功、无功功率的灵敏度矩阵，通过矩阵J和S0计算［17］。

1.2 考虑变量相关性的半不变量

采用相关系数矩阵处理实际配电线路中不同负荷节点的相关性，将存在相关性的随机变量表示为不相关随机变量与相关性矩阵的乘积［18］。则式（1）可转化为：

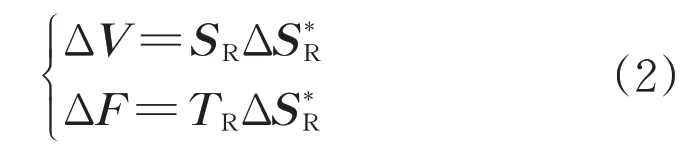
输入ΔV与扰动变量ΔS，则ΔF的各阶半不变量关系如式（3）所示：

1.3 分段线性化概率潮流

基于运行基准点线性化的潮流在扰动变量ΔS具有较大的波动性时，由于线性化模型本身的误差而导致计算不精确，通过分段线性化方法可以提高计算精度［17］。图1 中以分两段为例，可知在运行点增加后，分为两段分别进行潮流线性化时，在同样的ΔS变化量下，分段进行潮流线性化的计算误差ΔV会显著降低。两个区间内的灵敏度矩阵需要通过所在区间运行基准点的运行状态进行分别计算。

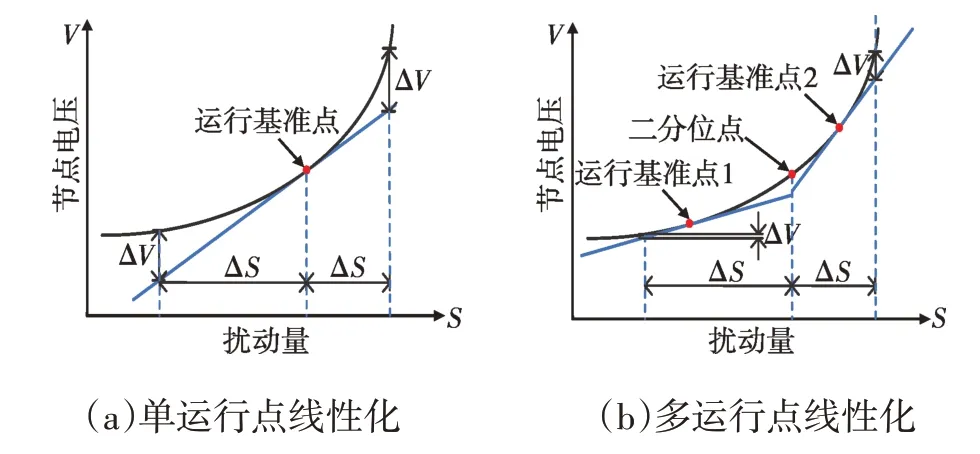
图1 分段线性化示意

划分的区域数量增加，计算量也成比例增加。在配电网中，考虑每个节点下的净功率波动特性时，每个节点的净功率变量都需要进行分段线性化，庞大的运行基准点数量将导致计算量过大，因此需要限制线性化分段数量。以随机变量的方差与期望值之比作为分段数的确定方法，分段区间边界采用随机变量的分位数确定，每个分段区间内的运行基准点选择所在区间内的随机变量期望值，具体如表1所示。

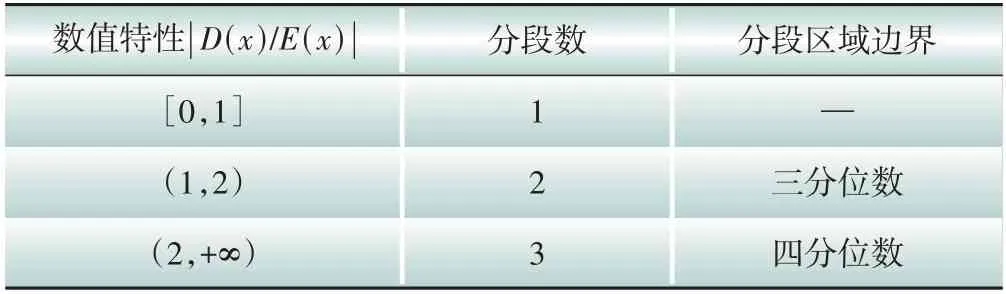
表1 节点净功率概率特性与线性化分段数量关系

表1 中，D(x)和E(x)分别为输入扰动变量ΔS的方差和数学期望，当|D(x)/E(x)|较小时，表示该扰动变量的波动性较小，此时分段数较少；当该比值较大时，适当增加分段数，有助于减少计算误差。

1.4 线路载流量概率分布计算

在潮流分析中常需要计算线路载流量约束，因此还需要对线路的视在功率进行概率建模。采用离散概率密度函数进行计算，可得到支路有功、无功功率平方的概率密度函数与累积概率分布函数，再通过卷积运算即可获得支路视在功率的概率密度函数与累积概率分布函数，如式（4）所示：

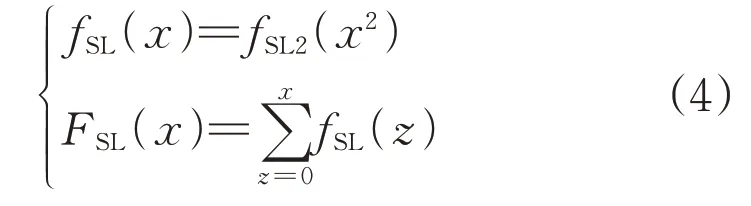
式中：fSL(x)表示支路视在功率的概率密度函数；fSL2(x2)表示支路视在功率平方的概率密度函数；FSL(x)表示累积概率分布函数；fSL(z)表示支路视在功率概率密度函数的离散值。

2 配电网运行特性概率指标评估方法

2.1 概率指标评估整体框架

从10 kV线路和配电网系统两个层面，选择电压合格指标、电压偏差指标和线路重载指标对系统运行状态进行评估。基本概率评估指标经过特征加权得到10 kV线路层与配电网层的单项评估指标，再通过熵权法得到整体概率评估指标。各部分的具体结构如图2所示。

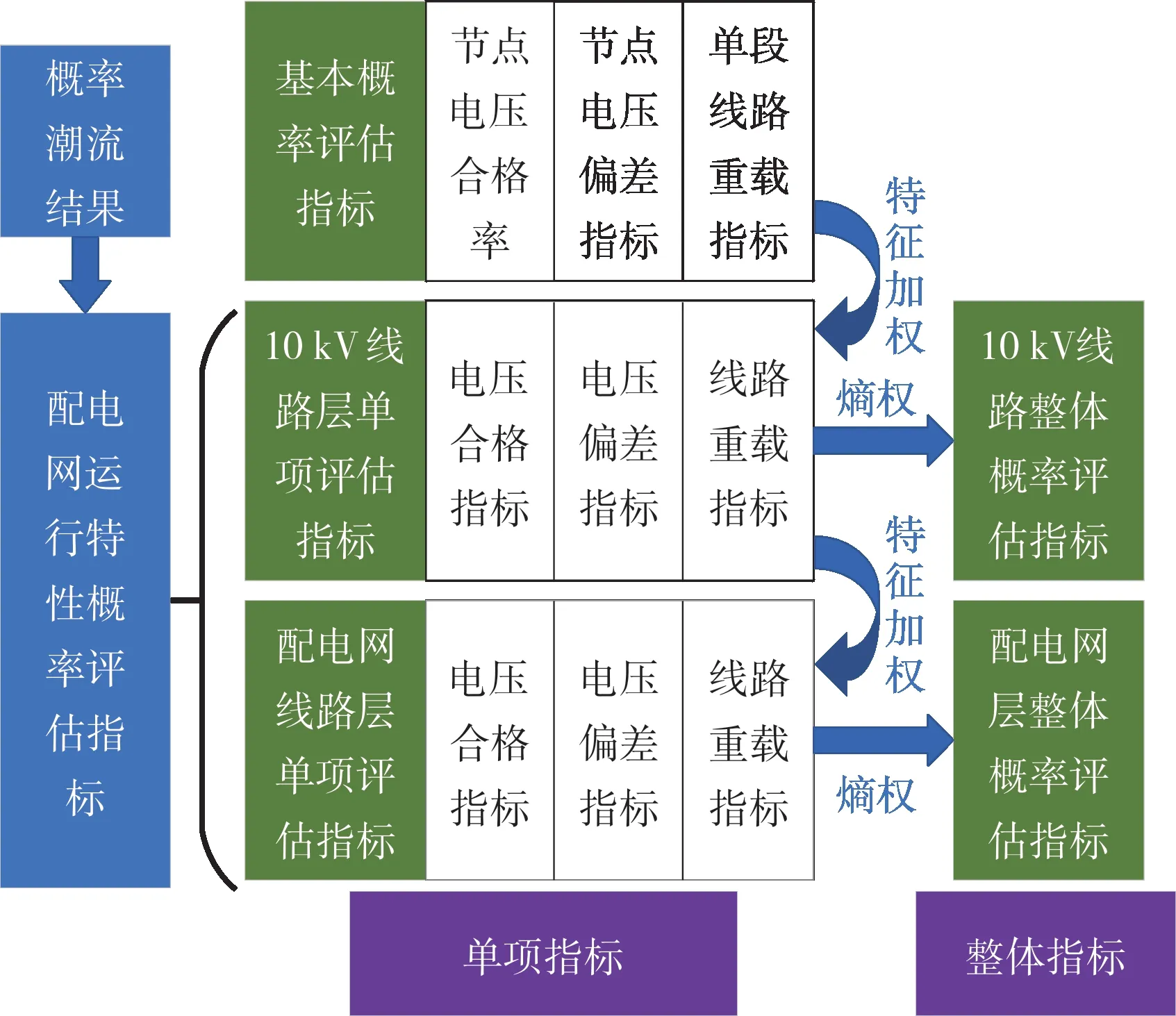
图2 配电网概率指标评估方法结构

2.2 基本概率评估指标

2.2.1 节点电压合格率

节点电压合格率表示配电网特定节点在特定时刻的电压幅值概率分布的量化，以节点j为例，在t时刻其节点电压合格率指标RNU，jt计算方法如式（5）所示：

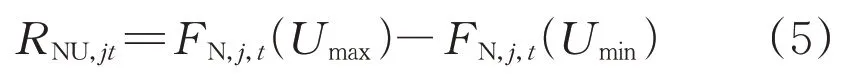
式中：FN，j，t(·) 表示节点j在t时刻电压幅值的累积概率分布函数；Umax和Umin分别表示电压合格的上限和下限，分别取1.07 p.u.和0.93 p.u.［19］。

2.2.2 节点电压偏差指标

节点电压偏差指标表示该节点电压与线路根节点电压的差值，包括最低电压、最高电压差值，具体计算式如式（6）所示：

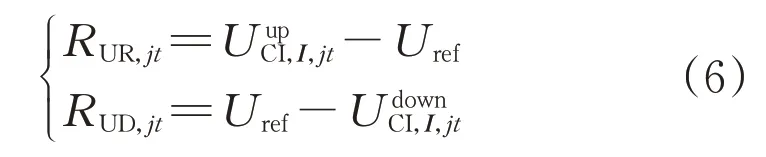
式中：RUR，jt和RUD，jt分别表示节点j在t时刻的电压抬升偏差指标和电压降落偏差指标；和分别表示t时刻节点j的电压在该节点概率分布置信区间I的上界和下界；Uref表示10 kV 线路根节点电压幅值。

2.2.3 单段线路重载指标

单段线路重载指标计算方法如式（7）所示：

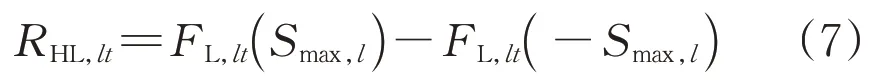
式中：FL，lt(·)表示线路段l在t时刻的视在功率累积概率分布函数；Smax，l表示线路的重载功率标准，一般采用线路最大载流量的80%。

2.3 10 kV线路层运行特性概率指标

为避免10 kV线路在概率指标分析时，大量正常运行状态的数据将电压越限、线路过载等问题数据淹没，采用特征加权法有效反映配电网的运行问题。其权重结构如图3所示。

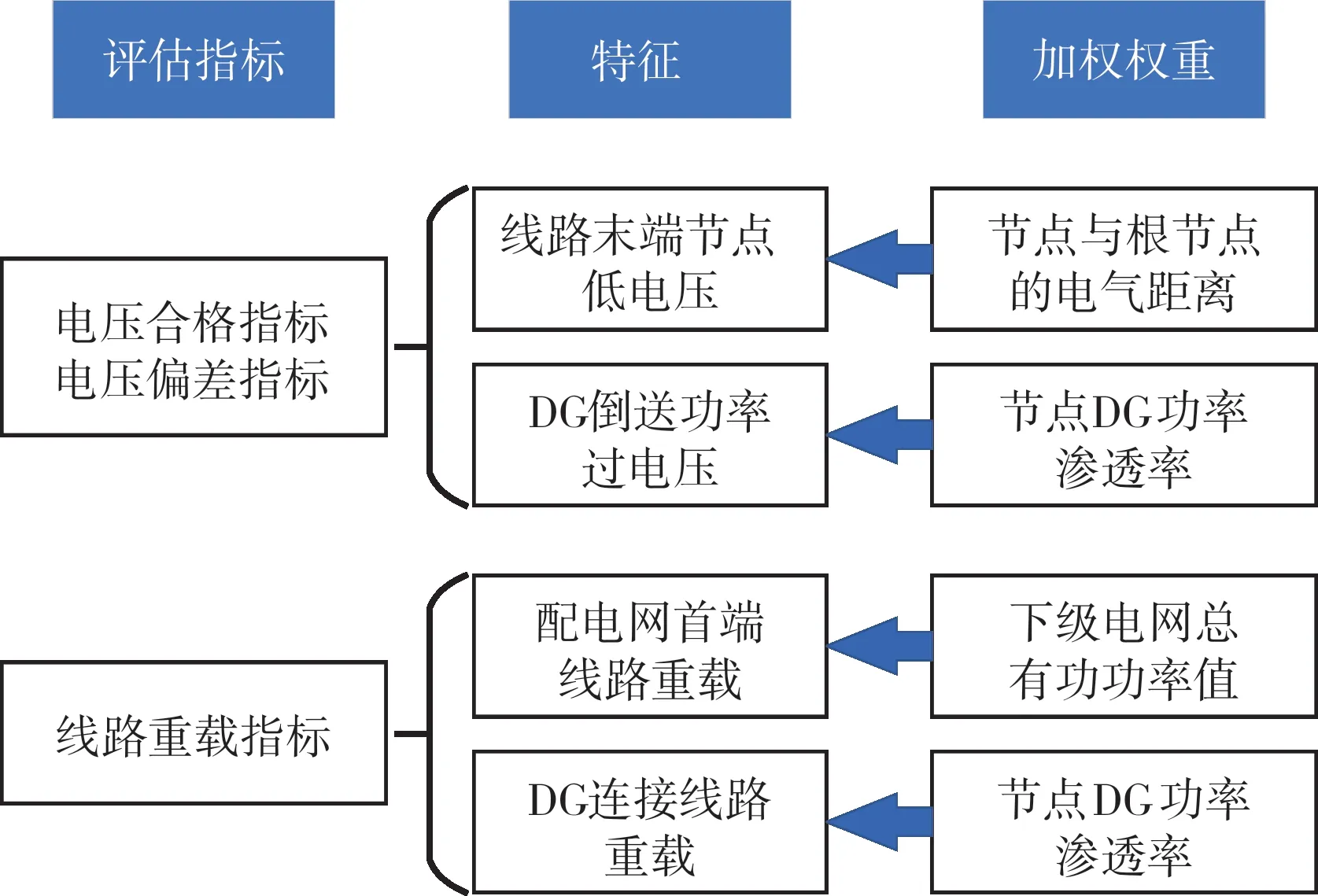
图3 10 kV线路单项评估指标权重选取结构图

2.3.1 10 kV线路单项评估指标

1）10 kV线路电压合格指标

由于节点电压越限情况与该节点的注入功率和整条10 kV线路的负荷大小及分布位置均密切相关，因此选取电压越限节点与线路根节点的电气距离和节点分布式电源的功率渗透率作为特征权重。

电气距离的特征权重通过节点到10 kV线路根节点（上级变电站10 kV电压母线）的阻抗确定，具体计算如式（8）所示：

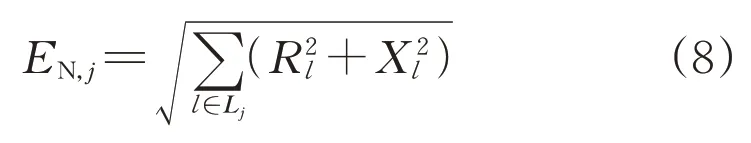
式中：EN，j表示节点j到10 kV 首端节点的电气距离；Rl和Xl分别表示支路l的电阻与电抗；Lj表示在辐射状网络中节点j到根节点最短联通线之间的所有线路段集合。

由于只有节点分布式电源功率渗透率大于1时才可能导致过电压，因此分布式发电权重在功率渗透率小于1时不应当赋予过电压的权重，具体计算如式（9）所示：

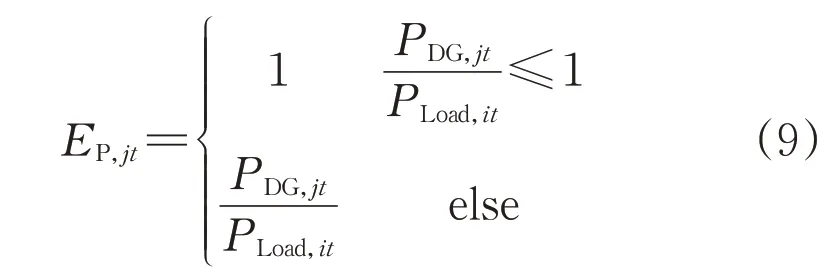
式中：EP，jt为中间变量，表示节点j的倒送功率水平，无倒送功率时取1；PDG，jt和PLoad，it分别表示节点j分布式电源的输出功率和负荷功率。

t时刻节点j电压合格率的权重系数ωUR，jt计算如式（10）所示：

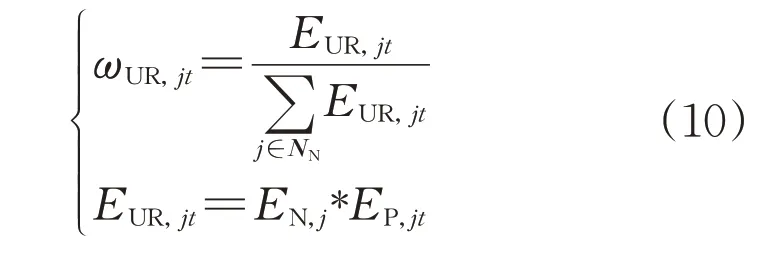
式中：EUR，jt为权重归一化之前的中间变量；NN表示10 kV线路的负荷节点集合。

10 kV 线路整体电压合格指标计算方法如式（11）所示：

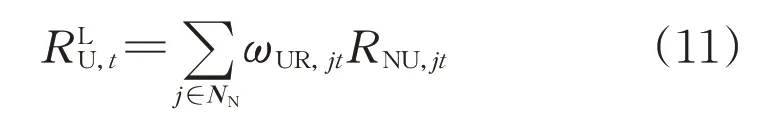
式中：上标L表示评估对象为线路。

2）10 kV线路电压偏差指标

10 kV线路电压偏差指标用于对置信区间Ⅰ内的线路整体电压质量进行评估，计算中采用与电压合格指标同样的权重进行特征加权，其评估指标可表示为：

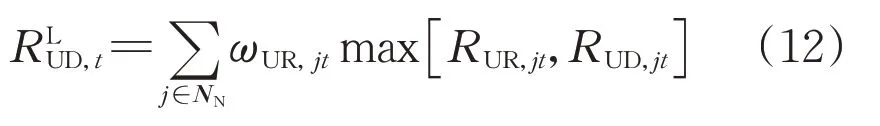
3）10 kV配电线路重载指标

配电网通常为辐射状拓扑结构，其重载线路主要出现在两种类型的线路段上：辐射状网络的首端线路段；具有较大倒送功率的负荷节点所连接的支路。对以上两类线路进行特征加权，得到权重如式（13）所示：

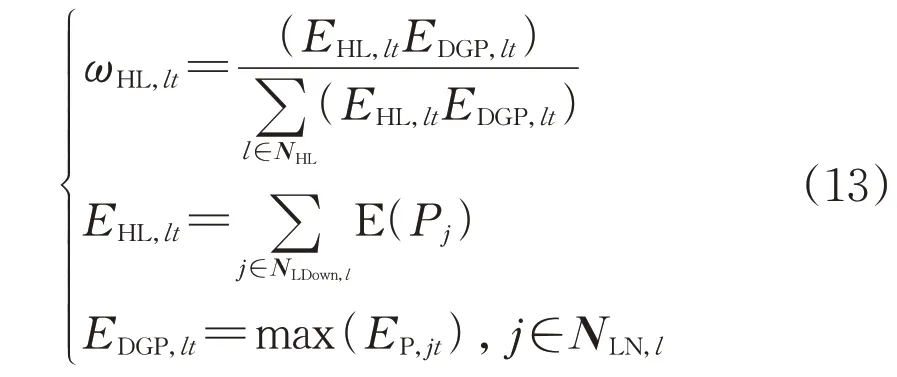
式中：ωHL，lt表示在计算10 kV 配电线路重载指标时线路l在t时刻的权重；E(·)为期望值运算；EHL，lt为中间过程变量，表示线路l的下级网络中所有负荷点功率的期望值之和；EDGP，lt表示用于反映线路l两端节点功率渗透率水平；NLN，l表示线路l两端节点的集合；NLDown，l表示线路l的下级网络节点集合。

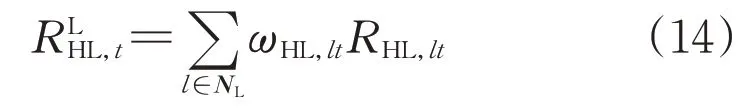
式中：NL表示10 kV 线路中包含的所有线路段的集合。

2.3.2 10 kV线路整体评估指标

对1条10 kV线路进行综合评估时，需要综合考虑10 kV线路电压合格指标、电压偏差指标、重载指标三方面的影响，通过对以上三项指标进行加权得到10 kV配电线路整体特性的评估指标。熵权法通过物理信息熵进行权重分配，将不同指标的信息熵水平作为指标的权重系数。它将对系统状态变化灵敏度更高的指标赋予更高的权重，进一步放大不同状态之间的差异，因此，非正常运行状态将被赋予更高的权重。熵权法的权重确定方法计算步骤如下：

1）评估指标标准化

为了在同一个计算尺度中评估各项指标物理信息熵，需要对原有指标计算值进行标准化处理。10 kV线路电压合格指标为正向指标，即指标值越大评价越正面；10 kV线路电压偏差指标、线路重载指标为负相关指标，表示指标值越大评价越负面。在评估指标标准化中，正向指标和负向指标的极差化方法如式（15）所示：

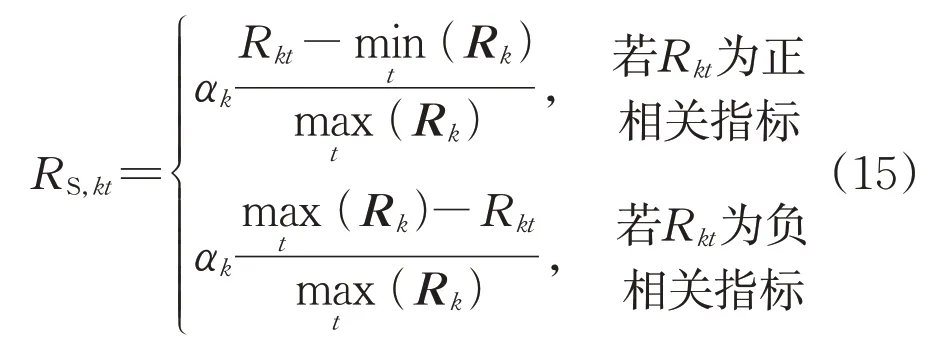
式中：RS，kt表示指标k在t时刻标准化后的评估指标；Rkt表示标准化前的t时刻评估指标k；Rk表示指标k在不同时段取值的集合；αk表示指标k的系数。

2）物理信息熵

选择一天中不同时段作为熵权法的场景，进行运行指标的物理信息熵计算，如式（16）所示：

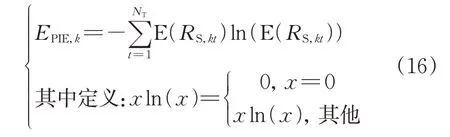
式中：EPIE，k表示指标k的物理信息熵；NT表示一天中分析的时段数量。

3）熵权法的权重计算

对不同指标的物理信息熵进行标准化处理，以满足全概率公式约束，如式（17）所示：

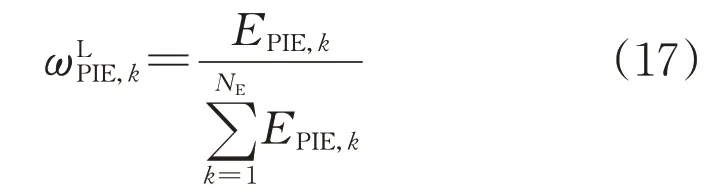
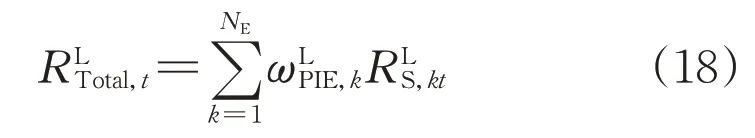
2.4 配电网整体运行特性概率指标

2.4.1 配电网整体线路单项评估指标

在对一个配电网进行整体指标评估时，需要综合考虑多条10 kV线路的指标，确定不同线路在指标中的权重。在评估不同指标时需要考虑到不同评估对象的差异，针对性地配置权重。

电压指标方面，10 kV线路电压合格指标、电压偏差指标均是对10 kV线路节点电压的评估，因此采用10 kV线路的节点数量作为不同10 kV线路电压指标的特征权重，如式（19）所示：

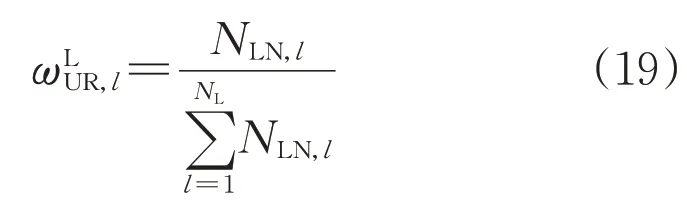
线路重载指标方面，10 kV线路重载指标主要用于反映线路整体的负荷情况，因此采用线路有功功率总负荷作为权重，如式（20）所示：

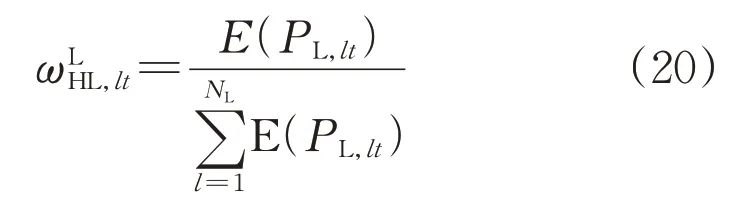
通过特征加权方法对各10 kV线路单项评估指标加权，得到配电网的各项指标如式（21）所示：

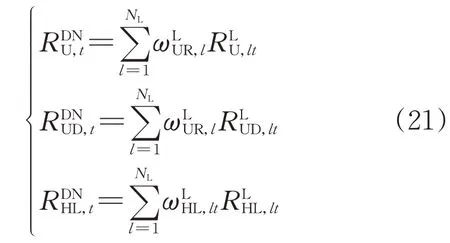
2.4.2 配电网整体线路整体评估指标

配电网的整体指标计算如式（22）所示：

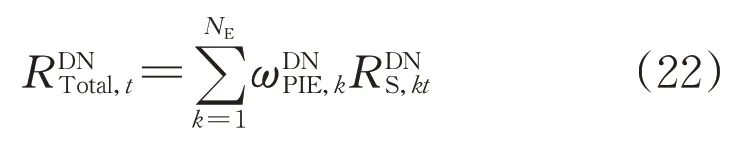
3 案例分析

3.1 案例基本情况

对我国华东地区某城市某区实际案例进行分析，该地区的核心段主要由2 条10 kV 线路供电，分别来自2个不同的110 kV变电站：其中，10 kV线路1主干线路长4.3 km，供电区域主要为工商业区；10 kV线路2主干线路长2.5 km，供电区域类型主要为居民区与其他类型区域。

以线路1为例，进行案例分析。线路1的接线示意图如图4所示。图中蓝色部分为居民区，黄色部分为工商业区（主要以生产单位、企事业单位等为主），红色部分代表其他类型区域，编号为电气节点序号，其中节点1为线路1的根节点。

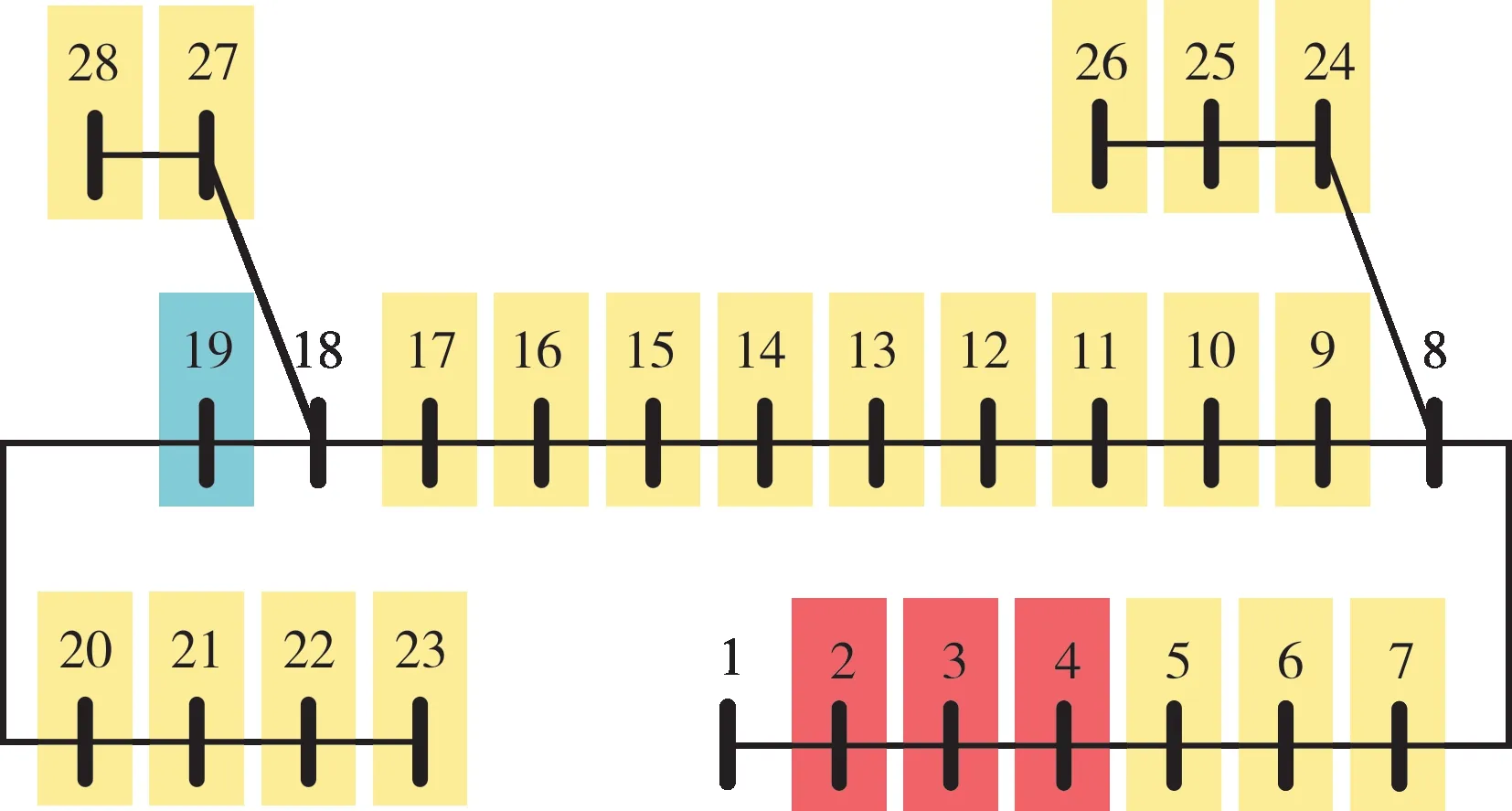
图4 案例地区线路1接线示意

3.2 电动汽车接入前后的概率潮流结果

3.2.1 电动汽车接入前线路概率潮流结果

在统计线路1 上所有负荷节点在2019 年全年8 760 h 的负荷后，获得线路上所有负荷节点的有功功率、无功功率分布情况。10 kV线路1总视在功率的95%置信区间如图5所示。线路1负荷主要集中在日间工作时间段，从17：00 开始略有下降，在00：00后明显下降。

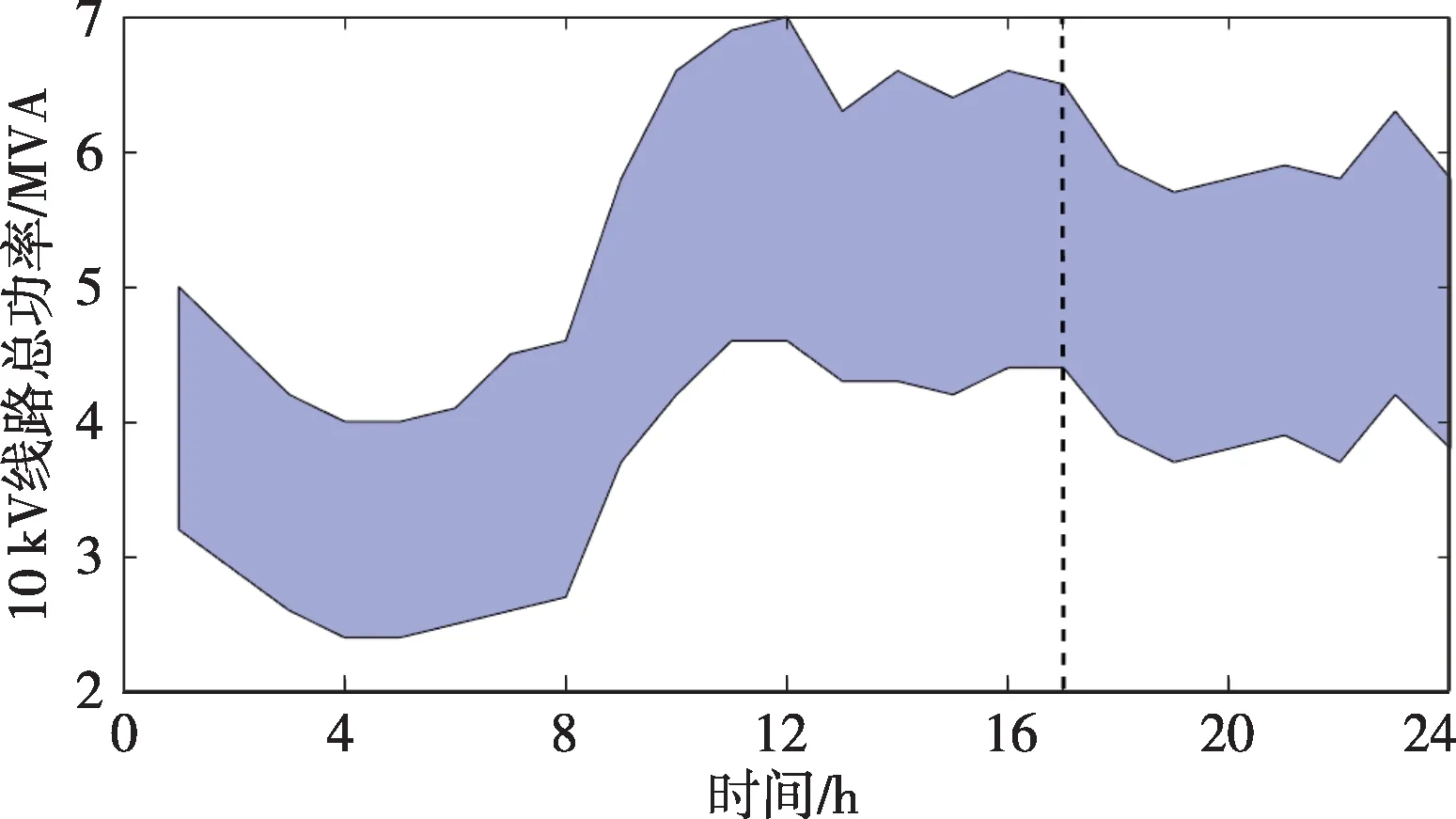
图5 10 kV线路1总功率95%置信区间分布

3.2.2 电动汽车接入后线路概率潮流结果

本案例考虑5种不同电池容量和充耗电特性的电动汽车，具体参数如表2所示，车辆充满时电池SOC（荷电状态）为95%。

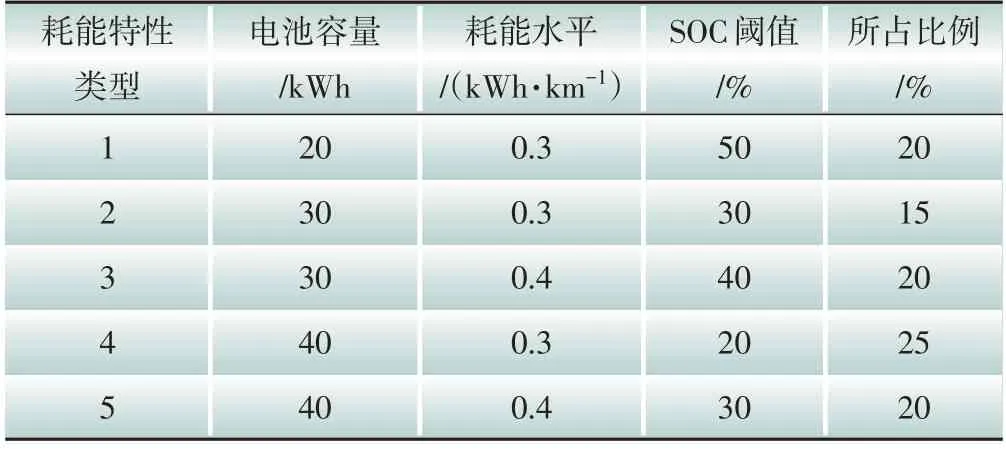
表2 不同耗能特性车辆参数

案例中进一步将车辆类型分为私家车与出租车，并根据实际情况中私家车和出租车的数量，设置二者的比例为19：1，相关充电特性建模参见文献［20］；电动汽车的单车充电功率在工商业区和其他区域为60 kW，在居民区为7 kW；采用2种不同的充电模式，分析电动汽车接入数量的差异对配电网运行状态的影响，具体参数如表3所示。

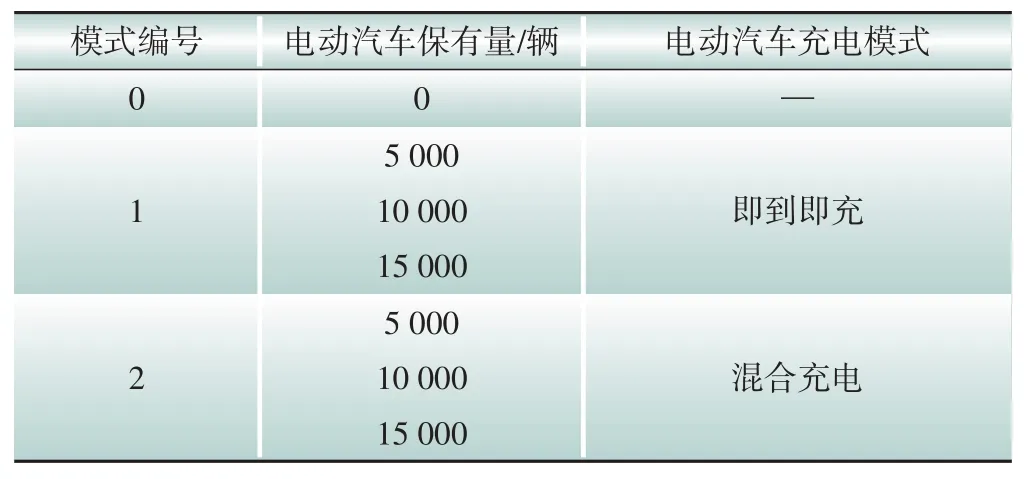
表3 充电模式信息

表3中，电动汽车的即到即充模式是指在车辆抵达目的地后即开始充电，直至充满；混合充电模式指在车辆正常抵达目的地后根据SOC 决定是否充电［21］，仅在SOC低于阈值才充电并充满，结束一天最后一次出行后采用即到即充模式。由于即到即充模式在电动汽车每到达一处目的地后均立即开始充电，势必引起充电负荷突增；混合充电模式在尚未结束一天的最后一次出行前，充电负荷增加程度低于即到即充模式。

电动汽车不同的充电模式对配电网的整体影响不同，以充电模式1和2为例（保有量为15 000），两种充电模式下10 kV 配电线路1 的总视在功率95%置信区间分布情况如图6所示。

图6中红色部分表征电动汽车对配电网产生的影响。结果表明，电动汽车充电功率主要分布时段与工作时段一致。即到即充模式的车辆充电负荷分布在全天的各个时段内；混合充电模式的车辆在夜班抵达工商业区或回到居民区后开始充电，因此主要集中在一天中的后半时间段。

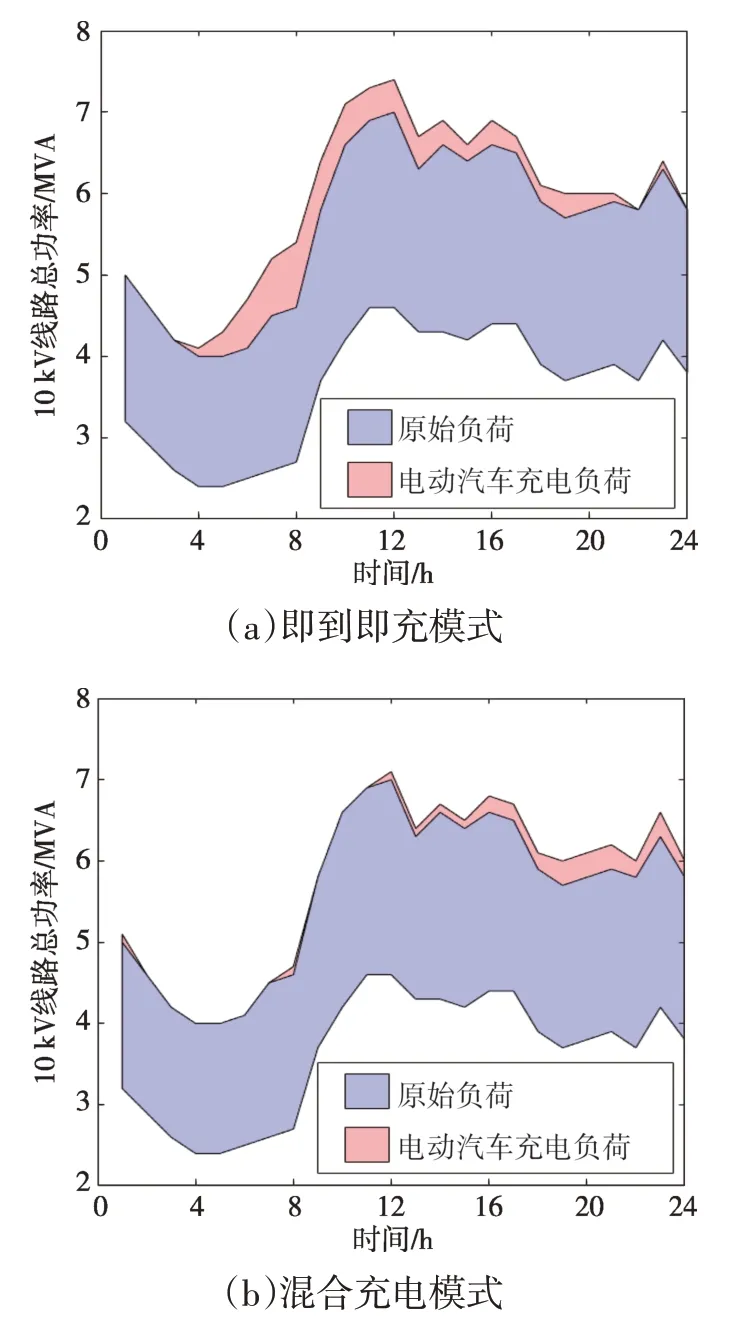
图6 10 kV线路1总视在功率95%置信区间分布

3.3 电动汽车接入前后配电网运行概率指标评估

3.3.1 电动汽车接入前配电网运行概率指标

10 kV线路1的基本概率指标和指标计算结果分别如图7 和图8 所示。当不考虑电动汽车接入时，线路1无电压越限问题，10 kV线路电压合格指标取值为1；电压降落95%置信区间内最大压降偏移相对较小；线路1 在节点1—节点5 之间的线路段存在一定的重载风险，其中节点1和节点2之间的线路段1在12：00有2.386%的概率重载。

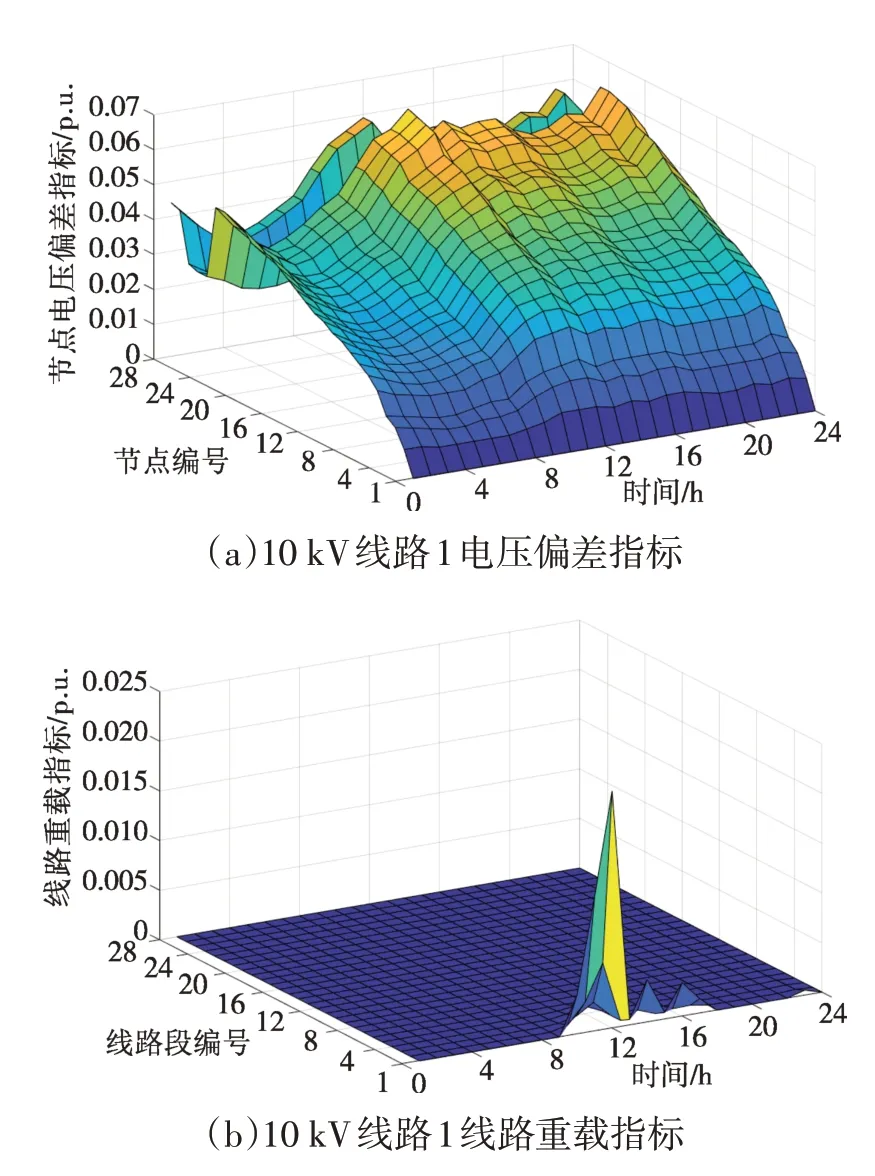
图7 10 kV线路1基本概率指标

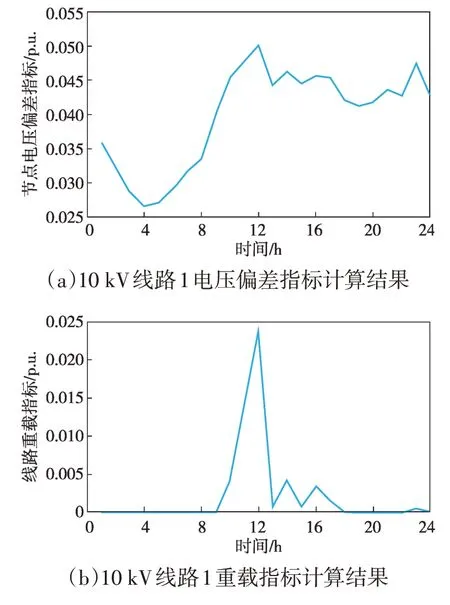
图8 10 kV线路1现状评估指标

3.3.2 电动汽车接入后配电网运行概率指标

1）10 kV线路电压合格指标

由于线路负荷相对较小且供电半径有限，无明显低电压现象；线路上级变电站10 kV母线电压较高，且线路无倒送功率负荷节点，因此也不存在过电压现象。线路1在不同充电模式下均未出现电压越限问题。

2）10 kV线路电压偏差指标

10 kV 线路1 电压偏差指标计算结果如图9 所示，其中充电模式中括号内数值表示电动汽车保有量。电压偏差指标在不同的充电模式下差别较小，指标较大的时段主要集中在10：00—12：00，对应图6中负荷水平较高的时段，此时线路电压偏差指标超过0.05 p.u.。

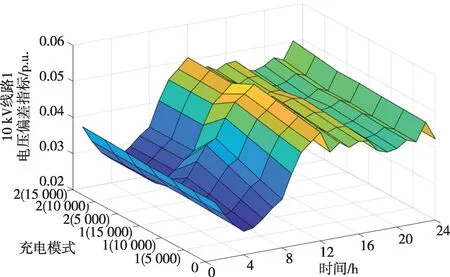
图9 10 kV线路1电压偏差指标变化情况

3）10 kV线路重载指标

10 kV 线路1 重载指标计算结果如图10 所示。线路过载时段主要集中在10：00—12：00，即到即充模式对该指标的影响较大，且电动汽车保有量的增加会进一步恶化线路重载指标：当电动汽车保有量为15 000 时，12：00 的重载指标为0.148 5，较无电动汽车接入时的峰值0.023 9 增大了521.3%；与即到即充模式相比，混合充电模式下电动汽车保有量对指标的影响较小，电动汽车保有量为15 000 时的线路重载指标比电动汽车保有量为5 000时仅增加30.84%。

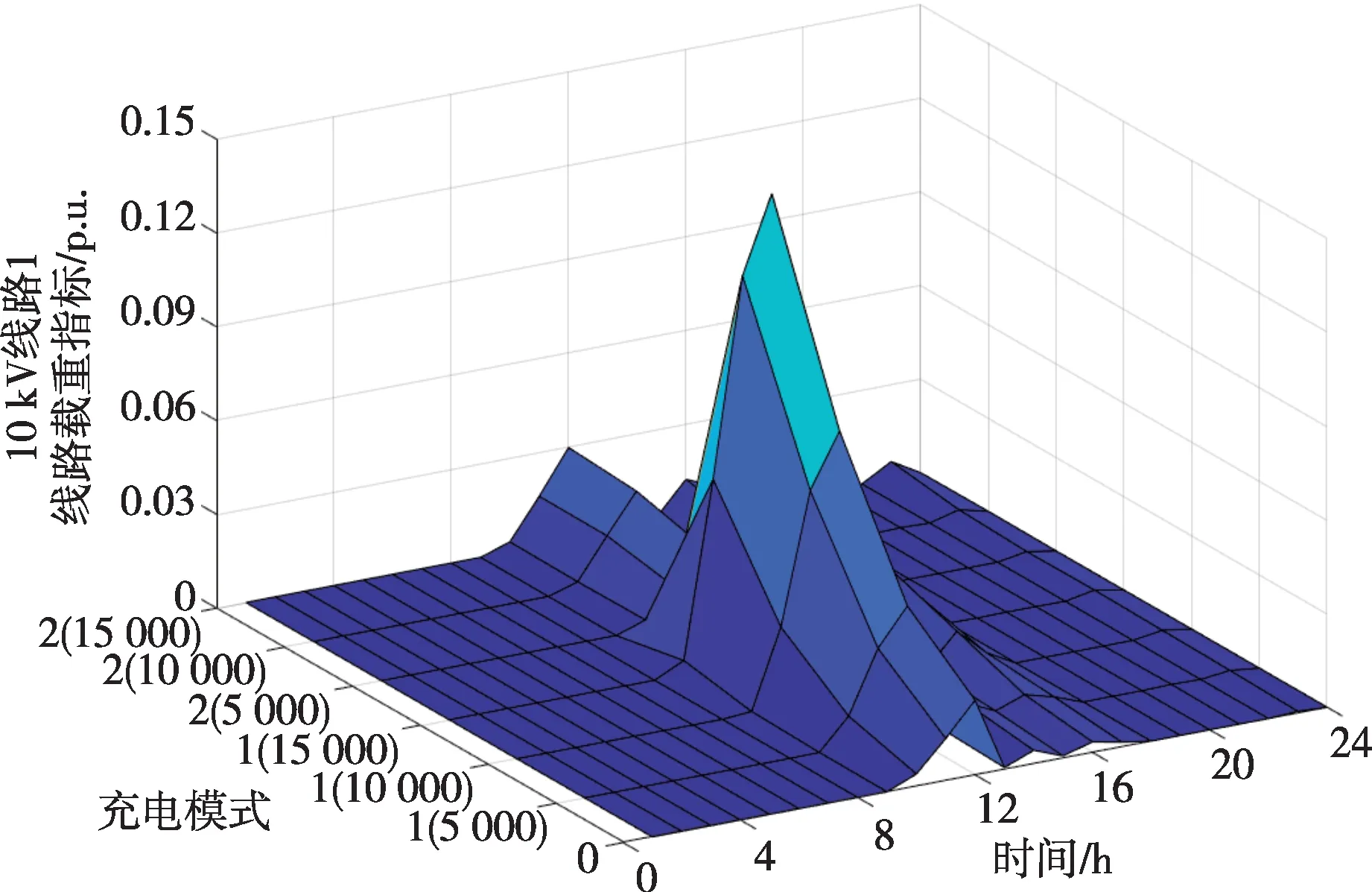
图10 10 kV线路1线路重载指标变化情况

4）10 kV线路整体概率评估指标

10 kV线路1整体指标在不同充电模式下的计算结果如图11 所示。凌晨至夜间时段，不同的充电模式下指标差异较小；午间即到即充模式相对于混合充电模式出现了更明显的指标下降，表明即到即充模式下电动汽车充电负荷会显著影响线路整体指标，其影响也会随着电动汽车保有量的增大而加剧。

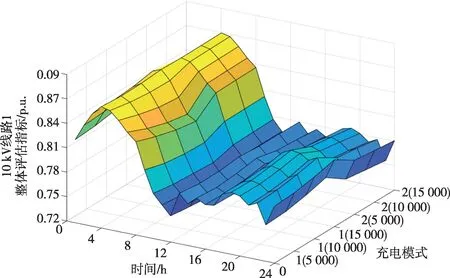
图11 10 kV线路1线路整体指标

3.4 案例对比

传统评估方法和本文方法的指标对比结果如表4 所示。从表4 中可以看出，与传统方法相比，本文所提方法得到的电压偏差指标值和线路重载指标值显著增大，能够更有效地反映电动汽车大量接入后线路存在的电压偏差过大、线路过载等风险。此外，随着电动汽车保有量的增加，线路电压偏差指标和线路重载指标峰值都大幅增高。

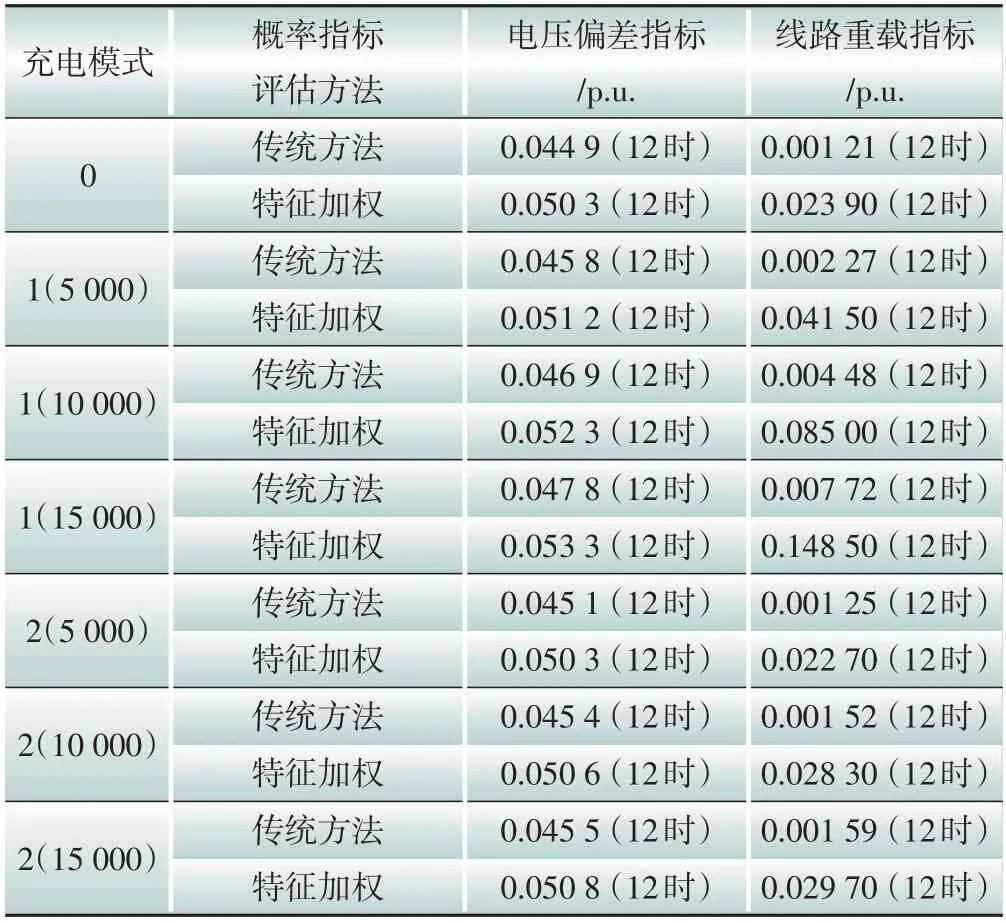
表4 传统方法与本文方法的对比

4 结论

本文围绕电动汽车接入对配电网运行特性各项指标的影响进行了量化分析，得到结论如下：

1）对电动汽车接入前后的配电网潮流进行概率潮流计算，能够使配电网运行特性的各项概率评估指标得到全面准确的反映。

2）以概率潮流的计算结果为基础，提出了基于特征加权的配电网运行特性概率指标评估方法，从10 kV线路层和配电网整体两个层面评估了配电网运行中节点电压越限情况、电压偏差水平和线路重载水平。选取一处实际电网案例进行分析，结果表明，特征加权方法提高了评估指标反映运行问题的有效性，并通过熵权法降低了人为主观因素的影响，有助于解决电动汽车接入后配电网的不正常运行状态不能得到准确有效反映的问题。