加工监控数据准确性量化评价及优化研究
2022-04-04唐思游胡小锋刘颖超
唐思游,胡小锋,刘颖超
(上海交通大学 机械与动力工程学院,上海 200240)
0 引言
加工监控数据被广泛应用于数据分析,依其结果做出的决策对产品质量、成本控制、生产效率影响巨大。因此,符合标准的数据质量是数据分析结果有效的先决条件。监控数据无法获取理论真值,难以对数据准确性进行量化评价,而定量的准确性评价是精准优化的基础,从保证数据质量出发,进而保证数据分析的准确性和有效性。
近年来,国内外许多学者致力于数据准确性的研究。武荣坤[1]提出趋势预测法和回归预测法分析统计数据可靠度;戚桂杰等[2]提出回归分析法检测污染数据和异常点;王华等[3]提出了逻辑规则检验、经验参数对比、相关指标变动趋势比对法;史晓贞等[4]针对桥梁健康监测系统数据准确性分析提出了位置对比法和相关性分析法;NRMAN等[5]提出概率关系模型,用于业务流程中的数据准确性评估;GARCIA等[6]提出贝叶斯序列概率推断法来提高动态测量数据的准确性;李勇[7]提出基于差分的分位数可疑数据检测方法;成邦文等[8-9]提出了统计分布检验与基于统计分布的异常数值识别方法;RAMASWAMY等[10]提出循环嵌套、基于索引和划分算法对数据集中的异常值进行识别;刘波等[11]等从规则度量关系及其相关分析的角度对数据准确性进评估与优化;张福民等[12]基于蒙特卡洛仿真方法从测量不确定度角度对多仪器融合测量结果准确性进行评价。上述研究主要面向统计数据及实验室环境下的数据准确性评价和异常数据识别,尚未有相关文献针对实际加工现场的监控数据进行数据准确性的量化评价。
数据准确性对数据分析效果影响方面,OSEI-BRYSON等[13]综述了使用数据挖掘结果来支持决策时数据信息正确且准确的必要性以及劣质数据对于数据挖掘项目的影响;STANG等[14]面向工单数据系统,删除低质数据后进行工单延迟预测以验证数据准确性的重要性;BLAKE等[15]以J48分类算法为对象研究了数据准确性、完整性、一致性、时效性以及问题复杂度对数据分析效果的影响。然而,上述研究不针对实际加工监控数据准确性对数据分析效果的影响,且数据优化过程改变了数据集大小。
本文提出一种基于测量不确定度的数据准确性量化评价方法,该方法可以针对无理论真值的加工监控数据进行准确性量化评价。通过欧氏距离下局部敏感哈希技术(Locally Sensitive Hashing under Euclidean2, E2LSH)及k邻近优化算法(k-Nearest Neighbor, kNN)对数据准确性进行针对性的优化。最终将优化前后的数据用于基于相似性的铣刀剩余寿命预测,以验证数据准确性进行量化评价及优化的重要性和有效性。
1 监控数据准确性的量化计算及评价框架
1.1 基于测量不确定度的数据准确性计算
在GB/T 25000.12—2017中对数据准确性定义为:特定使用周境中,数据具有准确表示一个概念或事件相关属性真实值的属性的程度[16]。监控数据无法获取理论真值从而无法定量计算数据准确性。测量不确定度表征被测量估计值的分散性,其值越小,数据质量越高,使用价值越大[17]。因此,本文构建测量不确定度法与数据准确性建立联系,实现监控数据准确性的量化评价,量化评价步骤如图1所示。
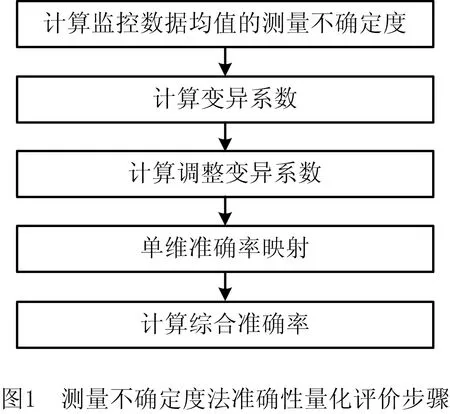

(1)

表1 测量数据样表
为消除数据的测量尺度与量纲影响,引入变异系数vpq:
(2)

(3)
式中r为调整比例,依据实际vpq分布而定。
(4)
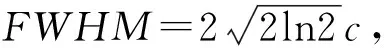
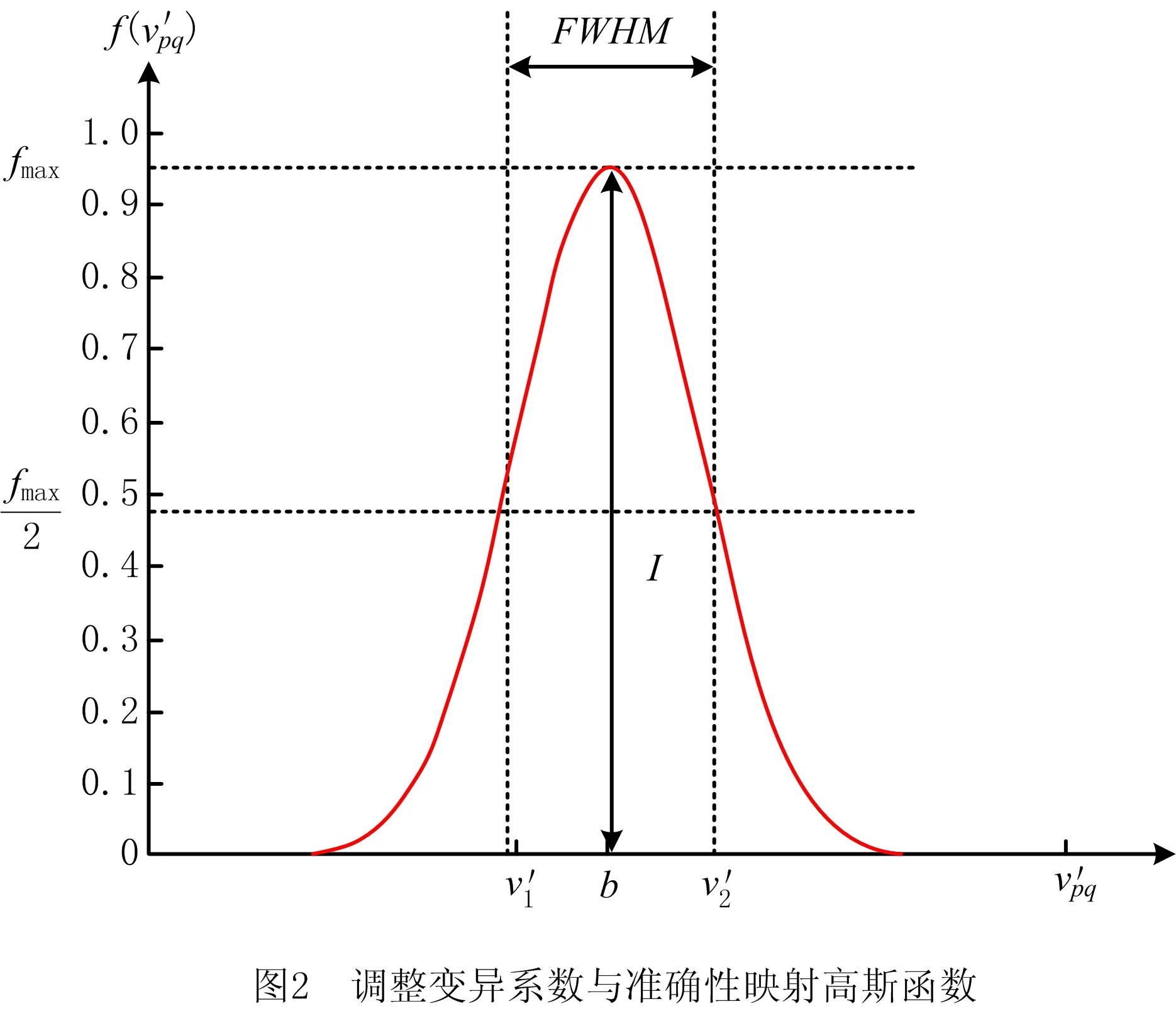
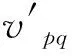

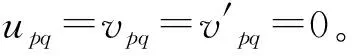
建立准确性映射得到apq后,当数据属性A1,A2,…,Aj分别对应权重ω1,ω2,…,ωj(赋权法详见1.2节),则某条数据记录的准确性为:
(5)
1.2 数据属性赋权
赋权法包括主观赋权法和客观赋权法。主观赋权法包括层次分析法、专家咨询法、二项系数法等;客观赋权法包括变异系数法、熵值法、灰色关联度法等[19]。层次分析法通过将复杂评价问题逐级拆解,使其具有可操作性,决策者可根据历史经验和当前问题动态调整属性重要度,实现定性与定量分析相结合;变异系数法能客观体现各数据属性的内在差异及特征,计算方法简单高效。为准确客观地赋权,同时考虑主观经验与样本数据特征,本文选择将层次分析法与变异系数法赋权结果平均,得到最终权重。
层次分析法将复杂问题分解为若干个有序的递阶子层级,在每层内部请该领域专家将数据属性两两对比,构建判断矩阵。本文借助皮尔逊相关系数、动态层次聚类的关键因素挖掘[20]来构建判断矩阵。以表1为例,属性Ap与Aq重要性比较结果为dpq,则判断矩阵
(6)
判断矩阵标度标准如表2所示。

表2 判断矩阵标度标准
将D中元素按列归一化:
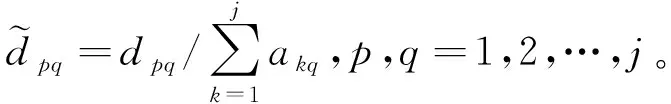
(7)
将归一化后的矩阵的同一行的各列相加:
(8)
将相加后的向量除以j即得权重向量:
(9)
计算最大特征根:
(10)
判断矩阵D的一致性检验指标(C.I.):
(11)
引入一致性比例(C.R.):
(12)
其中R.I.为随机一致性指标,如表3所示。

表3 平均随机一致性指标R.I.
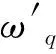
变异系数法基本思想是:在评价体系中,数据取值差异越大的属性越能反映被评价单位的差距。为消除各数据属性量纲不同产生的影响,引入权重变异系数:
(13)
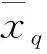
各项指标权重为:
(14)
综合层次分析法与变异系数法,最终权重为:
(15)
2 监控数据准确性优化
数据准确性优化依赖于数据清洗,即通过检测和消除实例级数据质量问题提高数据质量[21]。数据优化应综合考虑优化效果及效率,kNN精度高但计算复杂度高、数据集较大时优化效率低。E2LSH适用于在海量高维数据中搜寻近似项,可弥补kNN的低执行效率。本文将E2LSH及kNN结合,以实现高效、高精度数据准确性优化[23]。
优化思路为:监控数据集为T,经过数据准确性计算后选出待优化数据集Q及无需优化数据集V,通过E2LSH方法将数据v(v∈V)进行映射,建立哈希表,数据q(q∈Q)进行E2LSH映射后进行哈希表查询,找出k个与q最临近的点进行kNN优化。
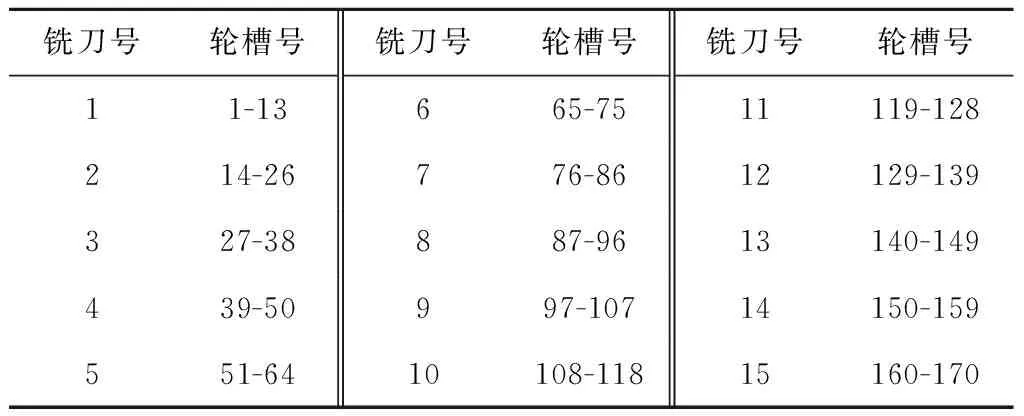
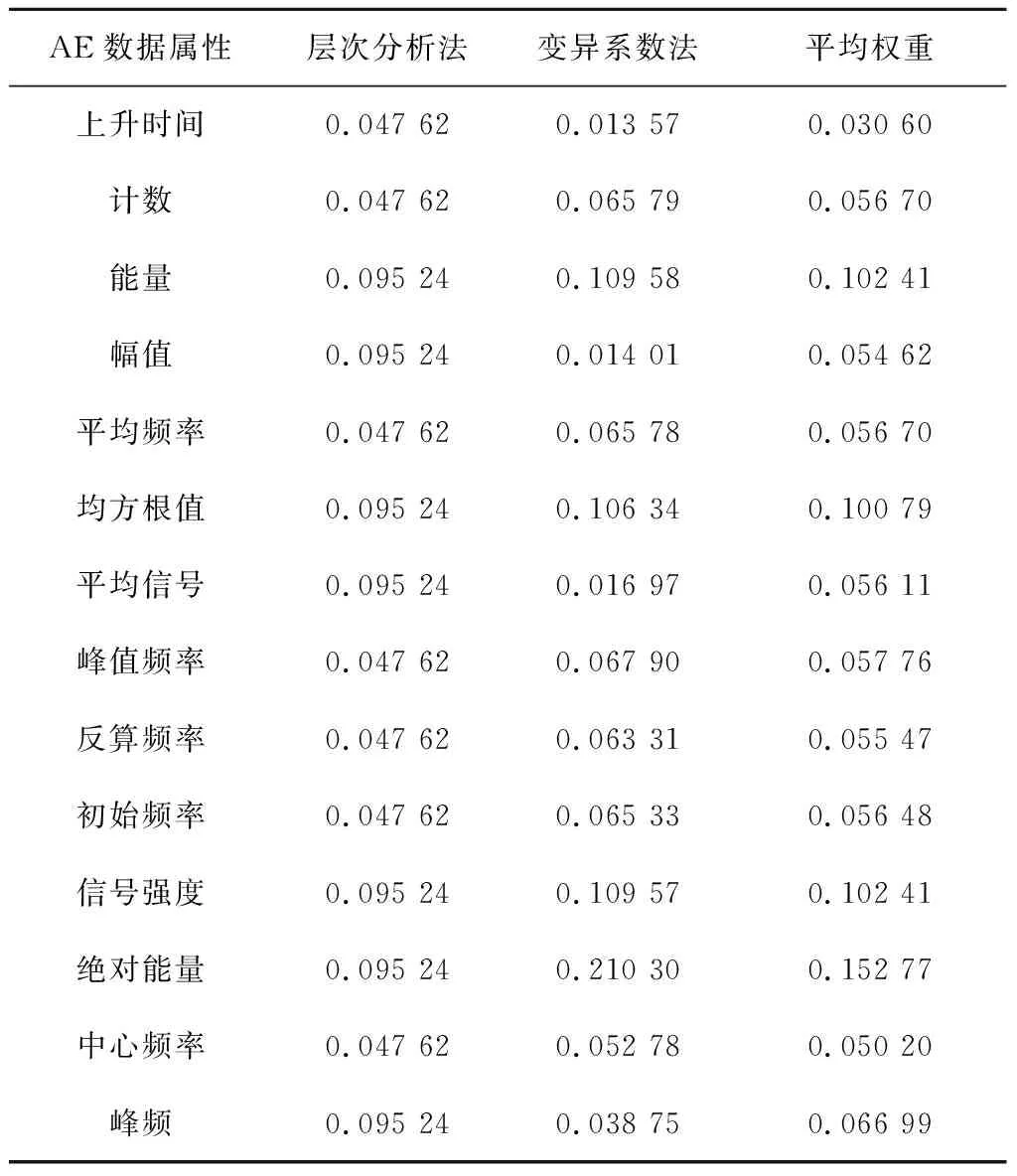
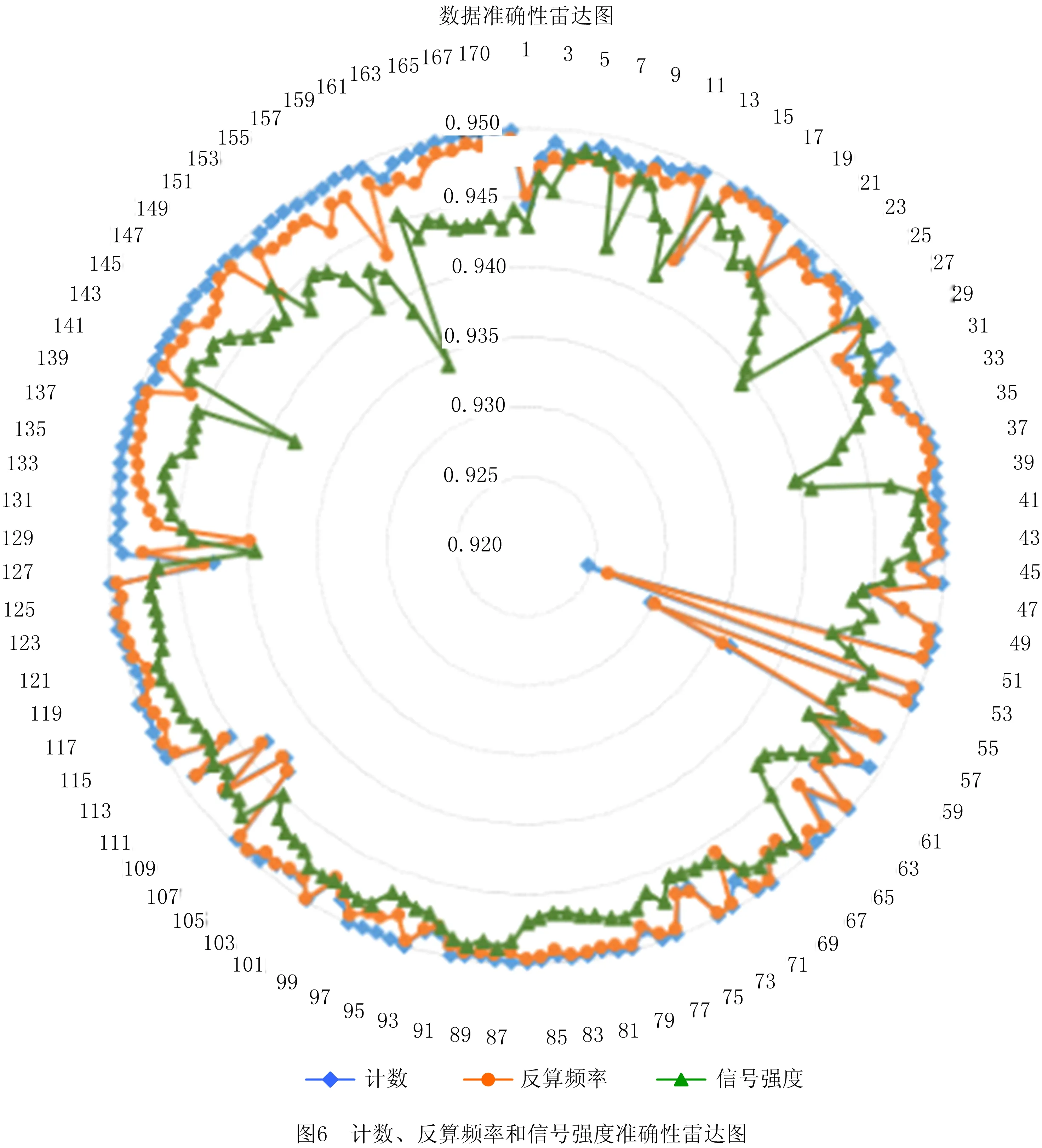
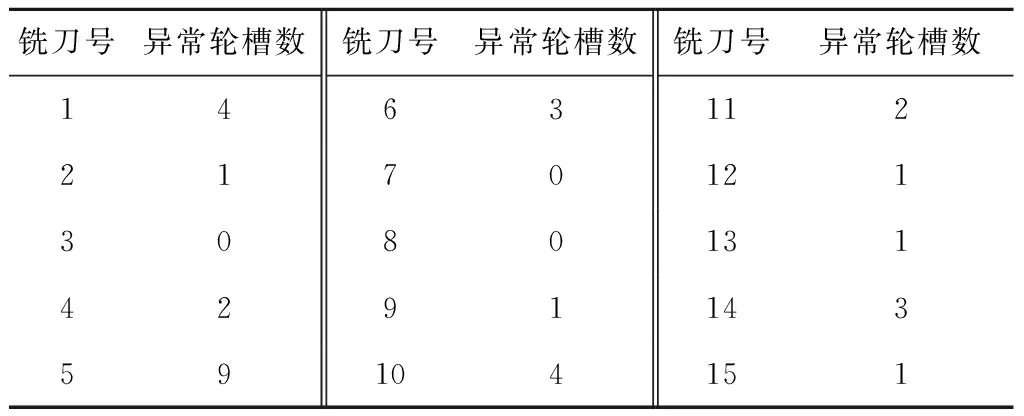
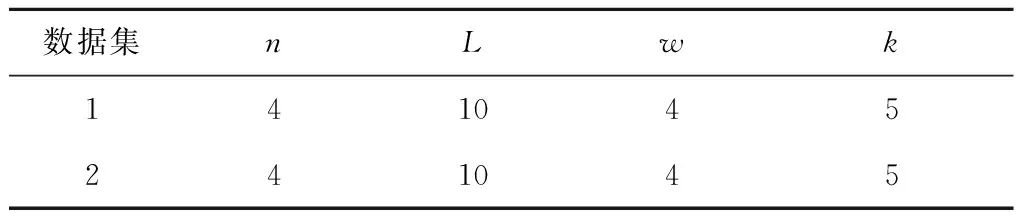
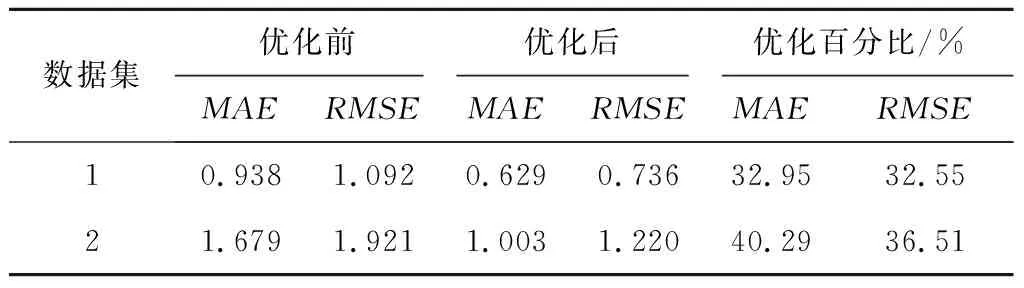
E2LSH基本思想:将原始特征空间中相邻的两个数据点通过相同的投影或者变换后,这两个点具有较大概率仍然相邻,原始特征空间中不相邻的点具有较大概率仍不相邻[25],即H={h:S→U},H是局部敏感的:对于任何v,q∈S,若v∈B(q,r1)则PrH[h(q)=h(v)]≥p1,若v∉B(q,r2)则PrH[h(q)=h(v)]≤p2。其中:B(q,r)={v∈S|D(v,q)≤r};PrH为概率;p1>p2;r1 上述h为哈希函数:ha,b(v):Rd→N为映射一个d维特征向量v到一个整数集, (16) 式中:a为一个d维特征向量,每一维是一个独立选取的满足P稳定分布的随机变量;b为[0,w]范围内的一个随机数;w表示当a.v将高维向量映射到实轴后,将实轴以宽度w等分,并对每段区域从左至右标号,将a.v映射后所在的区域标号作为其哈希取值。w实际取值取决于数据集Q及V,一般取w=4[23]。 定义一个函数族G={g:S→Un},选取n个哈希函数hi∈H组成g(v)=(h1(v),…,hn(v));取整数L,从G中选取L个函数g1,…,gL;另外定义两个哈希函数H1和H2,H1值作为哈希表索引,H2值作为链表中的关键值。具体形式如下: (17) (18) 其中:ri,li是随机整数;tablesize为哈希表长度;C为一个大的素数,由计算机位数决定,例如32位机器取C=232-5,C的取值大小以满足哈希函数进行高效计算而无需使用模运算为目标[23]。 kNN中选取与待优化点q距离最近的前k个点v1,…,vk,q的第i个维度的优化值为: (19) 其中Dij为第i项与第j项的距离,本文取欧氏距离。 E2LSH_kNN算法步骤如图4所示。 本文实验平台由某汽轮机厂提供,采用15把J1型轮槽铣刀对汽轮机转子轮槽进行精铣削加工。采用PCI-2AE采集声发射(Acoustic Emission, AE)信号,采样频率为1 MHz。加工现场如图5所示。 样本数据集包含由15把精铣刀加工的共计170条轮槽的监控数据,每条轮槽持续监控得到10 000条数据记录,每条数据记录包含14种AE属性:上升时间、计数、能量、幅值、平均频率、均方根值、平均信号电平,峰值频率、反算频率、初始频率、信号强度、绝对能量、中心频率、峰频。将每条轮槽的10 000条AE数据求平均后得到14个均值,170条轮槽共计得到2 380个均值。15把精铣刀加工的轮槽号如表4所示。 表4 15把精铣刀加工轮槽表 汽轮机转子轮槽加工过程复杂、成本高、产品质量要求严格,因此需决策最优换刀时间。本文以基于相似性的铣刀剩余寿命预测算法[26]作为验证算法,该算法适用于对监控数据进行数据挖掘,并广泛应用于加工领域的刀具剩余寿命预测,通过对比分析优化前后数据的预测结果来检验AE数据特征值准确性的优化效果。 以计数、反算频率和信号强度数据为例,计算结果如图6所示,由圆心向外坐标为准确率,外圈数字为轮槽号。计数、反算频率和信号强度准确性集中在(0.945 00,0.950 00),最小值0.929 87为55号轮槽的计数属性。 14个AE数据特征值的权重,计算结果如表5所示。 将AE数据特征值加权平均得到以轮槽为单位的准确性评价结果,如图7所示,最低点0.895 95为58号轮槽,较次为43号轮槽,准确率为0.899 04,170条轮槽的准确率均值为0.916。 表5 AE数据特征值权重表 对评价结果进行分析以筛选待优化数据。如图6所示,图中出现多处凹陷,凹陷分为绝对凹陷与相对凹陷。绝对凹陷处点的准确率低,数据有待优化;相对凹陷处,其周围点的准确率总体水平较高,仅在该点处产生轻微下凹,其准确性无需优化。 根据上述原则,标记2 380个准确性结果中所有的绝对凹陷点(称为异常点)作为待优化数据。异常点标记方法为:从圆心开始向外逐点标记,直到某点的准确率不再位于后8.4%就停止。8.4%为动态标准,根据实际数据调整。该值过大造成数据过度优化,过小则造成数据欠优化。本文中所有轮槽的准确率均值为0.916,因此取8.4%作为标记标准。 刀具寿命预测以铣刀为单位,为便于选择数据集进行优化,以每条轮槽为单位统计包含5个及以上异常点的轮槽数(称为异常轮槽),并以铣刀为单位统计每铣刀包含的异常轮槽数,统计结果如表6所示,5号铣刀异常轮槽数高达9条,1、10号铣刀分别包含4条异常轮槽,14号铣刀包含3条异常轮槽,这4把铣刀的AE数据特征值准确性较差。 表6 15把精铣刀异常轮槽统计表 依据上述结果对AE数据特征值进行准确性优化,建立两个数据集D1,D2,每个数据集包含6把铣刀对应的监控数据,将准确性较差的1、5、10、14号铣刀分别分配给两个数据集,具体对应铣刀号D1={5,6,7,8,10,15},D2={1,3,4,12,13,14}。每个数据集中,将异常点作为待优化数据,其余为非优化数据,非优化数据用于建立哈希表,E2LSH_kNN优化参数如表7所示。 表7 E2LSH_kNN算法结构 将优化前后的AE数据应用于基于相似性的铣刀剩余寿命预测,用平均绝对误差(MAE)和均方根误差(RMSE)衡量预测结果,误差单位为轮槽,即预测的与实际的铣刀可加工剩余轮槽数之间的差异。结果如表8所示,优化后数据集1的MAE降低了0.309个轮槽,RMSE降低了0.355个轮槽,优化百分比分别为32.95%与32.55%;数据集2的MAE降低了0.677个轮槽,RMSE降低了0.702个轮槽,优化百分比分别为40.29%与36.51%。 表8 AE数据优化前后铣刀剩余寿命预测算法结果对比 传统监控数据处理方法主要包括指数平滑去噪、基于距离的离群点处理、最小协方差估计和孤立森林,因此选上述方法对数据进行优化处理并用于铣刀剩余寿命预测,结果如表9所示,其中方法1代表本文所提数据优化方法。图8表示各方法下MAE,RMSE的变化量,由表9及图8可见,对于数据集1,各数据优化方法均对预测误差减小起到正向作用,其中方法1的效果至少3倍优于其他方法;对于数据集2,只有方法1有效降低了预测误差,而其余4种方法均对预测准确性起到负作用,且误差增大量数值接近。 基于上述结果,方法1对不同数据集均有优化效果,对初始数据集选取不敏感;其次,方法1对数据优化的效果优于其他4种方法,因方法1可在高维数据中分别针对单条记录的每一维数据进行独立分析,因此能精准选择优化数据,避免过度优化以保存原始数据特征。而指数平滑去噪虽可进行单维度数据处理,但平滑程度较难把控,易损失数据原始特征;其余3种方法对数据处理的最小单位为整条记录,不能针对单维数据进行独立分析,不可避免地产生过度优化,甚至对预测效果产生负作用。综上所述,本文提出了基于测量不确定度的数据准确性量化评价方法,并从数据质量优化的角度有效提升了铣刀剩余寿命预测的准确率,验证了数据量化评价与优化的重要性与必要性。 表9 5种数据优化处理方法下铣刀剩余寿命预测误差对比表 本文通过采集转子轮槽AE数据,构建测量不确定度与数据准确性的联系,结合E2LSH_kNN对数据准确性进行量化评价及优化,使得铣刀剩余寿命预测算法准确性有效提升。同时,对比指数平滑去噪、基于距离的离群点处理、最小协方差估计与孤立森林优化处理效果,验证了测量不确定度法评价数据准确性的实用性和有效性,以及在数据分析前进行数值质量评价和优化的重要性和必要性。 本文测量不确定度法中以高斯函数进行准确性映射,在确定高斯函数参数时,需要实验人员根据经验综合考虑数据结构、数据获取方式、数据使用途径等条件。因此,如何综合考虑各个因素,使得参数选择更加合理、快速、体系化,以应用于不同生产加工现场将是下一步需要研究的问题。
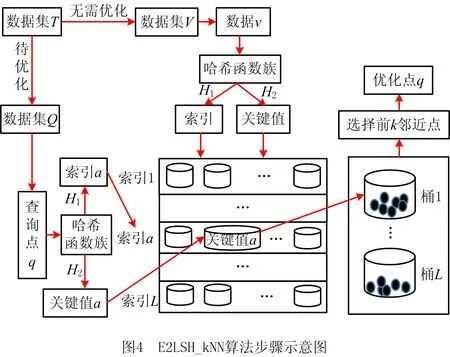
3 应用实例

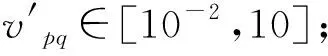



4 结束语
