例谈问题的引导，让学生想问、会问

李美亚

数学中的可能性问题就是概率问题，是指随机事件在相同情况下，可能出现也可能不出现的情况。小学六年级数学下册中《可能性》的复习教学，目标是通过复习，让学生进一步体会事件发生的可能性的含义，知道可能性是有大小的，会用分数表示一些简单事件发生的可能性大小，进一步体会可能性与现实生活的密切联系，培养简单的推理能力。在教学中采用问题引导，让学生发现真问题，会分析问题，并能解决问题。

天气逐渐热起来，下午的教室里更是又闷又热，我一走进教室，就听到孩子们在说“要是有空调就好了”，我顺着学生的话说“最近我在网上看到一款风扇广告，说这个风扇风力大、又省电，有空调的效果。大家认为能不能买？”，话题一出，同学们议论起来，认为可以买的原因是因为广告宣传的好，认为不可以买的原因是没有看到用户评价。经过辩论后，最终大家讨论的结果是：由于在日常生活中并没有用户使用体验数据和问卷调查等的统计，不能做到全面的分析和准确的判断，风扇使用效果的好坏存在不确定性，需要调查、分析后，再决定买不买。如果调查结果显示，被调查用户中大部分评价好，说明风扇优良的可能性大，就可以买。

通过创设轻松活泼的教学氛围和学生的活动，借助生活中的实例，让学生理解和掌握关于可能性的知识。

接着，我出示了这样一题：

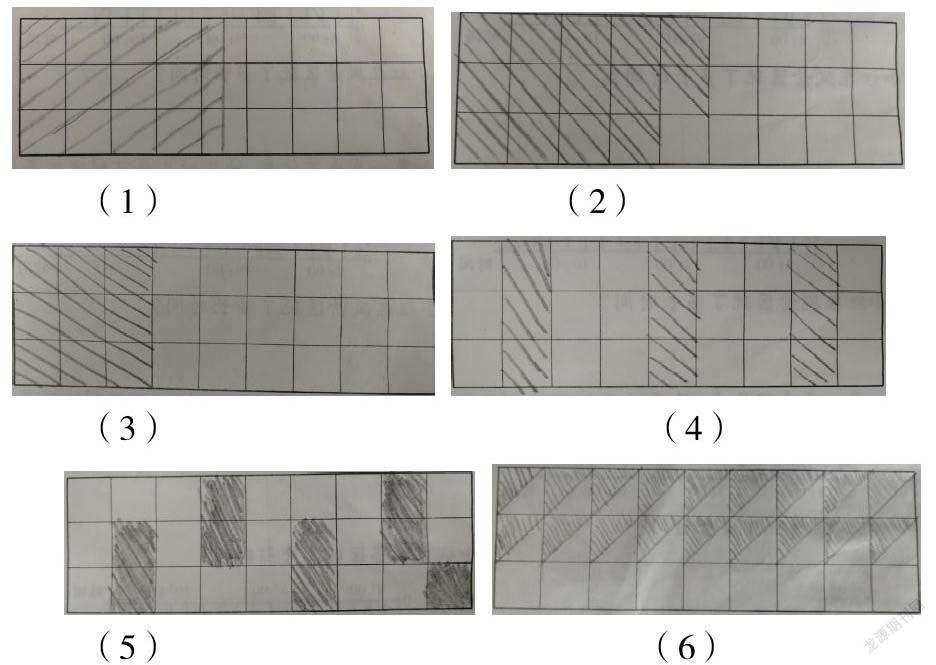
下图是一个长方形纸盒的底部，在下面的方格中涂上颜色。任意向纸盒中掷一枚骰子，是骰子落在涂色部分的可能性是落在空白部分的50%。

问题引导一：初步感知、明晓——“你有什么想说的？”

生1：我知道共有27格。

生2：我知道涂色部分应占总格数的50%。

生3：我知道涂色部分的面积应该是空白部分面积的50%。

……

问题引导二：激发求知欲——“你有什么想问的？”

（一）提出自己的疑惑

生1：如果涂色部分占总格数的50%，那27格的50%是13.5格，格数不是整数，怎么涂色？

生2：“涂色部分的面积是空白部分面积的50%”中空白部分是总格数27格吗？如果空白部分不是27格，那是多少格？

……

（二）学生思考，解题，同桌交流，展示学生涂色作品。

（三）再质疑——“此时你又有什么想问的？”

生1：图（1）和图（2）涂色部分表示27格的一半吗？

生2：题目要求“骰子落在涂色部分的可能性是落在空白部分的50%”，显然骰子落在空白部分的可能性要大，那图（1）、图（2）中骰子落在的空白部分的可能性大一些吗？

生3：图（3）、图（4）、图（5）涂色部分都是9格，涂法不同，这些涂法有什么特殊意义吗？

生4：图（6）涂色部分算几格？为什么要这样涂？它跟前面几种涂法有什么本质上的区别吗？

生5：上面6种涂法哪些是正确涂法？还有其他正确涂法吗

这些同学的疑惑一提出，教室里沸腾起来，小组里展开了激烈的讨论。

问题引导三：独立再思考、分析——“你有什么想解决的？”

（一）自由发表

生1：总格数27格的50%是指总数的一半，也就是13.5格，图（1）和图（2）涂色部分能表示“一半”，所以这是27格的50%可以这样涂。

生2：通过观察，图（1）和图（2）中涂色部分和空白部分一样大，也就表示骰子落在涂色部分和空白部分的可能性一样大，所以不符合题目要求，不能这样涂。

生3：根据“涂色部分的面积是空白部分面积的50%”，可以把涂色部分看做1份，那么空白部分就是2份，这样总数27格就被平均分成了3份，每份是27÷3=9格，也就是涂色部分是9格，空白部分是18格。所以图（3）、（4）、（5）涂法正确。

生4：图（6）涂色部分可以看作18个半格，也就是9格，所以涂法正确。

生5：我的涂法是图（5），这样涂是为了使涂色部分均勻分布，使骰子落入涂色部分的可能性更符合题目要求，所以图（5）和图（4）比图（3）更准确。

（二）引发争议，深度问题出现

1、 第5个同学的观点得到了很多同学的共鸣，好多同学认为图（4）、图（5）比图（3）涂法更准确，但也有少数同学认为图（3）和图（4）、（5）涂法意义一样，没有“更准确”之说。

2、有学生指出：如果按生5所说观点，那图（6）的涂色部分的分布岂不是更加均匀、更加准确？

3、学生再质疑：按图（6）涂法，如果骰子落在某一个一半涂色的方格内，那算是落入涂色部分，还是落在空白部分？难道是由骰子的大小决定落入部分的可能性？

4、学生假设：做10次这个实验，结果不明显，那如果做100次、1000次、10000次或者更多次，是不是就能解决“更均匀”、“更准确”的问题？

（三）小组讨论，解疑，概括总结，得到结论

经过几轮的：

出现结果→质疑→出现新问题→出现新结果→再质疑→再出现新问题→再出现结果→得到结论结论：数学中的可能性问题就是概率问题，需要大量实验来说明可能性结果，本题中只要涂色部分是9格就符合题目要求，不在乎涂色区域的选择。

本教学片段中，使用了三个问题引导：

首先提出“你有什么想说的？”，意在让学生初步感知，找到问题中已知信息。

再次提出“你有什么想问的？”，意在让学生经历分析问题和寻找自己“知道的”和“不知道的”的过程，主动提出自己“知道的内容”或“不知道的内容”，用提问的方式激发学生求知欲和探索欲。

最后提出“你有什么想解决的？”，经过前两个环节的问题引导，本环节的实施就水到渠成，学生带着浓厚的兴趣和自信“帮助大家”解决问题，但是在解决问题的过程中又引发了新的问题和更深层次的问题。学生思维就在“问题”、“解决问题”、“新问题”、“解决新问题”中不断跳跃，思维能力得到了进一步拓展。