设计地震下铁路简支梁桥支座水平地震力计算方法研究

王春阳, 刘正楠, 张永亮, 李晓钟

(兰州交通大学 土木工程学院, 甘肃 兰州 730070)

0 引言

在广泛分布的中小跨桥梁体系中,支座是连接桥梁上下部结构的重要构件。地震作用下支座的状态直接决定桥梁上下部结构的损伤情况,支座的破坏重则引起落梁,轻则导致支座螺栓剪断或拔出、移位,而完好的支座会将上部结构的惯性力引入桥墩,因此下部结构往往是桥梁结构的易损构件。2008年汶川地震中宝成铁路支座锚栓剪断、支承垫石破坏、摇轴支座横向错位等震害普遍发生[1],其中水关渭河简支梁桥震后固定支座中钢板与螺栓均被剪断,沿线116个支座破坏,码头大桥水平限位装置破坏;关庄渭河大桥梁体横向滑出,支座销轴限位挡板螺栓剪断[2-3]。可见,地震中支座是铁路桥梁的薄弱部位。

目前,关于支座的水平地震力计算方法各国规范均有涉及。我国现行《铁路工程抗震设计规范(GB 50111—2006)》[4](以下简称铁路抗规)指出简支梁采用静力法进行设计验算。现行的铁路简支梁桥支座通用图(1)《TJQZ—通桥8361》.北京:中铁工程设计咨询集团有限公司,2013.中支座水平地震力依据地震加速度峰值确定,取15%～40%的竖向承载力不等[5]。我国现行《公路桥梁抗震细则(JTG/T 2231-01—2020)》[6]中指出规则桥梁支座水平地震力计算应考虑相应方向上的加速度反应谱值,并区分了采用不同支座类型、不同结构体系的计算方法。台湾《铁路桥梁耐震设计规范》[7]指出支座应按照容许应力法设计。日本《铁道构造物等设计标准及解说—抗震设计》[8]中指出支座的设计水平地震力按下部结构的屈服震度与考虑列车荷载的上部结构的重量乘积确定,若下部结构屈服震度较大,还应进行L1地震动(对应我国设计地震)的加速度反应谱计算,在两者之间合理取值。美国《加州抗震设计规范》[9]中支座被视为牺牲构件,没有给出明确的设计计算方法。美国AASHTO桥梁设计规范[10]仅给出了桥梁设计采用不同类型支座时的几何尺寸、材料性能等要求。欧洲规范Eurocode 8[11]指出,固定支座的设计地震作用效应通过承载力实际确定,并且应设附加连接作为第二道防线。可以看出对于支座水平地震力的计算,各国规范还很不完整,相比而言日本规范给我们较大的启发。国内外学者对于固定支座设计计算方法的研究鲜有报道,但关于支座损伤状态及恢复力模型的研究成果[12-13],如支座损伤的咬合、干摩擦[14],以及固定支座破坏对桥梁地震反应的影响等方面的研究[15],为铁路简支梁桥支座水平地震力的合理计算提供了极有价值的参考。

基于此,本文以一跨径为32 m的铁路简支梁桥圆端形实体重力式桥墩为研究对象,提出利用反应谱计算支座水平地震力时桥墩合理截面的选取方法,并对规范静力法、反应谱法、简化反应谱法计算支座水平力的差异进行比较,提出支座水平地震力计算方法的合理建议。

1 现行铁路抗规支座水平地震力的具体计算方法

设计地震作用下,对于梁式桥支座水平地震力的计算,现行铁路抗规给出了两种计算方法:静力法和反应谱法。静力法无法考虑桥梁动力特性及所处的场地条件等;反应谱法虽然可以克服静力法计算存在的不足,但铁路抗规中仅指出采用反应谱法计算连续梁。

铁路抗规中指出,静力法计算简支梁顺桥向的支座水平地震力如式(1)所示,在考虑1.5的动力放大系数及0.05的活动支座摩擦系数的基础上进行代数运算:

FhE=1.5Ag·md-∑μRa

(1)

式中:FhE为固定端的水平地震力;Ag为地震动峰值加速度值;md为简支梁-孔梁和桥面的质量;μ为活动支座的摩擦系数,取0.05;Ra为活动支座反力;∑μRa为活动支座摩阻力之和。

静力法计算简支梁横桥向的支座水平地震力如式(2)所示,同样考虑了1.5倍的动力放大系数。

F′hE=1.5Ag·mb

(2)

式中:F′hE为桥墩墩顶处的水平地震力;mb为简支梁-孔梁和桥面的质量与墩顶活荷载反力换算质量之和。

一是在资金使用管理环节，制定了《赣州市财政扶贫专项资金管理办法》，对资金的使用范围、审核拨付和管理监督等进行了明确。同时，对所有纳入整合的财政涉农扶贫资金要求按照中央、省“专项扶贫资金管理办法”的规定管理和使用，做到资金管理监督全覆盖。

反应谱分析作为一种等效静力法,可以考虑各阶振型的贡献,其组合方式通常有SRSS (Square Root of Sum of Squares)、CQC (Complete Quadratic Combination)和ABS (Absolute Value)法。它能充分考虑结构动力特性与不同场地类型之间的耦合反应,但在设计反应谱法计算中对于桥墩截面有效刚度的取值没有明确的定义,因此现行铁路抗规中关于支座水平地震力的计算尚存在较多的不确定性。

2 工程概况及抗震计算模型

以某跨径为32 m的铁路简支箱梁桥为研究对象,主梁采用标准图(2)中铁工程设计咨询集团有限公司.《通桥(2008)2221A—Ⅱ》.北京:铁道部经济规划研究部,2008.,上部结构总质量为1 269.6 t,下部结构采用圆端形实体桥墩。顶帽横截面尺寸为3.4 m×8 m,托盘底部尺寸为6.2 m×2.3 m。墩高5～20 m不等,并根据墩身高度分别采用直坡等截面和1:45的变坡变截面,桥墩配筋率为0.3%～0.4%。桥址位于Ⅷ度区,特征周期分区2区,设计地震加速度峰值0.2g。

如图1所示,采用单墩模型进行抗震分析,在5～20 m墩高范围内，每2～3 m选取一个代表性的墩高作为研究对象。由于单墩模型除梁体质量单元施加位置不同外，其他部分均相似，因此仅给出顺桥向计算模型作为参考。由图1可知，桥墩及承台采用梁单元模拟,在每个承台底分别设置6个线性弹簧模拟地基刚度,弹簧参数采用m法求出。上部结构质量采用质量单元模拟,顺桥向计算模型将梁体质量施加在墩顶处;横向无车计算模型将梁体质量施加在主梁质心处,并通过刚臂单元与墩顶节点连接;横向有车计算模型将梁体质量施加在主梁质心处,将列车质量施加在轨顶以上2 m处。选取5 m、12 m与20 m三种代表性墩高的纵向和横向1阶自振周期表示墩高由5 m增大至20 m时结构自振周期的变化趋势和增大范围。经计算,5 m、12 m与20 m桥墩的纵向1阶振型自振周期分别为0.245 s、0.545 s和0.931 s,相应的横向1阶振型自振周期分别为0.353 s、0.634 s和0.984 s。

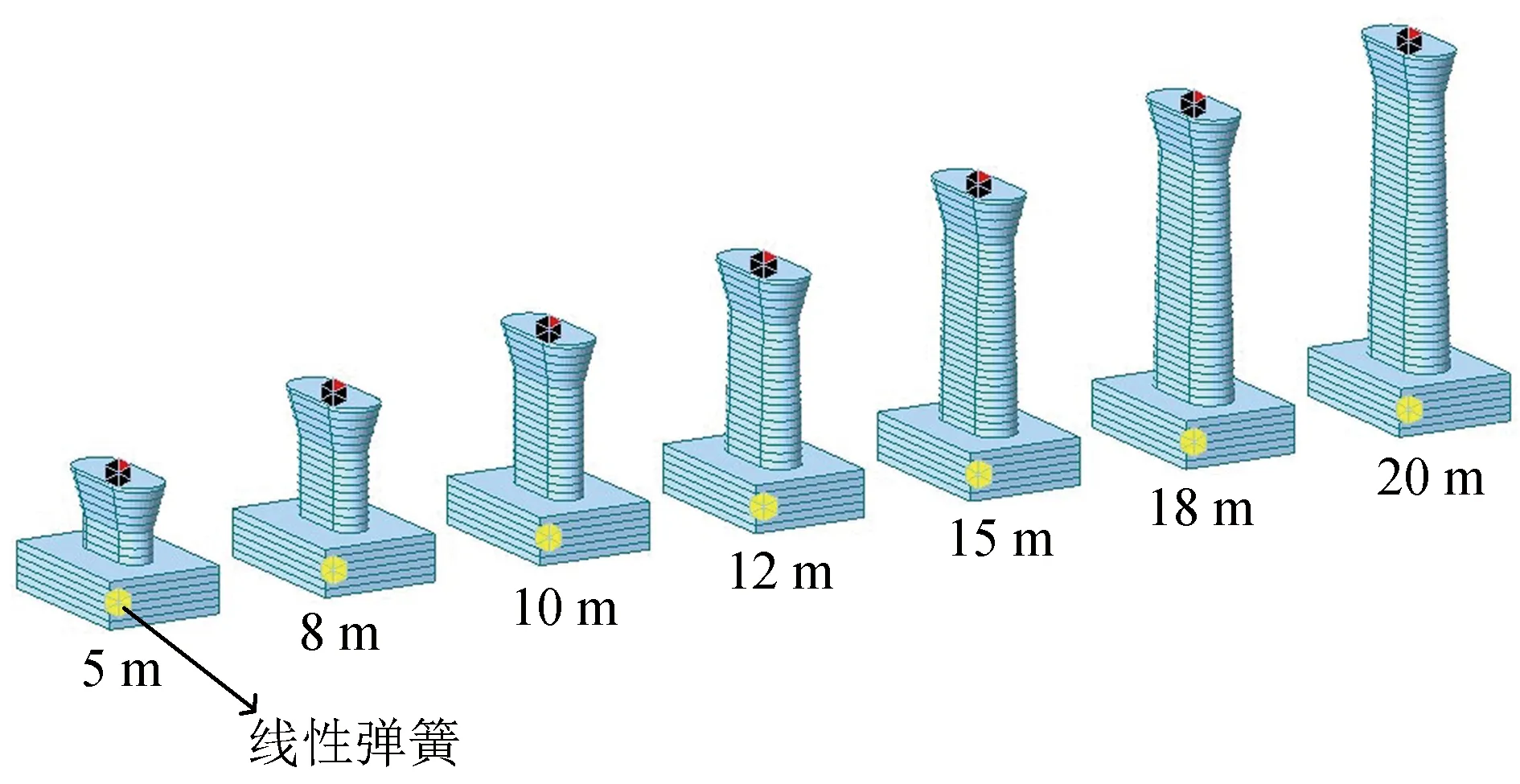
图1 顺桥向计算模型Fig.1 Longitudinal calculation model

3 反应谱分析桥墩截面刚度合理选取

首先对墩高5～20 m范围内的铁路简支梁桥墩进行墩底截面承载能力分析。由于设计地震对应中震,因此仅计算出截面开裂弯矩及开裂刚度,修正计算截面刚度。应用反应谱法计算设计地震下桥墩的地震反应,振型组合采用SRSS,输入的谱曲线采用铁路抗规规定的与场地特征周期相应的β曲线。地震动峰值区0.2g,对应规范中的Ⅷ度设计地震动。对3类场地对应下不同墩高的桥墩进行反应谱计算,同时为定量评价采用毛截面刚度和开裂截面刚度进行反应谱计算引起的墩底弯矩差异,定义误差因子λi:

λi=(Mm-Mc)/Mc-(Mk-Mc)/Mc

(3)

式中:i=1,2,3代表场地类型;Mm为采用毛截面刚度计算得到的墩底弯矩;Mc为桥墩的开裂弯矩,即受拉区最外侧混凝土达到极限拉应变时的弯矩,采用MIDAS Civil中的弯矩-曲率分析程序计算得出,再由弯矩-曲率曲线求得开裂曲率和开裂截面刚度;Mk为采用开裂截面刚度计算得到的墩底弯矩。

为合理判断选取反应谱分析所用的桥墩截面刚度,本文取配筋率0.3%和0.4%对桥墩进行计算,计算结果分别如图2、3所示。

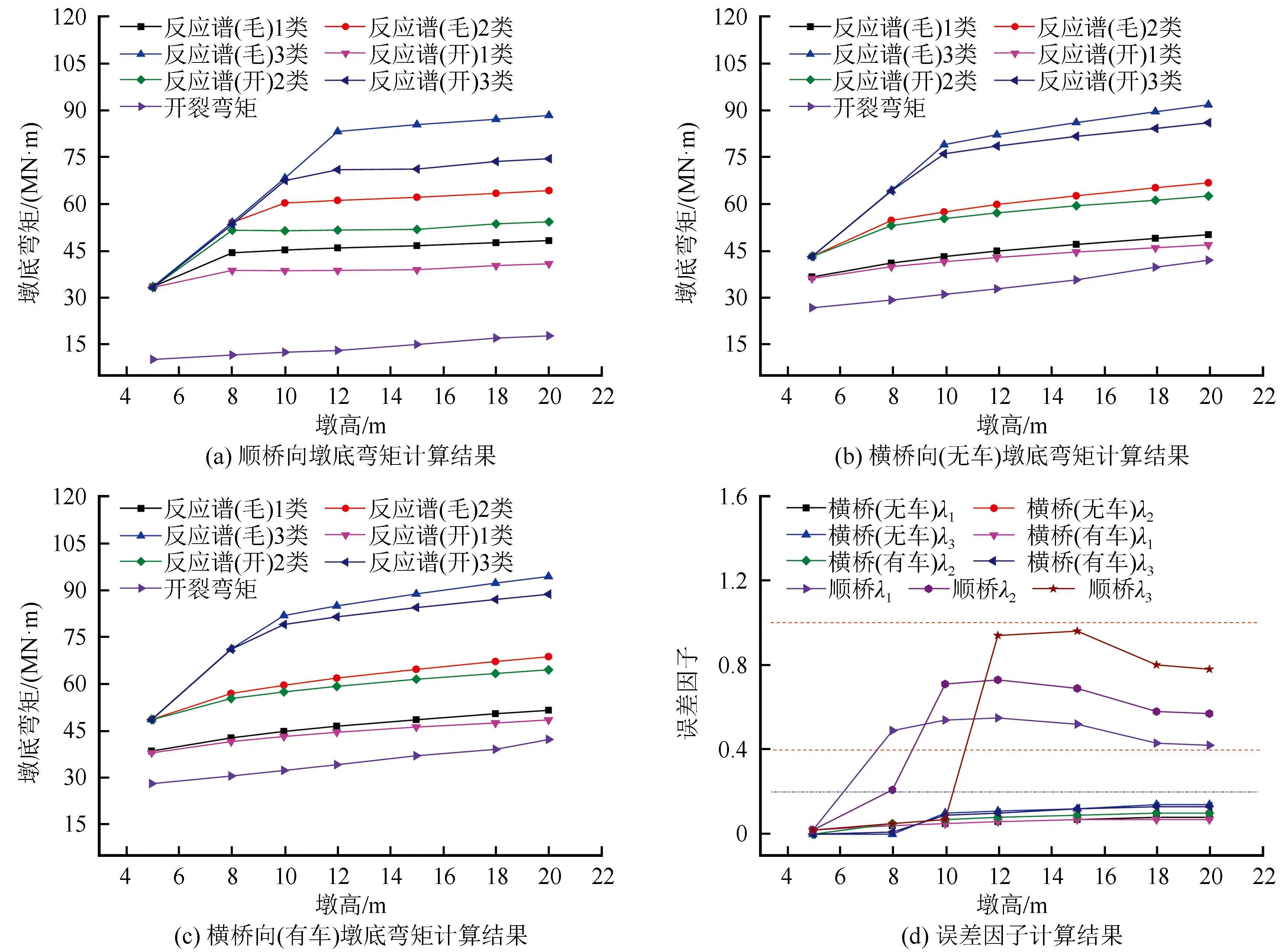
图2 0.3%配筋率桥墩地震反应Fig.2 Seismic response of pier with a reinforcement ratio of 0.3%

图3 0.4%配筋率桥墩地震反应Fig.3 Seismic response of pier with a reinforcement ratio of 0.4%

从图2、3的墩底弯矩计算结果可以看出,对于本文分析的墩高5～20 m的铁路简支梁桥墩,以毛截面为反应谱计算截面时,顺桥、横桥(无、有车)三种情况下,桥墩墩底弯矩均大于对应的截面开裂弯矩;以开裂截面为反应谱计算截面时,顺桥、横桥(无、有车)三种情况下,桥墩的墩底弯矩均大于开裂弯矩。由此可见,采用开裂截面刚度进行反应谱抗震分析更为合理。

统计发现,我国铁路简支梁桥墩的配筋率大多低于0.4%,因此建议位于高烈度区的铁路简支梁桥在设计地震作用下进行纵桥向反应谱分析时采用开裂截面。

4 铁路简支梁桥支座水平地震力合理计算方法

依据上述关于铁路简支梁桥反应谱分析时合理截面的选取和探讨,以开裂截面作为反应谱的分析截面,基于规范静力计算方法、简化反应谱分析法及反应谱法计算支座的水平地震力。其中简化的反应谱分析方法是通过有限元分析确定结构的第1阶自振周期,进而通过反应谱曲线确定动力放大系数,采用式(4)确定支座的水平地震力:

FS=αAgmb(d)

(4)

式中:FS为简化反应谱计算的支座水平地震力;α为第1阶周期对应的动力放大系数。

同时,为研究简化反应谱法与反应谱分析的差异及二者的使用范围,引入两个变量进行分析:定义变量ζ为放大系数,如式(5)所示;定义变量η为相对误差,如式(6)所示:

ζS(R)=FS(FR)/Fj

(5)

η=(ζS-ζR)/ζR×100%

(6)

式中:FR为反应谱计算的支座水平地震力;Fj=F′hE(FhE)为规范静力法计算的支座水平地震力;ζS为简化反应谱计算得到的放大系数;ζR为反应谱计算得到的放大系数。为便于观察在不同墩高条件下按规范静力法设计支座的安全性,在计算结果中设置危险区与安全区:当ζ>1时,代表反应谱计算值>静力法计算值,规范方法设计支座使之处于危险区;当ζ<1时,代表反应谱计算值<静力法计算值,规范方法设计支座使之处于安全区。

以0.4%配筋率的桥墩为例,进行反应谱法的对比计算,计算结果见图4、5。

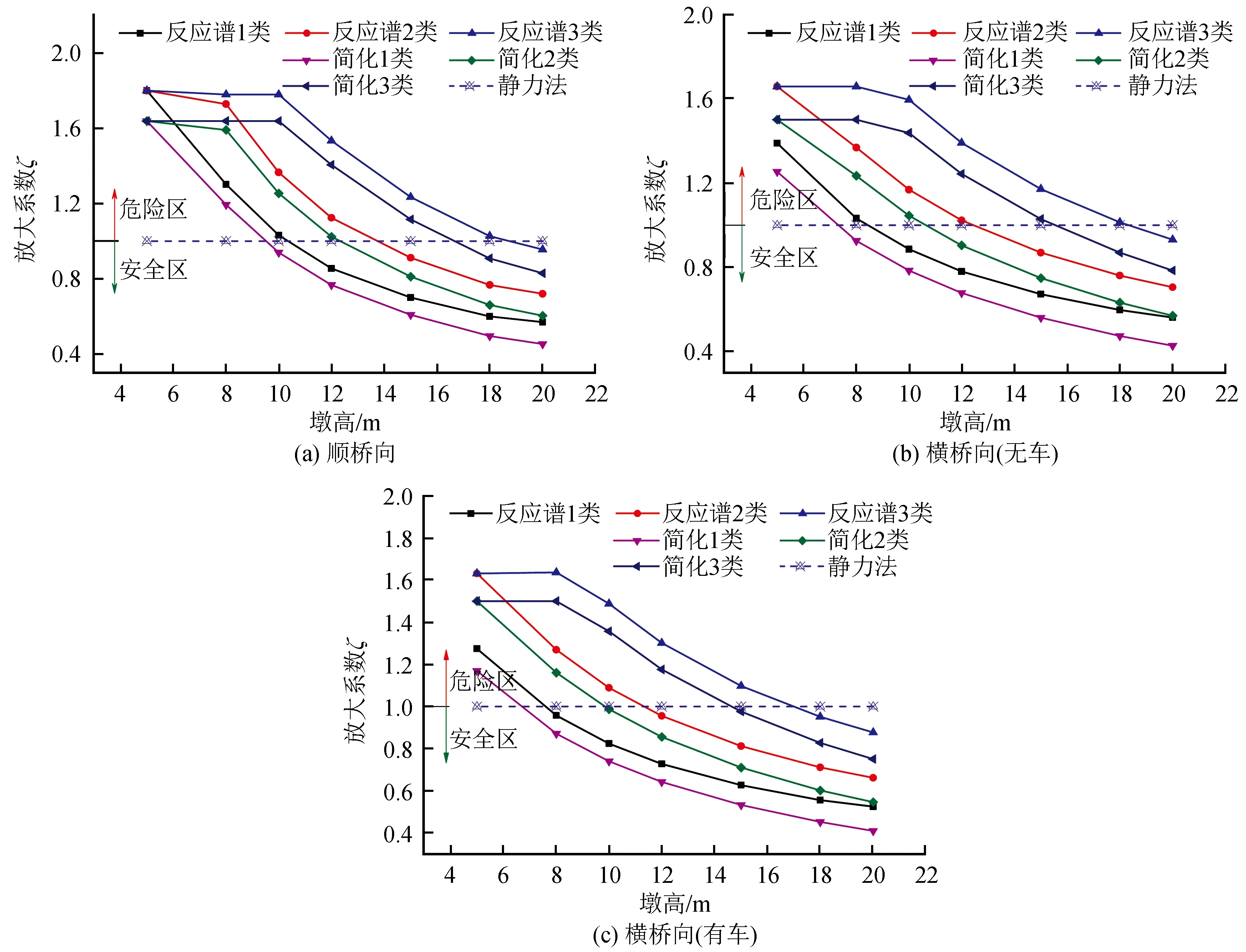
图4 支座水平地震力计算结果Fig.4 Calculation results of horizontal seismic force of bearing

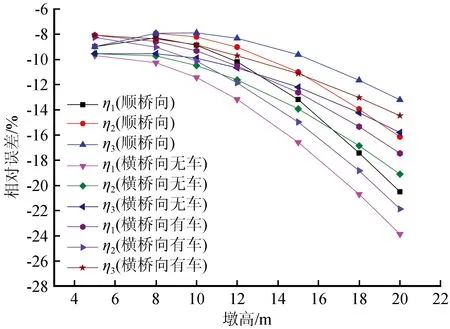
图5 相对误差Fig.5 Relative error

从图4中可以看出,对于不同的墩高和场地条件,按规范静力法设计支座可能造成设计值偏大或偏小,影响支座选型,导致实际地震中支座剪断破坏的概率增大。反应谱计算结果显示,随着墩高增加和场地条件好转,放大系数ζ呈减小的趋势。显然静力法无法考虑场地因素及桥墩的动力特性,很难准确计算出支座的水平地震力。

关于墩高变化及场地变化引起的支座水平地震力响应规律,以及简化计算方法与反应谱法的差异,可结合图5进一步说明,具体归纳为以下几点:

(1) 墩高变化对支座水平地震力计算的影响较为显著。顺桥向计算结果显示,在5～12 m的墩高范围内,按静力法计算的支座水平地震力小于反应谱法计算的结果,放大系数ζ>1,且在1.0～1.7之间变化,计算结果处于危险区,此时按规范静力法设计支座是较危险的;当墩高达到20 m时,按反应谱计算的支座水平地震力小于静力法计算的结果,放大系数ζ<1,计算结果处于安全区,此时按静力法设计支座是较为安全的。另外,桥墩越矮,放大系数ζ越大,这是由于矮墩的第1阶周期较小并与地震反应谱曲线的平台段对应,结构的动力效应对地震反应的影响较大,因此在设计地震作用下按静力法设计支座并不安全。

(2) 场地变化对支座水平地震力计算的影响也较为显著。顺桥向计算结果显示,3种类型场地条件对支座水平地震力的影响表现为:随着墩高的增加,放大系数ζ逐渐减小,由危险区过渡至安全区;2类和3类场地条件下,放大系数ζ多数大于1,在危险区占比较高,这是由于场地条件越差,反应谱平台段越长,动力效应就越明显。

(3) 计算支座的水平地震力时,采用简化反应谱法基本能代表反应谱法,可以较好地反映出计算结果的变化趋势。桥墩较矮、场地条件较差时,二者相对误差较小,5 m桥墩对应相对误差在10%以内,20 m桥墩对应误差最大达24%。总体上,随着墩高的增加,二者相对误差逐渐增大。

(4) 横桥向(有、无车)时,墩高变化、场地变化及两种计算方法的差异基本与纵桥向规律相似,此处不再赘述。

5 结论

本文以一墩高5～20 m、标准跨径32 m的简支梁桥为研究对象,考虑常规0.3%～0.4%的桥墩配筋率,结合场地条件,探讨了反应谱分析中桥墩截面的合理选择方法。基于规范静力法、反应谱法及简化反应谱法分析了纵桥、横桥(有、无车)的支座水平地震力,得到如下结论和建议:

(1) 桥墩越矮,设计地震作用下采用规范静力法计算的支座水平力与实际情况差异越大,将严重低估支座实际受到的水平地震作用。且相对于桥墩,支座明显为易损部件,这一点与实际震害现象基本一致。

(2) 设计地震作用下的支座水平力计算应采用反应谱法,且反应谱分析应结合桥墩截面状态选择相应的分析截面。对于我国铁路简支梁桥桥墩(尤其是顺桥向),应采用开裂截面刚度修正截面特性,进行反应谱分析。

(3) 桥墩越矮,场地条件越差,支座的水平动力效应也越明显,建议支座水平地震力采用动力法进行分析,以充分考虑结构的动力效应及场地的影响。

(4) 简化反应谱法基本能代表反应谱法,可以较好地反映支座水平地震力随墩高及场地条件变化的规律。