基于模型的数字式电液作动器智能控制方法*
2022-04-02赵天宇李文顶傅俊勇
赵天宇,吴 帅,李文顶,房 成,傅俊勇
(1.北京航空航天大学 自动化科学与电气工程学院·北京·100006;2.上海航天控制技术研究所·上海·201109;3.上海伺服系统工程技术研究中心·上海·201109)
0 引 言
电液式作动器由于体积小、响应快的特点,被广泛应用于智能机械、航空航天等工业领域。传统的电液式作动器采用比例式伺服阀作为阀控元件,通过控制作动缸筒两侧的压力流量,进而控制作动器系统的位置和速度。近年来,由于数字阀具备价格低、泄漏量小、鲁棒性高、稳定性好等优点,针对数字式液压系统的研究增多,数字式液压系统发展迅速,已经成为了液压系统的一个重要研究方向。故产生了数字式电液作动器,典型的数字式电液作动系统和控制特性是将多个高速开关阀构成阵列形式,形成数字阀,作为电液作动器的阀控元件来控制作动器系统的压力、速度和位置。目前,针对数字式电液作动器的研究范围较广,包含能效、集成结构等多方面,但主要研究集中在阀的构型尺寸设计和新型材料的应用上,针对被控对象的负载特性,以及如何选择和负载相匹配的数字液压系统构型等方面的研究还较少。现有的针对数字阀控制的研究可以分为单开关阀控制和开关阀阵列控制两部分。
数字液压系统中的单开关阀控制可以类比于电气系统中的脉冲宽度调制(Pulse Width Modulation,PWM)控制,单开关阀通过调节开关的时间实现离散的流体输入。理论上可以认为开关阀全开全关无节流损失,从而提升了系统的效率。离散流体在惯性和压缩性的滤波作用下,形成波动较小的压力连续变化,再通过液压执行器产生驱动力,进而控制负载力和负载运动。在负载的惯性和阻尼作用下,速度和位置的波动逐渐变小,近似于连续控制。国内外学者对控制算法进行了改良和优化,通过新型的PWM能够减少阀开关延迟时间,提高系统性能,增加系统带宽。
数字阀阵列则可以通过编码控制实现流量的近似控制,主要的编码形式包括不同流量增益的二进制编码(Pulse Coding Modulation,PCM)和相同增益的脉冲数量调制(Pulse Number Modulation,PNM)编码。PCM控制需要的阀数量较少,但每个阀的流量特性不一样,通常流量大的阀动态响应要低于流量小的阀,限制了系统动态特性的提高。PNM编码方式需要的阀数量最多,但优点在于只需要采用相同的阀,每个阀的特性一致,都可以采用小流量,有利于保证系统的动态响应。
在PNM编码的情况下,M.Linjama等采用脉冲频率调制(Pulse Frequency Modulation,PFM)解决系统在低速下跟踪性能较差的问题,实现了小于最小PNM的需求,提升了调节的精度。M.Paloniitty等提出了一种多阀脉冲宽度调制(Multi-Valve Pulse Width Modulation,MVPWM)算法,将控制量作为整个系统的目标,对各个开关阀联合脉冲调制。通过条件判断系统是PWM或是PFM,提升了位置跟踪精度。M.Ketonen等通过将独立计量阀系统与数字液压系统相组合,提出了一种数字式独立计量阀系统,对每一条节流边都进行独立控制。最终的实验结果表明,不同部分的能耗下降了约24%~42%。俞军涛等通过采用PWM和脉冲幅度调制(Pulse Amplitude Modulation,PAM)综合的方式对系统的信号进行控制,液压缸位置控制精度达到了1%。
采用多开关单元的组合数字阀可以通过数字编码控制实现近似的连续控制,具有可直接数字控制、抗干扰能力强、效率高等优点。但现在主要的难点在于组合构型的确定,如何选取和负载匹配的开关阀的数量和流量以及开关阀的频率,从而实现高精度的压力伺服和优越的动态性能。同时,多开关单元的复合控制是数字液压关键的一环,如何根据目前工况和目标状态快速准确地计算最优的编码,实现压力的高精度近似连续控制是一大难点。本文提出了一种基于模型的开关阀阵列智能控制算法,旨在实现开关阀构型和负载的精确匹配,以提升数字式电液作动器系统的控制精度。
1 数字式电液作动器结构建模
1.1 开关阀建模
本文采用的双集成高速开关阀的结构原理图如图1所示。
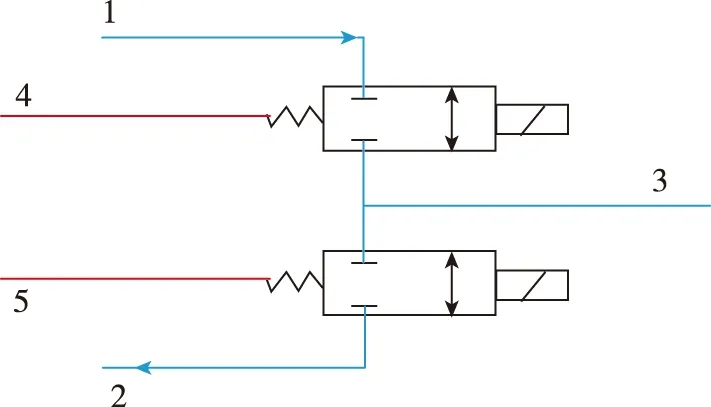
图1 双集成高速开关阀原理图Fig.1 Schematic diagram of double integrated high-speed on-off valve
双集成高速开关阀集成了2个电磁式开关阀,对外留出了3个液压接口,分别对应进油接口1、回油接口2和控制接口3;留出了2个电子接口,分别对应2个开关阀的电气控制接口4和5。通过给开关阀不同的信号,可以对开关阀的开关进行控制。当进油侧的开关阀开启,回油侧的开关阀关闭时,液压油从油源流过开关阀进入控制口,从而使外接系统升压;当进油侧的开关阀关闭,回油侧的开关阀开启时,液压油从控制口流过开关阀到回油口,从而使外接系统降压;当两侧开关阀都关闭时,外接系统压力保持不变。通过不同指令的控制,可以使开关阀组实现三种状态以及两位三通阀的功能。
电磁式开关阀通过电流驱动线圈产生电磁力驱动,在连接外部控制信号时,其等效驱动电路如图2所示。

图2 电磁式开关阀等效驱动电路Fig.2 Electromagnetic on-off valve equivalent drive circuit
开关阀的线圈在电路中可以等效为电感和电阻两部分,根据图2可以得到
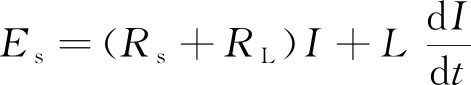
(1)
式中,为控制电源的电压;为电源的内阻;为高速开关阀的结构线圈电阻;为等效电路电流;为线圈的电感。
根据线圈特性可得
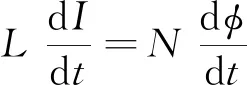
(2)
式中,为线圈匝数;为线圈总磁通量。
将式(2)代入式(1)可得
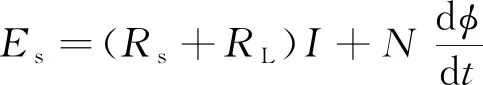
(3)
根据式(3)可以求出线圈的总磁通量,进而求出线圈产生的电磁力
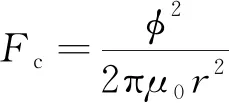
(4)
式中,为空气磁导率;为气隙处的磁极半径。
建立开关阀阀芯的运动方程
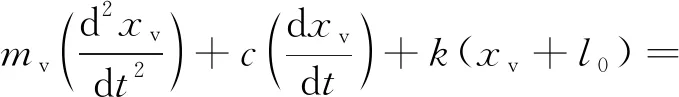
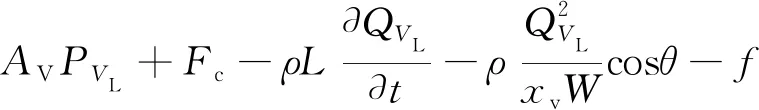
(5)
式中,为主阀芯的质量;为阀芯运动的阻尼;为弹簧的劲度系数;为弹簧的预压(拉)缩量;为球阀到液压缸流道横截面积;为开关阀负载压力;为流体密度;为球阀到液压缸流道长度;为开关阀流量;为阀口面积梯度;为回流方向与球阀轴向夹角;为滑动摩擦力。
建立开关阀阀芯的流量控制方程
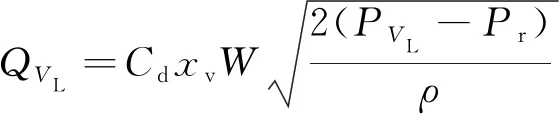
(6)
式中,为流量系数;为开关阀回油压力。
1.2 液压缸系统建模
本文采用的液压缸模型如图3所示。
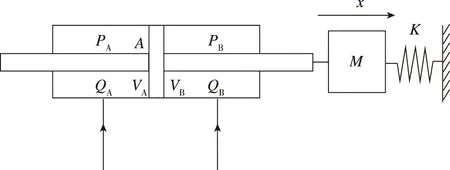
图3 液压缸模型Fig.3 Hydraulic cylinder model
忽略油液温度、油液黏度和管路压力的损失以及液压缸内部、外部泄漏。假设液压缸两侧有效工作面积相等,流体状态为层流,可以得到液压缸两腔的流量方程以及运动方程。
液压缸左腔流量方程为
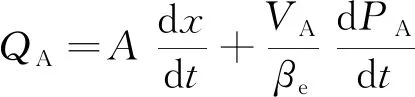
(7)
液压缸右腔流量方程为

(8)
运动方程为
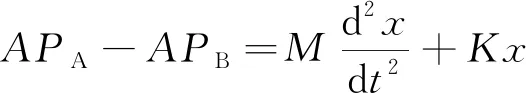
(9)
式中,为液压缸活塞位置;、为液压缸左右两腔流量;为液压缸有效工作面积;、为液压缸左右两腔压力;、为液压缸左右两腔有效容积,假设两侧初始容积相同,即A=B=;为流体体积弹性模量;为负载质量;为负载弹簧刚度。
设负载压力=-,则有液压缸系统负载流量

(10)
根据计算得出的负载流量可以用于后续对所需开关阀数量的计算。
2 位置控制算法
数字式电液作动器的控制流程设计如图4所示。

图4 智能控制算法流程图Fig.4 Flow chart of intelligent control algorithm
模型观测器通过位置、速度和压力输入判断模型的状态,并将压力状态输出到智能控制器中。智能控制器根据输入的压力状态和位置状态对开关阀开启数量以及开启时间进行实时智能调控,完成控制量的构建。通过控制液压缸活塞两端的流量大小调控液压缸位置,实现系统位置指令的实施调控。整个位置控制智能算法由模型观测算法和智能控制算法两部分组成。
2.1 模型观测算法
数字阀控作动器的原理图如图5所示。
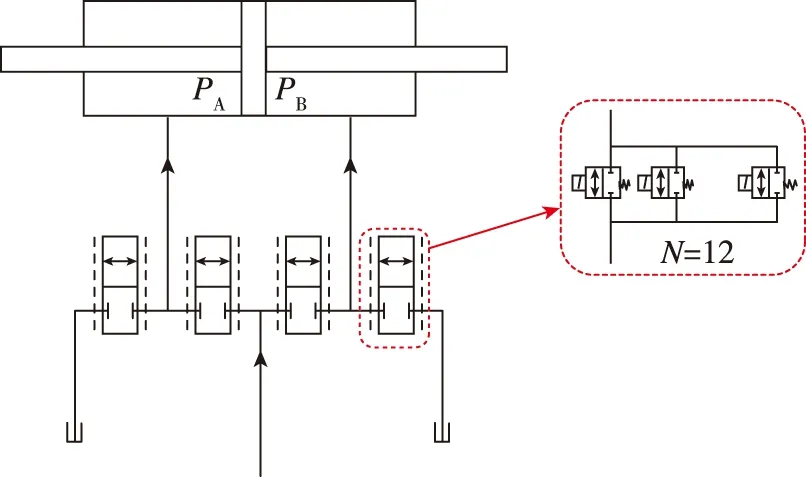
图5 数字阀控作动器原理图Fig.5 Digital valve-controlled actuator schematic diagram
设定作动器活塞的最大速度为0.1m/s,则驱动作动器以相应速度运动所需流量为
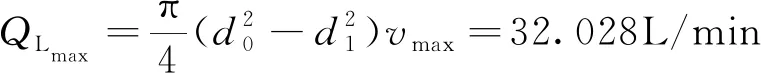
(11)
式中,为活塞直径,根据实际火箭喷管作动器的参数,取105mm;为活塞杆直径,取65mm。
本文使用的双集成高速开关阀,考虑理想情况,仿真中开关阀全开流量为定值。由于本文只对数字式电液作动器进行仿真分析,故考虑系统的管路为理想状态,即不考虑传递时的能量耗散以及内泄漏等因素,可求得在理想状态下进行仿真时,驱动活塞达到最大速度所需的开关阀最小数量为

(12)
式中,为驱动活塞达到最大速度所需的开关阀最小数量;为双集成高速开关阀的全开流量,为3L/min。
即最少需要单侧11个开关阀提供升压或降压时所需的流量。本文液压缸每侧采用12个开关阀控制升压,12个开关阀对液压缸采用独立负载控制。整个数字式电液作动器系统由64个开关阀构成。数字式电液作动器与传统电液作动器最大的不同在于其控制量是离散的,通过传感器给出系统的活塞位置和两端压力,给入到智能控制算法之中。而如何建立正确的位置指令和开关阀开启数量间的关系至关重要,所以需要一种基于模型特性的模型观测器对模型的状态进行预测,建立位置指令和开关阀控制指令的方式。
本文提出了一种新型的模型状态观测器,采用动态查表的方法。动态查表法的原理图如图6所示。
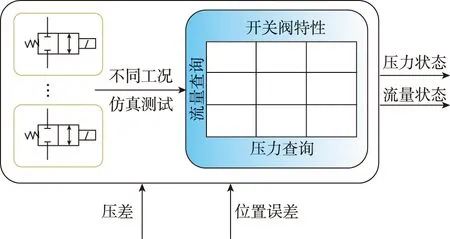
图6 模型观测器动态查表法原理图Fig.6 Schematic diagram of dynamic table method
通过对多个相同种类的高速开关阀在不同的工况下进行测试,得到单个开关阀在不同压差下得到不同体积流量所需的开启时间数据,并将其构成一个二维的表格,即得到了模型状态观测器中的开关阀特性表格。表格具备压差和体积流量两个维度。对液压缸两腔的压力进行实时监控,可以计算得到开关阀两端压差;对活塞的位置进行实时监控,可以计算得到与位置指令间的位置误差,进而求出推动活塞到目标位置所需的体积流量,从而完成位置指令到压力状态之间的构建。
对于查表法的精度,有两个较为重要的影响因素:
1)表格的坐标精度。通过对表格的压力坐标和体积流量坐标进行精细划分,能够尽可能地逼近连续的开关阀特性,进而增加查表法的精度。但是无限制地对表格进行扩展会增加占用空间,对硬件系统造成负担;同时,过度拓展表格还会增加查表所需要的时间,使状态预测的速度减慢,可能会影响系统的实时性。在实际设计过程中,针对这两点限制需做出一定的妥协。
2)开关阀测试数据的准确性。在进行实际实验时,所需的开关阀特性不尽相同。对于同型号批次的开关阀来说,也会由于结构上的误差,而导致最终的特性有所不同,需要针对不同型号不同特性的开关阀进行不同的设计,构建不同的表格;对于仿真实验来说,由于仿真模型的特性完全相同,故可以保证开关阀仿真测试数据的准确性和稳定性。
通过查表的方法可以避免在对作动器的位置进行控制时对开关阀的特性进行实时的计算,因此降低了整个系统的复杂性,逻辑较为简单。同时,由于开关阀开启时间通过查表而不是通过模型实时计算得出,故大大降低了控制时所需的时间,增加了整个系统的实时性,实现了对系统的高精度控制。
2.2 智能控制算法
数字式电液作动器系统的智能控制算法采用PWM和PNM两种调节方法相结合。
PWM调节用于单开关阀的控制。PWM通过对一系列脉冲的宽度进行调制获得所需要的等效波形,根据在2.1节中求出的单开关阀开启时间,通过调节一个周期内的占空比调节信号和能量,使得在一个周期内开关阀的控制信号等于单开关阀开启时间的占比。通过PWM对单个开关阀的调节能够控制单个开关阀的流量,使得整个系统的调节机制更加灵活。通过PWM调节可将压力状态和所需要的单个开关阀的开启时间相对应,从而对开关阀的开启时间进行构建。
多开关阀并联系统的一个基本特征是输出量量子化,这就需要通过一定的编码方式使得连续的信号变为离散的信号。常用的调节方式有两种,PNM调节和PCM调节。PCM调节的每个状态组合给出不同的输出值,每一个状态的输出值是上一个状态输出值的2倍,即其分辨率可以成倍地提高,这在理论上可以大幅地减少阀门的数量,因为只需要很少数量的开关阀就可以进行精确的控制。但是PCM调节方法需要不同尺寸的阀,每个阀的流量增益不一样,尺寸也不一样,不利于批量加工,而且动态响应特性会增加控制的难度和最终控制特性的不确定性。故而本文采用PNM调节对开关阀组合进行控制。本文液压缸单侧由12个开关阀组组成,每个开关阀组存在开关,即“0”和“1”两种状态,故整个系统的状态组合总数为2,如图7所示。
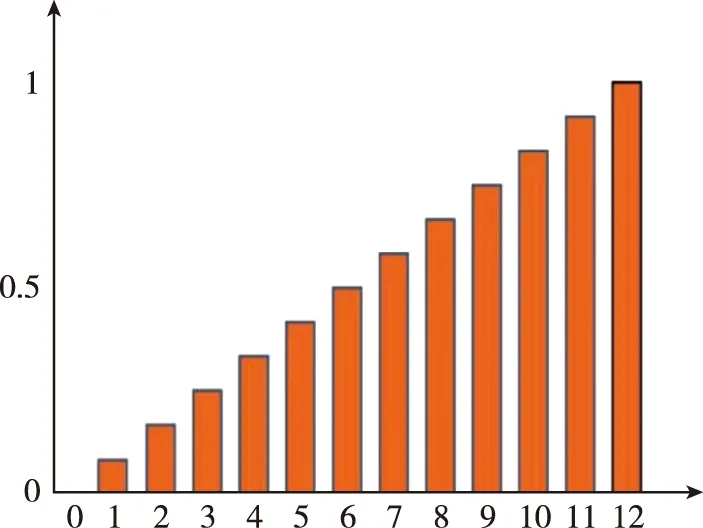
图7 PNM调节时数字阀组的输出量Fig.7 Output of the digital vales when controlled by PNM
采用PNM调节时,每个组件的大小相同,此时输出值的个数最小,输出值的最大值为+1,将单侧液压缸的流量分为12个区间,实现输出量的量子化。多开关阀并联系统的另一个基本特征是可以短时间保持状态不变,进而保持离散输出值。一旦选择了状态组合,且开关阀阀芯达到了指定的位置,输出就保持不变。通过PCM调节可将压力状态和所需的开启数量相对应,从而对开关阀的开启数量进行构建。
通过PCM和PNM协同对开关阀进行控制,能够最大程度上保证数字阀系统的精度。两种方法相结合能够弥补各自方法中存在的不足:由于在PCM中加入PWM,即通过控制多个开关阀的开启时间对作动器进行控制,可以在一定程度上减少系统所需开关阀的数量;同时由于在PWM中加入了PCM,单个开关阀不需要一直持续的工作,故一定程度上增加了系统的寿命和可靠度。
通过在仿真软件中进行联合仿真,可以验证智能控制器对数字式电液作动器的位置控制效果。
3 仿真试验及结果分析
3.1 仿真模型
根据仿真框图图8,在仿真软件中对基于模型的数字式电液作动器的模型进行仿真,可以在不同的仿真软件中分别建立基于模型的数字式电液作动器位置控制系统物理模型。
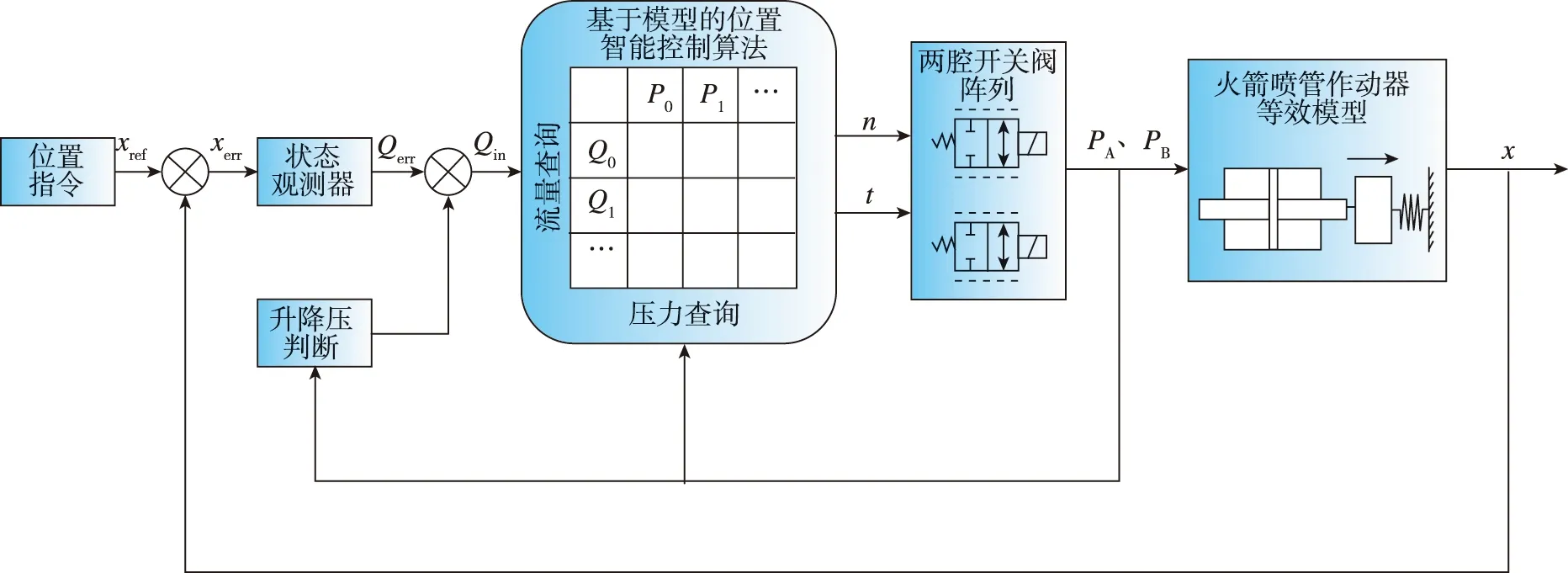
图8 数字式电液作动器智能位置控制系统仿真模型框图Fig.8 Simulation model of digital electro-hydraulic actuator intelligent controller
根据实际系统设置模型的各项参数,仿真所用的参数如表1所示。
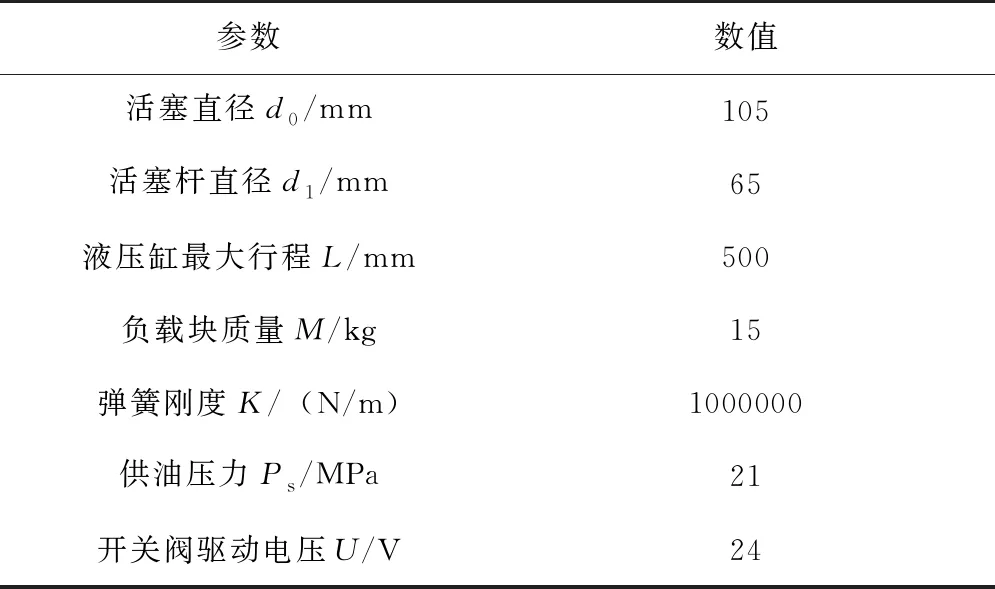
表1 数字式电液作动器仿真参数Tab.1 Simulation parameters of digital electro-hydraulic actuator
3.2 仿真结果及分析
由于设置作动器活塞的最大速度为0.1m/s,故设置幅值为100mm,频率为0.2Hz的正弦信号作为位置指令信号测量系统的输出,位置跟踪如图9所示,位置误差如图10所示,两腔压力变化如图11所示,左腔开关阀控制信号如图12所示。

图9 正弦信号跟踪曲线Fig.9 Tracking curve of sinusoidal signal
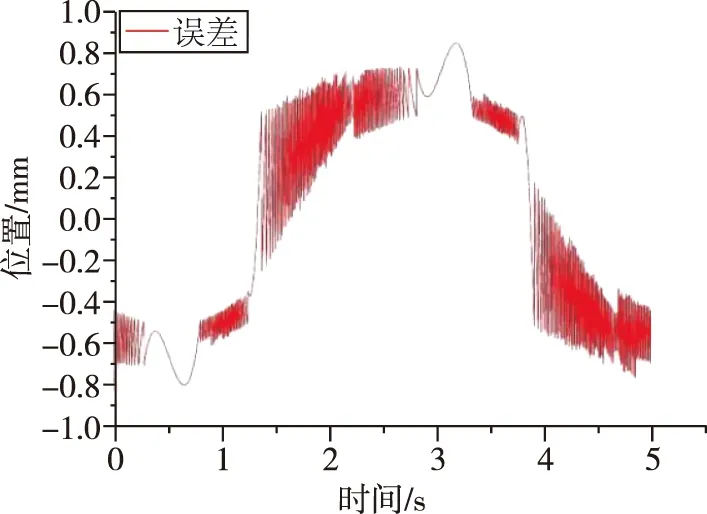
图10 正弦信号下的误差曲线Fig.10 Error curve of sinusoidal signal
如图9和图10所示,作动器活塞对低频正弦位置指令的跟踪精度达到了0.8mm,由于正弦信号的幅值为100mm,即最终的跟踪精度达到了0.8%,控制精度较高,控制效果较好。由此证明利用新型智能算法的数字阀系统能够实现对作动器的位置进行较为精准的控制,并且控制精度要优于传统的数字阀控制算法。由于在仿真中使用21MPa的油源对系统进行供油,压差较大,导致系统整体曲线容易出现振荡,对结果产生一定的影响,故整个系统所得到的仿真结果会稍大一些,后续仿真实验针对此种特点继续对控制算法进行改进。
如图11所示,由于数字阀系统通过控制液压缸两腔压力对位置进行控制,所以作动器两腔的压力曲线近似于正弦曲线;如图12所示,由于同时采用PWM和PNM进行控制,故开关阀的控制量与开启时间(在曲线之中表现为占空比)和开启数量相关,可以看到随着位置误差的变化,数字阀系统中的开关阀的开启数量和开启时间也实时变化,体现出数字式阀控系统的控制特性。
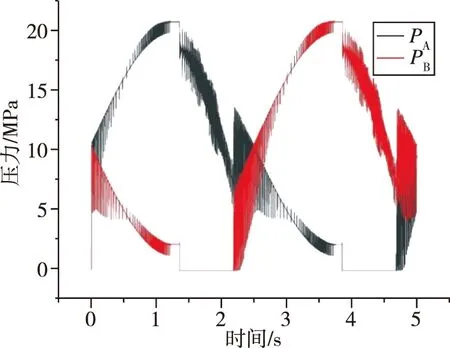
图11 两腔压力曲线Fig.11 Pressure curve of cylinder A and cylinder B

图12 开关阀控制量Fig.12 Control quantity of on/off valve
设置跟踪精度幅值为2mm的阶跃信号,跟踪结果如图13所示。
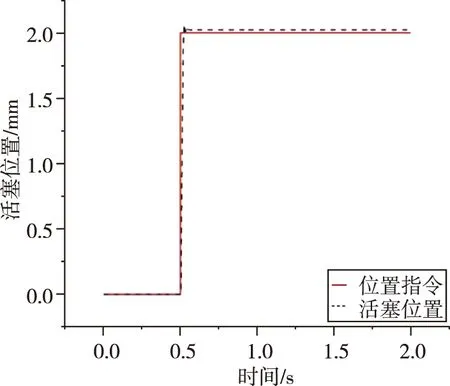
图13 阶跃信号跟踪曲线Fig.13 Tracking curve of step signal
从图13中可以看到,活塞对于幅值为2mm的阶跃信号能够进行快速的跟踪,调整时间约为0.001s,快速性较好。但是与活塞指令存在一定的稳态误差,这与控制算法中设置的误差带相关,通过进一步优化控制算法能够对开关阀进行更为精准的调控,减小系统的稳态误差。
设置幅值为2mm,频率分别为1Hz、2Hz、5Hz、10Hz、15Hz、20Hz的正弦信号作为位置输入信号,通过采集不同频率下活塞位置和位置指令之间的幅值比和相位差,对数字式电液作动器系统的动态特性进行测量,将结果汇总为系统的幅频、相频特性如图14所示。
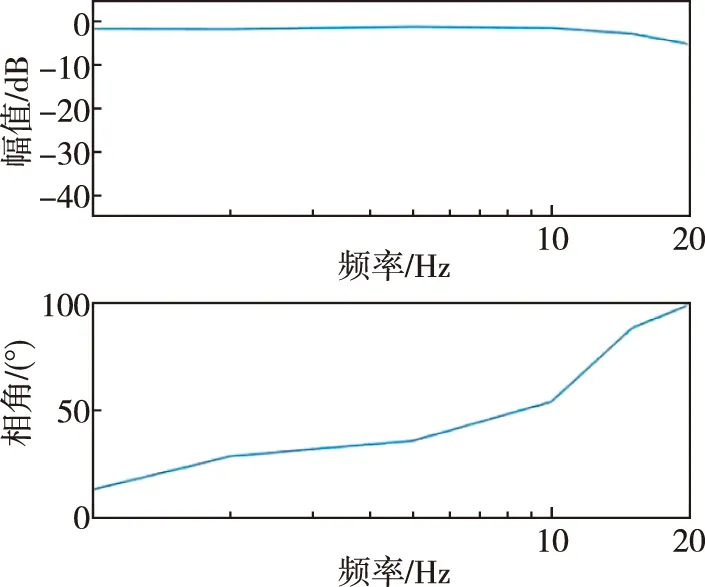
图14 幅频相频曲线Fig.14 Amplitude-frequency curve and phase-frequency curve
如图14所示,活塞杆位置和位置指令在20Hz左右时达到了-90°的相位差,此时活塞位置相对于位置指令的衰减为50%,系统的截止频率在20Hz左右,表明仿真中的数字阀系统能够达到20Hz左右的带宽。对于数字式液压系统来说,动态性能较好。通过后续对系统控制算法进行优化,可以进一步提升系统的动态性能,提高数字阀系统在高频下的最优动态性能。
4 结 论
本文提出了一种新型的数字式电液作动器位置算法,搭建了双集成高速开关阀和阀控液压缸的数学模型,提出了一种查表形式的模型状态观测器,采用PWM和PNM协同的方式对作动器的位置进行控制。在Matlab和Amesim中搭建了仿真模型,根据火箭喷管上的作动器系统的真实参数设定了仿真参数,并进行了仿真验证。
仿真结果表明,对于幅值为100mm的正弦曲线,控制精度可达0.8mm,精度达到了0.8%。与此同时,系统的动态性能较好达到了20Hz。可见,数字式电液作动器的控制精度和动态性能都有较大提升,媲美比例伺服阀控制的作动器位置控制精度。
但是本文的流量-压力查询表格还存在精度较低的问题,可以通过进一步的实验及仿真提升表格精度,减小作动器位置跟踪误差;在进行仿真时,未考虑实际情况中管路的能量耗散以及效率等问题。在实际实验时所需开关阀数量要多于仿真,故需要在后续的实物样机实验中增加开关阀数量,对实际系统中所需的开关阀数量进行探讨,优化整个数字式电液作动器系统。下一步计划根据设计的模型研制数字式电液作动器样机,并通过开展实验对智能控制算法的效果进行验证。
