一种基于状态反馈的比例伺服阀控制方法*
2022-04-02方梓帆李海宾陈冬冬
仇 智,苏 琦,方梓帆,李海宾,陈冬冬,方 磊
(1.浙江大学 机械工程学院·杭州·310057;2.上海衡拓液压控制技术有限公司·上海·201612;3.内蒙古北方重工业集团有限公司·包头·014033)
0 引 言
随着液压系统在工程中的应用日益增多,对控制性能要求更高且期望控制方式简单有效,电液比例控制技术也因此得到应用。电液比例控制技术具有简化液压系统、控制精度高、抗污染性强和使用简便的优点。伺服阀极高的频响和控制性能对加工精度提出了很高的要求,同样要求很高的过滤精度,因此造价很高。然而,比例阀价格低廉,对加工精度和过滤精度要求低,具有很强的抗污染能力;但是频响相对较低,控制性能较差。比例伺服阀结合了伺服阀和比例阀的优势,性能优于比例阀,抗污染能力优于伺服阀,能够满足大多数高性能电液控制系统的应用需求。
在比例伺服阀的阀芯位移精确控制中,关键在于解决阀芯位移控制系统的非线性问题。比例伺服阀的非线性主要包含两方面:比例电磁铁及其驱动电路的非线性;阀芯上摩擦力液动力组合而成的阻力非线性。龚斌对比例电磁铁的静态特性进行仿真研究,采用有限元法分析工作气隙和锥面形状宽度对电磁力非线性的影响。徐兵等对反接卸荷式驱动电路建立非线性模型,重点描述占空比漂移、峰谷不对称、小占空比波形失真的非线性现象,并以此为指导进行控制器设计。陈立娟等指出,比例阀的电磁铁线圈电感为非线性,会导致高频响下的电流滞后,采用在线圈两端并联电阻和二极管的方式消除电感影响。SONG E.Z.等针对比例电磁铁非线性特性引起的滞后进行研究,通过对比例电磁铁执行器建模,采用一种基于神经网络的逆模型控制策略,对电磁铁进行线性化补偿,实验结果表明,该方法改善迟滞效果显著。PENG Z.等为解决工程中比例电磁铁强非线性导致的难分析建模问题,利用键合图的方法建立简化模型并做实验分析,结果证明该方法准确度很高,可以为比例电磁铁的电流和力控制提供依据。在液动力的研究方面,同样有很多学者做了仿真分析和实验验证。王建森等对非全圆周开口滑阀的稳态液动力进行数值计算,结果显示当阀口开度增大,液动力呈现先增后减的非线性趋势,出口压差和节流槽个数都会影响液动力数值。张宏等对大流量多路阀稳态液动力进行仿真分析,通过不同湍流模型计算稳态液动力,最终与实验结果和理论计算结果比对发现,稳态液动力同样有非线性结果,最高峰值达到140N。方锦辉等对比例伺服阀进行建模分析,并采用多项式拟合出液动力与阀芯位移关系,最终采用闭环PID验证模型的有效性。
在比例伺服阀的数字控制器中,由于存在上述系统非线性特性,使用传统PID控制算法时控制效果不理想,甚至容易出现闭环控制失稳。毛锐根据比例阀控液压缸系统的非线性特点,设计了静态和动态补偿算法,并将其应用于PID控制算法中,最终发现两者在取值合适的情况下都有良好的效果。高翔对电液比例加载系统进行建模和辨识,在传统PID实验效果不佳的情况下采用模糊PID控制,最终同样取得了良好的效果。汪亮培等以采煤机电液比例位置系统为对象建立相应的数学模型,将单神经元与PID相结合,在Simulink中进行仿真,得到了良好的控制效果,并发现单神经元自适应PID具有较强的鲁棒性。R.CAPACI 等为解决阀黏性阻尼导致的持续振荡问题,采用基于PID的声阻补偿技术,最终消除了黏性阻尼并实现了定点跟踪和干扰抑制。Y.R.KO等提出了一种用于电液比例阀的并联控制算法,该控制器包含一个前馈控制器和一个PID控制器,实验证明了该算法能够满足精确控制和高可靠性要求。
本文针对项目中的电液比例伺服换向阀进行高性能位置闭环控制算法研究,在研究分析控制系统的液动力和驱动力非线性特性的基础上,提出了一种位置负反馈式的PID控制,实验结果表明,该方法能够有效解决传统PID控制无法应对阀系统的非线性问题。
1 比例伺服换向阀中的非线性问题
1.1 比例伺服换向阀结构
本文比例伺服换向阀总体设计采用三位四通位移反馈式比例伺服换向阀,主要由电磁铁、滑阀组件、LVDT反馈组件等组成。其结构原理图如图1所示。比例阀的工作原理为:当电磁铁线圈输入控制电流,在衔铁上生成的控制磁通与永磁磁通相互作用,于是衔铁上产生一个力,促使衔铁、弹簧管、阀芯移动一个正比于控制电流的位移,阀芯运动直到位移反馈组件产生的信号与控制信号相等。此时,阀芯的位移与控制电流的大小成正比,阀的输出流量比例于控制电流。

图1 比例伺服换向阀结构原理图Fig.1 Structural schematic diagram of proportional servo directional valve
1.2 电磁铁位移—电流特性的非线性
在初步实验中,阀采用串级PID控制,电磁铁线圈电流通过PI控制器进行控制,形成串级控制的内环。阀芯运动部分通过PID控制器进行控制,形成串级控制的外环。在实验中测量开环电磁铁电流时发现,线圈电流与阀芯位移不成线性比例,图2所示为电磁铁位移—电流特性。

图2 电磁铁位移—电流特性Fig.2 Electromagnet displacement-current characteristics
从图2中可以看出,当阀芯正向位移大约为0.56mm时,电流达到峰值0.69A,随后电流随着阀芯位移增大而下降,呈现出非线性现象。当阀芯反向位移大约为0.83mm时,电流达到峰值0.7A,同样呈现出较强的非线性。这说明,虽然阻力中的弹簧力在随阀口开度而增大,但是液动力却在减小,导致两者的合力所平衡的电磁力减小。如果继续采用传统PID控制,在阀芯位移处于后半段时会出现严重的振荡现象,其本质是后半段阀芯位移与电流特性从正相关变为负相关,PID控制无法消除该非线性。
1.3 阀芯液动力的非线性
根据前文发现的电磁力非线性,需要研究系统中的非线性环节。由于电流环部分频响很高,接近为比例环节,因此不包含非线性。采用的电磁铁模型可以简化为一阶惯性模型,因此同样不存在非线性,最后通过分析阀芯受力可得非线性来自稳态液动力。为了仿真得到可靠的液动力数据,在Solidworks中建立阀芯阀套物理模型,然后在ANSYS中做前处理得到流体域模型,之后经过网格划分再使用Fluent进行仿真计算,使用滑移网格和设置壁面速度来批量仿真不同阀口开度下的流场特性,最后再根据后处理计算阀芯轴向受力得到稳态动力。图3所示为仿真得到的稳态液动力变化规律。

图3 稳态液动力变化规律Fig.3 Steady flow force variation law
从图3中可以看出,当阀芯位移达到0.8mm时,液动力也达到峰值,此后液动力迅速下降,将弹簧力和稳态液动力相结合后,和电磁铁的位移—电流特性变化趋势是吻合的。因此,可以判断引起电磁铁电流变化的主导因素即为稳态液动力的非线性特点,对于该现象同样需要针对性处理,以便PID能够较好地控制非线性系统。
2 数学模型的建立
2.1 物理模型数学建模
对于比例伺服换向阀的机械运动部分,其动力学模型如下
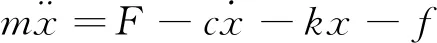
(1)
式中,为阀芯等运动组件质量;为阀芯位移;为电磁铁输出力;为黏性阻尼系数;为弹簧刚度;为液动力和摩擦力的合力。
可以通过仿真得到的数据进行拟合,表示成多项式的形式为
=+
(2)
式中,、为多项式系数。
对于电磁铁中的电路部分,线圈电流与电压可以简化为电阻和电感的串联
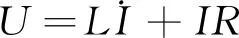
(3)
式中,为线圈电流;为输入线圈电压;为线圈电感;为线圈电阻。
电磁力和电流成正比
=
(4)
式中,为电流增益。
本文比例伺服阀电磁铁采用电压控制,由驱动电路不同占空比PWM输出控制电压的大小,占空比从控制器编程中计算得到,并作用于电流环输出,可得
=
(5)
式中,为位置环PID输出,即为占空比。
最终可得位置环PID输出至阀芯位移的微分方程为
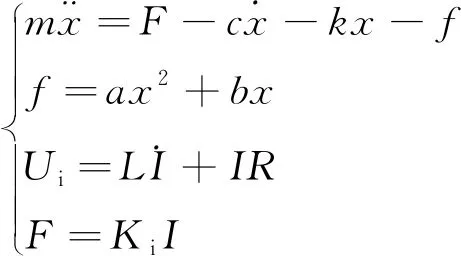
(6)
2.2 针对该系统改进的PID模型
传统PID的公式如下
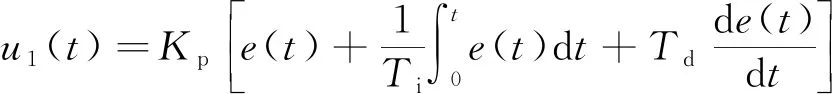
(7)
式中,()为传统PID控制器输出;为比例系数;()为此刻与上一时刻误差;为积分系数;为微分系数。
通过对系统进行初步调试,改进传统PID以尽量适配系统的非线性。由于整个系统采用了串级PID控制,在每一级PID输出后都加以限制,避免出现输出过大引起后项产生不必要的误差。首先对PID输出进行限幅:在位置环(外环)输出加入上下限,以限制输入给PWM驱动模块的占空比,具体公式如下

(8)
同时对电流环(内环)输出进行限幅:在电流环输出设置上下限,具体公式如下
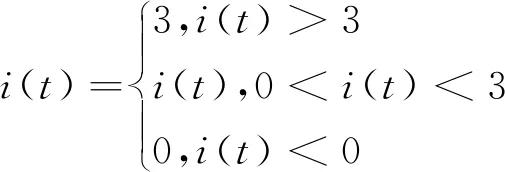
(9)
在阀控制中常常采用大阶跃信号,因此在跟随控制信号的过程中有较长时间存在大偏差。在外环对偏差进行限制,以保证积分输出不会出现饱和现象,具体公式如下

(10)
式中,()为目标值和实际反馈的偏差;为自行设定的误差上限;为自行设定的误差下限。
2.3 带有位置负反馈的PID模型
本文提出了带有位置负反馈的PID,实际上是除了零阶状态变量以外均为零的状态反馈。实验具体实现为:在线性区不对传统PID进行修改,但是保留改进PID的输出限幅和误差限幅设置,在非线性影响较大的区域采用折线进行位置反馈,以保证总输出呈现下降趋势,其中划分的区间个数、区间拐点和直线斜率均可通过调试获得,具体公式如下
()=()+()
(11)
(,)=
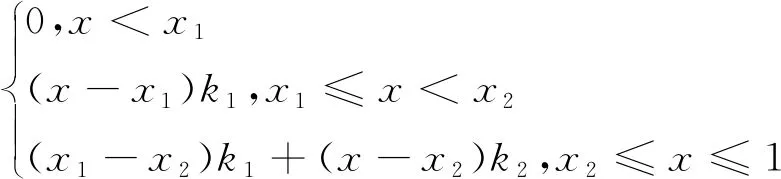
(12)
式中,()为采用状态反馈的补偿输出;为阀芯位移反馈;、为自行划分的拐点;、为自行设置的直线斜率。
根据微分方程建立整体系统框图,如图4所示。
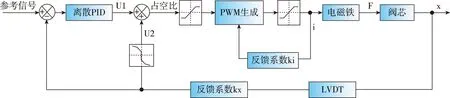
图4 整体系统框图Fig.4 Overall system block diagram
3 实验结果及分析
3.1 实验系统介绍
通过对带有位置负反馈的PID进行稳态和动态实验,观察其控制效果。稳态实验主要包含输入信号—流量实验。动态实验主要分为以下两部分:阶跃响应和频率响应。同时实验将改进PID算法与之比较,从而体现带位置负反馈PID算法的优势所在。实验是在浙江大学流体实验室进行的,采用的部分实验台液压原理图如图5所示。

图5 部分实验台液压原理图Fig.5 Hydraulic schematic diagram of partial test bench
各液压元件的规格如表1所示。

表1 各液压元件的规格Tab.1 Specifications of each hydraulic element
由电机带动变量泵供油,泵出口设置了高压滤油器,如此可以给被试阀提供可变流量,泵出口的溢流阀可以设定被试阀进口压力,被试阀负载可以通过连接A和B负载口的节流阀调节,油路中的压力和流量均可以从实验台中获得。
实验中的控制器为实验室自行开发的数字控制器,通过板载的PWM驱动部分输出±24V电压,同时控制器集成LVDT调理电路采集阀芯位移信号,进而控制电磁铁运动。在控制器外部使用16位高精度NI采集卡获得输入信号和LVDT的位移反馈信号,对最终获得的数据再进一步滤波处理得出对比结果。整个实验台及控制部分实物如图6所示。

(a)实验台实物图 (b)控制器实物图图6 实验台及控制部分实物Fig.6 Physical object of test bench and partial control part
3.2 稳态特性
根据实验测量改进PID算法的稳态特性,即为输入信号—流量关系,输入信号±10V和阀芯位移±1mm线性对应。在液动力线性区域改进PID算法控制稳定,但是当输入信号达到7.2V时(即为满输入信号+72%),阀芯位移出现波动,并且波动随着输入信号的增大变得更加剧烈,如图7所示。
(a)+72%满输入信号阀芯位移变化图
由此可见,即使是在稳态情况下,改进PID算法仍难以应对非线性液动力造成的影响,出现该现象的节点大约为输入信号7V,阀芯位移0.7mm处。但是通过加入位置负反馈,系统可以稳定。图8所示为带有位置反馈PID算法下的输入信号—流量特性。
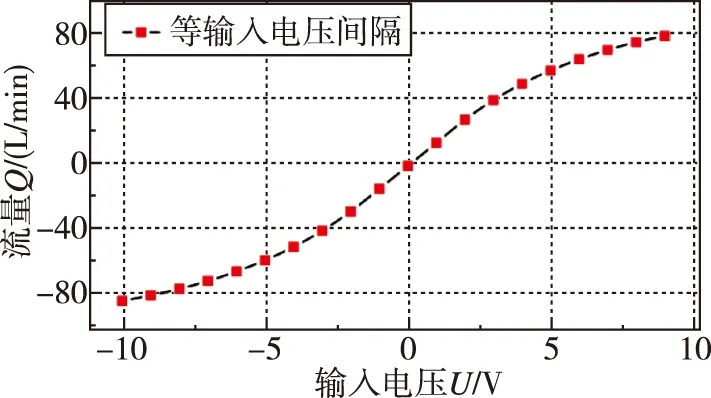
图8 带有位置负反馈PID算法下的输入信号—流量特性Fig.8 Input signal-flow characteristics under PID algorithm with position negative feedback
从图8中可以看出,当加入位置负反馈后,阀流量输出稳定,并且流量和阀芯位移呈正相关,满足了比例伺服阀的使用要求。
3.3 阶跃响应
为了检验该算法的动态特性,采用频率1Hz幅值9V阶跃观测带有位置负反馈PID响应,如图9所示。

(a)带位置负反馈PID算法负向阶跃
从图9中可以看出,在阀芯开启的过程中,即为输入信号幅值增大时,带有位置负反馈的PID快速响应基本无超调,负方向下降响应时间为20ms,正方向上升时间大约12ms,同时阀芯在阶跃最远位移回归至零位时的超调量同样很小。然而,改进PID无法控制该非线性区域,其响应结果如图10所示。

(a)改进PID较大参数阶跃响应
经过多次调整,仍无法寻找到合适的参数使得改进PID在非线性区域稳定,但是在线性区域改进PID能够实现有效控制。为了验证带位置反馈PID算法在改进PID控制效果较好的线性区域同样拥有出色的控制效果,采用频率1Hz幅值7V的阶跃信号对改进PID算法和带位置负反馈PID算法进行对比。根据前述实验结果,7V为改进PID的临界稳定点,因此既可以观测出改进PID的非线性临界特性,还可以表现出带位置负反馈PID的优越性,这里仅采用正向阶跃进行比较,响应结果如图11所示。

(a)改进PID算法阶跃
3.4 频率响应
采用对两种算法各自适合的PID参数,在不同频率正弦信号输入下的改进PID(算法1)和带有位置负反馈PID(算法2)的频率响应如图12所示。
三种输入信号幅值情况下的穿越频率和截止频率如表2所示。

(a)改进PID算法90%幅值频响
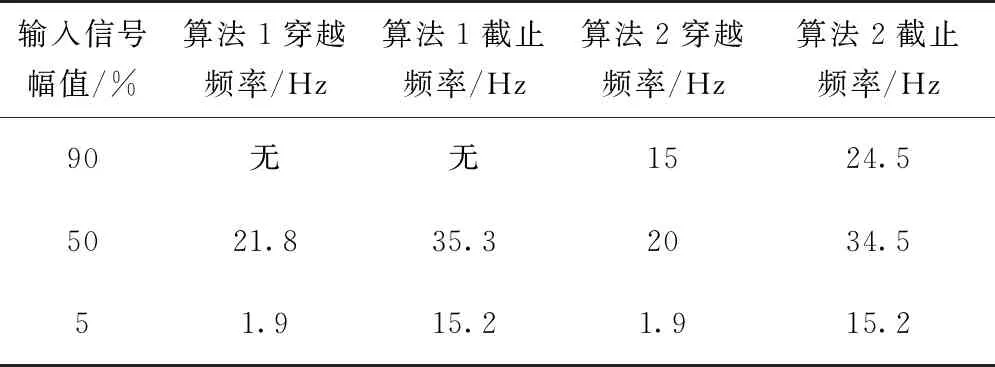
表2 三种输入信号幅值下频率对比Tab.2 Frequency comparison under three input signal amplitudes
首先,对于90%幅值的频率响应,改进PID算法基本很难控制,由上文中阶跃响应可以看出,系统出现严重的振荡现象,并且屡次达到机械上的限位值,造成电磁铁吸合。而当频率高于10Hz时,频率响应图中的幅值会有所上涨也是由于此原因,即为电磁铁吸合造成。时域响应曲线如图13所示。

图13 改进PID算法90%幅值正弦信号响应Fig.13 90% amplitude sinusoidal signal response of improved PID algorithm
带位置负反馈PID算法90%幅值的截止频率大约为24.5Hz。此外,由于90%幅值的频率响应过于激烈,因此决定采用较小的不同幅值对2个算法进行比较。对于50%幅值的频率响应,二者没有太明显的区别。改进PID有小幅度的幅值增大,这是因为没有位置反馈使得改进PID的输出大于实际需要,对目标信号的响应无法做到及时刹车,因此总会超出目标幅值(50%),但是在20Hz之后也会衰减,因此带位置负反馈PID的穿越频率和截止频率相对改进PID都稍微大一些,而两者相角响应基本一致。对于5%幅值的频率响应,二者同样没有太明显的区别,这是因为在这个线性区间内改进PID和带位置负反馈PID都有良好的控制效果,两者相角响应基本一致。
4 结 论
为了解决传统PID难以应对比例伺服阀中非线性液动力的问题,本文研究了一种基于状态反馈的比例伺服换向阀的控制方法:在传统PID的基础上加入适应实验系统的限制以改进算法,同时加入位置反馈来抵消非线性液动力,进而使PID充分发挥控制线性系统的良好效果,之后通过建模分析了加入位置反馈后系统能保持稳定。最后通过实验验证了该控制方法的有效性:
1)稳态特性良好,能保证输入信号和流量正相关。
2)阀口开度增大,阶跃响应几乎无超调,最大响应时间20ms,最小响应时间12ms。
3)对于幅值90%的频率响应,带位置负反馈的PID算法优于改进PID,能够有效遏制阀芯超调造成的电磁铁吸合;对于幅值50%和5%的频率响应,二者没有太大区别,这源于PID对线性区域的良好控制性能。
本文考虑非线性问题时集中于稳态液动力,对于电磁铁及其驱动电路部分的非线性进行了简化,另外阀芯的阻力部分包含摩擦力和瞬态液动力,这些因素均未考虑在内。在后续研究中应强化液动力、比例电磁铁的非线性建模和辨识,并将获取的结果应用于控制策略设计。
