2021年高考全国乙卷理科第19题的探究与启示

■ 哈尔滨师范大学 孔繁雪

近年来,高考对于数列的考察主要集中在等差数列、等比数列的证明及求和上,2021年全国乙卷的考察也将重点放在等差数列的证明及求和上,但相较于之前的注重对证明及求和方法的考察,乙卷的数列题更加注重学生对于基础知识的掌握以及对题目的理解,并且此次考试将数列题放在第19题的位置上,更加体现了对数列基础知识的重视。

1 试题呈现

题目(2021年全国乙卷19题)记Sn为数列{an}的前n项和,bn为数列{Sn}的前n项积,已知。

证明:(1)数列{bn}是等差数列;

(2)求{an}的通项公式。

2 试题分析

本题以bn与数列{Sn}之间的关系作为载体,主要考查数列通项an与数列前n项和Sn之间的关系及等差数列的证明,考查学生的推理论证及运算求解能力、考查分类与整合、特殊与一般、考查逻辑推理、数学运算等核心素养。

本题只需要准确bn与数列{Sn}之间的关系及具体的表示,并准确表示出n的范围,值得注意的是,n的范围所对应的通项公式也不一定相同,需要对首项进行检验。然后类比an与数列前n项和Sn之间的关系从bn与数列{Sn}之间的关系中得到Sn的通项公式,最终得到an的通项公式。

3 解法分析

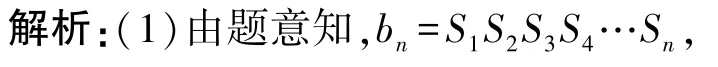
点评:

对于本题来说,难点在于正确理解bn为数列{Sn}的前n项积的含义,并将其和an与Sn之间的关系建立联系,然后准确地对式子进行变形、整理,值得注意的是,在计算第n-1项时n的范围是n≥2,并且需要将等差数列的首项计算出来,将首项进行检验看是否满足通项公式。第二问先是利用Sn与bn的关系计算出bn,再利用an与Sn的关系计算出an,并注意n的范围。通过对本题的求解,主要可以培养学生的类比以及分类讨论的思想,提高学生的逻辑推理能力。

4 高考题对比

点评:

这两道高考题的第二问都是在第一问求得了{an}的通项公式的基础上,利用前n项和的求和公式及其他方法求得Sn的,主要考查学生的逻辑思维能力、运算求解能力、转换思想等。

这两道高考题与全国乙卷的高考题相比,全国乙卷的解题程序与此相反,已知{Sn}前n项积,得到Sn的通项公式,再通过an与Sn之间的关系,最终得到an的通项公式,弱化了对技巧以及方法的考察,着重考查学生的基础知识及其阅读理解能力。

5 启示与建议

5.1 落实“双基”

俗话说,基础不牢,地动山摇。考试的重点在于学生所表现出来的基本知识和基本方法,并在此基础上考查学生的基本技能。因此,在教学过程中,教师应注意对基础知识本质的剖析,注重学生对于基础知识和基本技能的学习与理解,在教学过程中放缓教学速度,循序渐进,稳扎稳打,这是解决数学问题的前提,也是学生提高学生数学能力的基石,是提高数学核心素养的保证。

5.2 注重通性通法

如今的高考题特别注重考查通性通法,淡化特殊技巧。因此,在复习中要注意对基本方法、典型思想的培养,对于一些华丽但并不实用的方法并不提倡学生使用,应追求具有思想价值及通用的方法。应注重对于通性通法的练习,以提高解题能力。

5.3 回归教材

注意回归教材本源,选择有针对性的问题,对基础知识、基本方法进行巩固提升,确保每块内容的基础得到真正落实,从而进行灵活应用,有效切实提高学生解题能力。

5.4 促进深度学习

深度学习被认为是实现核心素养落地的重要途径,因此,在进行学习及复习时应注重学生的接受程度以及心理发展规律,教学不宜过快,应让学生慢慢思考,引导学生在解决问题的同时注意培养学生自我反思解题及方法的习惯,重视对知识的本质的挖掘与理解,促进学生对问题的深度与广度的认识,增强学生解决问题的能力。

5.5 类比学习,举一反三

不难发现,高考对于数列的考察主要集中在基础知识及基本内容的变形等,因此,学生应注重对课本知识的理解与运用,以及应具备将书本上的基础知识迁移的能力,学会类比学习,就举一反三,以加深学生对于知识的理解,提高学生解决问题的能力以及发展学生的数学核心素养。