以“双曲线标准方程”为例探讨数学核心素养的培养

■ 无锡旅游商贸高等职业技术学校 赵沙沙

1 在GeoGebra绘图过程中培养学生直观想象核心素养

信息技术的发展带动了各个领域的进步,也为现代职业学校教学提供了很多选择。特别在圆锥曲线章节,利用信息技术为平台,为学生演示各曲线的形成过程,使教学方式丰富多样,增强学生对圆锥曲线的直观理解,便于培养学生直观想象的数学素养。

在讲解双曲线定义之前,给学生演示何种曲线是双曲线,条件允许的话,可以请同学们打开GeoGebra软件,跟随老师一起演示双曲线的形成过程。打开GeoGebra软件,输入指令:

各指令表示的意思分别是:左焦点;右焦点;构造圆;控制圆上的点A;圆上一点A;使即定值,且A动则M动;

显示线段MF_1;显示线段MF_2;显示文本;显示双曲线。

学生只需要把指令输入到GeoGebra中,拉动滑动条,即可显示双曲线的形成过程,即“平面内与两个定点的距离的差的绝对值等于非零常数(小于两定点距离)的点的轨迹叫作双曲线。”GeoGebra软件作图,让双曲线这一抽象的定义生动形象,学生在直观感受中领会双曲线的概念,加强自身的直观想象素养。

2 在标准方程推导过程中培养学生数学运算、逻辑推理核心素养

双曲线的标准方程在双曲线一节中占有重要地位。推导双曲线标准方程的第一步,是建立适当的直角坐标系。通过小组内部交流合作,每个人都有可能提出不同的建立坐标系的方案,有的小组会以双曲线焦点所在直线为y轴,其垂直平分线为x轴建立直角坐标系;有的小组会以双曲线两焦点之一为原点建立直角坐标系;有的小组会以双曲线焦点所在直线为x轴,其垂直平分线为y轴建立直角坐标系。每一个建系方案都蕴藏着学生对双曲线定义的自我理解和逻辑推导,理论上都是可行的,只是推导标准方程的计算量和最终得到的方程会有差异。

若以双曲线焦点所在直线为x轴,其垂直平分线为y轴建立直角坐标系,根据焦距为2c,即可得到两焦点的坐标分别是(-c,0)、(c,0),这样就完成了第二步设点,这一步骤学生可以在教师的问题指引下得出。依据双曲线的定义,双曲线上任一点(x,y)到两焦点距离差的绝对值是常数2a,结合两点间的距离公式,可用提问的方式得出第三步列式,得到:

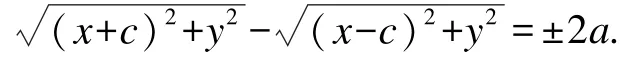
第四步的化简过程尤其考验学生的数学运算和逻辑推理能力:移项,得

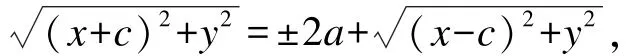
两边同时平方并化简,得:

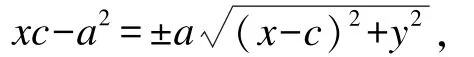
两边再同时平方,然后两边同时除以a2(c2-a2),

令c2-a2=b2(b＞0),得:

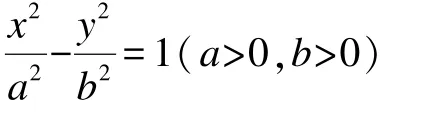
这样就得到了焦点在x轴的双曲线的标准方程。带根式方程的化简通常会应用平方,对所列式子先移项再平方是简化计算过程的技巧,化简过程用到两次平方,对学生的计算能力是一大挑战。

推导双曲线标准方程用到的四个步骤:建系、设点、列式、化简,是一个层层递进,环环相扣的过程。每个曲线方程的推导都能用到这几个步骤,十分考验学生的逻辑推理能力和计算化简能力。

3 在实际问题解决过程中培养学生数学建模核心素养

职业院校以培养专业技术型人才为定位,很多专业十分注重实践性。对部分同学来说,学习抽象数学的过程是鲜有乐趣的,甚至会有人怀疑自己学习数学的意义,因此有“数学无用论”出现。利用数学建模思想将实际问题转化为数学问题很好地改善了这一情况,教师可以通过数学建模帮助学生提高数学核心素养,引导学生积极思考、探索、解决问题。

在双曲线应用一节中,针对酒店管理专业的学生,我们可以设计问题:为规划餐车运行路线,酒店经理碰到一个难题,他将这一问题与职校毕业的小陈一起商量,也就有了下面的研究:如图,酒店餐车在M处,需要沿路线MA或MB送到ABCD中去,经测量知MA=40米,MB=60米,∠AMB=60°,能否制定一个运送方案,使运送距离最近?

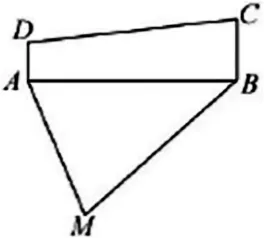
图1 建模例图(一)

数学建模思想解决实际问题的实质是“读懂实际问题、建立相应模型”。我们首先得分析清楚题中的已知与未知,理顺题中已知和未知之间的关联,进而选择合适的模型。在这道餐车路径规划的实例中,我们首先将实际问题转化成数学问题,建立坐标系,将各区域边界点在坐标系中,将已知条件转换求解。餐车路径规划可以分成三组情况:(1)沿MA运送最近;(2)沿MB运送最近;(3)沿MA和MB运送一样近。假设方案三成立,那么对界限上的任意一点P,恒成立,即是一个定值,并且,根据双曲线的定义知,这个界限的轨迹是双曲线的其中一支。

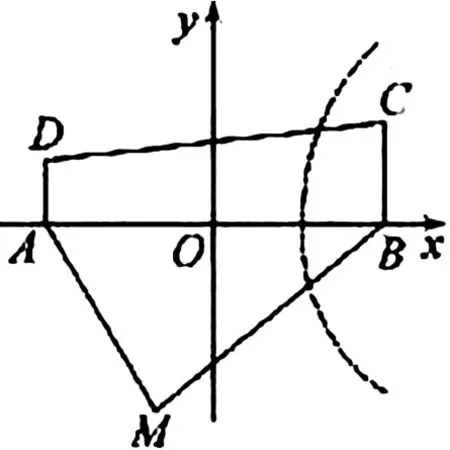
图2 建模例图(二)

从而我们可以以AB所在直线为x轴,其垂直平分线为y轴建立直角坐标系。设双曲线方程为:

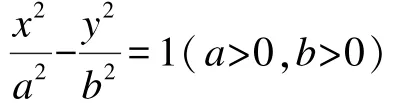
读懂题意,建立模型是解决问题的难点,特别是建立模型,需要通过训练增强数学建模素养。

第二步是“分析条件找点,代入求出方程”,问题中已经转换的点坐标和按题意设立的方程模型需要进一步“反应”,进而催化出所需的方程式。这一步是解决问题的关键,起到承上启下的作用,“点”找对了,“方程”才能求对。而在此过程中,需要同学们具备一定的数学计算能力。在这个实例中,我们利用余弦定理求出AB的长度,进而求出焦点A、B的坐标,最后求解出双曲线方程:

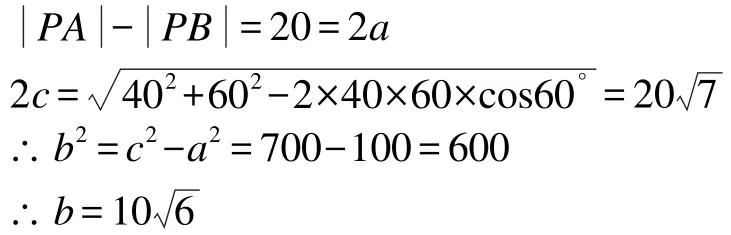
最后一步是“还原具体情况,解决实际问题”,数学模型解开了,数学问题解决了,最终还需还原至实际问题。这一步是问题解决的终点,也是解决问题的收官之处。在此过程中,要切实做到如实还原,不遗漏、不繁琐。在这道餐车路径规划实例中,求出右支双曲线方程后,一定要还原至实际问题就是当运送到界限左边时,沿MA运送较好;当运送到界限右边时,沿MB运送较好;当运送到界限上的地方时,沿MA、MB一样。

数学建模在数学课堂上的有效应用,可以让学生体会到学习数学的快乐和实用性,在解决问题的过程中,学生在学习过程中处于主体地位;在数学模型求解过程中,需要学生对基础知识掌握扎实,同时需要具备较强的运算能力。有效的数学建模课堂是培养学生数学核心素养的高效途径。

圆锥曲线作为职业学校数学教学的重点内容,是平面解析几何知识的继续学习,其蕴含的知识点美丽又抽象,缜密而细致。教师可以通过与专业相结合加强知识的趣味性,例如在讲解双曲线一节时,可以从专业中的曲线美、生活中的曲线美入手,通过展示学生搜集的带有三类圆锥曲线的专业设计图片等实现德育渗透,落实课程目标立德树人的根本任务。作为一个生动的知识引导者,教师也可以通过增设数学实验环节加强课堂的生动性。例如在讲解双曲线一节时,可以通过手工折纸等方式折出双曲线,使学生领会双曲线定义的精确性;可以将课堂搬到车间厂房,通过观看不同数据对机器产生的影响,使学生领会数据准确性的重要意义。

数学学科的六个核心素养作为学科育人的价值集中体现,是培养人才、践行社会主义核心价值观的重要载体。教师在教书育人过程中,要常思考多尝试,用高效的方式践行“立德树人”之本、培养强国之才。