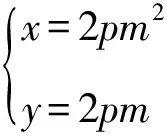直线的参数方程在解析几何竞赛题中的应用
2022-04-01贺航飞
数理化解题研究 2022年7期
贺航飞
(海南省海南中学 571158)
基金项目:海南省教育科学“十三五”规划立项课题“基于智慧课堂的理科资优生培养校本课程体系构建”基于智慧课堂的理科资优生培养校本课程体系构建(项目编号:QJY20191035).
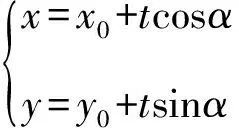
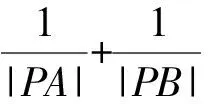
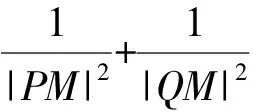
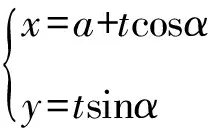
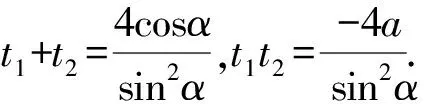
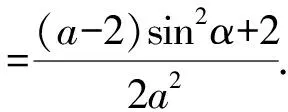
由于a为常数,上式取值要跟α无关,当且仅当a-2=0,即a=2.
评注像这种只涉及到长度计算的题型就能充分体现直线参数方程的优越性,相对于传统方法,计算量大大减小. 需要注意的是,相关点要在同一直线上.
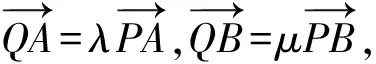
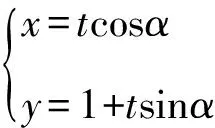
联立,得t2+2tsinα-3=0.
A,B对应的参数t1,t2是以上方程的两根,
则t1+t2=-2sinα,t1t2=-3.
点P对应的参数tP=0,令y=0,
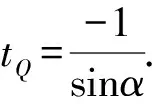

评注在直线的参数方程中,只要知道点的横坐标或者纵坐标即可求得此点对应的参数. 由于t的几何意义是有向距离,在计算相关长度时要带有绝对值,再结合具体条件考查能否去掉绝对值.
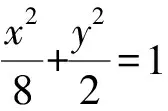
解析|AC|2<|CD||CB|,下面给出证明.
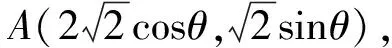
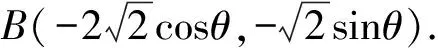
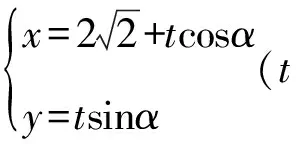
其中θ,α均是锐角.
=6cos2θ-16cosθ+10
=(1-cosθ)(10-6cosθ).

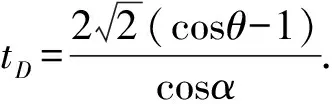
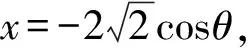
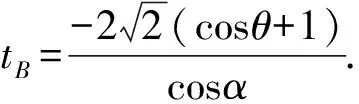
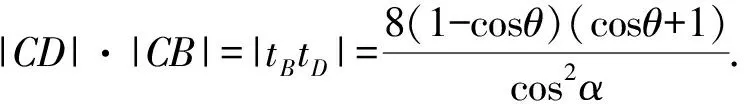
直线BC的斜率
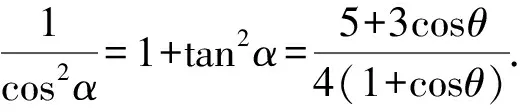
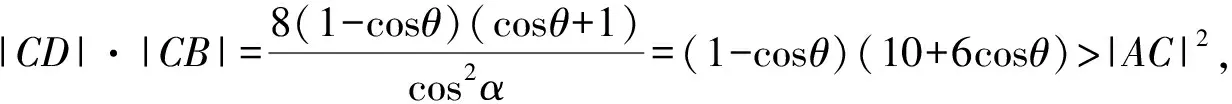
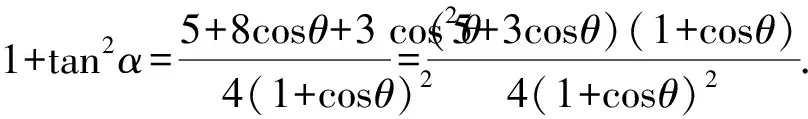
例4 (2017年全国联赛B卷)在平面直线坐标系xOy中,曲线C1:y2=4x,曲线C2:(x-4)2+y2=8. 经过C1上一点P作一条倾斜角为45°的直线l,与C2交于不同的点Q,R,求|PQ||PR|的取值范围.
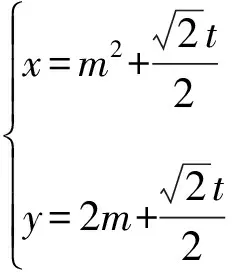
点Q,R对应的参数t1,t2是以上方程的两根,
则|PQ|·|PR|=|t1t2|=m4-4m2+8=(m2-2)2+4.
=-2m(m-4)(m+2)(m-2)>0,
解得m∈(-2,0)∪(2,4),此时m2-2∈
(-2,2)∪(2,14).
从而|PQ|·|PR|=(m2-2)2+4∈[4,8)∪(8,200).