利用斯特瓦尔特定理解答2021年的几道高考试题

董立伟

(山西省太原市第三实验中学校 030031)

基金项目：太原市第六届教师个人课题“基于学生深度学习的高中生数学阅读能力的培养研究”(项目编号：GR-21469).

斯特瓦尔特定理：设P为△ABC的BC边上任一点(P≠B，P≠C)，则有

利用余弦定理可以很容易地给出斯特瓦尔特定理的证明，此处不再赘述.

以下我们利用斯特瓦尔特定理解答几道2021年的高考试题.

A. 13 B. 12 C. 9 D. 6

解析由斯特瓦尔特定理，得

因为O为线段F1F2的中点及

配方，得

(MF1+MF2)2-2MF1·MF2=2MO2+10.

将MF1+MF2=6代入并化简变形可得

MF1·MF2=13-MO2.

设M(x0,y0)，由点M在椭圆C上可得

所以MF1·MF2=13-MO2

当且仅当x0=0时等号成立.

所以|MF1|·|MF2|的最大值为9.

故选C.

例2 (2021年新高考Ⅰ卷第19题)记△ABC的内角A,B,C的对边分别为a,b,c.已知b2=ac，点D在边AC上，BDsin∠ABC=asinC.

(1)证明：BD=b.

(2)若AD=2DC，求cos∠ABC.

解析(1)由BDsin∠ABC=asinC及正弦定理，得

(2)由斯特瓦尔特定理，得

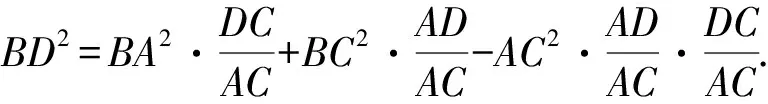
由BD=b及AD=2DC，得

化简变形，得

11b2=6a2+3c2.

因为b2=ac，

所以6a2-11ac+3c2=0.

即(3a-c)(2a-3c)=0.

当c=3a时，b2=3a2.

由余弦定理，得

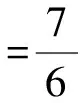
由余弦定理，得

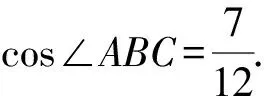
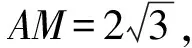
解析由斯特瓦尔特定理，得

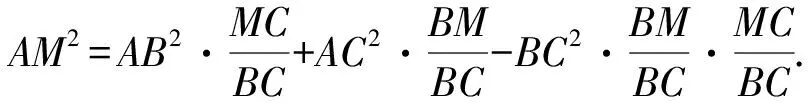
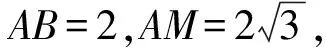
在△ABC中对∠B用余弦定理，得

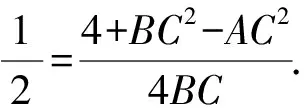
BC2-4BC-32=0.

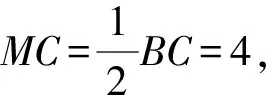
并在△MAC中对∠MAC用余弦定理，得