基于权重配置的多环路COT控制Buck变换器瞬态性能优化
2022-04-01张中伟王天石曲小慧
张 希, 张中伟, 王天石, 曲小慧
(1. 东南大学电气工程学院, 江苏 南京 210096; 2.常州大学微电子与控制工程学院, 江苏 常州 213164)
1 引言
由于大部分时间工作在休眠模式,微处理器等负载要求为其供电的电压调节器具有高轻载效率[1]。恒定导通时间(Constant On-Time, COT)是一种变频控制技术,与定频控制技术[2]相比,具有更高的轻载效率,因而更适合应用于微处理器等负载的电压调节器中[3-6]。
电流型COT控制[7]和V2-COT控制[8]是两种应用非常广泛的双环COT控制。电流型COT控制采样电感电流信号作为控制内环反馈信号,具有限流和均流等功能,但负载瞬态性能较差[7];V2-COT控制利用输出电容等效串联电阻(Equivalent Series Resistance, ESR)采样电容电流信号作为控制内环反馈信号,具有负载瞬态响应速度快等优点,但其控制性能依赖输出电容ESR,且无法实现限流[8]。为此,文献[9]通过在控制内环引入电感电流权重和输出电压权重提出了一种多环路COT控制技术,并研究了小输出电容ESR情况下权重配置对Buck变换器稳定性的影响。
然而,小输出电容ESR情况下电感电流和输出电压在控制内环的权重不仅影响变换器的稳定性还影响其瞬态性能。为此,本文将研究权重配置对瞬态性能的影响,并给出优化瞬态性能的权重配置策略。
2 多环路COT控制Buck变换器
2.1 工作原理
多环路COT控制Buck变换器的原理图和主要稳态工作波形如图1(a)和图1(b)所示[9]。其中,Kc和Kv分别为电感电流iL和输出电压vo的采样系数;Rc和Rv分别为iL和vo的权重电阻,用于配置电感电流和输出电压在控制内环反馈信号vsum中的权重;电压补偿环路由反馈增益g和时间常数τ的比例积分(Proportional Integral, PI)补偿器构成,g=Ra/Rin,τ=RaCa。
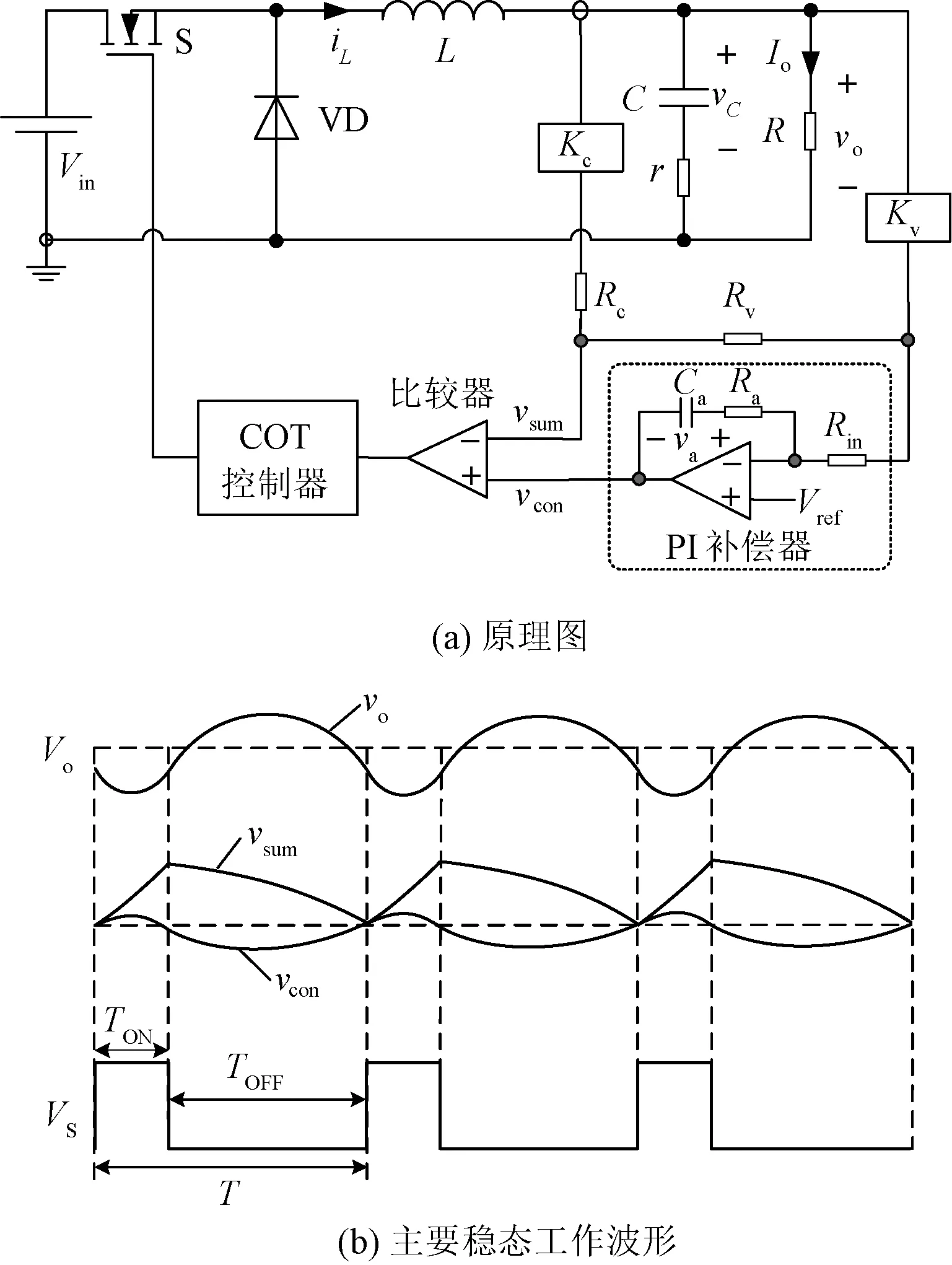
图1 多环路COT控制Buck变换器Fig.1 Multi-loop COT controlled Buck converter
根据叠加定理,控制内环中电感电流权重ωc和输出电压权重ωv分别可以写成[2]:
(1)
由式(1)知,ωc、ωv满足0≤ωc≤1、0≤ωv≤1且ωc+ωv=1。
从图1(a)可以看出,开关管S导通后,控制内环总的反馈信号vsum开始上升;当达到导通固定时间TON后,开关管S关断,vsum开始下降,当vsum下降到vcon时,开关管S再次导通,进入到下一个开关周期。图1(b)中,Vo为输出电压平均值;VS为控制脉冲。
2.2 不同权重配置的瞬态性能分析
为了直观展示不同权重配置对多环路COT控制Buck变换器瞬态性能的影响,采用表1的典型电路参数进行PSIM电路仿真。当负载电流Io从5 A跳变到7 A再跳回到5 A时,多环路COT控制Buck变换器在权重配置为(ωc,ωv)=(0.6, 0.4)和(0.4, 0.6)时的输出电压波形如图2所示。
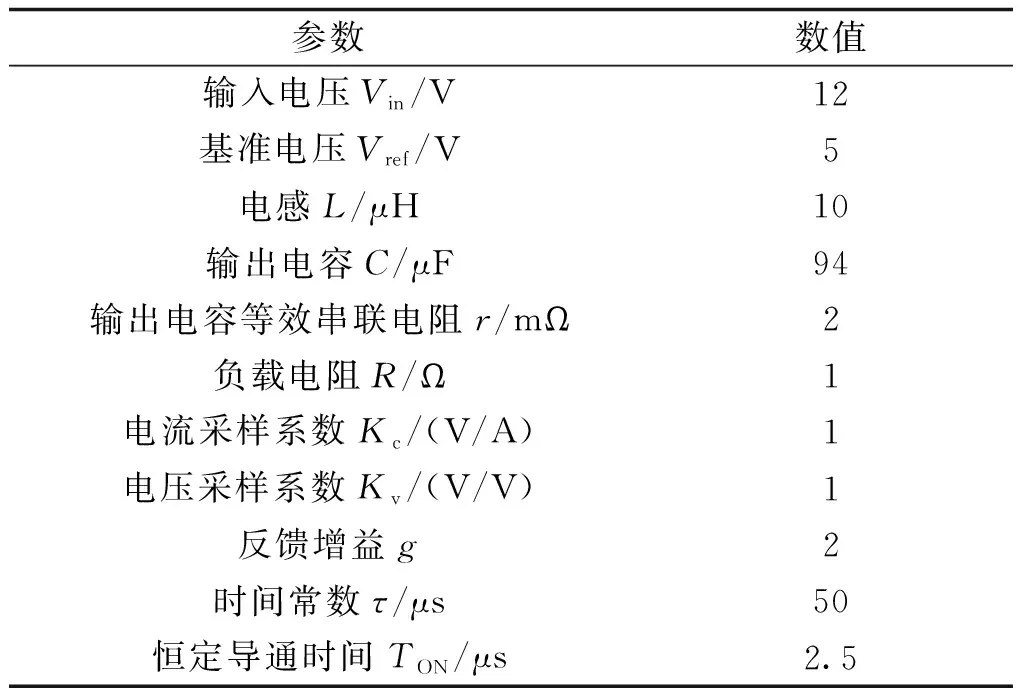
表1 多环路COT控制Buck变换器的电路参数Tab.1 Circuit parameters for multi-loop COT controlled Buck converter
图2中,权重配置为(ωc,ωv)=(0.6, 0.4)和(0.4, 0.6)时,多环路COT控制Buck变换器的恢复时间基本相同,但前者的输出电压下冲量和上冲量明显大于后者。这表明减小电感电流权重(或增大输出电压权重)可以提高多环路COT控制Buck变换器的瞬态性能。然而,由文献[9]可知,当电感电流权重过小(或输出电压权重过大)时,多环路COT控制Buck变换器将工作在不稳定状态。因此,为了优化多环路COT控制Buck变换器的瞬态性能,有必要研究权重配置策略。
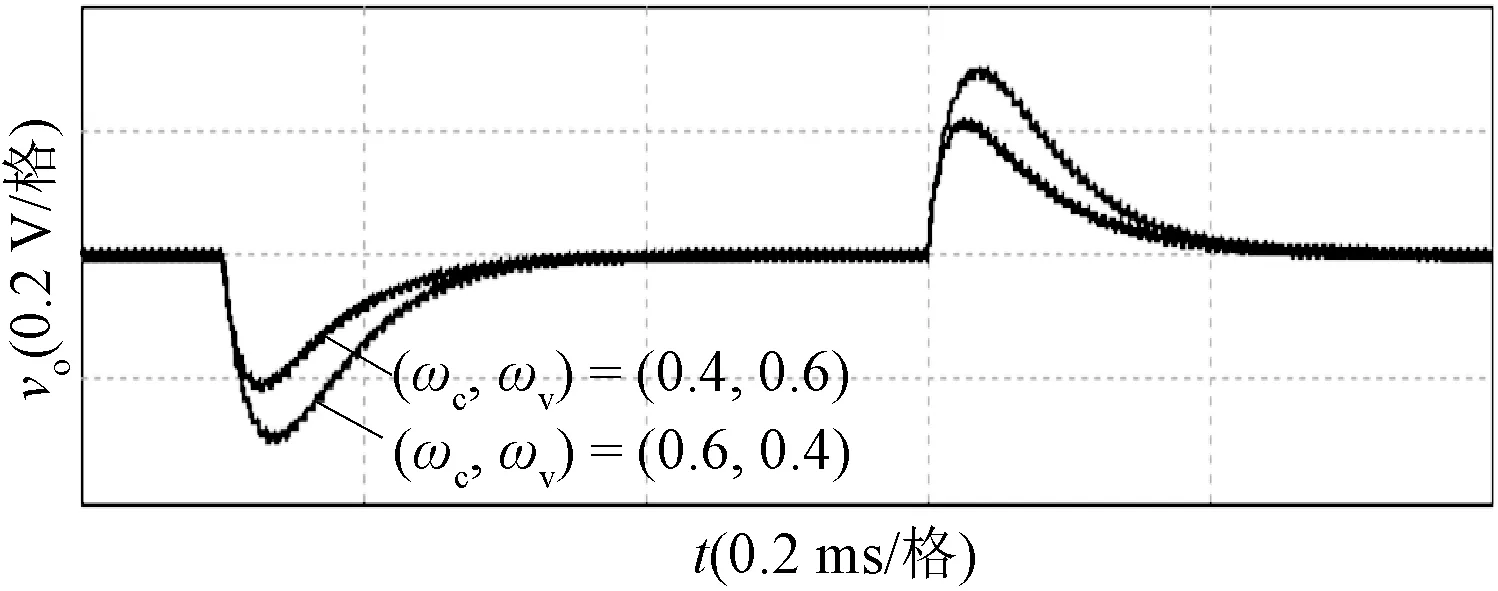
图2 两种权重配置时输出电压的仿真结果Fig.2 Simulation results of output voltage under two weight configurations
3 基于权重配置的瞬态性能优化
本节将先从负载加载和减载两种情况进行分析,进而讨论优化多环路COT控制Buck变换器瞬态性能的权重配置策略。负载跳变点(即负载跳变发生时刻)影响开关变换器的负载瞬态响应速度[8]。负载跳变量相同时,开关变换器在最坏负载跳变点发生跳变将具有最大的偏移量和最长的恢复时间,即瞬态性能最差。为了使研究内容可以涵盖所有情况,本文选择最坏负载跳变点进行研究。
需要说明的是,根据ωc和ωv之间的约束关系(即ωc+ωv=1),若确定了ωc,则ωv相应确定。
3.1 优化负载加载瞬态性能的权重配置
在开关管关断时间结束时刻,电感电流处于谷值,电感储存的能量最少,此时负载加载所产生的下冲量最大,所需要的恢复时间最长,故关断时间结束时刻是最坏负载加载点。
根据多环路COT控制Buck变换器的工作原理可知,若负载在最坏加载点加载,实现最优瞬态性能的理想瞬态过程为:经过一个导通时间ton(ton为TON的整数倍)和一个关断时间toff后,电感电流刚好进入到新的稳态。图3给出了该瞬态过程输出电容电流iC和输出电容电压vC的波形示意图。需要说明的是,本文的最优瞬态性能是指其他电路参数给定后,通过配置电感电流和输出电压权重实现的最佳瞬态性能。相较于其他权重配置,采用该权重配置时变换器不存在欠阻尼振荡且过冲量最小、恢复时间最短。

图3 最坏负载加载点的理想瞬态过程Fig.3 Ideal transient process at the worst load step-up point
在图3中,负载电流Io在t=t0处发生跳变,跳变量为ΔIo,up。由于在Buck变换器中,输出电容电流iC等于电感电流iL与输出电流Io之差,即iC=iL-Io,且iL无法突变,故该跳变量立即反映在电容电流上。在随后的瞬态过程中,iC和vC的变化如下:iC从谷值iC=-ΔIo,up-0.5ΔiC处开始上升,上升斜率为m1=(Vin-Vo)/L,其中Vin、Vo和L分别为输入电压、平均输出电压和电感,同时输出电容开始放电,vC下降;t=t1时,iC=0 A(即iL=Io),vC具有最大下冲量,同时输出电容开始充电,vC开始上升;t=t2时,iC上升到峰值IP,开关管S关断,iC开始下降,下降斜率为m2=Vo/L;t=t3时,iC下降到0 A,输出电容开始放电;t=t4时,iC进入新稳态(即电感电流进入新稳态),此时iC=-0.5ΔiC。根据电容电荷平衡原理可得,在电容电流瞬态过程中,负载加载从输出电容中抽走的电荷Qex等于输出电容放电电荷(Q1+Q3)与充电电荷Q2之差,即:
Qex=Q1+Q3-Q2
(2)
其中
由式(2)可求得该理想瞬态过程中输出电容电流的峰值IP。然而,在多环路COT控制Buck变换器的实际工作过程中,如图3所示的理想瞬态过程往往无法满足。在实际工作中,负载在最坏加载点加载时,实现最优瞬态性能的实际瞬态过程为:电感电流经过两个导通时间和两个关断时间后进入到新稳态[8]。此时,输出电容电流iC的波形示意图如图4所示。
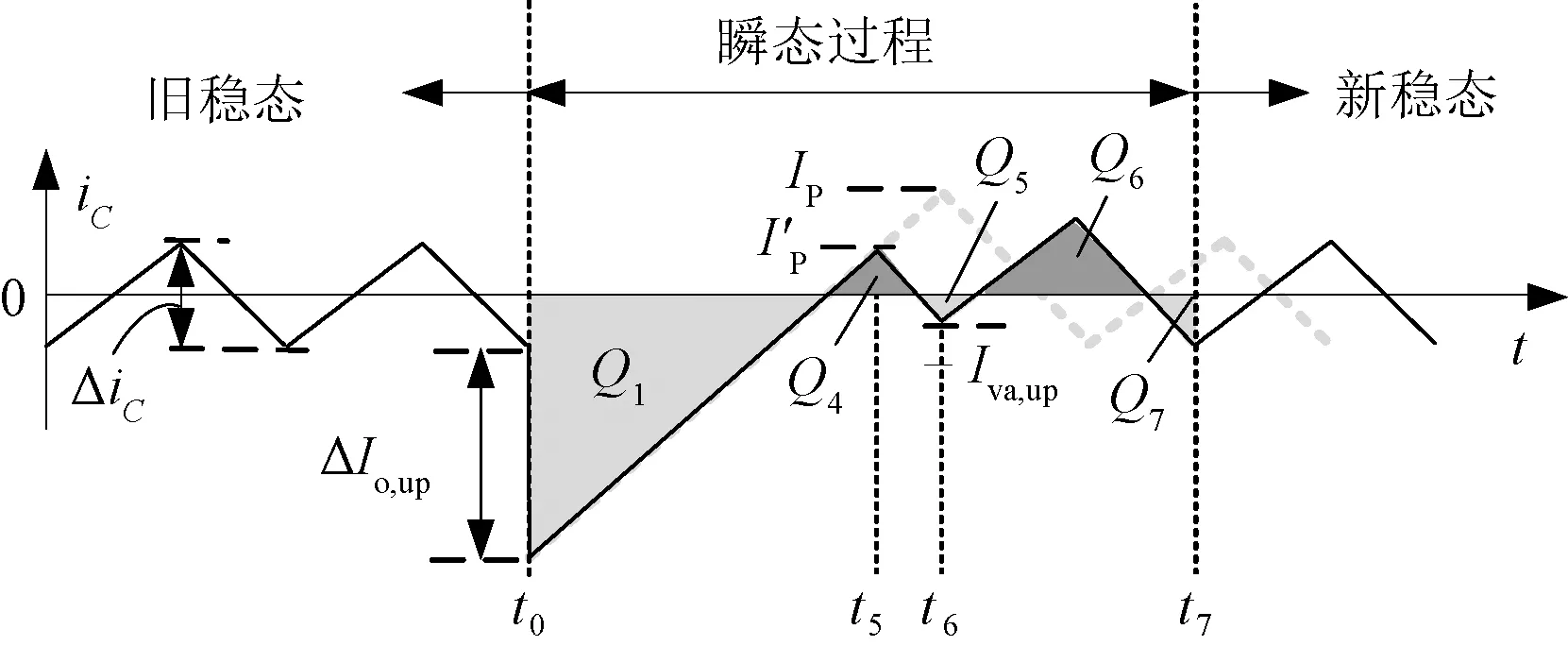
图4 最坏负载加载点的实际最优瞬态过程Fig.4 Actual optimal transient process at the worst load step-up point
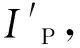
(3)
I′P=Nm1TON-0.5ΔiC-ΔIo,up
(4)
式中,floor(·)为向下取整函数。然后,iC开始下降,在t=t6时刻控制内环总反馈信号vsum下降到控制信号vcon,触发导通定时器开始计时,同时iC下降到谷值-Iva,up;随后,iC经历1个TON后开始下降,在t=t7时刻进入到新稳态。由于图4中的Q7与图3中的Q3相等,则有:
Q2=Q4+Q6-Q5
(5)
其中
在图4中,根据t0~t6时间间隔内输出电容充电电荷和放电电荷间的关系以及多环路COT控制的控制机制,可以计算出等效输出电容ESR为:
(6)
式中,req,up=ωc,upKc+ωv,upKvr,ωc,up、ωv,up分别为加载情况下的ωc,ωv。Iva,up可以由式(5)求得。
由式(2)~式(6)可以求出多环路COT控制Buck变换器在最坏加载点处加载具有最优加载瞬态性能时的电感电流权重。
3.2 优化负载减载瞬态性能的权重配置
当负载减载点发生在开关管导通期间,由于导通时间固定,开关管无法立即关断,导致控制电路无法及时对负载减载做出响应,从而影响瞬态响应速度。当负载减载点在固定导通时间开始时刻(即关断时间结束时刻),控制电路对负载减载做出响应的延迟时间最长,故该时刻为最坏负载减载点。根据多环路COT控制Buck变换器的工作原理可知,若负载在最坏减载点减载,实现最优瞬态性能的瞬态过程如图5所示。
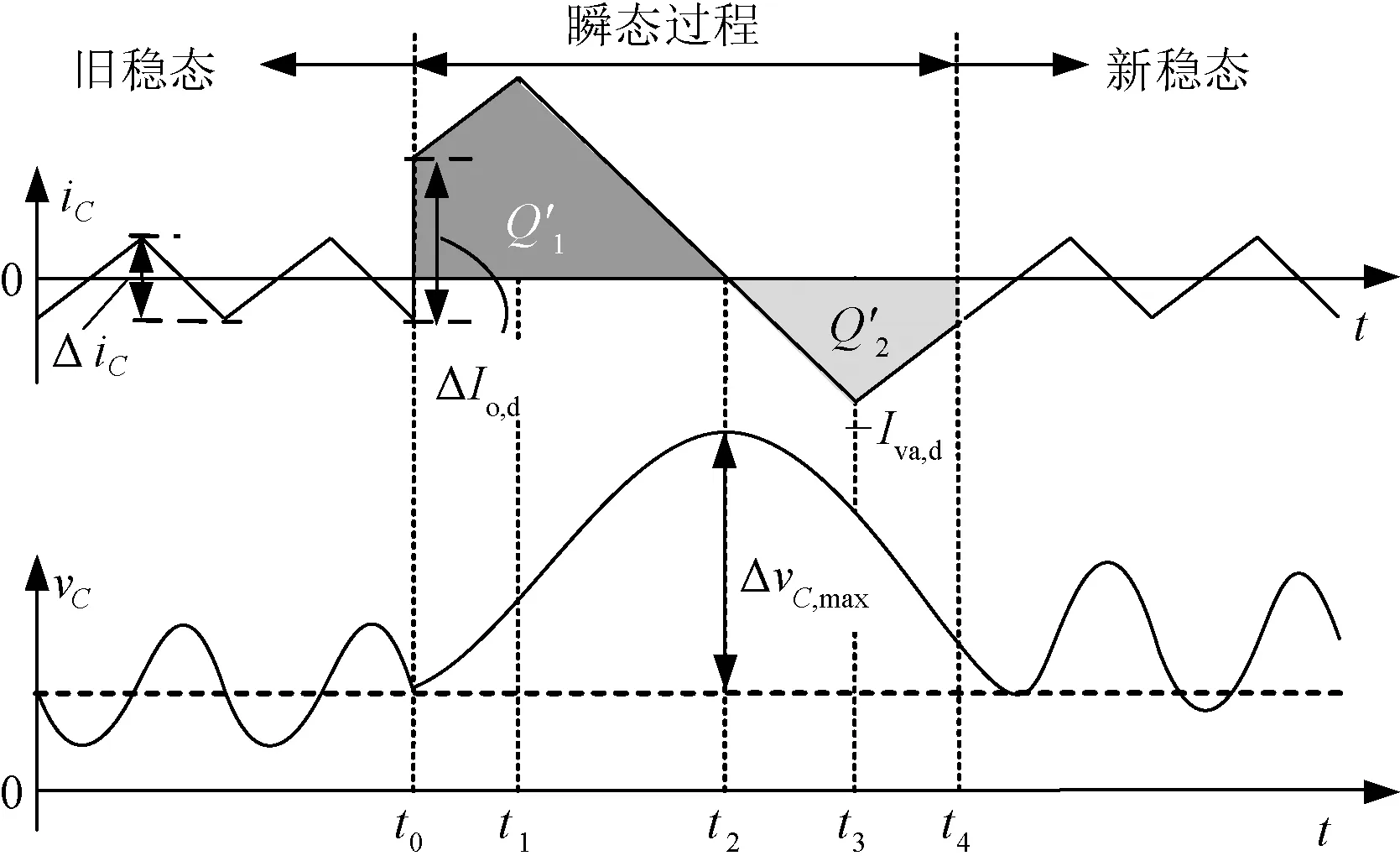
图5 最坏负载减载点的理想最优瞬态过程Fig.5 Optimal transient process at the worst load step-down point
在图5中,负载电流Io在t=t0时发生跳变,跳变量为ΔIo,d,该跳变量同样立即体现在电容电流上。在随后的瞬态过程中,iC和vC的变化为:在t=t0时,iC从iC=ΔIo,d-0.5ΔiC处开始上升,上升斜率为m1,同时输出电容充电,vC开始上升;在t=t1时,开关管S关断,iC开始下降,下降斜率为m2,vC继续上升;在t=t2时,iC=0 A,vC具有最大上冲量,随后vC开始下降。在t=t3时,vsum下降到vcon,使开关管S导通,iC开始上升;在t=t4时,iC=-0.5ΔiC刚好进入到新稳态。
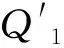
Qin=Q′1-Q′2
(7)
其中
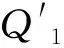
在图5中,根据t0~t4时间间隔内输出电容充电电荷和放电电荷间的关系以及多环路COT控制的控制机制,可以计算出等效输出电容ESR为:
(8)
式中,req,d=ωc,dKc+ωv,dKvr,ωc,d、ωv,d分别为减载情况下的ωc、ωv。
由式(7)和式(8)可以求出多环路COT控制Buck变换器在最坏减载点处减载具有最优减载瞬态性能时的电感电流权重。
3.3 优化瞬态性能的权重配置策略
首先,由文献[9]可知,当输出电容ESR较小,即2rC (9) 式中,κ=R/(R+r)。所以,在权重配置过程中,必须确保电感电流权重始终满足式(9)。 其次,在多环路COT控制Buck变换器实际工作过程中,负载的加载和减载往往是同时存在的,且两种情况下最优电感电流权重往往是不同的。此时,优化瞬态性能的依据为: 若负载加载时和减载时的最优电感电流权重均满足式(9),在加载影响较大的场合(如占空比较大的场合),选择负载加载时的最优电感电流权重ωc,up;在减载影响较大的场合(如占空比较小的场合),选择负载减载时的最优电感电流权重ωc,d。 若负载加载时的最优电感电流权重不满足式(9),则选择负载减载时的最优电感电流权重;反之亦然。 若负载加载和减载时的最优电感电流权重均不满足式(9),则选择满足式(9)且考虑一定稳定裕量的最小电感电流权重。 利用多环路COT控制Buck变换器的PSIM仿真电路和表1的电路参数分别验证负载加载和减载时实现最优瞬态性能的电感电流权重。 在最坏负载加载点加载时,选择g= 3.3,负载电流Io从5 A跳变到7 A,负载加载量ΔIo,up为2 A。结合式(6)和表1的电路参数,可计算出负载加载时的最优电感电流权重为ωc,up= 0.11,该权重满足式(9)。为了验证式(6)的正确性,分别选取ωc,up=0.07、0.112和0.16进行PSIM电路仿真,相应的仿真结果如图6(a)所示。从图中可以看出,当ωc,up=0.112时,多环路COT控制Buck变换器具有最优加载瞬态性能。当ωc,up= 0.16时,输出电压下冲量和恢复时间均增大;当ωc,up= 0.07时,输出电压出现欠阻尼振荡现象。 图6 ΔIo=2 A时,不同权重配置的输出电压仿真波形Fig.6 Simulation waveforms of output voltage under different weight configurations at ΔIo=2 A 在最坏负载加载点加载时,选择g= 2,负载电流Io从7 A跳变到5 A,负载减载量ΔIo,d为2 A。结合式(8)和表1的电路参数,可计算出负载减载时的最优电感电流权重为ωc,d= 0.053,该权重满足式(9)。为了验证式(8)的正确性,分别选取ωc,d=0.042、0.058和0.1进行PSIM电路仿真,相应的仿真结果如图6(b)所示。从图中可以看出,当ωc,d=0.058时,多环路COT控制Buck变换器具有最优减载瞬态性能。三种电感电流权重情况下,输出电压的上冲量基本相同,但当ωc,d=0.1时,恢复时间增大;当ωc,d=0.042时,输出电压出现欠阻尼振荡现象。 进一步,仿真分析了负载电流Io从4 A跳变到7 A再跳回4 A(ΔIo跳变量为3 A)的情况。在表1中,将电容值C和ESR的r值分别改为300 μF和1 mΩ,Vref改成4 V,其他参数不变。根据式(6),可计算出负载加载时的最优电感电流权重为ωc,up= 0.043,该权重满足式(9);根据式(8),计算出负载减载时的最优电感电流权重为ωc,up=0.027,该权重也满足式(9)。为了验证式(6)的正确性,分别选取ωc,up=0.018、0.035和0.055进行PSIM电路仿真,相应的仿真结果如图7(a)所示。从图7(a)可以看出,当ωc,up=0.035时,多环路COT控制Buck变换器具有最优加载瞬态性能。当ωc,up=0.055时,输出电压下冲量和恢复时间均增大;当ωc,up=0.018时,输出电压出现欠阻尼振荡。 图7 ΔIo=3 A时,不同权重配置的输出电压仿真波形Fig.7 Simulation waveforms of output voltage under different weight configurations at ΔIo=3 A 为了验证式(8)的正确性,分别选取ωc,d=0.018、0.027和0.04进行PSIM电路仿真,相应的仿真结果如图7(b)所示。从图中可知,当ωc,d=0.027时,多环路COT控制Buck变换器具有最优加载瞬态性能。三种电感电流权重情况下,输出电压的上冲量基本相同,但当ωc,d=0.04时,恢复时间增大;当ωc,d=0.018时,输出电压出现欠阻尼振荡现象。 对比仿真结果和理论分析结果,虽存在一定的误差,但在可接受范围内。因此,仿真结果验证了理论分析的正确性。 搭建多环路COT控制Buck变换器的实验样机,如图8所示。其中,开关管S采用型号为IRF540的MOSFET,二极管VD采用型号为MBR2045CT的肖特基二极管,电感电流采样电路是采用型号为LM7171的运算放大器搭建的差分放大电路,比较器型号为LM319,PI补偿器由型号为LT1357的运算放大器搭建,导通定时器由型号为LM334可调恒流源芯片为电容充放电来实现,驱动芯片型号为IR2125。 图8 实验样机Fig.8 Experimental prototype 利用图8的实验样机,选择图6中的电路参数和权重配置进行硬件电路实验,相应的输出电压实验波形分别如图9(a)和图9(b)所示。在图9(a)中,负载电流从5 A跳变到7 A,当ωc,up=0.112时,多环路COT控制Buck变换器的负载加载瞬态性能最优;当ωc,up=0.16时,输出电压下冲量明显增加;当ωc,up=0.07时,输出电压出现欠阻尼振荡现象,导致输出电压出现上冲。在图9(b)中,负载电流从7 A跳变到5 A,当ωc,d=0.058时,多环路COT控制Buck变换器的负载减载瞬态性能最优;当ωc,d=0.1,输出电压的恢复时间明显增加;当ωc,d=0.042时,输出电压出现欠阻尼振荡现象,导致输出电压出现下冲。 图9 ΔIo=2 A时,不同权重配置的输出电压实验波形Fig.9 Experimental waveforms of output voltage under different weight configurations at ΔIo=2 A 对比图9和图6,实验结果与仿真结果基本一致,从而验证了仿真结果的正确性。需要说明的是,在实验过程中,电感电流和输出电压的权重配置是通过高精度电位器的调节实现的。 多环路COT控制Buck变换器的瞬态性能与电感电流权重和输出电压权重的配置密切相关。本文基于电容电荷平衡原理,通过时域分析给出了负载加载时和减载时实现最优瞬态性能的权重配置,进而提出了优化负载瞬态性能的权重配置策略。电路仿真结果和实验结果验证了理论分析的正确性。结果表明,负载加载或减载时采用最优权重配置时,多环路COT控制Buck变换器不存在欠阻尼振荡且输出电压的过冲量最小、恢复时间最短。当电感电流权重大于其最优权重,负载加载时输出电压下冲量和恢复时间均增大,负载减载时输出电压上冲量不变但恢复时间增大;反之,负载加载和减载时输出电压均出现欠阻尼振荡现象。研究结果可为多环路COT控制开关变换器的瞬态性能优化提供理论指导。4 电路仿真与硬件实验验证
4.1 电路仿真验证
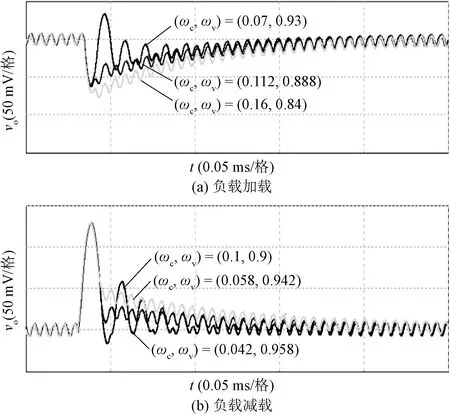
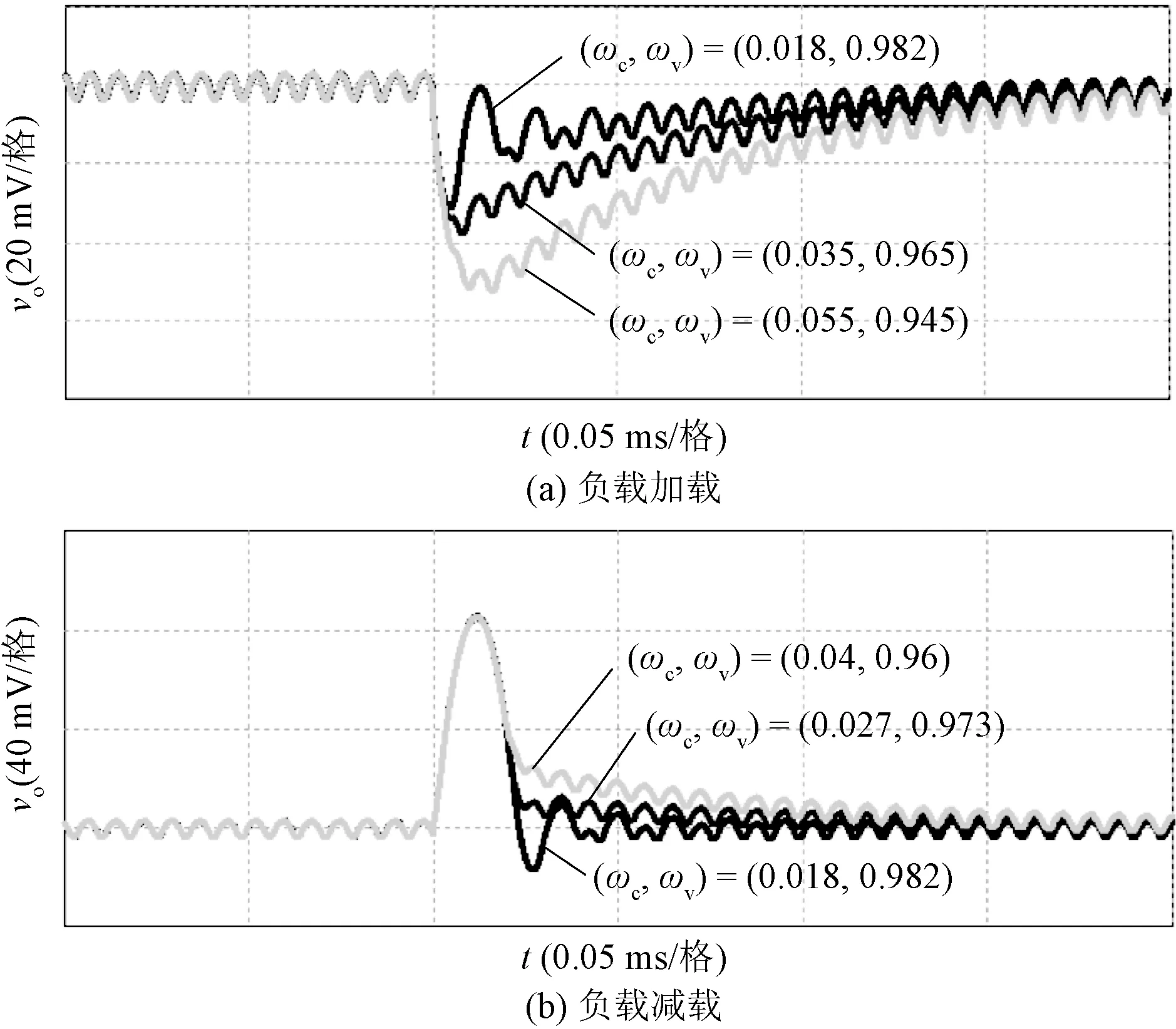
4.2 硬件实验验证

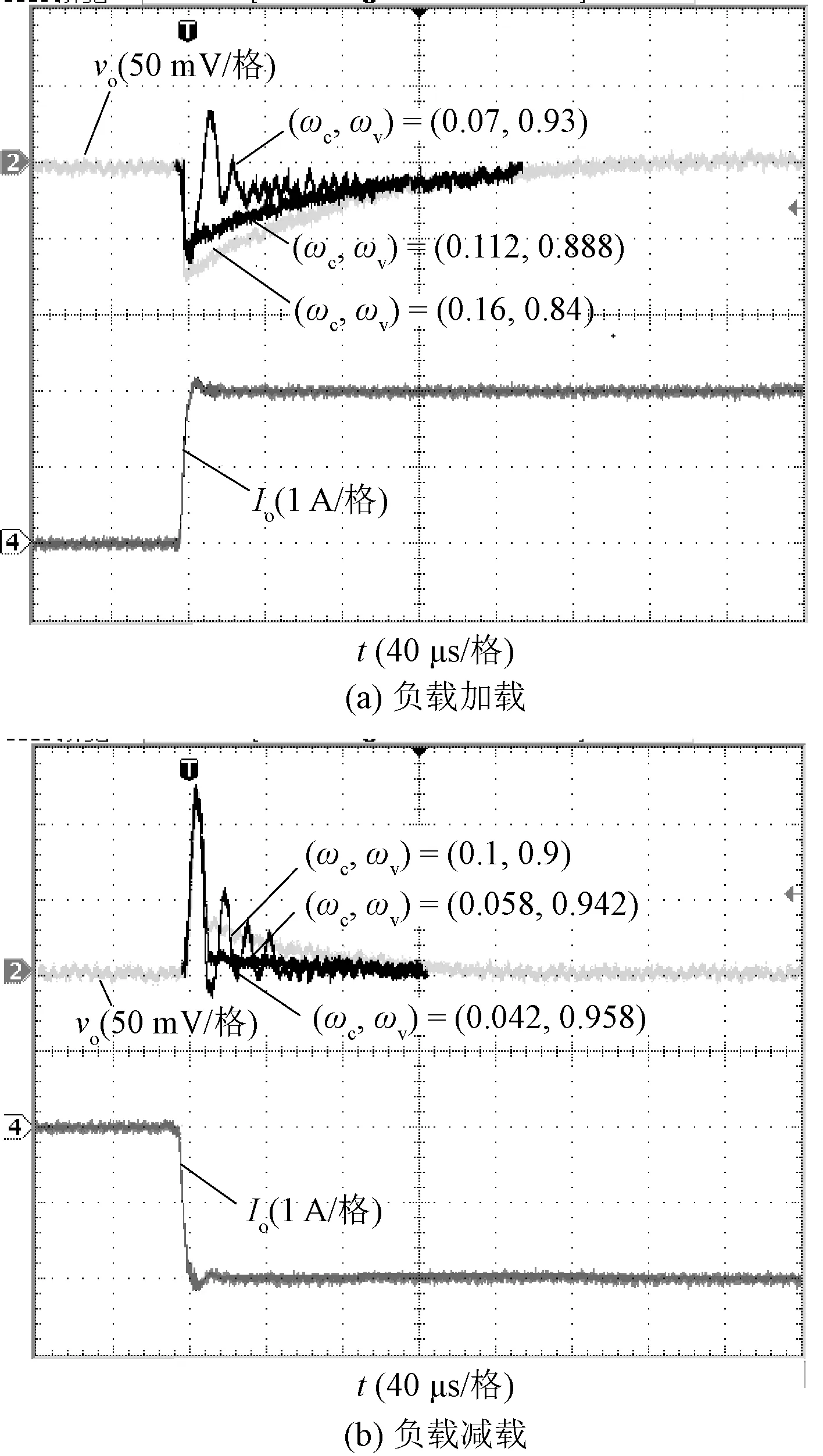
5 结论
