功率互济的多独立微电网运行优化及分析
2022-04-01邢毓华侯静茹
邢毓华, 侯静茹, 支 娜
(西安理工大学自动化与信息工程学院, 陕西 西安 710048)
1 引言
我国海岸线长,人口密度大,存在很多因地理位置而无法依靠大电网供电的地区。为保障海岛沿岸居民的正常生活和发展,常采用海缆供电和柴油机进行发电,但是存在故障频发,污染大等问题。随着分布式可再生能源(Renewable Distributed Generator, RDG)和微电网(MicroGrid,MG)技术的发展[1,2],利用可再生的清洁能源——光能、风能等分布式电源,为独立的MG提供能量,可因地制宜地利用当地可再生能源。但单一独立的微电网存在电力不稳定、容量有限、鲁棒性差、运行成本高等缺点,同时因为海岛地区的天气多变,分布式电源具有间歇性和随机性,使得微电网不能可靠稳定地运行[3,4]。为解决单个微电网的不可靠问题,研究者提出了“More Microgrids”计划,将地理位置上毗邻的微电网互联,构成多微电网群系统。
随着多微电网系统成为时代热点,将多个离网的微电网进行互联,构成多独立微电网(Multi-Independent-MicroGrid, MIMG)。研究MIMG系统的能量调度管理成为当今重点。虽然MIMG系统互联可以加强供电稳定性、加强对可再生能源的利用、减少对能量的消耗、提高MIMG群的鲁棒性和降低运行成本,但是对于多微电网独立运行和互联运行之间切换的界限没有明确的界定,微电网之间进行功率互济的条件,以及保证微电网独立运行和互联运行的可靠运行策略还有待研究。国内外对MIMG的运行研究已经有了一些成果[5-10]。文献[5]只研究了单个微电网的运行优化问题;文献[6]考虑了相邻MG在不同的决策下的能量管理,但是没有考虑储能系统;文献[7]没有对储能系统进行约束;文献[8]只考虑了微电网与大电网之间的交互,而没有研究独立微网之间的互济;文献[9]考虑了多微网群在独立运行的情况下微电网紧急调度能量的策略,但未综合考虑各个组件的优化运行;文献[10]考虑了双微网系统的在线运行优化策略,但是忽略了微网间切换阈值的范围;文献[11]虽然考虑了微网之间的自适应切换阈值,但是未考虑多个微电网独立运行的情况;文献[12]采用双层优化模型,提出一种基于源网荷互动的互联微电网能量管理模型,但是没有考虑到微网独立运行互联的情况;文献[13]仅考虑到可再生能源对多微电网的能量管理系统的鲁棒性。对多微电网能量优化调度运行方面的研究,已存在一些研究成果。文献[14]考虑了合作博弈的多微电网系统的决策模型,实现了合作期间的储能资源的优化利用,但是对于微电网其他组件考虑不是很充分;文献[15]提出了离网临近海岛微电网运行方案,采用结合蒙特卡模拟的粒子群算法(Monte Carlo Simulation combined Particle Swarm Optimization,MCS-PSO)对模型求解;文献[16]提出多微电网分别在结构和能源调度策略的方法;文献[17]引入多代理系统的多微网群协调控制策略,但是未考虑微网间互济的阈值;文献[18]在多种微电网的微网模型上,提出了一种通过改进粒子群优化算法对微网系统进行经济优化运行的方法;文献[19]以综合运行成本和环境成本为优化目标,融合了快速非支配排序遗传算法和自适应布谷鸟算法。上述研究多是考虑微电网独立运行和多微电网并网运行的运行策略,很少有考虑到微电网之间切换的阈值。如果忽略微电网之间切换阈值,微电网会因为进行频繁切换造成不必要的能量损耗和器件老化,最后可能会导致微电网之间无法进行互济,造成微网群不能可靠稳定运行、经济成本高等重大问题,同时粒子群算法适合解决微电网之间的组合问题,但不适合大规模计算,计算时间过长,需要对其进行处理改进。
因此,本文针对MIMG系统中多独立微电网互联和独立运行之间的切换阈值问题进行研究,同时以系统中的燃气轮机购电成本、燃机启停成本、电池损耗成本和线路传输成本最低为目标。同时MIMG系统采用聚类分析和粒子群优化算法相结合的手段确定阈值。本文首先建立独立微电网结构和双微网互联运行的结构和数学模型;然后建立双微电网可靠运行的两种能量管理策略;接着使用聚类分析结合粒子群优化算法确定切换的阈值;最后通过仿真验证等级划分管理策略的运行成本优于双微网能量管理策略。
2 双微电网的系统结构及集群建模
双微电网的系统集群在进行互联时,微电网的净功率和储能电池的充放电在微电网互济过程中决定微网能够互济给相邻微网的交换功率(SWitching power, SW)大小,对选择微网运行策略的关键问题有决定作用。
2.1 双微网系统结构
本系统是基于能量路由器(Energy Router, ER)的双微网系统[10],如图1所示。由两个独立的微电网通过能量路由器进行能量互济,每个微电网由光伏发电(PhotoVoltaic, PV)、风力发电(Wind Turbine, WT)、储能电池组(Energy Storage System, ESS)和微型燃气轮机(Micro-Turbine, MT)共同为用户侧的负荷(Load)进行供电。
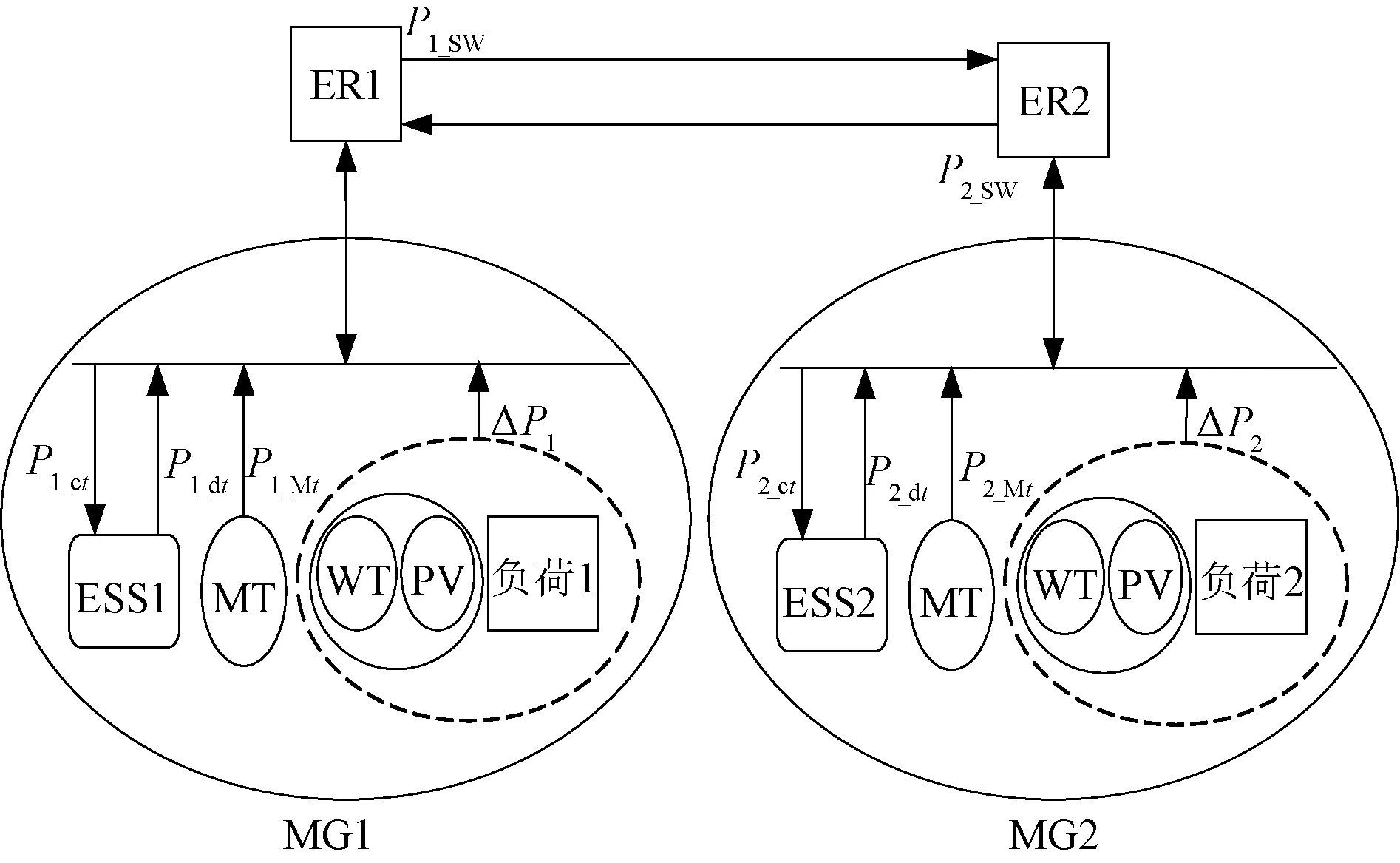
图1 双独立微网互联系统Fig.1 Two independent microgrid interconnection systems
运行周期为T时段,其中时段t∈T={1,2,…,24},图1中,Pi_SW为t时段微网i输出微网间的互济功率,i=1,2;Pi_Mt为微网i中燃气轮机输出的功率;Pi_ct、Pi_dt分别为微网i储能系统的充、放电功率;ΔPi为微网i的净功率。
为了便于分析和观察,本文采用准静态时变负荷模型,规定负荷在某些时间段是恒定的,但是在不同的时间段内是可以进行变化的。
2.2 双微电网集群优化建模
2.2.1 目标函数
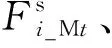
(1)
(2)
(3)
Fi_batt=βbatt(Pi_ct+Pi_dt)
(4)
Fi_loss=Pi_SWCloss
(5)
式中,Ci_Mt为微型燃气轮机的燃料成本;cU、cD分别为机组的单元启、停机成本,元/次;ui,t、εi,t分别为描述微电网i中的微型燃气轮机在时段t内开、关机状态的二进制变量;βbatt为充放电功率大小的寿命损耗系数;Closs为线路损耗的成本。
2.2.2 储能系统
t时段的微网i内,ESS的充电、放电功率Pi_ct≥0、Pi_dt≥0,充电、放电效率范围为ηi_ct(0≤ηi_ct≤1)、ηi_dt(0≤ηi_dt≤1),储能系统的荷电状态(State of Charge,SOC)代表储能电池的剩余容量,充电过程的关系为:
(6)
放电过程的关系为:
(7)
式中,SOC(t+1)和SOC(t)分别为t+1时刻和t时刻的储能电池的剩余电能;Ei_ap为储能电池的容量。
为防止电池过充过放,需对荷电状态进行约束,SOCmax和SOCmin分别代表两个微网的储能电池荷电状态的最大值和最小值,则储能电池充放电功率约束和荷电状态约束为:
Pi_batt_min≤Pi_ct≤Pi_batt_max
(8)
Pi_batt_min≤Pi_dt≤Pi_batt_max
(9)
SOCmin≤SOC≤SOCmax
(10)
式中,Pi_batt_max和Pi_batt_min分别为储能电池的充放电的上、下限;同时Pi_batt_max为储能电池的功率容量。
2.2.3 净功率
在研究多微电网互联的系统中,净功率对于判断微电网是否互联有着至关重要的作用。t时段净功率是微网i中的可再生能源与负荷的差,ΔPi>0证明微电网处于超额状态,可再生能源不仅可以满足负荷的需求,还有盈余;ΔPi<0证明微电网处于缺额状态,可再生能源不能满足负荷。关系式为:
ΔPi=Pi_PV+Pi_WT-Pi_Load
(11)
式中,Pi_PV为微网i中光伏电池组的发电功率;Pi_WT为微网i中风力发电机组的发电功率;Pi_Load为微网i的负荷总功率。
2.2.4 微网互济功率
在微网互联的过程中,t时段微电网与相邻微电网进行能量互济,需要经过两个微网之间的输电线才能进行能量传递。通常通过输电线传递时,需要关注输电线路的电阻造成的能量损耗,由交换功率Pi_SW引起的传输损耗为:
(12)
(13)
式中,r为微网之间输电线的单位长度电阻,Ω/km;l为微电网之间的距离,km;V为微电网的运行电压等级。当Pi_SW-Ploss>0时,微电网才能够进行功率互济。
2.2.5 功率平衡约束
每个微电网需满足系统的出力、从微型燃气轮机获得的能量、从相邻微电网获得的交换功率及输电线的损耗的和达到动态平衡,关系式如下:
ΔPi+Pi_Mt+Pi_ct-Pi_dt-Ploss≥0
(14)
式中,如果等号成立,证明两个微电网是处于功率平衡状态;当ΔPi≥0,证明微电网的可再生能源足够供应负荷,微网处于超额状态,此时燃气轮机不工作,功率为0,多余的能量弃光弃风。
3 双微网互联系统能量管理策略
双微电网之间进行功率互济,必须着重讨论储能电池、净功率与购电量之间的平衡。由于可再生能源和负荷具有波动性和随机性,所以必须有针对于实时变化情况下的策略。本文提出了先充电后互济和先互济后充电两种策略,以三组独立微电网为研究对象,两两构成双微网集群共三组组成研究组,互为对照组。
3.1 先充电后互济策略
当微电网处于超额状态时,先给该微电网的储能电池充电,若还有盈余则互联给相邻微网进行互济或者给其储能系统充电。
(1) ΔP1≥0,ΔP2≥0,双微电网都处于超额状态,此时先将多余的功率为储能电池进行充电。
(15)
(16)
1)SOC1(t+1)=SOCmax,SOC2(t+1)=SOCmax,两个微电网不仅都处于超额状态且各自的内部储能电池都已充满,微电网之间不互联,多余的功率弃光弃风。
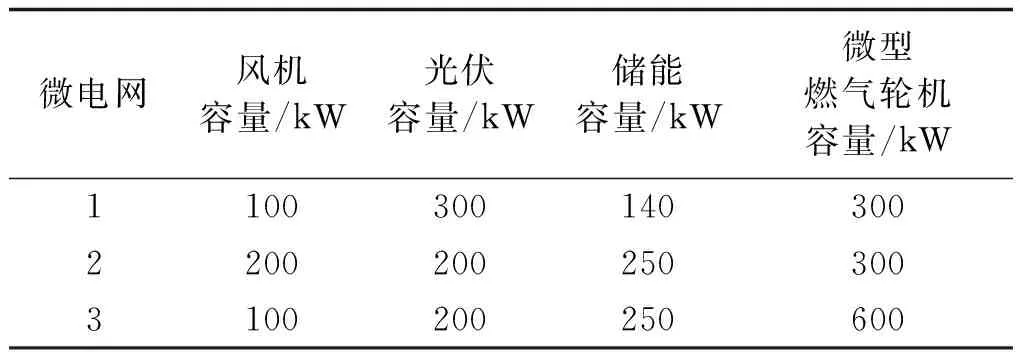
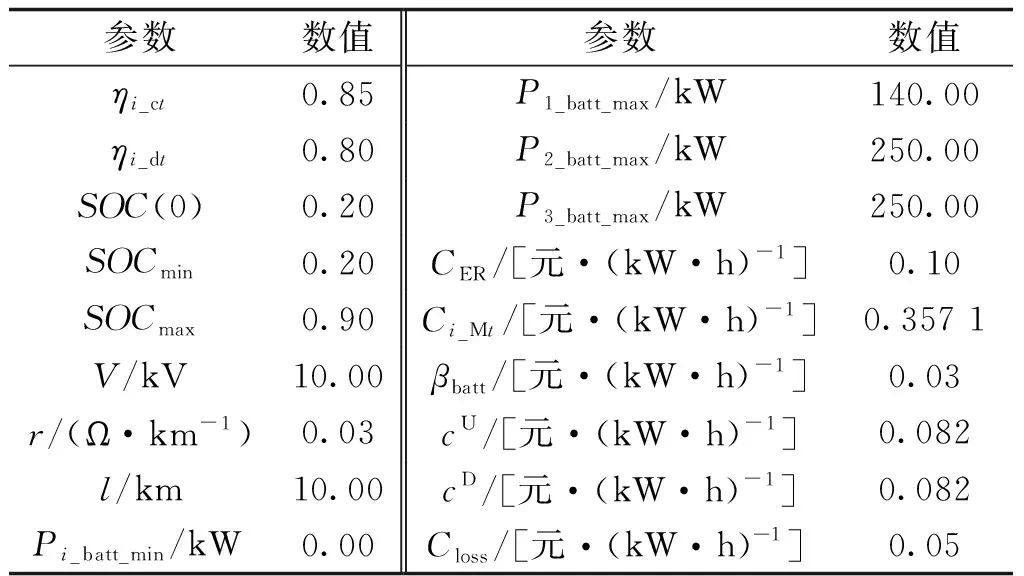
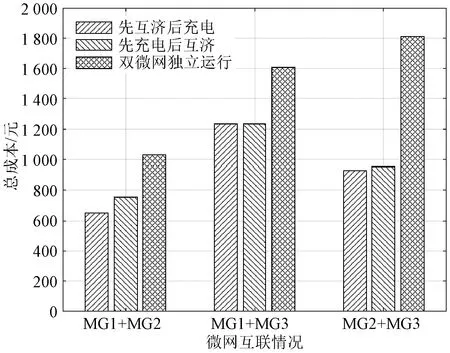
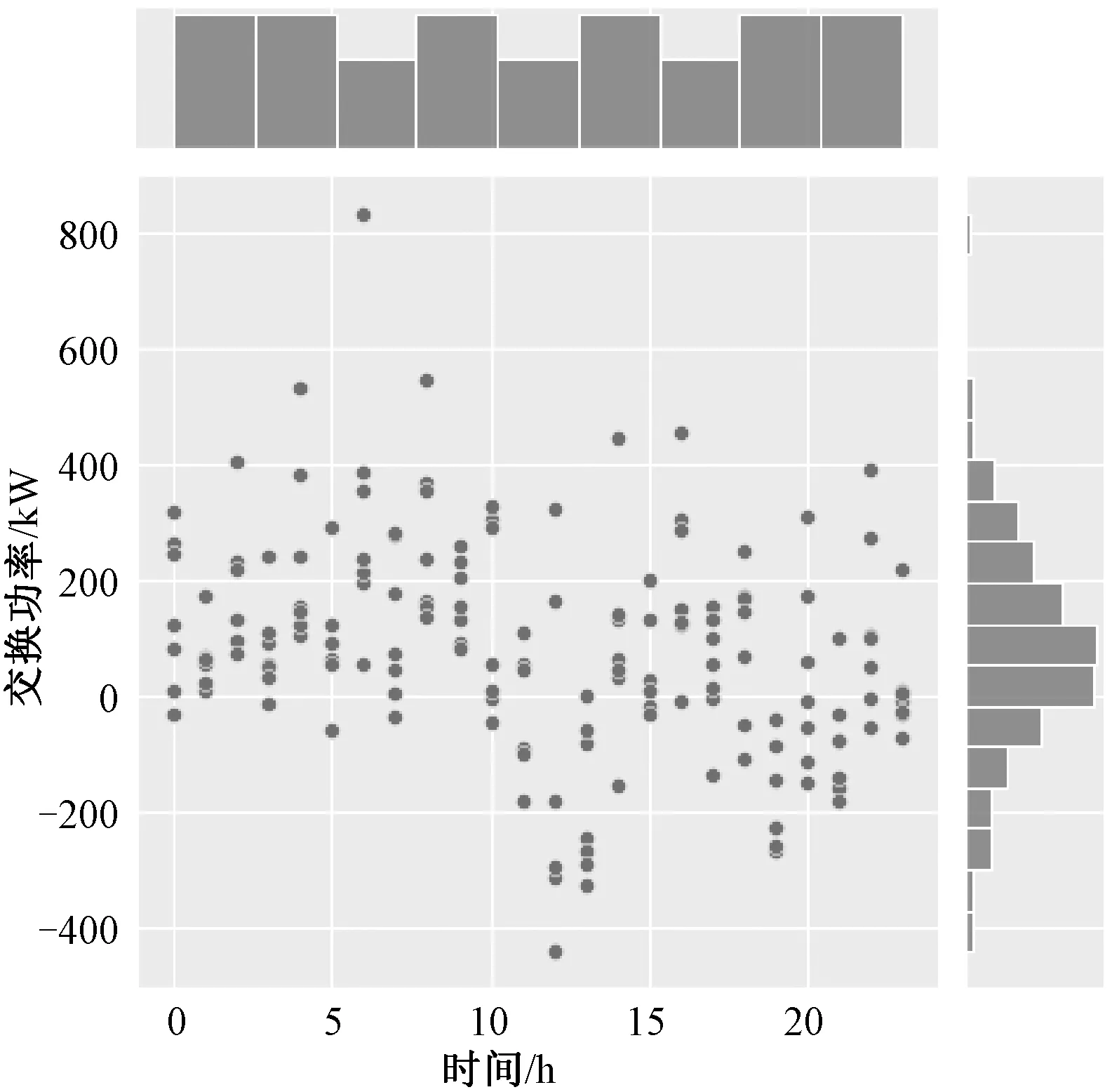
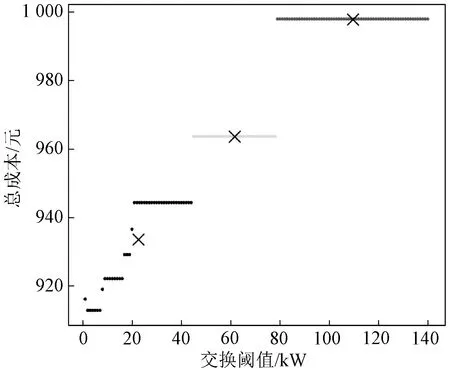
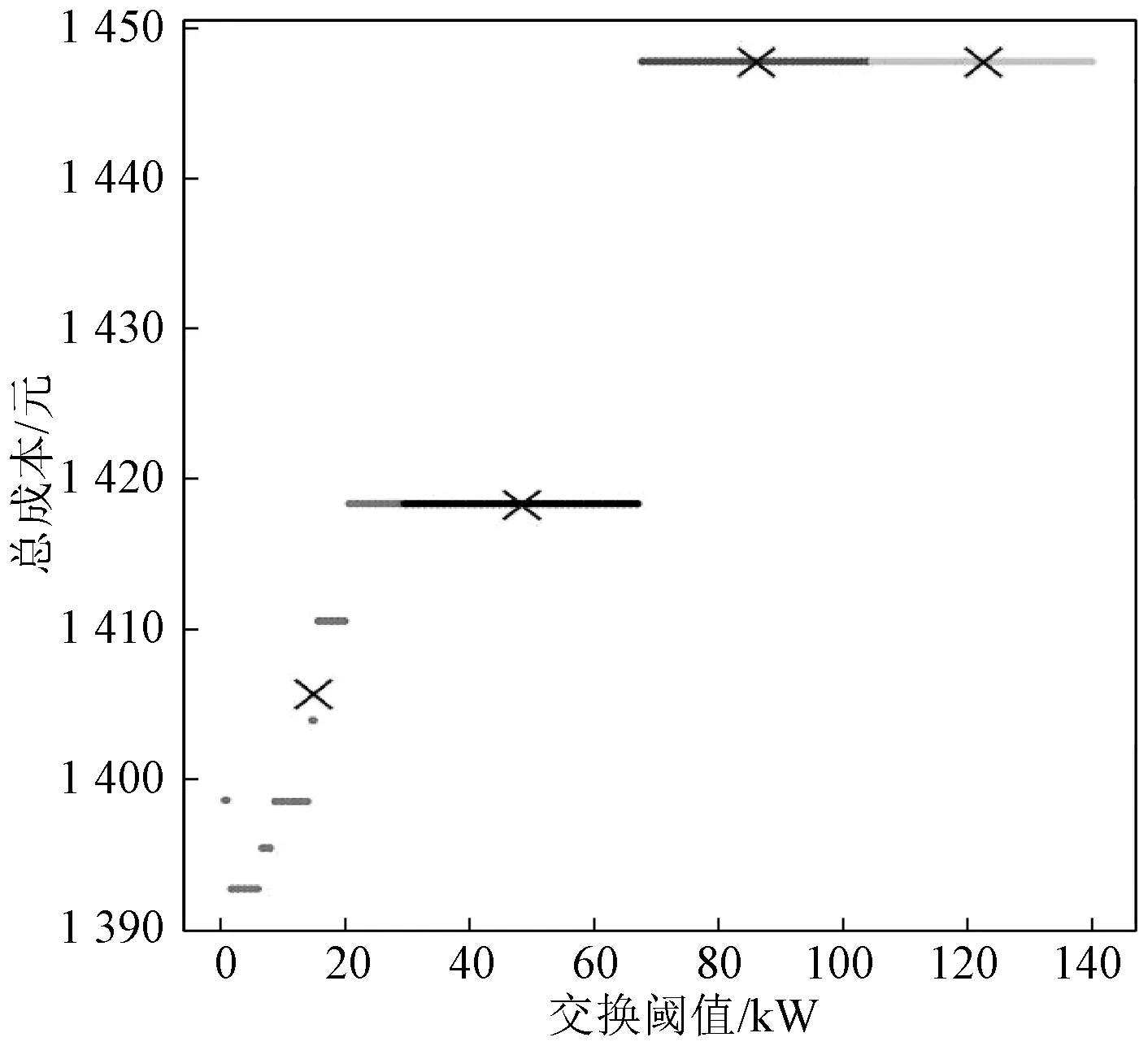
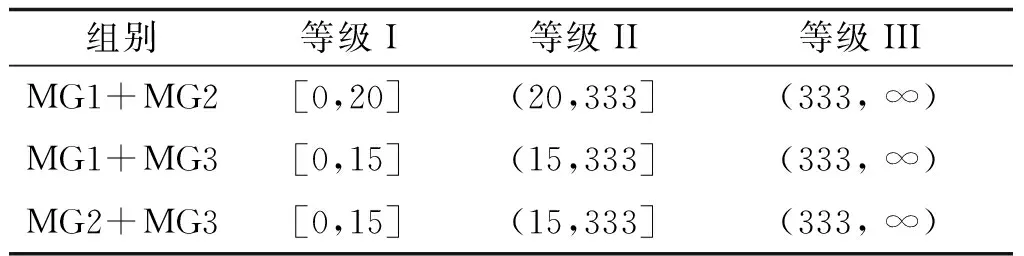
2)SOC1(t+1) 3)SOC1(t+1)=SOCmax,SOC2(t+1) P1_SW=ΔP1-P1_ct (17) (18) (19) 4)SOC1(t+1) (2) ΔP1<0,ΔP2<0,双微电网都处于缺额状态,所以双微电网不会进行互联。此时各微网的储能电池先放电补偿微网缺少的功率,如果储能电池的放电量还不能满足缺额功率,则微型燃气轮机进行发电补偿缺额量。 (20) (21) Pi_Mt=-ΔPi-Pi_dt (22) (23) (24) P1_SW=ΔP1-P1_ct (25) (26) (27) (28) (29) (30) P2_Mt=-ΔP2-P2_dt (31) (4) ΔP1<0,ΔP2≥0,双微网此时的运行状态与(3)相同。 如果微电网处于超额状态,微网间先互济能量,有剩余功率则为自身储能系统充电。 (1)ΔP1≥0,ΔP2≥0,双微电网都处于超额状态,这种情况和3.1节中的第(1)种情况一样。 (2)ΔP1<0,ΔP2<0,双微电网都处于缺额状态,不互联,这种情况和3.1节中第(2)种情况一样。 (3)ΔP1≥0,ΔP2<0,此时MG1处于超额状态,MG2处于缺额状态,MG1的超额功率先补偿MG2的缺额功率,此时MG1传输的功率是其超额的功率。 P1_SW=ΔP1 (32) (33) P1_ct=ΔP1+ΔP2 (34) (35) (36) (37) (38) (39) (40) (41) P2_Mt=-ΔP2-P2_dt (42) (4)ΔP1<0,ΔP2≥0,此时MG2处于超额状态,MG1处于缺额状态,MG2先补偿MG1的缺额量,这种情况和第(3)种情况一样,不过是MG1和MG2的位置发生了互换,所以下标需要更换。 本系统主要是分析微网互济功率对总运行成本的效果和影响,讨论了上述先充电后互济策略和先互济后充电策略对购电量的需求。 3.3.1 研究对象及相关基础数据 在独立微电网中风、光、储和燃气轮机的容量是决定总运行成本的关键因素之一,对独立微电网各组件容量进行粒子群优化算法,迭代次数400次,选取3个交换功率差别最大且成本最优组件容量的独立微电网,独立微电网系统参数设置见表1。 表1 独立微电网系统参数设置Tab.1 Parameter setting of independent microgrid system 本节研究双微网系统的两个能量管理运行策略的有效性。先设相邻微电网距离相同为10 km。线路参数和储能系统参数见表2。 表2 系统参数Tab.2 System parameters 3.3.2 不同策略下微网购电成本的比较与分析 MG1、MG2和MG3在相同的系统设置下,先充电后互济和先互济后充电两种策略与双微网无策略运行进行对比,经济成本都优于独立运行成本,如图2所示。 图2 不同集群在不同策略购电成本的比较Fig.2 Comparison of power purchase cost of different clusters under different strategies 从图2中MG1+MG2可以看出,先互济后充电策略购电成本比先充电后互济购电成本更优,原因是相邻的微电网将超额的功率传递给缺额的微网,电网可以减少购买成本,降低启停次数,因此先互济的运行策略优于先充电的成本。在MG1+MG3与MG2+MG3的双微网系统中两种策略几乎相等,是因为MG3的分布式电源容量配置较低,但是微型燃气轮机的容量是MG1和MG2的2倍,且燃气轮机的购电成本和启停成本对目标函数影响较大。其中MG2+MG3的看起来效果最好,是因为两个微电网的储能电池容量较大,储能电池可以将超额的容量进行大幅度的消纳,同时也可以在很大程度上为负荷提供能量,减少购电成本。 粒子群优化算法具有收敛速度快,原理简单易操作等优点,但是也存在容易陷入局部最优导致收敛精度低和不易收敛等缺点。先将阈值进行聚类分析,选出阈值范围,可以避免陷入局部优化、易发散等问题;再将小范围的阈值进行粒子群优化,可以提高运行速度,加快收敛速度。 独立微电网由于天气的间歇性和多变性导致微电网的交换功率也变得不确定。如图3所示为MG1、MG2和MG3三个微电网之间的交换功率生成的数据集,利用Python语言,在软件Jupyter Lab软件上对数据进行处理。 图3 交换功率分布的柱状图Fig.3 Histogram of switching power distribution 由图3可知,在时间上交换功率的大小除了用电高峰5∶00~7∶30、10∶00~12∶00和16∶00~18∶30几乎都是均匀的,且交换功率在0~50 kW之间的概率占27%。 考虑到长期的经济规划,选取先互济后充电的运行策略,同时为了避免微电网之间频繁进行功率交换,造成器件的加速损坏,对微电网传输到相邻微电网的净出力设定阈值,进行等级划分,分情况讨论使用不同的运行策略。 Pi_SW≥Pi_SW_range (43) 式中,Pi_SW_range为微电网能够进行交换的阈值。如果微网交换的净出力满足式(43),微电网才进行功率互济。判断三个双微网组合的阈值范围,选择从0 kW到140 kW和250 kW的阈值进行K-Means聚类,选取合适的簇,如图4~图6分别为三个集群的阈值聚类图,其中“×”代表聚类中心,“·”和“—”代表不同阈值的样本点和样本点叠加后的范围。图4~图6中发现明显的多个断层,并且随着阈值的增加,成本也显著增加。 图4 MG1和MG2阈值聚类图Fig.4 Threshold clustering diagram of MG1 and MG2 图5 MG1和MG3阈值聚类图Fig.5 Threshold clustering diagram of MG1 and MG3 图6 MG2和MG3阈值聚类图Fig.6 Threshold clustering diagram of MG2 and MG3 设计交换阈值,划分等级I(Pi_SW 针对聚类分析的阈值范围和等级的划分,采用粒子群算法对提出的模型进行求解。 在粒子群算法中设第i个粒子的N维位置矢量为Xid,由适应度函数得到粒子的适应度值;Vid为粒子i的速度[20]。每迭代一次,粒子通过个体极值和群体极值更新自身速度和位置,其更新公式如下: (44) (45) 通过粒子群优化算法的寻优极值,最终搜索得到最优交换功率切换阈值和最低运行成本。基于粒子群优化算法的优化模型求解流程图如图7所示。 图7 粒子群优化算法流程Fig.7 Flow chart of particle swarm optimization algorithm 将聚类分析结合粒子群优化算法确定交换功率的阈值。在Matlab中对阈值范围进行优化,迭代次数为1 000次,粒子规模为400个。选定K-Means聚类分析中的第一个簇,步长为5,选取聚类分析的第一个簇的范围进行粒子群优化,找出最佳的阈值。在讨论双微网阈值时设定相邻微网距离都为10 km,不同集群的等级划分见表3。 表3 不同组别的等级划分Tab.3 Classification of different groups 阈值等级划分策略是将所有的微网进行分组,每组由2个微网集群组成。首先需要判断独立微电网集群的运行状态,确认是否需要根据相邻的微网互联进行功率互济或者消纳,这个过程需要根据相邻微网的交换功率阈值进行判定;然后根据交换功率的大小划分等级,进行相应的能量管理策略,与之前的两种策略进行对比,图8列出了三组不同双微网集群的运行策略,进行总运行成本对比。由图8可以看出,MG1+MG2集群的总成本最小,且微电网互联的策略成本都比独立运行的成本少得多,表明针对不同集群在每种策略下其成本都可以达到一定程度的降低,其中本文采取的双微网系统等级划分策略的节省成本效果最好,比先互济后充电成本平均低4.6%,还有效地减少了微网之间的频繁切换,增强了稳定性。 图8 各种策略效果比较与分析Fig.8 Comparison and analysis of various strategies 本节将双微电网系统扩展到微电网集群互联系统。为了方便讨论,再加一组储能电池额定容量为140 kW、光伏额定容量为100 kW、风机额定容量为200 kW、微型燃气轮机额定容量为600 kW的微电网(MG4),切换阈值为20 kW,构成如图9所示的多微网系统集群。微电网之间通过能量路由器进行互济,相邻两个微电网的距离用lij表示,相邻微电网之间距离设置为l12=30 km,l13=15 km,l14=50 km,l23=60 km,l24=20 km,l34=40 km。 图9 多微网系统的集群方式Fig.9 Cluster mode of multi microgrid system 等级划分策略是将所有微电网集群进行分组,两两配对,所以适合偶数个数的微电网组成的系统。影响微电网集群方式的主要原因是相邻微电网之间的距离和微电网之间的交换功率。本文首先考虑所有集群互联的情形;然后采取等级划分的优化策略遍历所有集群,等级划分的优化策略是综合考虑相邻微电网之间的距离和微电网之间的交换功率切换阈值;最后再与先充电后互济的运行策略进行比较,证明等级划分的有效性。 不同集群下各种策略的节省成本比例见表4,可以看出情形2中总成本最小。两种策略降低的成本对比见表5。 表4 不同集群下各种策略的节省成本比例Tab.4 Cost saving ratio of different strategies in different clusters 表5 两种策略降低的成本对比Tab.5 Cost reduction comparison of two strategies 结果显示,在先互济后充电策略的基础上进行的等级划分策略节省成本的力度相比于先互济后充电的更大。 本文研究了多微网的运行优化问题。介绍了独立微电网和双微网互济的系统结构,建立了独立微电网集群优化模型。基于独立双微电网功率互济的模型提出了两种优化策略,并将功率互济的不同策略下微网购电成本进行比较分析,证明先互济后充电策略优于先充电后互济策略。考虑到微网之间的稳定性和可靠性,减少微电网之间频繁进行功率互济,将先充电后互济策略进行优化,利用聚类分析和粒子群优化算法对相邻微电网之间交换功率采用等级划分策略。仿真结果表明,本文采用的双微电网系统等级划分策略比先充电后互济策略成本平均低3.26%,减少微网之间的频繁切换,对提高微电网的可靠性具有重要意义。 本文提出的微电网系统等级划分策略仅考虑了偶数个数的独立双微电网组成的集群功率互济,未来将进一步对微电网的不同集群的所有情况进行研究。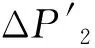
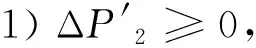

3.2 先互济后充电策略
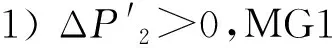
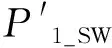

3.3 双微网策略的求解和分析
4 聚类分析结合粒子群优化算法等级划分
4.1 聚类分析初定阈值范围

4.2 粒子群优化算法优化互联阈值
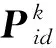

4.3 阈值与等级划分策略验证和分析
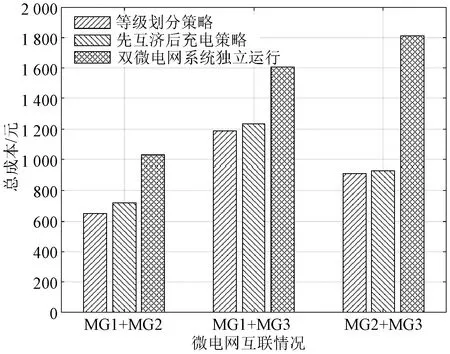
5 多微电网互联的算例验证与分析
5.1 多微电网系统集群方式
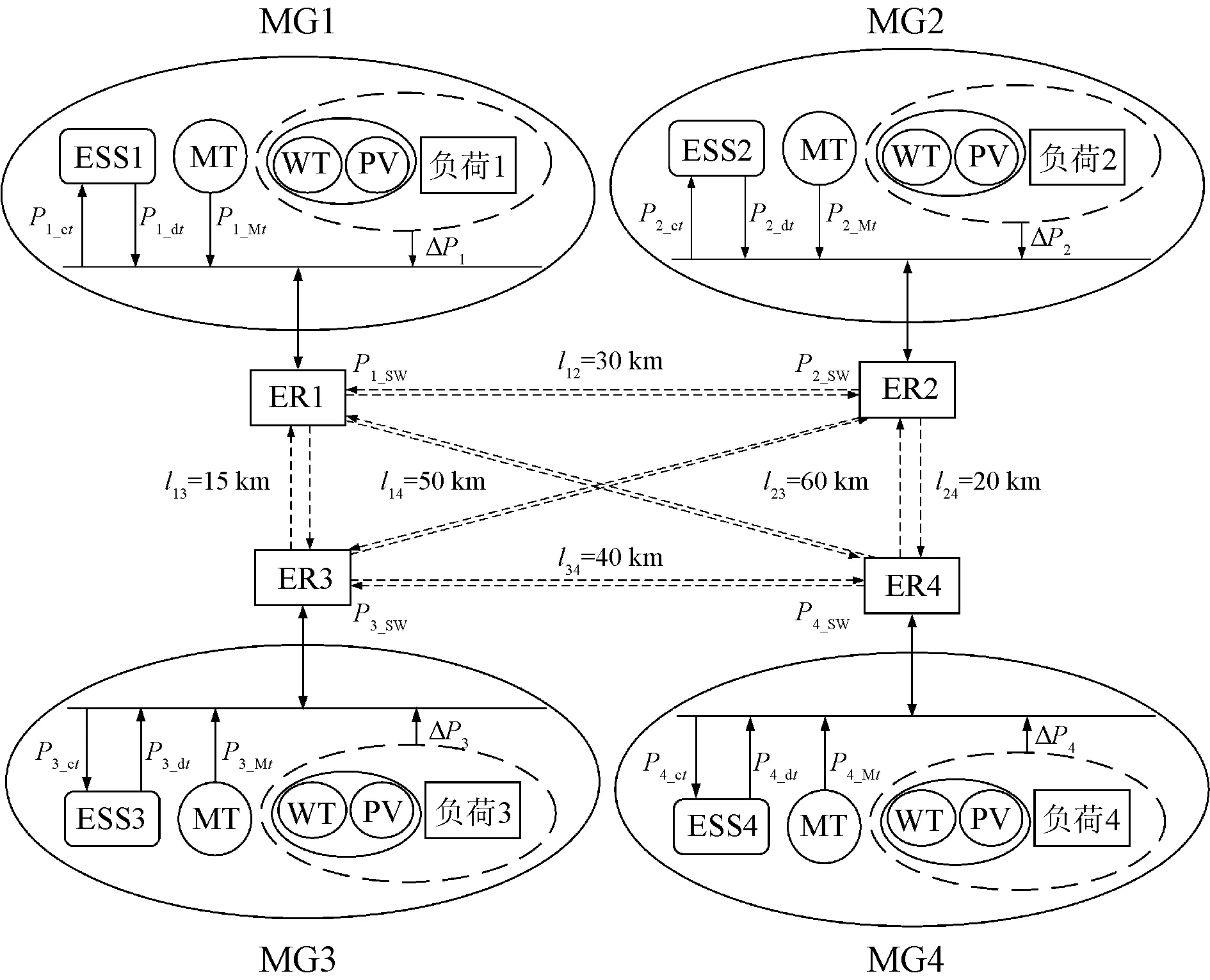
5.2 等级划分策略性能验证和分析


6 结论
