考虑主、散索鞍耦合效应的索鞍预偏量改进算法

邓小康，张 其

(武汉科技大学 汽车与交通工程学院，湖北 武汉 430065)

在悬索桥空缆状态下，如果主、散索鞍不预偏，索鞍两侧将会存在巨大的不平衡力，在索塔底部产生很大的弯矩，影响桥梁结构安全[1-2]。因此主、散索鞍预偏量的确定对于保证悬索桥的施工安全具有重大意义[3-4]。

对于悬索桥索鞍预偏量的计算，许多学者提出了不同的算法，主要有数值解析法和非线性有限元法。相对于非线性有限元法，数值解析法能够考虑更多细节因素，求解更为精确，计算量较小，收敛速度快。本文主要研究数值解析法求解索鞍预偏量，文献[5]先对每个鞍座的预偏量假定一个初值，然后计算各索鞍两侧的主缆线形及主缆内力的不平衡分力，再由不平衡力和索鞍滑移刚度的关系求得预偏量的调整值，不断循环使索鞍两侧的主缆内力达到平衡。文献[6]则先给每个索鞍预偏量赋初值，计算索鞍不平衡力系数，再给索鞍预偏量以不同的增量，调整索鞍不平衡力系数，使其精度满足要求。上述两者都是对预偏量赋初值，并且通过迭代不断调整初值使得索鞍的受力满足要求最终求得预偏量。方法所不同的只是对初值迭代调整的方法存在差异，两种方法在考虑主、散索鞍的耦合效应时需要不断试算主、散索鞍的平衡条件，由此计算出主、散索鞍的预偏量，存在运算复杂，迭代效率较低的问题。文献[7]以成桥状态的不动点间无应力长度为计算条件，对空缆状态下索鞍受力进行分析，建立了主索鞍及主缆的11个非线性方程组，解方程组得出主索鞍的预偏量。文献[8]通过主缆线形基本方程、无应力长度不变、高差闭合条件得出空缆线形从而得出主索鞍的预偏量。文献[7-8]虽然推导出了主索鞍偏移的非线性方程组，都是针对主索鞍预偏量的算法，没有考虑散索鞍和主索鞍偏移之间的耦合关系。

基于此，本文提出了一种索鞍预偏量计算的改进算法，算法考虑主索鞍和散索鞍的耦合效应，对索鞍和主缆进行分析，利用索鞍两侧平衡条件和变形相容条件建立方程组[9-10]，采用牛顿-拉斐森迭代算法求解非线性方程组得到主、散索鞍的预偏量，方法具有计算过程简便，收敛性好的特点。

1 主缆受力分析[11]

本文在前期研究过程中，推导了悬索桥主缆线形的统一悬链线方程和无应力索长计算公式。

主缆线形计算模型及索段划分示意见图1。图1中，主缆以最低点o为原点建立坐标系，y轴竖直向上，左边x轴水平向左，右边x轴水平向右。假定在无应力状态下主缆的横截面面积为A0，沿索长均布的主缆自重荷载为q0；在有应力状态下，主缆的横截面面积变为A，沿索长方向的主缆自重荷载变为q。设E为主缆所用材料的弹性模量，H为索段上任一点索力的水平分力。

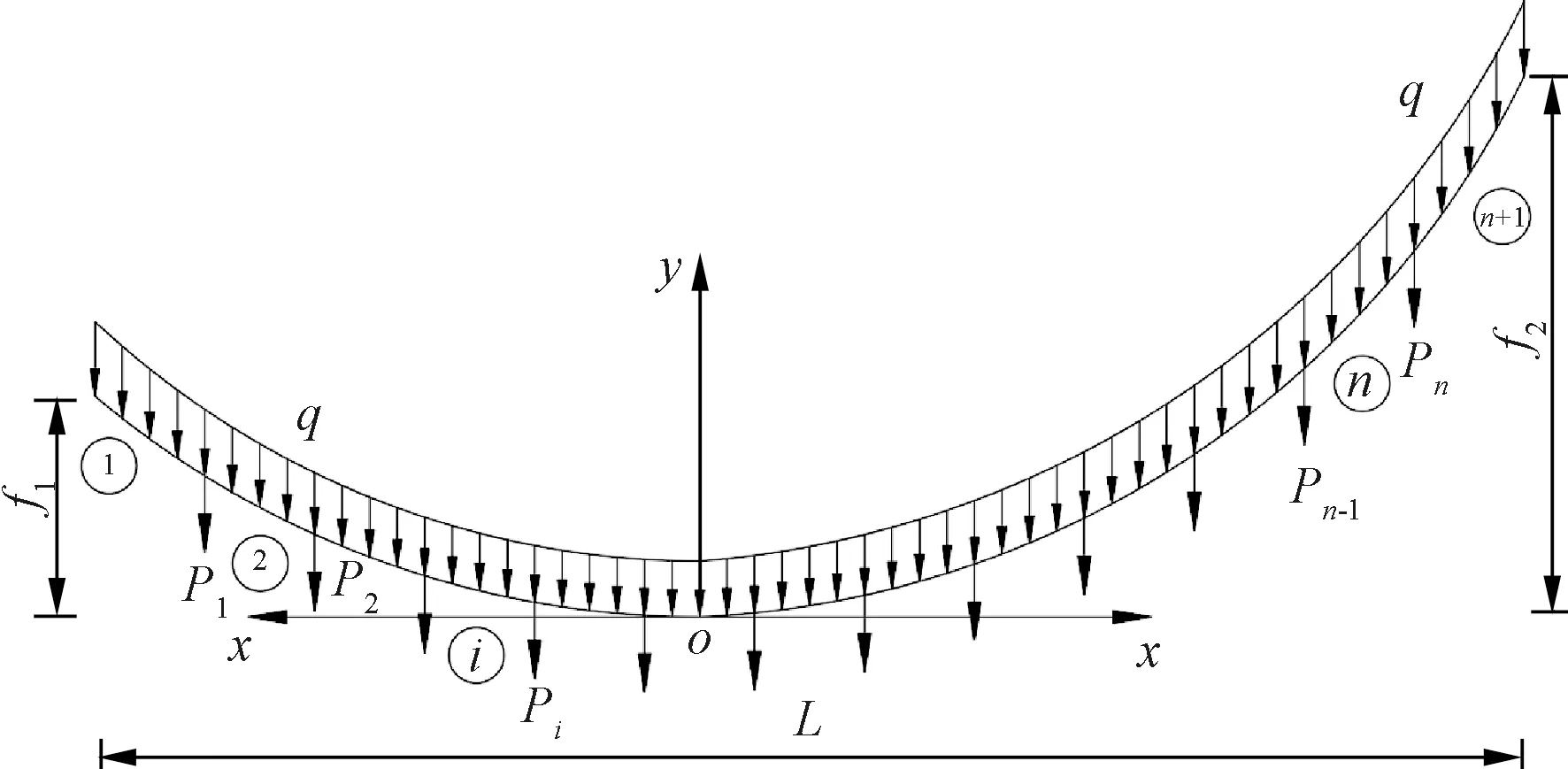
图1 主缆线形计算模型及索段划分示意

则其考虑主缆弹性伸长对主缆自重荷载集度的影响时的主缆线形方程为

(1)

(2)

索段i的无应力索长为

(3)

式中：zH(i)为索段i最高点的斜率；zL(i)为最低点的斜率。

2 主、散索鞍平衡条件的选取

索鞍预偏是为了使空缆状态下索鞍两侧保持一定的平衡关系。

文献[12]对索鞍处的理想平衡条件进行了详细分析，其认为主索鞍的平衡条件有两侧主缆索力相等、主缆索力水平分力相等、主缆沿鞍座滑移面的分力相等三种。本文选取桥塔上的主索鞍两侧主缆水平分力相等(由于塔顶水平，对一般主索鞍来说，这样也能保证沿滑移面的分力相等)这个平衡条件。

国内悬索桥散索鞍有摆轴式和滚轴式两种，其结构形式相似，限于篇幅，本文计算和分析时都采用滚轴式散索鞍(滑动式散索鞍)[13]。参照文献[1]，选取散索鞍两侧主缆沿滑移面的分力相等这个平衡条件进行分析。摆轴式散索鞍的计算方法和滚轴式类似，仅是平衡状态时采用的是弯矩平衡[14]。

3 考虑主、散索鞍耦合效应的预偏方程组建立

以单圆曲线索鞍为例，主索鞍和散索鞍预偏量的计算示意图见图2(取对称结构的一半进行分析)。

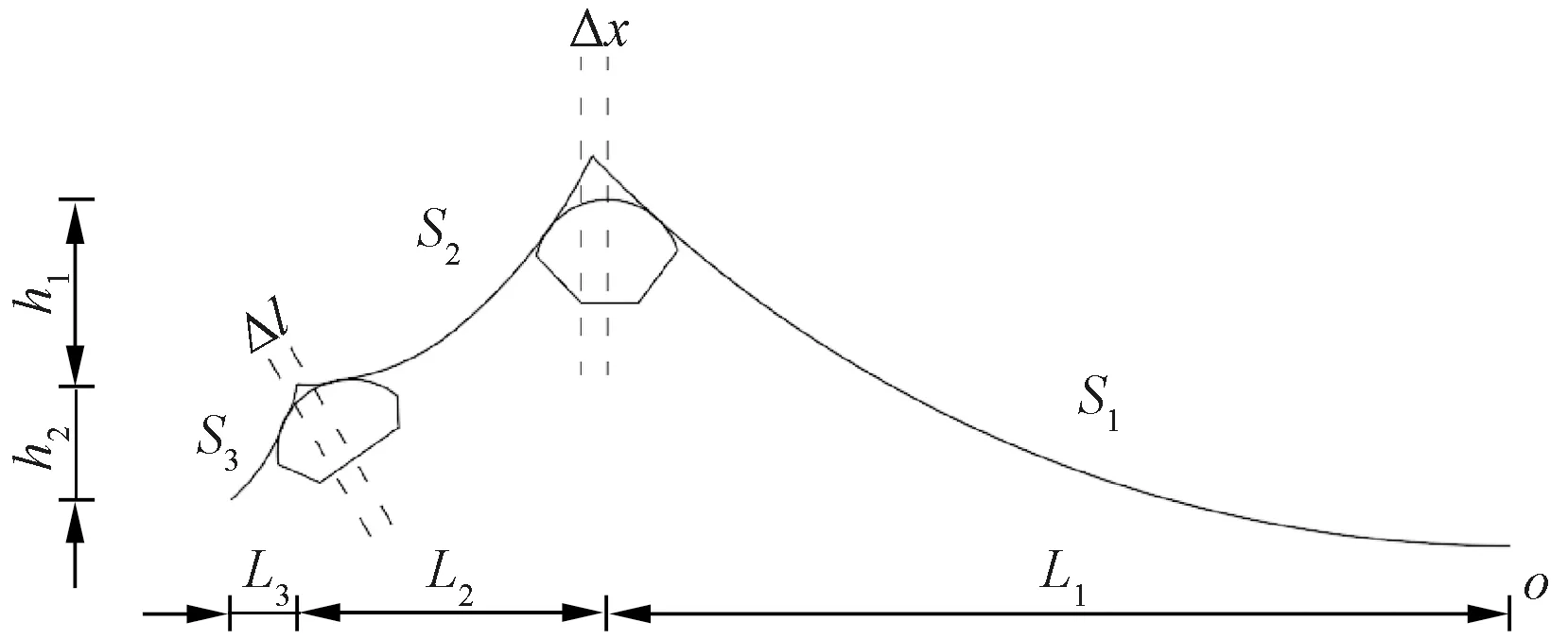
图2 索鞍预偏量计算整体计算示意

计算过程的已知条件可归纳如下：

(1)成桥状态下主跨主索鞍不动点至跨中的水平距离L1，该段主缆无应力长度S1，主索鞍不动点和圆心连线与过圆心铅垂线的夹角γ1，主索鞍的半径为R1。

(2)成桥状态下边跨主索鞍不动点至散索鞍不动点水平距离L2、竖直距离h1，该段主缆无应力长度S2，散索鞍不动点和圆心连线与过圆心铅垂线的夹角γ2，散索鞍的半径为R2。

(3)成桥状态下锚跨散索鞍不动点至锚固点的距离L3、竖直距离h2，该段主缆无应力长度S3，散索鞍滑移面的角度φ。

全桥未知参数共有10个，分别为：

空缆状态下主索鞍主跨侧切点斜率z1、主索鞍边跨侧切点斜率z2、散索鞍边跨侧切点斜率z3、散索鞍锚跨侧切点斜率z4、主缆锚固点斜率z5，空缆状态下主缆主跨段水平张力H1、边跨段水平张力H2、锚跨段水平张力H3，与成桥状态相比空缆状态主索鞍的偏移量Δx，散索鞍沿滑移面的偏移量Δl。参数示意见图2、图3。

图3 主索鞍、散索鞍参数示意

将角度均表示为弧度的形式，对主跨有

R1(sinγ1+sinarctanz1)=L1+Δx

(4)

(5)

同理，对边跨有

R1(cosγ1-cosarctanz2)+R2(cosarctanz3-

cosγ2)=h1+Δlsinφ

(6)

sinγ1)+R2(sinγ2-sinarctanz3)=

L2+Δlcosφ-Δx

(7)

R2(γ2-arctanz3)=S2

(8)

对锚跨有

R2(cosγ2-cosarctanz4)=h2-Δlsinφ

(9)

sinarctanz4)=L3-Δlcosφ

(10)

(11)

对主索鞍和散索鞍的平衡条件为

H1=H2

(12)

H2(cosφ+z3sinφ)=H3(cosφ+z4sinφ)

(13)

需要注意的是，以上主缆与索鞍之间的几何关系可能会随着索鞍的半径有所变化。编制程序时，可通过求得的索鞍切点、圆心之间的关系进行选择判断。

式(4)～式(13)共10个方程，组成一个10元非线性方程组，解出方程组即可得满足节平衡条件的空缆线形及索鞍偏移量，可采用牛顿-拉斐森迭代法求解该方程组。

4 利用牛顿-拉斐森算法求解索鞍预偏方程组

4.1 解索鞍预偏方程的牛顿-拉斐森算法

将式(6)～式(15)改写为

fi(x1，x2，…，x10)=fi(z1，z2，z3，z4，z5，

H1，H2，H3，Δx，Δl)=0i=1，2，…，10

(14)

用向量X记以xi为分量的矢量，F记以fi为分量的矢量，则在某一X连续的邻域内，将fi的Talor级数展开为

fi(X+δX)=

(15)

式中：O(δX2)为高阶微量，可忽略。式中的偏导数构成的矩阵为Jacobi矩阵，可知

(16)

则可得迭代公式为

(17)

Xk=Xk-1+δXk

(18)

式中：k为迭代的次数。

本文编程计算过程如下：

Step1选取初值X0，X0为

(19)

设定求解的精度ε，同时给k赋值k=1。

Step2计算Di=-fi(Xk-1)，i=1，2，…，10，当max|Di|≤ε并满足约束条件时，则方程的解为

(20)

则Step2计算结束。当不满足精度要求时，进入Step3。

Step3由式(16)计算Jacobi矩阵，并由式(17)计算调整值，由式(18)计算调整后的X。重复上述步骤，直至精度满足要求为止。

主、散索鞍预偏量算法流程见图5。

图5 主、散索鞍预偏量算法流程

如此，便求出了空缆状态下主索鞍和散索鞍的预偏量，上述计算过程同时还求出了空缆状态下主缆的线形和内力。

4.2 Jacobi矩阵的推导

对式(4)～式(13)，令矩阵F中的元素分别为

R1(sinγ1+sinarctanz1)-L1-Δx

(21)

(22)

R2(cosarctanz3-cosγ2)-h1-Δlsinφ

(23)

R1(sinarctanz2-sinγ1)+R2(sinγ2-

sinarctanz3)-L2-Δlcosβ+Δx

(24)

R2(γ2-arctanz3)-S2

(25)

R2(cosγ2-cosarctanz4)-h2+Δlsinφ

(26)

L3+Δlcosφ

(27)

(28)

F9=H1-H2

(29)

F10=H2(cosφ+z3sinφ)-

H3(cosφ+z4sinφ)

(30)

由式(18)可得Jacobi矩阵为

J=[Jij]10×10

(31)

式中：

(32)

(33)

0 0 -sinφ]

(34)

(35)

(36)

(37)

(38)

(39)

J9j=[1 -1 0 0 0 0 0 0 0 0]

(40)

J10j=[0 0H2sinφ-H2sinφ0 0 cosφ+

z3sinφ-(cosφ+z4sinφ) 0 0]

(41)

4.3 初值X0的选取原则

在采用牛顿-拉斐森迭代法求解非线性方程组时，初值的选取非常重要，当初值偏离真实解太远时，计算过程甚至有可能不收敛。

本文采用如下方法选取计算初值：

按成桥状态索鞍的位置求解出成桥状态下主缆的线形和内力，分别将此时主、散索鞍两边切点的斜率和锚固点的斜率作为z1、z2、z3、z4、z5的初值，将此时主缆在各段的水平张力作为H1、H2、H3的初值，主索鞍偏移量Δx的初值可取为1.0 m，散索鞍沿滑移面偏移量Δl的初值可取为0.1 m。再采用同伦延拓法帮助牛顿拉斐森算法产生一个好的初值，以降低初值选取对牛顿-拉斐森迭代法收敛性的影响程度。

因此构造H(X,s)函数为

H(X,s)=Hi(x1，x2，…，x10，s)=

sF(X)+(1-s)F0(X)i=1，2，…，10

(42)

式(42)中s的取值范围为[0，1]，且F(X)函数与原函数F0(X)同伦。

F0(X)=F(X)-F(X0)

(43)

式(43)中X0即选取的初值，将式(43)代入式(42)可得

(44)

此时，H(X，s)函数与F(X)函数导数相同，在牛顿迭代过程中，用构造函数H(X，s)代替F(X)。计算结果表明，这样设置，一般可保证方程组快速收敛。

5 算例

某悬索桥主缆横截面面积为1.488 m2，主缆钢材的弹性模量E=2.0×105MPa，2根主缆沿索长均布的自重荷载集度之和为116.03 kN/m。主索鞍、散索鞍的曲线半径分别为10.57、7.5 m。成桥状态下主跨侧主缆在主索鞍不动点与主跨跨中之间的无应力长度为870.976 45 m,水平距离为849.972 9 m，主索鞍不动点和主索鞍圆曲线圆心连线与过圆心铅垂线的夹角为0.024 184 46 rad。成桥状态下边跨侧主缆在主索鞍不动点与散索鞍不动点之间的无应力长度为510.043 6 m，水平距离为465 m，高差为220.3 m，散索鞍不动点和散索鞍圆曲线圆心连线与过圆心铅垂线的夹角为0.140 656 345 rad。成桥状态下锚跨侧主缆在散索鞍不动点与锚固点之间的无应力长度为32.478 8 m，水平距离为25.279 5 m，竖直距离为21.212 0 m，散索鞍滑移面的倾斜角为31.961 5°。

按成桥状态索鞍的位置计算得出主缆的线形和内力，得到H1=248 126.1 kN，H2=994 935.83 kN，H3=833 210.26 kN，z1=0.405 118 89，z2=0.443 865 33，z3=0.444 249 17，z4=0.841 218 73，z5=0.836 818 85。

将此时的z1、z2、z3、z4、z5、H1、H2、H3作为初值，Δx的初值取为1 m，Δl的初值取为0.1 m，代入程序中计算得到的结果与采用文献[6]的计算结果对比见表1。

表1 索鞍预偏量的计算结果

由表1可知，采用本文方法计算得出的主索鞍和散索鞍预偏量和采用文献[6]方法计算的结果基本一致，但文献[6]方法在计算过程中需要不断试算主、散索鞍的平衡条件，计算繁琐。由表1还可以看出，采用本文方法和文献[6]方法计算出的索鞍预偏量均能满足主、散索鞍的平衡条件。

6 结论

(1)本文提出一种考虑主、散索鞍耦合效应的索鞍预偏量改进算法。算法基于对主缆和索鞍的力学及几何关系分析，推导出一个十元非线性方程组，采用牛顿-拉斐森法求解方程组，即可同时得到主、散索鞍的预偏量，力学概念清晰，求解简单。

(2)本文还给出了牛顿-拉斐森法求解方程组时初值的选取方法。按成桥状态索鞍的位置求出各点斜率以及水平分力，由此作为斜率和水平分力的计算初值，主索鞍偏移量的初值可取为1.0 m，散索鞍沿滑移面偏移量的初值可取为0.1 m。这样设置，一般可保证算法快速收敛。

(3)算例表明，本文方法计算出的索鞍预偏量满足索鞍平衡条件的要求，计算精度较高。该算法适用于平面缆索悬索桥索鞍预偏量的计算。