基于星座点聚类和变换模式匹配的定时同步算法
2022-04-01刘一非张在琛范逸风张志轩
刘一非,吴 亮,2,张在琛,2,党 建,2,范逸风,张志轩
(1.东南大学 移动通信国家重点实验室,江苏 南京210096;2.网络通信与安全紫金山实验室,江苏 南京211111;3.南京电子设备研究所,江苏 南京210000)
0 引言
定时同步技术是通信系统中的关键技术之一[1]。在通信系统中,定时同步技术是指接收端通过帧结构确定每一帧的起始位置,是接收端数据处理的重要步骤,只有做到精确的同步才能保障后续频偏估计、均衡相位补偿、解调的正确性[2]。传统的同步算法利用同步序列的互相关特性搜索峰值,从而估计得到同步点。但是,传统的同步算法容易受频偏、噪声和信息相关性的影响,同步性能有进一步提升空间。
智能反射面(Reconfigurable Intelligent Surfaces,RIS)技术被认为是未来移动通信的关键技术之一[3-4]。基于RIS的通信系统利用反射面的反射相位来调制单频信号,这颠覆了传统的由发射机对基带信号调制的方式[3]。另外,通过适当地调整RIS元素的系数,反射面反射的信号可以与来自其他路径的信号建设性地相加,以增强接收机处的期望信号功率,也可以消除诸如同信道干扰等不期望信号,提高能量利用效率[5-6]。
在基于RIS的通信系统中,传输信息通过计算机和现场可编程逻辑门阵列(Field Programmable Gate Array,FPGA)开发板输出控制电压,调控RIS的反射相位,单频载波信号指向RIS并经过相位调制反射到无线信道[7]。然而一般反射面的调制星座点具有幅度不均衡性,例如在正交相移键控(Quadrature Phase Shift Keying,QPSK)调制中,4个相位的星座点的幅度并不容易调控一致,这对传统定时同步算法性能影响极大[8]。精确控制星座点需要一定的复杂度成本,并且不同RIS表现的调制特性也不一样,这时候更高性能的同步算法就更加重要。
调制星座点在聚类上的清晰划分为解决定时同步问题提供了思路。尽管星座点并非幅度准确的,聚类算法却可以将它们划分至不同的簇[9],利用这一划分结果可以提取出星座点的变换模式,并与已知的同步序列的变换模式做本地相关,由此可以确定同步点。由于聚类实现了数据的锐化,所提同步算法的同步结果呈现锐利的峰值,相较于传统的同步算法更加准确,其准确性在仿真和实际系统中得到了检验。
1 基于RIS调制的通信系统模型
基于RIS的传输系统框图如图1所示。

图1 基于RIS的通信系统框图Fig.1 Diagram of the RIS based communication system
发射端由信号发生器、RIS、FPGA开发板和计算机组成。待传输的信息在计算机Matlab程序中进行编码、组帧、生成比特流、映射到QPSK符号并向FPGA开发板输出控制信号,FPGA根据控制信号对RIS控制每个单元的相位进行调控。与此同时信号发生器通过天线发射单音载频信号给RIS,经过反射面的相位信息调制,最终输出到无线信道[10],发射端数据处理流程如图2(a)所示。
接收端由接收天线、通用软件无线电外设(Universal Software Radio Peripheral,USRP)、计算机组成。接收端数据处理流程如图2(b)所示,接收天线接收无线信道传输的信号,在集成的USRP模块中根据LabView程序预设参数进行高频采样、下变频、多倍抽取采样,并将采样值传给PC的LabView程序进行同步、频偏估计、均衡、解调、帧拼接、显示传输图片。
设计一帧长度为Lbit,一帧中前2L1bit为同步序列(本文采用2个相同的伪随机(Pseudo-Noise,PN)序列作为同步序列),L2bit为帧序号,后L3bit为信息部分。每2 bit映射到一个QPSK符号,[bit2i-1,bit2i]分别表示第2i-1和第2i位的数字。符号映射关系如式(1)所示,帧结构设计如图3所示。
(1)

(a) 发射端数据处理流程
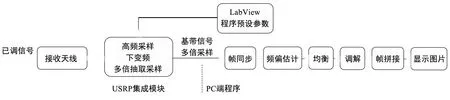
(b) 接收端数据处理流程图2 发射端和接收端数据处理流程Fig.2 Data processing flow diagram of the transmitter and the receiver

图3 帧结构Fig.3 Frame structure
2 传统互相关定时同步技术及缺点
定时同步是接收端通过帧结构确定每一帧的起始位置,是接收端数据处理的重要步骤,只有做到精确无误的帧同步才能为后续频偏估计、均衡相位补偿、解调正确性提供保障。同步算法利用导频,即两个相同的PN序列,计算得到同步点,也为后续相位补偿、解调提供重要依据。
2.1 基于滑动窗互相关的定时同步技术
传统定时同步是利用两个相隔固定距离的滑动窗,通过搜索两个窗内采样之间的相似度判断当前位置是否为帧头部。对于本系统设计的帧结构,两个滑动窗W1、W2的间隔为0,滑动窗长度为L1/2个符号,即单个导频序列PN的长度,起始位置为δ,在采样符号y(n)中依次滑动。当W1与一帧中的的起始PN部分重叠时,两个窗内L1/2个符号采样块之间的相似度达到最大[11]。所以在两个滑块数据差的最小点就是帧起始点,即
(2)
也可以用W1的数据和W2共轭相乘的最大值点来判断帧起始点:
(3)
2.2 传统互相关定时同步技术的缺点
在帧长度较短的情况下,传统帧同步的主要缺点是受频偏、信道噪声或是信息部分message相关性影响较大[12-13],不能准确找到同步点。例如上述算法中,滑动W1和W2共轭相乘的模值分布如图4所示。在正确同步点周围位置点的相似度比较接近甚至大于正确同步点的相似度,出现该现象的原因有频偏、信道噪声的影响以及信息Message结尾部分和PN起始部分有相关性等[14]。

图4 传统同步算法的不准确Fig.4 Inaccuracy of the traditional synchronization algorithm
3 星座点聚类及其辅助的定时同步算法
前述部分的问题焦点在于随机噪声对相似度函数值的影响,相似度函数乘积式相加的形式容易受到随机噪声影响,继而使得同步点处的相似度不够锐利,峰值不够突出甚至没有峰值。但可以观察发现,尽管有噪声影响,PN符号可以非常清楚地聚类为4类,即对应QPSK的4个相位。受Sigmoid函数启发,可以将两个PN序列组合作为同步序列,共L1个符号,将其中每一个符号归为一种模式,与本地的PN符号模式比较,锐利化后再相加作为相似度函数。
但此时存在相位差影响,且聚类结果不可同于传统共轭相乘作法,相位差无法作为公因子取模后消去,未知的相位差使得接收到的PN序列与本地PN序列无法进行匹配。
但无论星座点如何旋转,星座点之间的变化方向不会改变,所以星座点的变换模式可以进行匹配。当采用QPSK调制时,从一个星座点到下一个星座点的变换模式分为不变、逆时针、对角线、顺时针4种,这就为模式匹配提供了依据。
3.1 聚类算法
3.1.1 Kmeans聚类算法
Kmeans聚类算法的主要思想是,给定聚类的数量K,选择K个类簇中心初始点,将每个采样点根据判定距离分配到最近的类簇中,并更新每一个类簇的质心(中心点),重复上述步骤直到每个类簇的质心不再变化或迭代次数达到指定数值[9]。Kmeans星座点聚类算法伪代码如算法1所示。

算法1 Kmeans星座点聚类算法伪代码输入:样本星座点集D=x1,x2,…,xN{},类簇数k=4。从D中随机选择k个样本作为初始均值向量μ1,μ2,…,μk{}初始化簇集合Ci=φ(i=1,2,…,k)Repeat forj=1,2,…,N do 计算星座点与各类簇中心点μi(i=1,2,…,k)的距离:dji=xj-μi2 找到离xj最近的簇中心点:λj=argmini∈1,2,…,k{}dji 将星座点xj分配给最近的簇:Cλj=Cλj∪xj{} end for fori=1,2,…,k do 计算新均值向量μi=1Ci∑x∈Cix end forUntil 当前均值向量未更新输出:簇划分C=C1,C2,…,Ck{}
在实际操作中,发现Kmeans聚类的稳定性比较差,非常依赖初始聚类点的选择。如果初始点有两个或多个选在同一聚类中的点,称为竞争点,迭代过程中就容易出现某一中心点的聚类为空集的情况,因为本该属于该类的点被分配给了初始时的其他竞争点,导致迭代不能进行下去。此外,Kmeans聚类还会出现伪收敛,即采样点被分为4类并且满足4个均值点不再变化的迭代终止条件,但是分类情况明显不满足QPSK的相位分布,用机器学习的方法而不是从实际的数理规律出发有其明显的局限性[9,15]。
3.1.2 基于相位分布的聚类算法
QPSK调制下可以单从相位分布角度来实现聚类,从二维的距离判决转换为一维的相位角度判决,降低了聚类的复杂性。另外,注意到对于按照相位排序的采样点,从一类到另一类的相位跨度值很大,例如在90°附近,QPSK有三处大角度跨越。因此,基于相位分布聚类算法的主要思想是,将采样点按相位排序,计算排序后序列相邻两点的相位差,取相位差前三大的位置为类间跨越的位置,并以此为间隔将采样点分为4类。

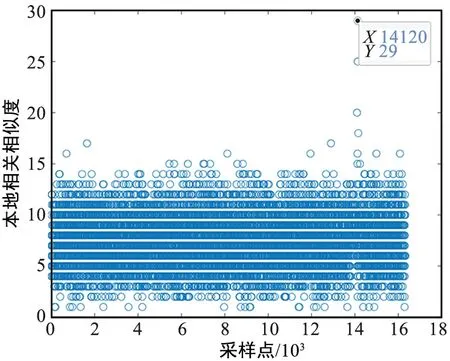
算法2 基于相位分布的聚类算法的伪代码输入:样本星座点集D=x1,x2,…,xN{},类簇数k=4。取样本星座点相位,并按从小到大排序: ang=angle(D),angsort=sort(ang)如果有同一类星座点落在180°轴两侧,调整星座点:if angsort(1)+2π-angsort(N)<π18 then 星座点旋转45°:D=D·ejπ4 重新取相位并排序:ang=angle(D),angsort=sort(ang)end iffor i=1:N-1 计算排序后相邻相位的差值:da(i)=angsort(i+1)-angsort(i)end for差值矩阵中前三大的点作为类间跨越点,取其下标: index=find the index of max 3 numbers of da将三个类间跨越点的相位分别作为相位判决门限: gate=angsort(index)初始化簇集合Ci=φ(i=1,2,…,k)fori=1:N if ang(i) 需要特别注意的是,由于取复数相位的函数angle()范围在[-π,π],初始时需要将星座点标准化,即对星座点整体逆时针旋转一定角度,避免同一类星座点坐落在180°轴两侧,以适配聚类算法,基于相位分布的聚类算法的伪代码如算法2所示。 利用基于相位分布的聚类算法可得到星座点聚类结果如图5所示,从图中可以看出星座被有效地分为4类。 图5 部分采样星座点的聚类结果Fig.5 Clustering results of the constellation points 对于QPSK符号,每个星座点xi到下一个星座点xi+1的变换分为4种模式:不变、逆时针、对角线、顺时针,如图6所示。 图6 从一簇星座点到其他簇的变换模式Fig.6 Transform pattern from one cluster to another cluster 定义这4种变化模式为模式0、1、2、3。前文可得每个星座采样点的聚类结果,设xi∈Cm,xi+1∈Cn,且1类、2类、3类、4类是按照逆时针顺序,定义变换模式矩阵 (4) 则从Cm到Cn的变换模式为shiftmn。 本算法中不再利用互相关,因此可以将2个PN序列合在一起作为同步序列。在滑动搜索过程中,长度为L1sym的滑块在采样点上滑动,滑块起始于采样点xk时,可以定义第k个变换模式向量 dsk=[dsk,dsk+1…dsk+L1-1], (5) 其中,dsi表示(xi→xi+1)的变换模式。同理可得同步序列PN的变换模式向量dr=[dr1,dr2…drL1-1],其中,dri表示同步序列的第i个符号到第i+1符号的变换模式。定义第k个变换模式向量的相似度函数为: (6) 其中, (7) 移动滑块并搜索,相似度Sk最大的点即为同步点,即: (8) 值得注意的是,虽然在同步算法分析的过程中以QPSK为例,但是本文提出的基于星座点聚类和变换模式匹配的同步算法同样适用于其他的调制算法。 仿真过程中的具体参数设置如表1所示,同步序列包含2个PN序列共60 bit,即30个星座采样点,可以得到长度为29的变换模式矩阵。将接收信号的PN变换模式与本地的PN变换模式做匹配,即可得到相似度函数,如图7所示。在帧起始位置,即PN位置处的相似度为29,呈现非常锐利的峰值。 表1 仿真算法中参数设置 图7 基于星座点聚类和变换模式匹配的相似度函数Fig.7 Similarity function based on constellation clustering and transform pattern matching 如图8所示,两种同步算法下,平均同步点和理论值的误差都随着信噪比的增大而减小,传统滑动相关同步算法的误差稳定高于0.5,本文提出的基于星座点聚类和变换模式匹配算法的误差始终小于传统算法,并且在信噪比大于9 dB之后平均误差为0,即可以精准实现同步。 图8 传统同步算法和本文提出算法的同步性能对比Fig.8 Synchronization performance comparison between the traditional synchronization algorithm and the proposed algorithm 实际搭建的基于RIS的QPSK通信系统如图9所示,包括发射端和接收端,其中RIS位于发射端。实测系统参数设置如表2所示。 图9 基于RIS的通信系统发射端和接收端实验设备Fig.9 Experimental equipments of transmitter and receiver in the RIS-based communication system 表2 实测RIS通信系统参数设置 接收端Labview前面板显示数据处理结果如图10所示。如图10(a)所示,同步点处相似度函数呈现锐利的峰值,可以精确找到同步点。如图10(b),时频同步处理后一帧中的星座点可以清晰划分为4簇,解调后的图片如图10(c)所示,可以正确解调出发射的图片。 (a) 实际系统中的相似度函数 (b) 时频同步后一帧数据的星座图 (c) 解调出的图片 本文提出了一种基于星座点聚类和变换模式匹配的同步算法,有效解决了传统同步算法易受频偏、噪声和信息相关性影响的问题。本文提出的同步算法使用聚类方法提取出导频星座点的变换模式,有效锐化了匹配度函数的峰值,极大提高了同步的准确性。在仿真和实测系统中,提出算法的同步结果均可靠准确。
3.2 星座点变换模式匹配
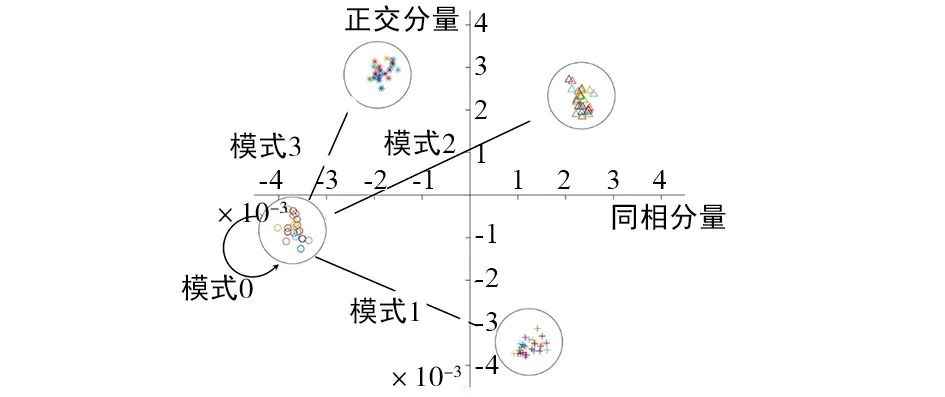


4 仿真和实测结果
4.1 仿真结果


4.2 实际系统结果





5 结论
