基于蚁群算法的无人机侦察任务分配
2022-04-01马培博
马培博,钟 麟
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
在现阶段的对抗场景中,空中力量的强弱往往对结果起到了关键性作用[1]。其中无人机在训练过程中不需要飞行员参与空中训练,大大节省费用的同时也避免了人员伤亡;并且无人机的地勤保障要求较低,无需大规模的起降场地,因而机动性较强[2-3]。鉴于无人机具备上述优势,在战场侦察任务中起到了至关重要的作用,且未来战场中利用无人机执行侦察任务将是必然的发展趋势[4]。
侦察任务分配本质是一个指派问题,根据目标的特点指派符合要求的侦察无人机。在当前多数研究中,将该问题抽象成旅行商问题或车辆路径问题等,然后利用智能算法进行求解[5-6]。而在实际应用中,上述模型缺乏一定的约束条件,将有可能产生无效的分配方案。如不同的目标所需的机载设备不同,若不考虑负载匹配将可能给无人机分配一个无法进行侦察的目标;不同的无人机其性能也不尽相同,若将距离较远的目标分配给剩余航程较短的无人机将会造成无人机半路返航甚至坠毁。
本文在聚焦实际侦察任务特点的基础上,充分考虑所需的约束条件,建立了无人机任务分配模型。针对所建立模型和任务分配问题的特点,选用蚁群算法作为模型的求解算法,设计了无人机侦察任务分配算法,并通过仿真实验验证了该算法的有效性和实用性。
1 侦察任务分配问题模型设计
本文针对的应用背景为静态任务分配,即待解决问题的场景为静止状态,无人机和侦察目标的数量、位置属性等均已确定且在一定时间内保持不变[7]。通过本文算法将场景中存在的无人机与侦察目标进行匹配,得到侦察任务分配方案。在进行分配时,按照最小代价准则、放弃分配准则和最大分配率准则进行分配,得到无人机侦察任务分配问题的数学模型如下:
(1)
式(1)是将目标分配方案的整体代价值f最小作为优化目标函数,根据放弃分配准则和最大分配率准则设定了约束条件。目标函数中DCost为该方案中无人机执行任务所需的飞行航程,根据场景模型中无人机和目标的位置,可以计算出各无人机与目标间的距离。无人机i到目标j的距离即为分配方案(i,j)的航程代价:
DCost(i,j)=D(Ui,Tj)=‖Ui,Tj‖,
(2)
式中,i1、i2分别为无人机位置的横纵坐标,j1、j2分别为目标位置的横纵坐标。
目标函数中TCost为该分配方案所需的耗时,给无人机分配侦察目标时,需要飞行到达目标所在位置,因而会付出相应的时间代价,即各无人机的飞行时间。
(3)
式中,D(i,j)表示无人机i到目标j的距离,speed(i)为无人机i的飞行速度。由于航程和时间的量纲不同,因此加入调整因子α、β来调整二者的权重。
λ为方案违反约束条件时加入的惩罚因子,本文设定的约束条件包括航程约束、载荷约束和时间约束。在场景模型中对每个无人机均设定了最大航程,在比较分配方案时需要判断完成侦察任务所需的飞行距离是否超过了该平台的最大航程。若超出了最大航程,则需要在该分配方案的代价值中加入航程约束的惩罚因子DSin。
(4)
式中,DCost(i)为平台i完成所有侦察任务所需的飞行距离,maxDis(i)为平台i的最大航程。
同理,在场景设定中,对每个无人机也设定了最大飞行时间。为避免分配方案中出现无人机耗时过大的情况,在比较分配方案时需要判断完成侦察任务所需的时间是否超过了该无人机的最大飞行时间。式(5)为无人机最大飞行时间的计算公式。当分配方案的总耗时大于无人机的最大飞行时间时,则需要在该分配方案的代价值中加入时间约束的惩罚因子TSin。
(5)
(6)
无人机可携带的侦察装置种类多样,可以搭载电子侦察设备进行通信侦察,携带航空照相机进行拍摄,也可以搭载可见光、红外等光电侦察设备,部分无人机也装有实时情报处理和传输设备,这就决定了不同的无人机可匹配的侦察目标不同[8]。因此,对分配方案需要判断是否满足载荷要求,将场景中设定的无人机载荷与匹配的目标所需的载荷类型进行对比,若二者存在匹配的载荷,表示该分配方案满足载荷要求,否则将对该方案加入载荷约束的惩罚因子LSin。
(7)
式中,TNeed为目标所需的载荷种类集合,PLoad为无人机携带的载荷种类集合。只有当PLoad中存在TNeed中的元素时,才能保证该匹配关系能够满足载荷要求。
2 算法设计
2.1 蚁群算法原理
蚁群算法是一种启发式智能算法,属于集中式算法。该算法是由学者根据自然中蚁群觅食规律提出的一种仿生算法[9]。蚁群算法中每个蚂蚁个体通过计算各路径的转移概率后选择转移方向,并根据总路径长度释放相关的信息素。该算法最早应用于旅行商问题,也可以用于解决指派问题、路由问题等。
在自然界中,科学家发现蚂蚁在行走过程中可以在地面上沉积一种化学物质,并且该物质可以被其他蚂蚁个体识别,称之为信息素[10-11]。蚂蚁个体在完成一次完整的巡游后,会通过释放信息素来标记出完整的路径,并且释放信息素的浓度与该路径长度成反比,当其经过的路径越短,释放的信息素越大;反之,则释放的信息素越小[12]。当后续蚂蚁个体经过未知路径时,可以根据之前蚂蚁留下的信息素进行选择,优先挑选信息素较大的路径,并且后续经过的蚂蚁个体也将释放新的信息素[13]。经此以往,便形成一个正反馈机制,最优路径上的信息素浓度会越来越大,而其他路径上的信息素会随时间的推移而减少,最终可以挑选出最优路径[14]。
2.2 算法实现步骤
将蚁群算法应用于本文的UAV侦察任务分配模型中时,具体的步骤及实现过程如下。
(1) 算法初始化
对蚁群算法中涉及的参数进行初始化设置,参数可分为算法参数和场景参数。算法参数主要包括蚁群规模m、问题规模n,最大迭代次数iter_max、信息素/启发函数重要程度因子α、β和信息素矩阵(τij)m×n等。并将禁忌表tabuk(k=1,2,…,m)设置为空集,代表当前蚂蚁没有已选择的目标;用集合allowk={C-tabuk}表示蚂蚁下一步可以选择的目标集合,C为问题中所有的目标点。场景参数中主要包括无人机/目标的位置、无人机飞行速度、目标所需载荷、无人机载荷和无人机最大航程。根据场景设定,对上述参数进行设置。
(2) 生成蚁群
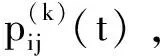
(8)

如蚂蚁个体可表示为:

(9)
其所代表的分配方案中,每个无人机均分得了一个目标,其中1号目标分给2号无人机,4号目标分配给3号无人机,以此类推。
(3) 计算分配方案代价值
生成蚁群后,对每只蚂蚁个体代表的分配方案计算代价值,用方案代价值来表示每只蚂蚁的巡游路径长度。分配方案的总代价值包括无人机的航程代价、执行任务所需的时间代价以及违反约束条件时引入的惩罚因子[16]。
(4) 更新蚁群信息素

(10)
其次根据信息素增量矩阵来更新蚁群的信息素矩阵,计算公式如式(11),其中τij(t+n)为更新后的信息素取值,ρ为挥发因子,τij(t)为更新前的信息素取值。
τij(t+n)=(1-ρ)×τij(t)+Δτij。
(11)
根据上述步骤进行iter_max次循环后,选出代价值最小的分配方案作为本次迭代的最优分配方案,并将该分配方案及最小迭代次数曲线进行展示。
3 仿真实验与结果分析
3.1 仿真实验设计
本文设计的仿真实验场景为8个无人机和8个待侦察目标,在50 km×50 km的范围内进行侦察。表 1和表 2分别为实验中蚁群算法参数取值和场景参数设定。无人机载荷分别用1~4代表了4种不同类型的载荷,当无人机载荷设定为[1 2 3 4]时,表示该无人机可以匹配现有场景中的所有目标;当无人机载荷的取值为其中一种或几种时,表示该无人机只能满足某种特定类型目标对载荷的需求。将场景中航程约束惩罚因子S1、时间约束惩罚因子S2和载荷约束惩罚因子S3的取值设定为相同值,均为100。

表1 蚁群算法参数取值

表2 场景参数取值
进行实验时,先根据上表设定的参数取值获取分配方案。其次,进行两次对比实验,一是改变某些无人机的载荷后,观察载荷约束是否起到作用;二是改变某些无人机的最大航程后,分析航程约束是否起到作用。
3.2 仿真实验结果及分析
根据上述场景设定及实验流程,在Matlab 2012环境中,耗时1.2 s得到侦察任务分配方案及最小代价迭代曲线分别如图 1和图 2所示。
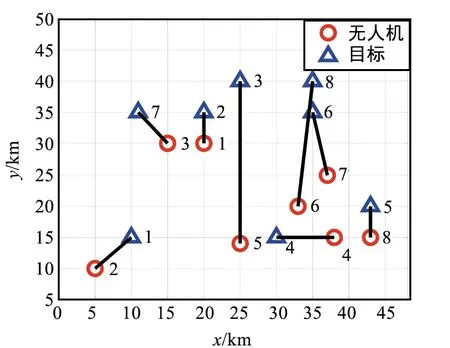
图1 侦察任务分配方案Fig.1 Reconnaissance task assignment plan

图2 最小代价迭代曲线Fig.2 Minimum cost iteration curve
图 1中每个无人机根据自身属性参数选定了一个最适合自身的目标进行匹配,所有无人机与目标均进行了分配。图 2表示该场景收敛曲线,代表每次迭代中计算得到的最小代价值,从最终的分配方案代价值可以看出,该分配方案未违反约束条件,因此,当前获取的侦察任务分配方案为局部最优分配方案。
3.3 载荷约束验证实验及分析
在上述实验的基础上,改变某些无人机的载荷,使其只能匹配某个目标,并增大载荷约束惩罚因子S3取值,使违反载荷约束的分配方案能够被算法过滤,改变后的场景参数取值如表 3所示。

表3 载荷约束验证实验参数取值
根据表 3中载荷的变化,将8号无人机改为携带一种载荷,且只能满足8号目标的需求。从图 5可以看出,改变了原来的分配方案,使8号无人机与8号目标进行了匹配,表明载荷约束起到了作用。并且图 6中迭代次数进一步增大,表明约束条件增多时需要更多的迭代次数来找到局部最优分配方案。

图3 改变载荷后任务分配方案Fig.3 Task allocation after changing load

图4 改变载荷后最小代价迭代曲线Fig.4 Minimum cost iteration curve after changing load
4 结论
根据一对一场景及载荷约束验证场景实验结果分析得出,基于蚁群算法加入约束的无人机侦察任务分配模型能够满足场景需求,能够在约束条件作用下获取局部最优分配方案,更好地贴合实际应用场景。同时通过分析算法实验的耗时,证明该算法敏捷高效,具备可行性和有效性。
