从集中式到分布式的赢者通吃网络：回顾与展望

齐一萌，金 龙

(兰州大学 信息科学与工程学院，甘肃 兰州 730000)

0 引言

一类能够从一组输入信息中选择出最大值的竞争型神经网络被称为赢者通吃(Winner-Take-All，WTA)网络[1]，它是由神经元之间的横向抑制形成的。WTA网络作为k-WTA网络的特例，已被广泛应用于模式识别[2]、联想记忆[3]、多智能体协同[4]以及认知现象模拟[5]等多种领域。Maxnet是传统用于模拟WTA行为的神经网络[6]，它提供了一个离散形式的相互抑制的结构。从数据阵列中选择最大值这一操作在许多领域都是至关重要的，如决策系统和竞争学习网络[7]。为此，国内外学者开展了一系列研究，例如基于自组织算法的迭代神经网络模型，该类模型主要适用于软件实现[8]。输入信息规模的扩张以及计算实时性的要求使得并行方法及可硬件实现的算法备受关注[9]。Lazzaro等人[10]设计了一系列紧凑的互补金属氧化物半导体集成电路来实现WTA行为。Wawryn等人[11]引入一种基于电流源电路的可编程WTA神经网络，并验证了其有效性。然而，以上工作均面向静态WTA问题设计，未考虑实际应用场景的动态特征。进一步地，Majani等人[12]将WTA网络扩展到k-WTA网络，然而只保证了模型的局部稳定性。此后，设计超大规模集成电路来执行k-WTA运算成为一个研究热点[13]。Calvert等人[14]构建了一种Hopfield型神经网络,并通过严格的稳定性分析证明了其能够有效地识别序列中的最大分量。Tymoshchuk[15]根据输入信号的动态移位设计了一个离散k-WTA神经电路，该电路硬件实现复杂度较低，且能在有限的迭代次数内收敛。此后，Tymoshchuk和Wunsch[16]设计了一种有限分辨率的连续k-WTA神经模型，其理论上能够处理未知输入并保证瞬时零误差。Danciu 等人[17]介绍了一种具有O(n2)结构复杂度的递归神经网络，其中n表示输入的数量。然而，该网络需通过将其增益参数设定为无限大以确保k-WTA系统的正确运行。

出于对模型结构的优化，文献[18-19]分别首次实现WTA或k-WTA问题向线性规划(Linear Programming，LP)和二次规划(Quadratic Programming，QP)的转化。进而投影神经网络、对偶神经网络、动态神经网络等被陆续开发并应用[18,20]，同时在多样化激励函数的引入[21]、收敛速率的提升[22]等方面均做出了改进。为进一步简化模型复杂度，多种单状态变量的连续/离散型时间递归神经网络被构建。这些模型[18-22]在处理时不变输入的k-WTA 操作时表现出有限时间收敛性能，但处理时变输入时存在滞后误差，需要通过设置足够大的参数来缓解这一现象。Ferreira等人[23]针对变量有界的LP问题，构造了一个k-WTA神经网络(k-WTA Neural Network，kWNN)，将问题的解转化为所设计神经网络的平衡集，并证明了所构建网络的收敛性。前述研究的k-WTA问题及求解算法均明确指定k的数值，而文献[24]的工作突破了这一限制，提出了一种基于梯度下降法的kWNN模型，实现了k值的动态确定。然而，包含上述工作在内的算法仍存在一些挑战。首先，在处理本质上具有动态特性的问题时，这些方法忽略了内部动态参数随时间的变化趋势，使得它们预测能力不足，从而导致每一时刻所得解与理论解之间存在滞后误差。这种误差是不可忽略的，且会随时间累积影响任务的执行精度。其次，上述神经网络的设计均未考虑去噪措施，因此在噪声干扰下，神经网络的性能会显著下降。而在实际的k-WTA问题求解过程中，干扰是不可避免的，这一定程度上限制了现有算法在复杂环境中的应用。鉴于此，作者已有的工作[25]基于具有良好抗噪性能的零化神经网络[26]、牛顿积分增强型网络[27]、饱和约束神经动力学模型[28]等，汲取这些网络设计中的优势结构，从神经网络求解能力与鲁棒性两个层面入手开发用于k-WTA操作的新型神经网络。

此外，随着计算能力与存储能力的提升，工业控制规模的不断扩大，从分布式的角度处理问题的方法备受关注。迄今为止，包括上述成果在内的k-WTA研究大多以集中式方式实现。换言之，上述工作未考虑任何拓扑约束，无法直接应用于具有任意拓扑结构的连通图。Li 等人[29]首次明确考虑了群体间的交互拓扑结构，并提出了一种分布式WTA模型来解决群体系统中的动态竞争问题。基于这一研究，Zhang等人[30]从QP形式的k-WTA问题入手，直接构建了一种分布式k-WTA模型，具有良好的容错性与全局收敛性。这些成果点明了研究分布式k-WTA网络的必要性，为后续基于k-WTA思想的广泛应用奠定了基础。

本文回顾了k-WTA网络的发展及求解算法的研究现状，并以分布式k-WTA网络的构建为核心，介绍了包含多机器人系统在内的应用前景。

1 问题建模与算法构建

针对理论实现或应用场景中不同的侧重点，k-WTA可被表述为各种不同的形式[31]，进而设计不同方案来求解该操作。本文给出一种典型的数学映射来表示泛化的k-WTA属性：

(1)

式中，u∈m和y∈m分别表征k-WTA系统的输入和输出信息；ui和yi分别为u和y的第i个元素；k表示期望获取的输出信息y最大值的个数。从数学角度而言，k-WTA反映为从数据阵列中选择最大值的操作。文献[18]已经证明式(1)可被重新规划为一个LP问题：

最小化 -uT(t)y(t),

(2)

式中，上标T为转置运算符；q=[1,1,…,1]T∈m。类似地，式(1)可被等价转化为一个QP问题[19]：

(3)

在已有的成果中，若干有效的递归神经网络模型被陆续构建用于解决式(2)或式(3)。例如，Xia等人[32]针对式(2)提出了一种源对偶神经网络：

其中，x∈为放缩参数；Γ1(·)为分段线性激励函数：

Gu等人[18]针对式(2)提出了一种投影神经网络：

其中，x∈；δ>0为放缩参数；ε2为一个正常数；Γ1(·)的定义同前所述。

文献[19]针对式(3)提出了一种简化的对偶神经网络：

y=Γ3(u-qx),

其中，x∈；δ>0为放缩参数；Γ2(·)和Γ3(·)均定义为单调且不连续的激励函数：

然而，上述算法存在两方面的缺陷：一是这些算法面向静态k-WTA而构建，不适用于求解实际动态问题或具有动态特性参数的问题，由于其没有考虑动态参数的导数信息，会带来较大的滞后误差；二是这些模型均未考虑包括截断误差、舍入误差等设备误差，以及环境干扰在内的噪声影响，使得模型的求解精度无法得以保证。考虑到以上算法所面临的挑战，文献[25]提出了一种鲁棒kWNN模型。首先将式(3)所示的QP问题等价转化为非线性方程组D(t)z(t)-ρ(t)=0。该方程具体的参数构成为：

(4)

其中E(t)=[Im×m;-Im×m]；λ(t)∈和η(t)∈2m分别为式(3)中等式和不等式约束对应的Lagrange乘子；

s(t)=[q;0m]为由1和0组成的向量；(t)=s(t)-E(t)y(t)；ι→0+∈2m。进而所构建的kWNN模型被表示为：

(5)

2 分布式通信结构实现

Olfati-Saber等人[34]在一致性算法方面做出了开创性的工作，分析了不同通信拓扑和时延下稳定收敛的一致性问题。之后的工作[35]研究了移动网络的动态平均一致性协议，并构建了比例型及比例积分型一致性滤波器,这为该领域的研究人员提供了开拓性的思路。基于这些工作，Freeman等人[36]设计了一种改进的比例积分算法，在提高收敛速度和稳定性的同时，完全消除了一致性中的稳态误差。此后，相关探索层出不穷，涌现了多方面的成果[37]。此外，状态饱和、输入饱和、输出饱和的一致性问题也成为研究热点。例如，文献[38]研究了输入饱和对一类线性多智能体系统的影响，并在此情况下实现了分布式自触发共识。进一步，考虑实际通信情况，输入饱和与状态饱和两种约束下的一致性被研究[39]，并提供了一致性算法稳定性的充分条件。文献[40]研究了输出饱和的一致性问题，主要考虑了由测量单元的范围限制带来的有界非线性特性。另一个值得回顾的是文献[41]所开展的工作，其研究了包括非理想通信链路的线性协议、具有输入饱和的非线性协议等在内的多种一致性协议。

(6)

为降低通信消耗并保持系统的可扩展性与稳定性，在成本溢出或参与者出现通信中断或阻塞的情况下，需要及时进行拓扑切换。Jin等人[43]在文献[44]的基础上给出了一种基于切换拓扑的一致性滤波器：

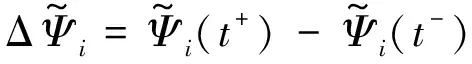
3 基于k-WTA的多机器人竞争协同

多机器人系统因具有良好的容错性、高效性和可扩展性[45]，适用于处理各种复杂和不可预测的任务[46]，如运动规划[47]、搜索和救援行动[48]、自动控制[49]等。受生物/社会群体内部行为机制的启发，多机器人系统的协同行为主要包括合作和竞争两种状态，且二者都具有一定的优势和广泛的应用。例如基于合作行为开展的集群编队、紧急救援等研究[50]，基于竞争行为开展的资源调度、动态围捕等。合作可以使多机器人系统在复杂环境中轻松工作，并提高任务的成功率，而竞争型协同可初步为系统筛选优秀的个体，在节能和降低成本方面有显著的优势。相较于针对多机器人合作展开的研究热潮[51-52]，竞争行为的研究成果较少,其中一个广为人知的方法是强化学习[53-54]。该类方法尤其适用于多机器人系统，这是因为基于强化学习的方法在处理现实环境的不确定性、信息不完全性、分布式学习等问题方面有着突出的优势。然而，它们仍然面临着巨大的挑战。首先，这类方法的实现依赖于大量的数据，带来巨大的计算量以及严重的时间/空间资源消耗，不适合多机器人实际控制场景[55]。其次，虽然这些方法可以在仿真或软件中成功通过测试，但应用于动态且不可预测的真实环境中时，强化学习采用的试错策略[56]会给机器人造成巨大的损失和高昂的成本。再而，针对机器人的强化学习很难设定通用的奖励函数，对于不同的任务场景需要设计不同的函数进而不断训练模型，使得应用强化学习的机器人系统的泛化性大打折扣。鉴于此，从分布式控制的角度实现多机器人协同，可避免上述问题，弱化对环境信息的需求，从而降低多机器人系统的负担,这是值得深入探索与研究的新思路。

3.1 多机器人系统协同方案

现阶段基于k-WTA的多机器人分布式协同相关的研究已取得了若干成果，如文献[25,42,57-58]。具体地，文献[58]面向可被建模为质点的机器人群体，如轮式机器人等，研究了一种分布式竞争模型，其中机器人的运动学和动力学特性可被忽略。具体构建k-WTA指标为:

式中,φi和φt分别代表第i个机器人和目标物的位置。第i个机器人的运动控制动力学被表示为：

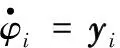
(7)

式中，￡>0是与收敛速度相关的变量，表示连接机器人与目标之间距离与机器人速度变化的反馈增益。显然，输出yi=1所对应的第i个机器人被用于执行追踪任务，而输出yi=0所对应的机器人未激活，静待下一任务目标的来临。

对多机器人系统的研究不应局限于轮式机器人,带有机械臂的机器人已广泛应用于工业制造领域，包括设计、搬运和抓取等场景，尤其在涉及精密任务时，占据着不可取代的地位。例如，航天飞机使用Canadarm来操纵有效载荷。因此，文献[42]将分布式竞争协同行为推广至带机械臂的多机器人系统来完成基于k-WTA的任务分配。考虑一个结构信息均为时变参数的n自由度冗余机械臂，其关节角度为θ(t)=[θ1(t);θ2(t);…;θn(t)]∈n；末端执行器的笛卡尔坐标为r(t)∈p且定义期望轨迹为rd(t)∈p，则运动学方程被表示为Ω(θ(t))=r(t)。其中，Ω(·)代表非线性映射函数，对于确定结构的机器人，其相关参数和设置是已知的。对上式两边求导可得：

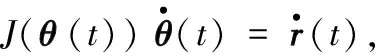
式中，J(θ(t))=∂Ω(θ(t))/∂θ(t)∈p×n为雅可比矩阵；为关节速度向量；为r(t)对时间的导数。注意系数矩阵J在t∈[0,T]的任意时刻都必须是非奇异的，以确保可被求解，其中T为完成期望轨迹的执行时间。因此，假设使用由m个机器人组成的多机器人系统进行协同作业，则需为每个机器人分配期望轨迹，此时每个机器人应满足：

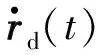
其反映了每个机器人规划的运行路径与期望运动路径之间的距离。继而，在接收到的驱动指令信号的激励下，每个机器人的速度表示为：

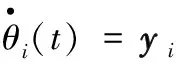
结合实际应用场景，若考虑冗余度机器人的避障能力以及关节速度的安全取值域，则会涉及到对于关节角度、关节角速度、关节角加速度等的约束。这些均可以看作是对于如上驱动指令信号额外考虑饱和约束/映射函数[43]。

3.2 分布式k-WTA协同方案

以式(5)～式(7)为例，构建有限通信环境下用于多机器人竞争协同的分布式k-WTA协同方案为：

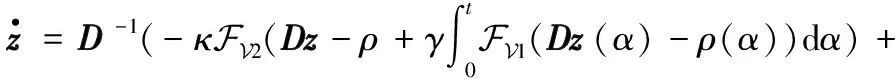
y={z}m,

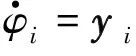
(8)

该系统具体应用步骤如下：

② 初始化相关参数D，ρ(t)和z。

③ 获取φi和φt的信息。

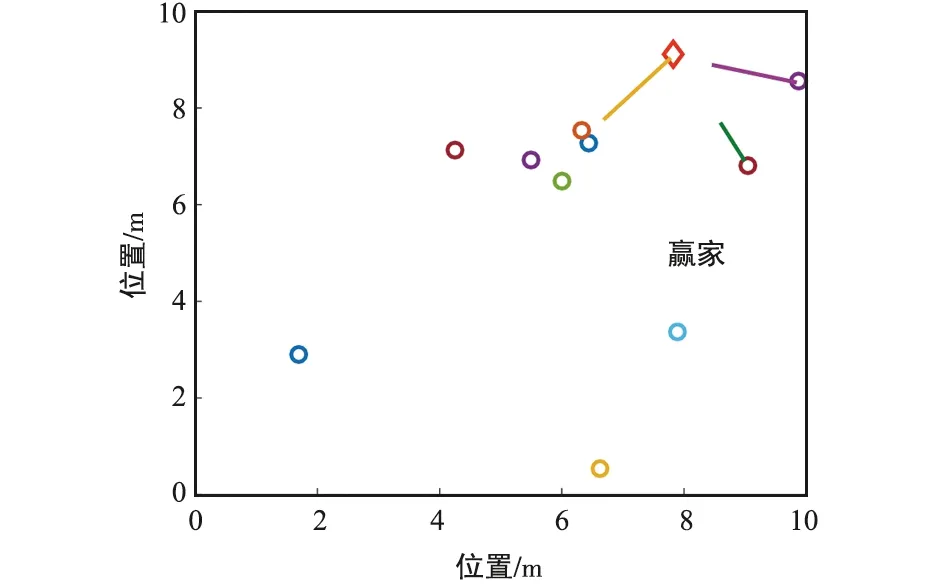
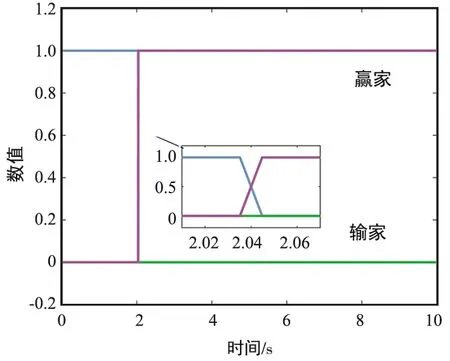
⑥ 判断条件‖yi(φi-φt)‖2

根据分布式k-WTA协同方案(8)及上述实现步骤，可进行相关的仿真验证，结果如图 1～图 6所示。

图1 一个赢家发生替换时，多机器人系统运动轨迹-阶段ⅠFig.1 Motion trajectory of the multi-robot system with a winner replaced-Stage Ⅰ

图2 一个赢家发生替换时，多机器人系统运动轨迹-阶段ⅡFig.2 Motion trajectory of the multi-robot system with a winner replaced-Stage Ⅱ

图3 分布式k-WTA网络的输出Fig.3 Outputs of the distributed k-WTA network

图4 两个赢家发生替换时，多机器人系统运动轨迹-阶段ⅠFig.4 Motion trajectory of the multi-robot system with two winners replaced-Stage Ⅰ

图5 两个赢家发生替换时，多机器人系统运动轨迹-阶段ⅡFig.5 Motion trajectory of the multi-robot system with two winners replaced-Stage Ⅱ

图6 分布式k-WTA网络的输出Fig.6 Outputs of the distributed k-WTA network

4 问题分析与研究展望

考虑到k-WTA思想在社会学以及经济学等多学科领域的研究价值，以及其在包含多机器人系统在内的群体系统协同中的重要理论意义与广阔应用前景，面向k-WTA操作的高性能求解算法开发和分布式网络构建技术仍需不断突破，且基于k-WTA网络的应用场景有待挖掘。例如，如下问题可以作为一些探索的方向：

(1) 开展离散计算模型或算法的研究

一方面，针对k-WTA操作的研究大多基于连续模型。尽管为了在数值设备上实现连续时间模型，已经有各种由数值差分公式导出的数值离散方法。然而，从数据时间定位的角度来看，这些方法大多不适用于处理时变问题，甚至是不可行的。例如，Matlab 中常用求解微分方程的工具“ode15s”，其求解基于龙格库塔方法，但是该方法在使用过程中不仅需要使用当前时刻的信息量，同时需要未来时刻的信息作为输入。然而每一个未来时刻的信息在当前计算时是不可知的，也即此时待求解系统为非因果系统[59-60]。因此，选取一个适合连续时间模型离散化的数值微分公式是得到符合因果律的计算方法的关键。另一方面，实际环境下机器人之间的通信是数字技术驱动的，并未涉及连续时间信号的交换。因此，连续模型对于直接处理信号发送、传输、接收等一系列离散信息操作效率较低。

(2) 开展复杂环境下分布式一致性协议的研究

现有基于k-WTA的竞争工作所考虑的拓扑大多为固定的，导致其在实际环境中的应用受到限制。明确而言，由于整个系统(或参与者)的动态特性和有限的通信范围，通信拓扑通常是需要随时间而变化的。再者，复杂场景中的障碍/干扰或软硬件设备和传感器的任意形式故障等问题可以看作是对系统施加了不可预测的物理约束，这很可能导致通信网络的中断或强制切换[61-62]。当参与者间出现通信中断时，拓扑的不可切换性为系统的平稳运行和应急处理造成了一定的威胁。因此，可变拓扑、切换拓扑，甚至事件触发型拓扑[63]，在分布式一致性协议的研究中都是高效且推荐使用的。此外，实际通信环境中信道增益、时延、非线性等问题为分布式一致性协议的建模、精确性、稳定性提出了更高的要求。

(3) 拓展分布式k-WTA网络的应用

k-WTA思想在众多领域均能够发挥其独特的优势。在深度学习中，k-WTA学习规则作为一种竞争关系的学习规则，可用于无监督学习,具体为通过将网络的某一层确定为竞争层，最终调整该层中响应值最大的神经元(竞争中获胜者)对应的权值。此外，k-WTA学习规则可作为一种典型的聚类算法，通过训练实现聚类中心向样本信息中心的演变,即根据训练对象的特征用于损失函数设计，一定程度上避免梯度平均带来的问题，降低局部最小值的影响。除上述数学或科学领域外，其在社会学问题建模中也占据一席之地，如以意见动力学为代表的社会行为建模。k-WTA思想通常符合包括竞选、竞标、政策、舆论等在内的意见动态演变过程，因此考虑实际信息的不完全共享性利用分布式k-WTA网络进行建模，可以有效预测和评价社会系统演变的趋势。立足现实开放场景，挖掘并研究k-WTA思想及分布式k-WTA网络的应用场景是有潜在价值的。

5 结论

本文对赢者通吃网络的建模、发展及求解算法的构造进行了详细的回顾和讨论。此外，以分布式赢者通吃网络的研究为核心，给出了一种高精度且鲁棒的分布式赢者通吃神经网络算法。进而，以多机器人系统协同为实例，指出了赢者通吃网络的应用前景。这些丰硕的成果极大促进了神经网络理论、分布式网络、机器人技术的发展，并在相关领域取得了极大的进展。最后，分析了现有研究中尚需关注的问题及有待进一步攻关的方向。