太赫兹智能可重构超表面

何贵举，兰 峰,2*，王禄炀，宋天阳，潘一博，陈 智，张雅鑫,2，杨梓强,2

(1.电子科技大学 电子科学与工程学院，四川 成都 611731；2.电子科技大学 长三角研究院(湖州)，浙江 湖州 313001；3.电子科技大学 通信抗干扰技术国家级重点实验室，四川 成都 611731)

0 引言

超表面是物理和信息领域的研究热点之一，但是传统的超表面一旦制备出来，其功能即被固定化，无法根据不同的环境需求实时调控电磁波，以实现不同的功能。从20世纪90年代人工微结构超表面到2010年的编码超表面概念[1]，到2014年崔铁军院士提出信息编码超表面[2]，超表面的形式已由无源被动向智能可控、数字化可编程等主动方式演变，可称之为智能可重构表面(Reconfigurable Intelligent Surface,RIS)。RIS是Massive MIMO的一个演进，只反射或折射入射信号，不需要具备射频链路，避免了硬件复杂度和功耗的问题，可以进一步提升多天线规模，获得更高的波束赋形增益[3-6]。到目前为止，已经出现了大量基于PIN二极管和变容二极管的可重构超表面，编码形式已逐渐从可编程相位扩展到可编程振幅和极化[7-13]。基于前面很多学者的工作基础上，本文研究了一种太赫兹智能可重构超表面，通过对波束的动态调控，可以实现波束扫描、波束卷积和RCS缩减等功能。本研究为RIS的进一步发展奠定了基础，通过构建智能可控无线环境，将有机会增强5G-Advanced网络，并为6G带来一种全新的通信网络范式。

1 超表面单元设计

本文提出的太赫兹智能可重构超表面是基于开关二极管构建的编码阵列，单元结构如图1所示。

图1 单元结构图Fig.1 Unit structure diagram

单元共有4层，分别为金属结构层、第一介质层、金属底板层和第二介质层。金属采用的是电导率为5.96×107的铜，厚度为18 μm，金属结构尺寸为：x1=0.86 mm，x2=0.3 mm，y1=0.39 mm，y2=0.3 mm；第一介质层采用的是介电常数为2.65的F4B，厚度h1=0.55 mm；第二介质层采用的是介电常数为4.3的FR4，厚度h2=0.5 mm；单元周期L=1.5 mm。通过导电柱过孔穿过F4B介质层的过孔与金属底板层连接，接着与FR4介质层连接，在底板层两个导电柱之间有绝缘环来隔离；金属结构层的中心通过打孔与金属底板层和F4B介质基板连接。

通过使用三维电磁场仿真软件(CST)进行单元的频域仿真，设置Floquet端口，边界条件为周期边界。单元的幅值特性如图2(a)所示，当超表面单元上的二极管导通和断开时在频率115～130 GHz幅值基本在-7 dB以上，带宽为15 GHz；单元的相位特性如图2(b)所示，超表面单元上的二极管导通和断开在115～130 GHz 产生了180°左右的相位差。二极管的等效模型如图2(c)所示，二极管型号是MA4AGFCP910。

(a) 单元幅值

(b) 单元相位

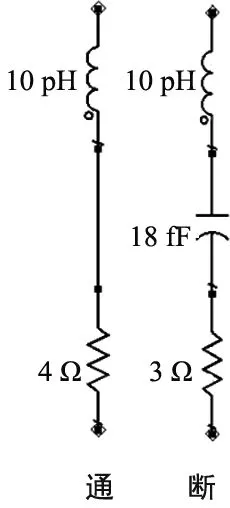
(c) 二极管等效模型

当二极管导通时相当于电阻和电感串联，二极管断开时相当于电阻、电容和电感串联。可重构编码超表面由于其单个超表面单元的状态可以被二进制数字控制，将单元按照特定的顺序排布在二维平面上以获得不同的功能。

2 多功能重构

2.1 波束扫描

根据相移梯度调控实现波束扫描的原理，为了产生不同角度的波束，超表面单元按照不同的X梯度编码序列排布在二维平面上，通过控制单元结构上二极管的通和断，可以控制电磁波相位实现不同角度的反射。超表面编码阵列如图3(a)所示，不同Nx的编码序列如表1所示，按照表1 的编码序列，在CST中排列成32×32的编码阵列。仿真后的二维波束图如图3(b)所示，可以看到随着Nx的增大，波束扫描角度逐渐减小。由于Nx只取整数值，这种粗糙的离散方法使得反射波束的角度无法连续变化，在相邻波束切换的两个角度之间存在一个盲区，即一个无法控制波束向其辐射的区域。本文提出采用分数化编码方法[14]实现在高精度分数化取值下匹配对应的编码序列，Nx以0.5为步长达到对相移梯度的高精细离散，以实现波束的连续性灵活控制。仿真结果证明编码超表面可以实现±24°的波束扫描。

(a) 超表面编码阵列

(b) 二维波束图图3 波束扫描Fig.3 Beam scanning

表1 编码序列

2.2 波束卷积

为了进一步验证超表面单元的多波束重构能力，通过卷积定理[15]将两种不同功能的编码序列叠加实现波束角度的偏移。

卷积定理为：

(1)

将此定理应用到远场散射模式：

E(sinθ-sinθ0)。

(2)

卷积后的远场波束角度计算公式：

(3)

式中，θ1和θ2为梯度编码的反射角，θ为卷积后的反射角。

当Nx=4时，对应的x梯度编码11110000……用Snell公式的验证计算结果为：θ=11.7°，φ=0°，当Ny=8时，对应的y梯度编码111111110000000……用Snell公式的验证计算结果为：θ=5.8°，φ=90°。将上述两种编码进行卷积运算，对应卷积后的编码波束角度用公式(3)计算，结果为：θ=12.6°，φ=26.4°。图4(a)为Nx=4和Ny=8时的二维远场波束图，图4(b)为卷积后的二维远场波束图，仿真与计算结果相符合。

当Ny=16时，对应的y梯度编码为11111111111111110000000000000000，用Snell公式的验证计算结果为：θ=2.9°，φ=90°。将Nx=4与Ny=16两种编码进行卷积运算，对应卷积后的编码波束角度用式(3)计算，结果为：θ=12°，φ=14°。如图4(c)所示，为Nx=4和Ny=16时的二维远场波束图；图4(d)为卷积后的二维远场波束图。从这两种卷积编码可以发现，波束发生偏移并且产生了4个波束，这里只显示了φ面的波束，另外﹣φ面也有2个波束。仿真结果表明通过卷积原理可以实现任意波束的搬移。

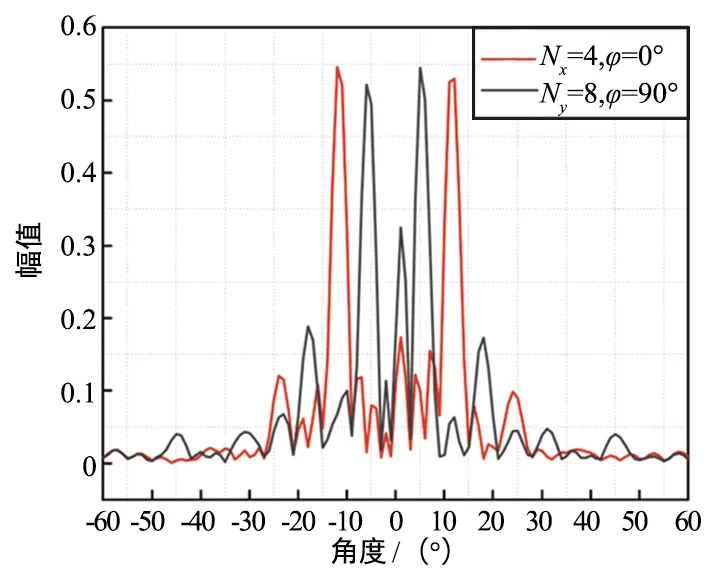
(a) 卷积前波束1

(b) 卷积后波束1

(c) 卷积前波束2

(d) 卷积后波束2

2.3 RCS缩减

雷达散射截面(RCS)是测量目标对特定方向入射电磁波散射功率的物理量。超表面单元对于入射的电磁波没有吸收或者损耗作用，而是将入射电磁能量散射到各个方向，尽可能形成较多的波束。根据能量守恒定理，每个波束的散射能量将会很低，从而实现RCS缩减。根据GRS优化编码[16]，使超表面阵列产生的散射波束在所有可能的方向上均匀分布。与简单的棋盘编码相比，这意味着在单稳态和双稳态的超表面RCS的相当大的减少。通过递推公式：

δ0=1，δ2n=δn，δ2n+1=(-1)nδn。

(4)

得到P型编码：

σn=δn，n=0,1,…,N-1,

(5)

Q型编码：

(6)

令σn=1代表编码1，σn=-1代表编码0。每一个4×4的小阵列为一个超级子单元，代表一位编码0/1。如图5(a)所示，取N=7时的8位P型GRS编码，每个超级子单元代表一位编码0/1组成32×32编码阵列。通过在CST中进行仿真，得到的三维远场方向图如图5(b)所示，可以看到反射波束被散射到了各个方向，但是中间有较强的镜面反射。为了优化编码的空间安排，根据卷积定理对P型编码和棋盘式编码进行卷积，得到了一种新的卷积优化编码，它显著消除了镜面反射，从而提高了散射波的均匀散度。具体的卷积编码方案如图6所示，把卷积后编码排布成阵列结构在CST中进行仿真，仿真的三维远场波束如图7所示，可以看到波束被均匀地分散到各个方向且能量非常低，并且中间的镜面波束被消除，更好地实现了RCS缩减。如图8(a)所示，P型编码阵列、金属板和P+棋盘编码阵列在125 GHz的二维RCS缩减图，可以看到卷积后的P+棋盘编码阵列幅值平均在-10 dB以下，相比较金属板和P型编码，优化后的卷积编码更好地消除了中间的镜面反射，使电磁波均匀地散射到各个方向。 电磁波斜入射15°不同频点的RCS缩减图如图8(b)所示，可以看到编码超表面在斜入射时依然有很好的RCS缩减效果。

(a) P型编码

(b) 三维远场图图5 P型编码阵列和三维远场图Fig.5 P-type coding array and 3D far-field diagram

(a) 编码方案图

(b) 卷积编码方法示意图图6 卷积编码方案图Fig.6 Convolutional coding scheme diagram

图7 P+棋盘编码三维远场图Fig.7 P + checkerboard coding 3D far-field diagram

(a) 不同角度RCS对比

(b) 不同频点RCS对比图8 RCS缩减图对比Fig.8 RCS reduction diagram comparison

3 结论

本文主要研究了一种太赫兹智能可重构超表面，为了验证超表面单元的多功能波束可重构能力，超表面单元根据不同的编码序列进行排列，实现了波束扫描、波束卷积和RCS缩减等功能。仿真结果证明，编码超表面单元可以在太赫兹频段实现±24°的波束扫描；可以把两个不同编码序列进行卷积，实现波束的搬移；通过优化编码序列，可以实现在115～130 GHz斜入射15°电磁波照射下，RCS缩减在15 dB以下。本研究为太赫兹智能编码超表面的发展提供技术基础，在未来6G太赫兹通信领域有重要的应用前景。