冷热电联供系统多时间尺度滚动优化运行方法研究

2022-04-01陶鸿俊

动力工程学报 2022年3期

王智，陶鸿俊，张玲

(华北电力大学能源动力与机械工程学院，河北保定 071003)

冷热电联供(combined cooling, heating and power，CCHP)系统是一种包含发电、供冷、供热和储能等不同能量设备在内的供能模式，可实现冷热电多元化供能，具有能源利用率高、供电可靠性高、环境污染小和调度灵活等特点，已成为分布式供能的主要形式[1]。然而，CCHP系统中不同能量设备之间耦合集成形式复杂多样，并且可再生能源出力及多元用户负荷的多重不确定性，给CCHP系统高效、可靠和稳定运行带来很大挑战。此外，CCHP系统包含能量生产、传递、转换、传输和消费等多种能量设备，不同能量设备的响应时间差异大，给CCHP系统的协调运行带来挑战。因此，需要在CCHP系统运行的高效性和平稳性方面开展深入研究。

目前，在CCHP系统优化设计及运行研究方面，张诗鸣等[2]构建了冷热电联供单元与液化天然气冷能阶梯利用的能源系统，以运行成本最低为目标，建立多源区域型分布式冷热电联供系统的协同优化模型。顾伟等[3]针对热电联供系统的优化运行问题，建立了多目标规划模型，对系统容量进行优化配置，实现CCHP系统的动态调度。徐青山等[4]分析了典型冷热电联供系统的供能结构，建立考虑系统间电能交互的冷热电联供型系统优化经济调度模型。王锐等[5]建立了CCHP系统，并考虑风电、光伏功率以及热电负荷的随机性，采用机会约束规划理论建立经济运行优化模型。Talebjed等[6]将热经济性分析与可靠性评估相结合，设计了一种规划CCHP系统能源集线器的新方法，建立了一种成本效益最佳的CCHP系统，并引入“实际可用性”指标来表示CCHP系统的可用性。Ren等[7]提出了2种集成太阳能和地热能的CCHP系统，构建了混合CCHP系统的多目标数学模型，确定系统的最佳配置。王志光等[8]基于粒子群优化算法，以联供系统经济性、环保性和节能性为优化目标，对以微型燃气轮机(以下简称微燃机)为核心的CCHP系统进行规划和优化设计，优化了微燃机配置，确定了微燃机机组最佳的运行模式。上述研究分别采用不同的优化方法求解CCHP系统的日前调度与模型规划，但是其均是基于历史负荷和可再生能源数据进行优化的，设备的出力均基于长时间尺度负荷，并没有考虑负荷和可再生能源出力的时变特性。

为了减小功率波动和源-荷偏差对实际系统运行的不利影响，现阶段许多学者建立了多时间尺度的优化模型。汤翔鹰等[9]提出了多时间尺度优化调度策略，以减少可再生能源出力和负荷需求的不确定性对系统的影响。吴鸣等[10]提出了基于模型预测控制的CCHP系统动态优化调度策略，来应对可再生能源的大规模接入及负荷的不确定性。Gu等[11]提出了一种包含反馈机制的模型预测控制方案的在线优化方法。何畅等[12]考虑源-荷不确定性及储能设备配置对CCHP系统优化调度的影响，提出基于多时间尺度和多元储能的综合能源系统优化调度策略。王成山等[13]建立了包含滚动优化环节和动态调整环节的两阶段多时间尺度模型预测控制调度策略。靳小龙等[14]针对含智能楼宇的CCHP系统，提出一种基于模型预测的多时间尺度调度方法。张海涛等[15]建立了包含日前经济优化调度和日内调度2个阶段的多时间尺度微电网能量管理优化调度方案。上述研究在日内优化过程中没有考虑CCHP系统内设备功率调整量对运行的影响。

基于此，笔者以CCHP系统为研究目标进行日前、日内优化，并在日内调度过程中，采用多时间尺度滚动优化方法，提出了CCHP系统优化调度策略；建立了日前经济优化调度和日内滚动优化调度模型，在日前调度阶段确定了最佳系统结构；在日内滚动优化中确定最佳控制时域长度，引入功率调整量惩罚项，实现源-荷间多种能量的协调优化调度；同时将日内滚动优化的运行成本与系统理想成本进行对比，验证日内滚动优化在优化运行成本方面的准确性。

1 CCHP系统结构及热力学模型

CCHP系统的结构如图1所示，主要包括光伏发电设备、微燃机、余热锅炉、换热器、吸收式制冷机、电制冷机、燃气锅炉、蓄电池和蓄热罐，系统同时也与外部电网有电功率交互。系统中的热负荷主要由微燃机和燃气锅炉供给，冷负荷由吸收式制冷机和电制冷机供给，电负荷主要由微燃机、光伏系统和外部电网供给。

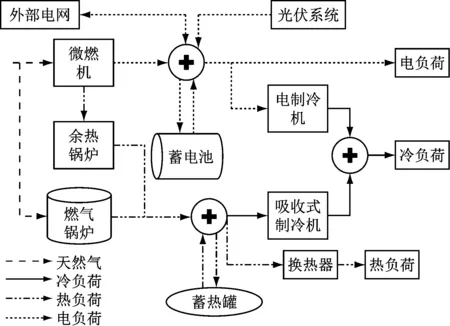
图1 CCHP系统结构图Fig.1 CCHP system structure diagram

1.1 微燃机模型

微燃机是CCHP系统的核心设备，微燃机的燃料消耗功率可表示为：

(1)

式中：Pmt,t为t时段微燃机发电功率，kW；Fmt,t为t时段微燃机耗气功率，kW；ηmt,t为t时段微燃机发电效率，取0.3。

微燃机运行功率约束和爬坡功率约束如下：

Umt,tPmt,min≤Pmt,t≤Umt,tPmt,max

(2)

Umt,tPmt,down≤Pmt,t-Pmt,t-1≤Umt,tPmt,up

(3)

式中：Pmt,min、Pmt,max分别为微燃机的最小出力功率和最大出力功率,kW；Pmt,up、Pmt,down分别为微燃机输出电功率爬坡速率的上限和下限，kW；Umt,t为t时段微燃机的启停状态标记位，取0和1变量，1为工作，0为不工作。

1.2 余热锅炉

余热锅炉通过回收微燃机所产生的废热，达到对废热的进一步利用，以减少能量的浪费。

(4)

式中：Pre,t为t时段微燃机的排气回收余热功率，kW；ηloss为散热损失效率，取0.2；ηhr为烟气热回收效率，取0.8。

1.3 光伏发电系统

光伏系统输出功率PPV,t与太阳辐射强度和环境温度有关，模型[16]如下：

(5)

光伏电池表面温度Tcell,t的计算公式[17]为：

(6)

式中：PPV,t为t时段光伏系统输出功率，kW；PSTC为光伏系统额定功率，kW；fPV为光伏功率降额因子，取0.9；It为t时段实际太阳辐射强度，W/m2；ISTC为标准测试条件下太阳辐射强度，取1 000 W/m2；TSTC为标准测试条件下环境温度，取25 ℃；Tamb,t为t时段实际环境温度，℃；k为光伏功温系数，取-0.47%/K；TNOCT为额定电池工作温度，取47 ℃。

1.4 电制冷机和吸收式制冷机模型

电制冷机利用电能通过压缩机制冷，其输出冷功率Cec,t与输入电功率Pec,t的关系为：

Cec,t=Pec,tCCOP,ec

(7)

式中：CCOP,ec为电制冷系数，取4.0。

吸收式制冷机利用低品位热能转化为冷能，其输出冷功率Cac,t与输入热功率Pac,t的关系为：

Cac,t=Pac,tCCOP,ac

(8)

式中：CCOP,ac为吸收式制冷机制冷系数，取0.7。

1.5 燃气锅炉

燃气锅炉在供热不足时作为补充热源，其输出热功率Pb,t与消耗天然气功率Fb,t的关系如下：

Pb,t=ηbFb,t

(9)

式中：ηb为燃气锅炉的热效率，取0.85。

1.6 蓄电池

蓄电池储能状态方程为：

Wbt,t+1=Wbt,t·(1-σbt)+

(10)

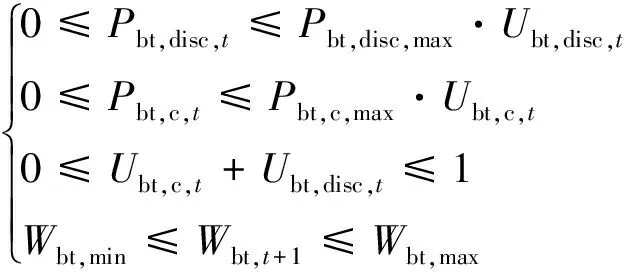
(11)

蓄电池充放电爬坡功率约束条件如下：

Pbt,c,down≤Pbt,c,t+1-Pbt,c,t≤Pbt,c,up

(12)

Pbt,disc,down≤Pbt,disc,t+1-Pbt,disc,t≤Pbt,disc,up

(13)

式中：Pbt,c,t和Pbt,disc,t分别为t时段电池充、放电功率，kW；Δt为时段长度；Pbt,disc,max和Pbt,c,max分别为蓄电池的最大放电功率和最大充电功率,kW；Wbt,t和Wbt,t+1分别为t时段和t+1时段蓄电池存储的电能，kW·h；Wbt,min和Wbt,max分别为蓄电池内储存电能的最小值和最大值，kW·h;σbt为电池自放电率，取0.001；ηbt,c和ηbt,disc分别为蓄电池的充电效率和放电效率，取0.95；Ubt,c,t、Ubt,disc,t分别为t时段蓄电池充、放电状态标记位;Pbt,c,up、Pbt,c,down和Pbt,disc,up、Pbt,disc,down分别为电池充电爬坡功率的上、下限和放电爬坡功率的上、下限，kW。

1.7 蓄热罐

蓄热罐储能状态方程为：

Qtst,t+1=Qtst,t·(1-σtst)+

(14)

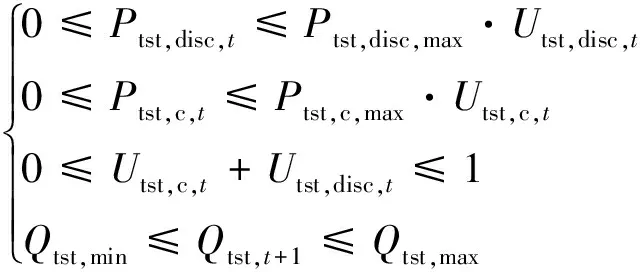
(15)

式中：Ptst,c,t和Ptst,disc,t分别为t时段蓄热罐储热功率和放热功率，kW；Qtst,t和Qtst,t+1分别为t时段和t+1时段蓄热罐存储的热能，kW·h；σtst为蓄热罐自耗热率，取0.005；ηtst,c和ηtst,disc分别为蓄热罐的储热效率和放热效率，均取0.9；Ptst,disc,max和Ptst,c,max分别为蓄热罐的最大放热功率和最大储热功率，kW;Qtst,min和Qtst,max分别为蓄热罐内储存热量的最小值和最大值，kW·h;Utst,c,t和Utst,disc,t分别为t时段蓄热罐储、放热状态标记位。

1.8 与外部电网交互功率

与外部电网交互功率应满足上下限约束：

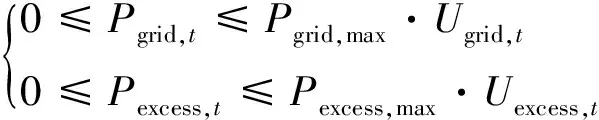
(16)

式中：Pgrid,t和Pexcess,t分别为t时段系统向电网购电和售电功率，kW；Pgrid,max和Pexcess,max分别为系统的最大购电功率和最大售电功率，kW;Ugrid,t、Uexcess,t分别为t时段系统从电网买电、售电功率的状态标记位。

同一时段内，不能同时进行购电和售电，满足状态互斥。

0≤Ugrid,t+Uexcess,t≤1

(17)

2 基于多时间尺度滚动优化调度策略

2.1 优化过程

基于日前预测的可再生能源出力和各类负荷需求，考虑分时电价和各类设备运行约束，时间分辨率为1 h，以一天内CCHP系统的日运行成本最低为目标，确定全天的最优调度计划值。

在日前预测的基础上，日内预测控制调度以可再生能源及用户的冷热电需求的短期预测值为基础，并以日前优化调度值为参考，以15 min为时间尺度[10]，进行日内滚动优化，实现多种源-荷之间的最佳能量匹配。

日前和日内滚动优化调度关系以及多时间尺度策略实施流程如图2和图3所示。

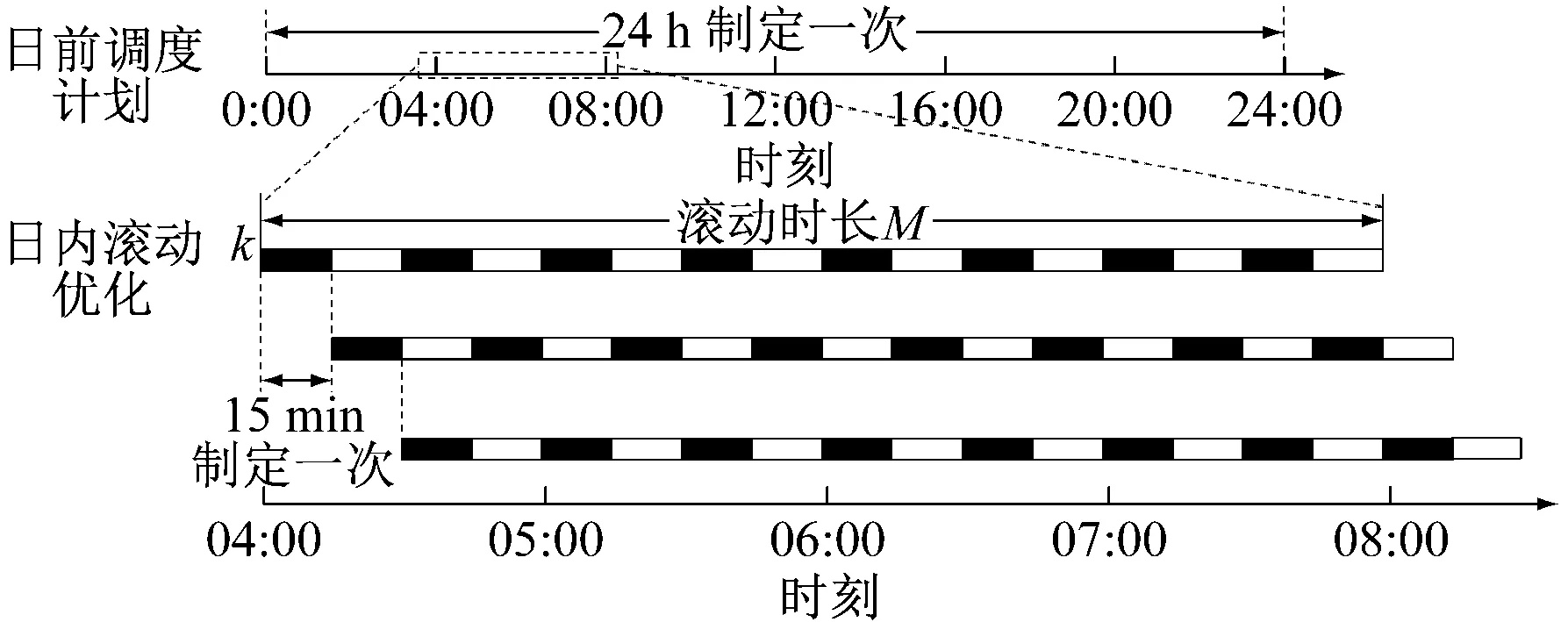
图2 日前和日内滚动优化调度关系Fig.2 The relationship between day ahead and intraday rolling optimization scheduling

2.2 日前优化

日前调度优化目标为：

(18)

式中：T为日前调度周期，为24 h;Cgrid,t为t时段CCHP系统与电网交互费用，元；Cng,t为t时段天然气费用，元；Cbt,t为t时段蓄电池老化成本，元；Com,t为t时段系统运行维护成本，元；Cen,t为t时段系统环境费用，元；CDh为系统日运行成本，元。

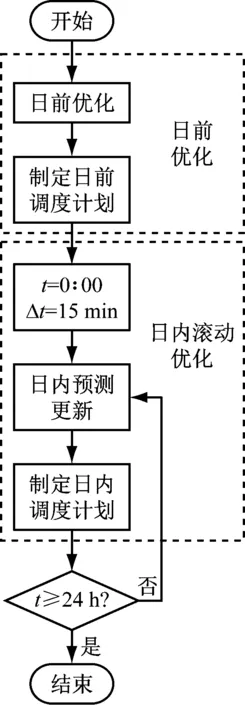
图3 多时间尺度策略实施流程Fig.3 Multi-time scale strategy implementation process

(1) 电网交互费用

Cgrid,t=(Rgrid,tPgrid,t-Rexcess,tPexcess,t)·Δt

(19)

式中：Rgrid,t为t时段对应的购电价格，元/(kW·h)；Rexcess,t为t时段对应的售电价格，元/(kW·h)。

(2) 天然气费用

(20)

式中：Rng为天然气价格，取3.24元/m3；Hng为天然气低位热值，取9.78 (kW·h)/m3。

(3) 蓄电池老化成本[18]

Cbt,t=πbt(Ubt,disc*,t+Ubt,c*,t)·Δt

(21)

式中：πbt为电池单位时间老化成本，18元/次；Ubt,c*,t和Ubt,disc*,t分别为t时段蓄电池开始充、放电标记位。

(4) 运行维护成本

Com,t=[Pmt,t·Kom,mt+Pb,t·Kom,b+Lh,t/ηhe·

Kom,he+Pac,t·Kom,ac+Pec,t·Kom,ec+PPV,t·

Kom,PV+Pre,t·Kom,hr+(Pbt,c,t+Pbt,disc,t)·

Kom,bt+(Ptst,c,t+Ptst,disc,t)·Kom,tst]·Δt

(22)

式中：Kom,mt为微燃机单位运行维护成本，元/(kW·h)；Kom,b为燃气锅炉单位运行维护成本，元/(kW·h)；Kom,he为换热器单位运行维护成本，元/(kW·h)；Kom,ac为吸收式制冷机单位运行维护成本，元/(kW·h)；Kom,ec为电制冷机单位运行维护成本，元/(kW·h)；Kom,PV为光伏系统单位运行维护成本，元/(kW·h)；Kom,hr为余热锅炉单位运行维护成本，元/(kW·h)；Kom,bt为蓄电池单位运行维护成本，元/(kW·h)；Kom,tst为蓄热罐单位运行维护成本，元/(kW·h)；Lh,t为用户热负荷，kW；ηhe为换热器效率，取0.8。

(5) 环境费用

Cen,t=[Pgrid,t·Egrid,CO2+(Fmt,t+Fb,t)·Eng,CO2]·

βCO2·Δt+[Pgrid,t·Egrid,SO2+(Fmt,t+Fb,t)·

Eng,SO2]·βSO2·Δt+[Pgrid,t·Egrid,NOx+

(Fmt,t+Fb,t)·Eng,NOx]·βNOx·Δt

(23)

式中：Egrid,CO2、Egrid,SO2和Egrid,NOx分别为从电网购电所产生的CO2、SO2和NOx的排放量，g/(kW·h)；Eng,CO2、Eng,SO2和Eng,NOx分别为天然气燃烧所产生的CO2、SO2和NOx的排放量，g/(kW·h)；βCO2、βSO2和βNOx分别为CO2、SO2和NOx的污染物处理成本，元/g。

运行约束条件如下：

(1) 冷功率平衡约束

Pac,t·CCOP,ac+Pec,t·CCOP,ec=Lc,t

(24)

式中：Lc,t为系统在t时段的冷负荷，kW。

(2) 热量平衡约束

Pac,t+Lh,t/ηhe+Ptst,c,t=Pmt,t/ηmt,t·

(1-ηmt,t-ηloss)·ηhr+Pb,t+Ptst,disc,t

(25)

(3) 电功率平衡约束

PPV,t+Pmt,t+Pgrid,t+Pbt,disc,t=

Le,t+Pec,t+Pbt,c,t+Pexcess,t

(26)

式中：Le,t为t时段的电负荷，kW。

(4) 蓄电池充、放电状态转换标记约束

Ubt,c,t+1-Ubt,c,t≤Ubt,c*,t

(27)

Ubt,disc,t+1-Ubt,disc,t≤Ubt,disc*,t

(28)

式中:Ubt,c*,t和Ubt,disc*,t分别为t时段蓄电池开始充、放电标记位。

通过对日前长时间尺度优化调度模型进行求解，得到各联供设备运行出力和蓄电池充、放电状态计划值。

2.3 日内滚动优化

遵循CCHP系统的日前运行计划，建立如下目标函数：

minCRoll=Cgrid,r,t+Cng,r,t+Cbt,r,t+Ctst,r,t

(29)

Cgrid,r,t={Rgrid,t(PDh,grid,t+ΔPgrid,t)-

Rexcess,t(PDh,excess,t+ΔPexcess,t)+

μgrid[(ΔPgrid,t)2+(ΔPexcess,t)2]}Δt

(30)

(31)

Cbt,r,t=μbt[(ΔPbt,c,t)2+(ΔPbt,disc,t)2]Δt

(32)

Ctst,r,t=μtst[(ΔPtst,c,t)2+(ΔPtst,disc,t)2]Δt

(33)

式中：CRoll为每次进行滚动优化时控制时域内的运行成本，元；Cgrid,r,t为与电网交互总成本，元；Cng,r,t为燃料成本，元；Cbt,r,t为蓄电池充放、电功率变化惩罚成本，元；Ctst,r,t为蓄热罐储放热功率变化惩罚成本，元；PDh,grid,t和ΔPgrid,t分别为日前购电功率和日内购电调整功率，kW；PDh,excess,t和ΔPexcess,t分别为日前售电功率和日内售电调整功率，kW；μgrid为电网交互功率变化惩罚系数；ΔPmt,t和ΔPb,t分别为日内微燃机和燃气锅炉出力调整量，kW；FDh,mt,t和FDh,b,t分别为微燃机和燃气锅炉日前耗气功率，kW；ΔFmt,t和ΔFb,t分别为微燃机日内耗气功率调整量，kW；μmt和μb分别为微燃机和燃气锅炉出力功率变化惩罚系数;ΔPbt,c,t和ΔPbt,disc,t分别为日内蓄电池充电功率和放电功率调整量，kW；μbt为蓄电池充放电功率变化惩罚系数;ΔPtst,c,t和ΔPtst,disc,t分别为日内蓄热罐储热和放热功率调整量，kW；μtst为蓄热罐储放热功率变化惩罚系数。

滚动优化不仅要满足功率平衡约束和设备约束，还要遵循日前计划的设备运行状态约束。

3 参数设置

系统模型参数设置见表1，电价信息见表2。

过渡季典型日光伏出力和日前负荷预测信息见图4。

4 算例分析

研究位于北京地区的某近零能耗办公楼宇，对该办公楼的CCHP系统进行分析，该办公楼共有12层，每层楼高4 m，总建筑面积6 912 m2。图4给出了过渡季典型日可再生能源出力以及各类负荷的日前数据信息。采用MATLAB、Gurobi优化求解器进行优化求解。

4.1 不同结构对日运行成本的影响

分析了不同结构对CCHP系统运行经济性的影响，具体结构分为：(1) 系统中只设有储热装置(CCHP-T)；(2) 系统中只设有储电装置(CCHP-E)；(3) 多元储能(CCHP-TE),即在系统中配置储热和储电装置。根据式(18)计算过渡季典型日在不同储能模式下的日前运行成本，不同结构的日运行费用见表3。其中，环境费用为消耗天然气和从电网购电所产生的CO2、SO2和NOx污染物的处理费用之和。

表1 系统模型参数

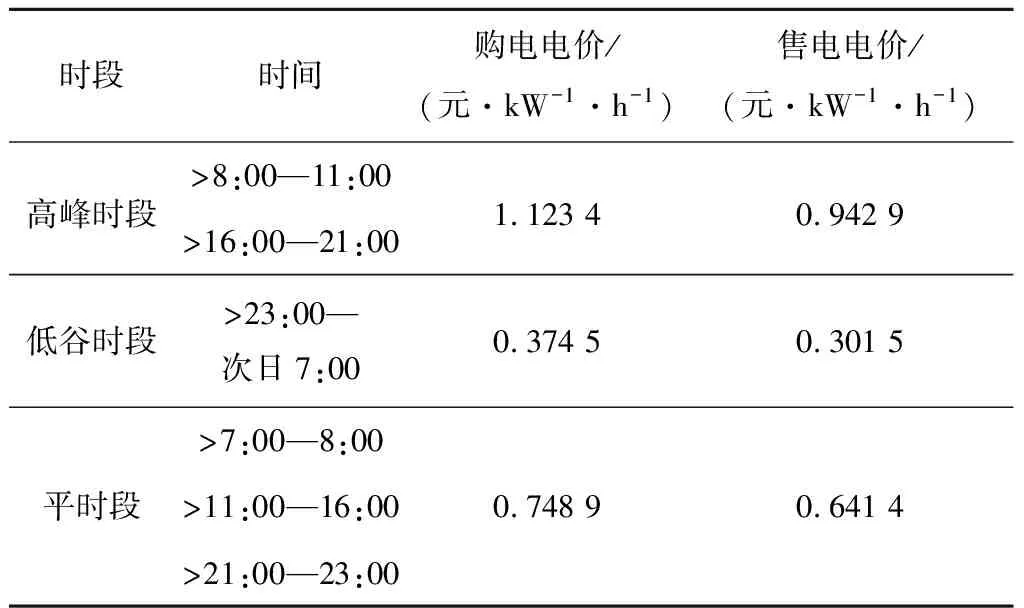
表2 分时电价信息

从表3可以看出，CCHP-TE的日运行成本最低，为545.4元。CCHP-TE的环境费用和日运行成本最低，这是由于蓄热罐和蓄电池的出力减少了电能和天然气的消耗，进而降低了环境费用和日运行成本。运行结果表明，在CCHP-TE结构下，各储能设备协同工作，能够显著降低日运行成本，提高CCHP系统的运行经济性，同时能够保证系统安全平稳运行，故采用多元储能模式来提高系统运行的经济性。

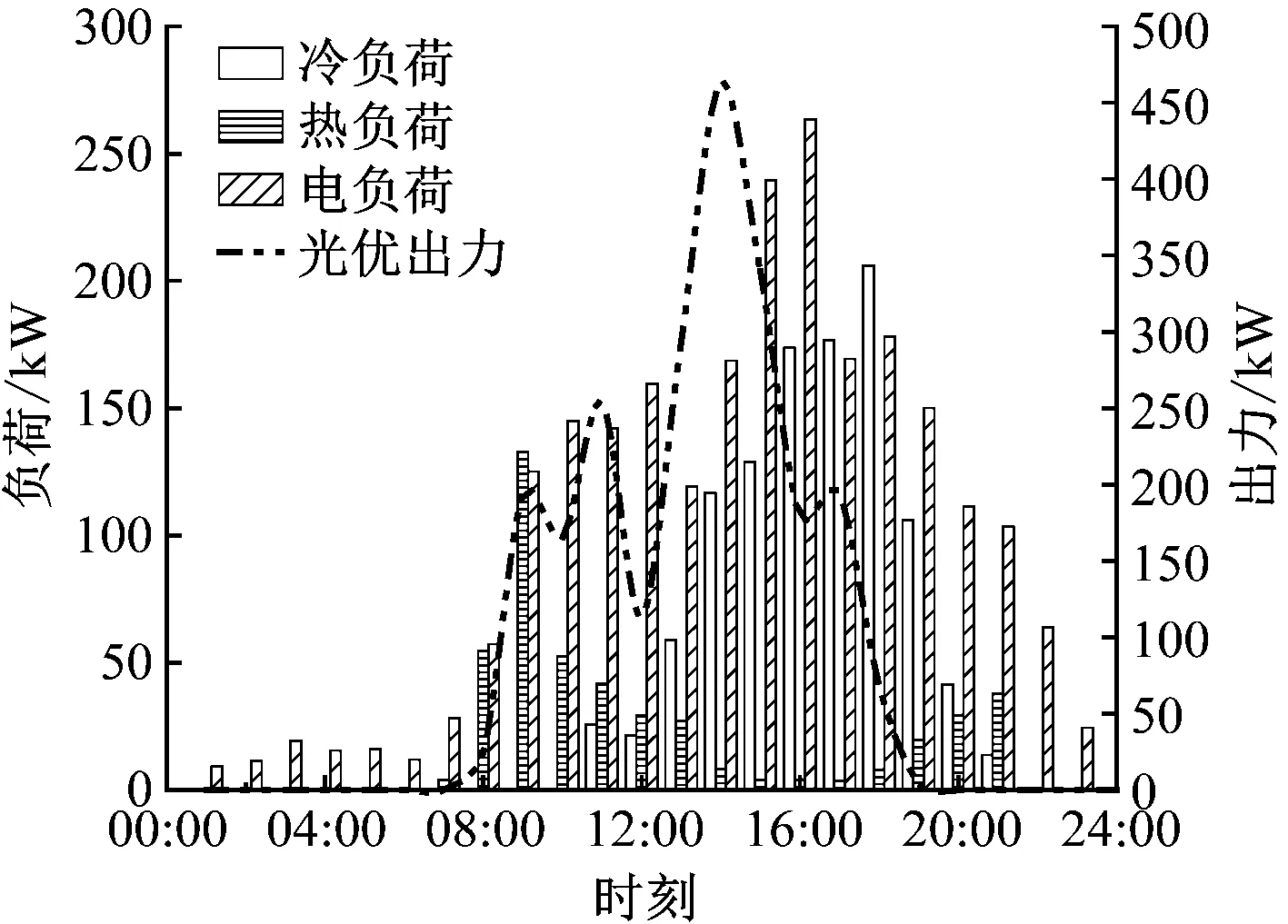
图4 光伏出力和日前负荷预测Fig.4 Photovoltaic output and day-ahead load forecast

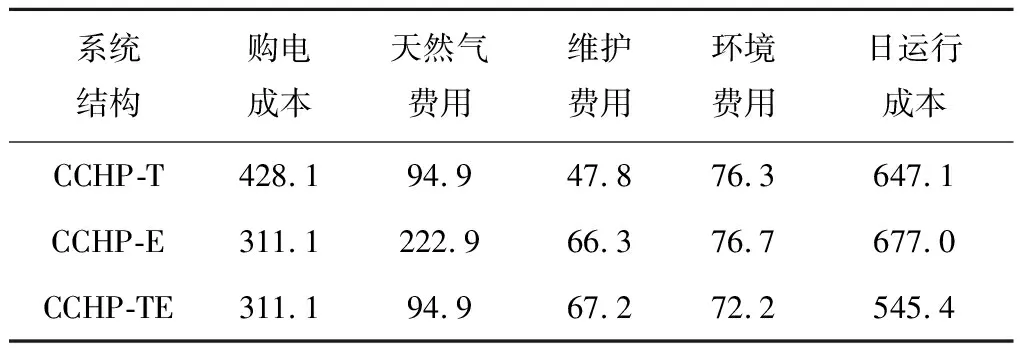
表3 不同结构的日运行费用Tab.3 Daily operating costs of different structures 元

4.2 CCHP-TE系统日前调度结果分析

过渡季典型日的日前调度结果如图5所示，根据日前调度结果可知，微型燃气轮机全天处于停机状态；热负荷先由蓄热罐供给，不足的部分由燃气锅炉供给；冷负荷全部由电制冷机供给；电负荷由外部电网、蓄电池和光伏供给。在>23：00—次日7：00为低谷电价时段，电负荷需求量较低，电负荷全部由外部电网供给并且从电网购电为蓄电池进行充电。在平电价时段，>7：00—8：00和>11：00—16：00的电负荷先由光伏系统供给，光伏系统产生的多余电量进行并网售电，不足的部分由外部电网进行补充；在>21：00—23：00电负荷先由蓄电池进行补充，不足的部分由外部电网供给。在高峰电价时段，>8：00—11：00的电负荷全部由光伏系统满足，光伏系统多余的发电量进行并网出售；>16：00—21：00的电负荷先由光伏系统供给，不足的部分由蓄电池供给，其余的电量缺额由外部电网供给。

冬季典型日的日前调度结果如图6所示，在谷电价时段，微型燃气轮机在01：00—5：00处于停机状态，电负荷全部由外部电网供给，并从电网买电为蓄电池充电；谷电价的其余时段电负荷全部由微型燃气轮机供给，多余的电能为蓄电池充电和并网售出。在平电价时段，>7：00—8：00的电负荷全部由微型燃气轮机满足，多余电量上网；在>11：00—16：00内电负荷先由光伏系统和微型燃气轮机供给，不足的部分由外部电网满足；在峰电价时段内，在>8：00—11：00和>16：00—17：00微燃机处于满负荷运行状态，电负荷先由微型燃气轮机、蓄电池和光伏系统满足，不足的部分由外部电网供给；在>17：00—21：00电负荷由微燃机和蓄电池提供，多余的电量并网售出。

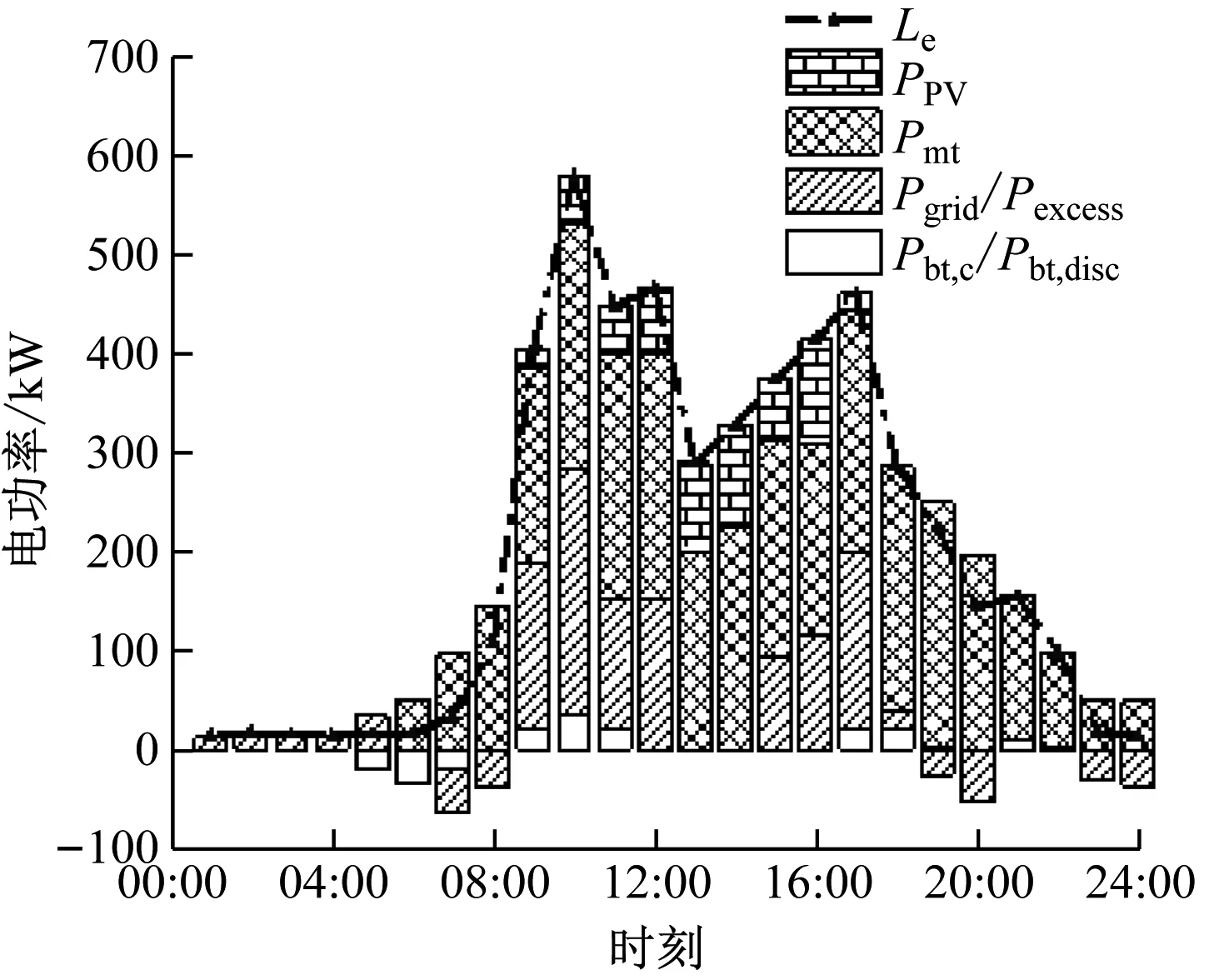
(a) 电能调度

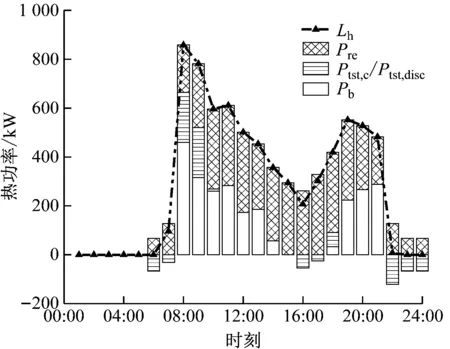
(b) 热能调度图6 冬季典型日日前调度结果Fig.6 Day-ahead scheduling results in the typical day of winter

而在冬季典型日无冷负荷，热负荷先由微型燃气轮机回收余热供给，若有剩余，多余的热量储存到蓄热罐中；不足的部分先由蓄热罐放热补充，若仍有缺额，缺额由燃气锅炉供给。

4.3 日内滚动优化时长的选取

通过计算过渡季典型日的不同滚动优化时长下系统的运行成本，确定最佳的滚动优化时长M。图7为不同滚动优化时长下系统的运行成本。

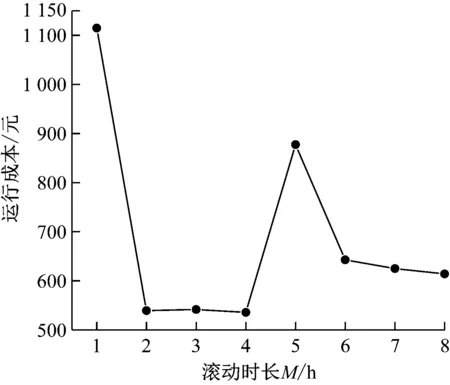
图7 不同滚动优化时长对运行成本的影响Fig.7 Impact of different rolling optimization period on operating cost

由图7可以看出，滚动优化时长从1 h增加到4 h时，运行成本从1 114.7元降低到535.6元。滚动优化时长从5 h增加到8 h时，运行成本从877.5元继续降低到614元，系统运行成本均高于滚动优化时长为4 h所对应的运行成本，同时随着滚动优化时长的增加，计算时间显著增加，根据上述优化运行结果可知，当滚动优化时长取4 h时，系统运行的经济鲁棒性较好，故选定滚动优化时长为4 h，取16个采样点进行滚动优化。

4.4 优化结果分析

为进一步体现日内滚动优化的特点，将多时间尺度协调度与常用的DA-P(Day-ahade programming)的调度结果进行对比分析。DA-P策略是基于日前调度运行基础上，在日内实际系统运行时，预测所带来的电负荷功率波动由外部电网进行供给，热负荷波动由燃气锅炉供给，冷负荷功率波动由电制冷机供给。表4为不同运行策略下CCHP系统在过渡季典型日的运行结果。

表4 不同策略下CCHP系统的运行结果

由表4可知，采用多时间尺度滚动优化能够有效降低运行成本，在DA-P策略下系统日运行成本较日前运行成本上升了10.34%，电网联络线交互功率波动率增加了10.16%；多时间尺度调度策略成本比日前运行成本降低1.80%，电网联络线交互功率波动率只增加了0.89%。由于DA-P调度策略是基于日前的一次离线长时间尺度优化，源荷之间存在较大的误差，在实际运行时仅通过外部网络来平抑预测误差，平抑过程中所产生的购能成本使实际运行成本比日前优化成本上升；而多时间尺度滚动优化在日前计划引导下，在日内优化过程中反复滚动减小偏差，有效地降低了电网联络线交互功率波动率，保证了CCHP系统经济平稳运行。

设备的日前调度和多时间尺度滚动优化的调度结果如图8所示。

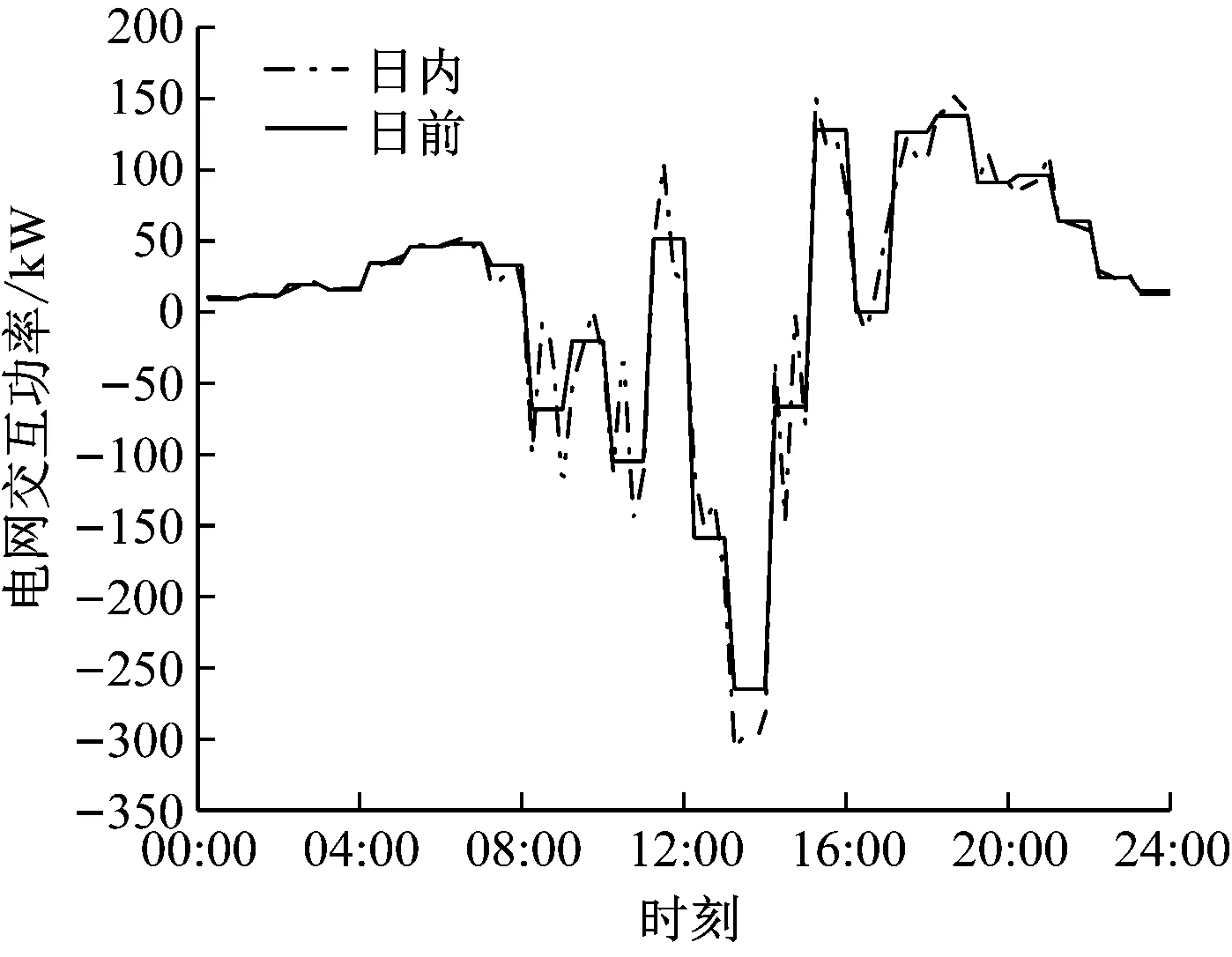
(a) 电网交互功率

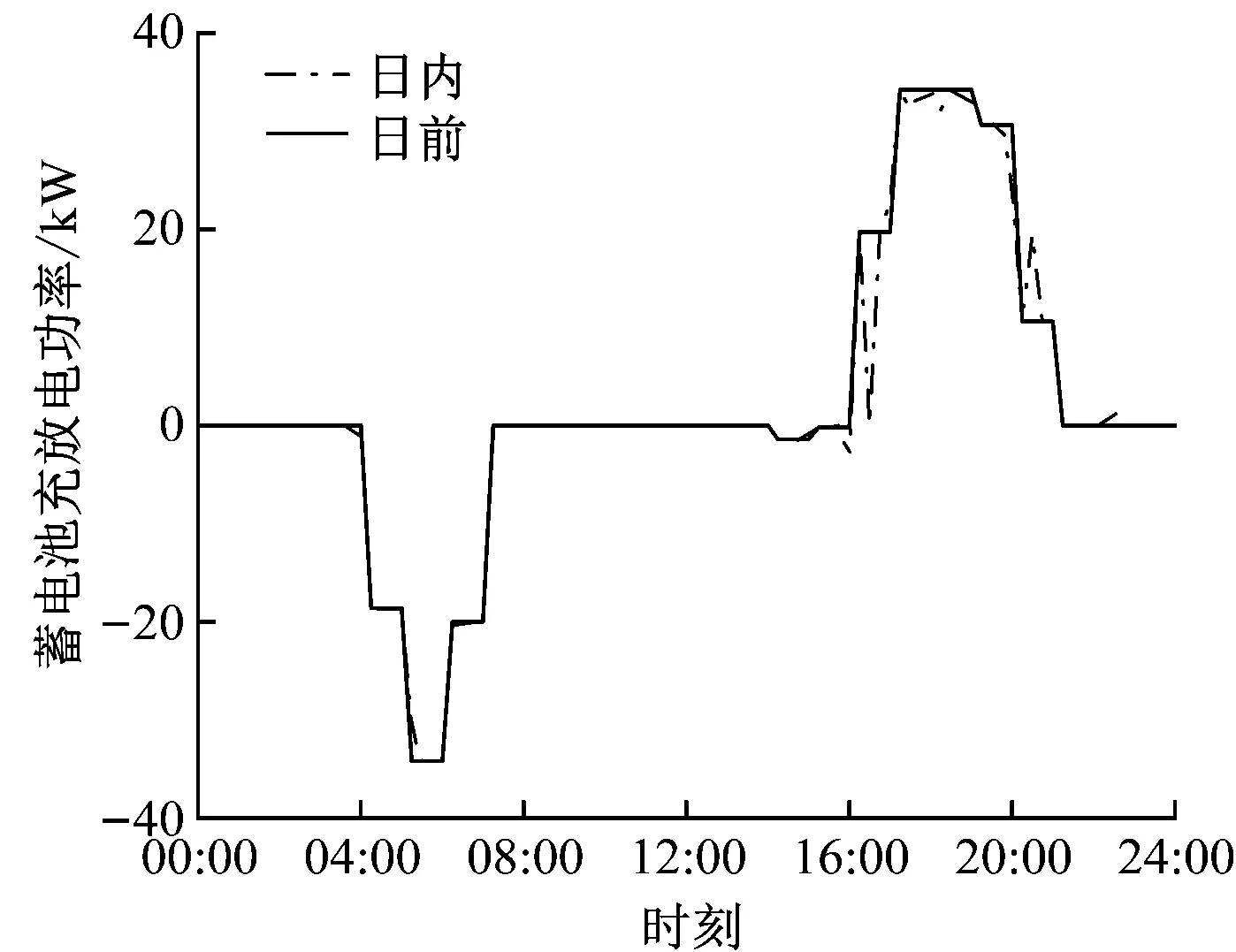
(b) 蓄电池充放电功率图8 日前优化和日内滚动优化的结果Fig.8 Results of day-ahead optimization and intraday rolling optimization

日内滚动优化结果表明，在峰电价时段售电量增加，结合蓄电池调度结果，在谷电价时段购电为蓄电池充电，在峰电价时段蓄电池放电。蓄电池充放电状态保持日前运行计划，避免频繁充放电，可延长蓄电池使用寿命，保证系统经济平稳运行。

不同典型日的日前运行成本和日内滚动优化运行成本如表5所示。由表5可知，日内滚动优化能够有效降低预测误差对调度策略经济性的影响，减小运行偏差。

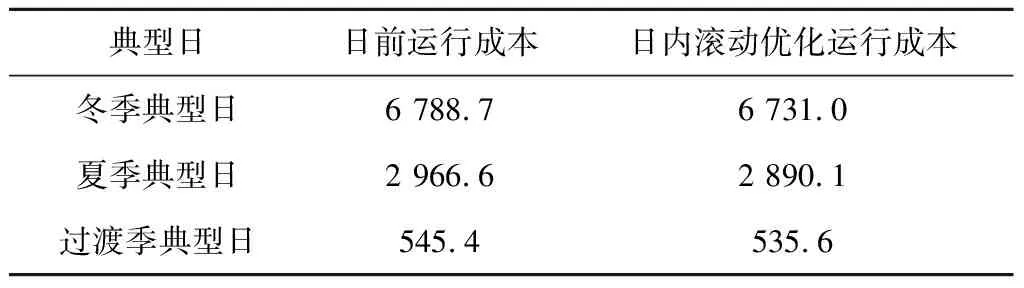
表5 不同典型日的日前运行成本和日内滚动优化运行成本

4.5 理想成本与日内滚动优化成本

假设可再生能源出力和负荷预测是准确的，进行一次全局优化得到的成本为理想成本。理想成本基于准确的负荷和可再生能源出力预测，以15 min为时间尺度有效减小了预测偏差，对未来24 h(96个时段)的运行工况进行统筹考虑和全局优化，得到全面的优化结果，能在更广泛的时间范围内实现优化配置，降低运行成本。优化结果如图9所示。

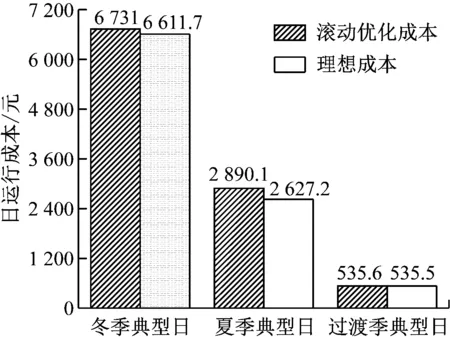
图9 理想成本与日内滚动优化成本对比图Fig.9 Comparison of ideal cost and intraday rolling optimization cost

不同典型日的滚动优化成本均稍高于理想成本，冬季典型日、夏季典型日、过渡季典型日的滚动优化成本分别比理想成本高1.80%、 10.00%和 0.02%。滚动优化算法的成本与理想成本接近，误差较小，能有效体现经济调度的准确性。

不同典型日的日运行成本差异是由不同典型日内的各类负荷需求不同造成的，由负荷预测数据和运行结果可知，在冬季典型日，光伏出力较低，总发电量为550.6 kW·h，系统总热负荷为5 668.3 kW·h，无冷负荷，总电负荷为4 916.9 kW·h，总负荷需求最大。微型燃气轮机和燃气锅炉需要消耗大量天然气和购电来满足热负荷和电负荷需求，因而产生大量的运行费用和环境费用，总运行成本最高；过渡季典型日的冷、热负荷同时存在，但是二者需求量均较低，系统总冷负荷为1 066 kW·h，且冷负荷全部由电制冷机供给，总热负荷为465.1 kW·h，总电负荷为2 324.9 kW·h，且光伏出力较高，光伏总发电量为2 292.5 kW·h，总负荷最低，总运行费用最低。夏季典型日，光伏出力充足，光伏总发电量为2 484.7 kW·h，总冷负荷为6 706.9 kW·h，冷负荷主要由电制冷机供给，无热负荷，总电负荷为3 386.8 kW·h，总负荷介于冬季典型日和过渡季典型日之间，运行费用介于上述二者之间。