不平衡导致的发电机组转子反向涡动分析
2022-04-01何国安阚选恩姜广政常东锋
赵 博, 何国安, 阚选恩, 姜广政, 常东锋
(1. 西安热工研究院有限公司, 西安 710054; 2. 西安西热节能技术有限公司, 西安 710054; 3. 西安理工大学 机械与精密仪器工程学院, 西安 710048)
大型汽轮发电机组是电力系统的核心设备,其发生振动故障会影响设备的安全稳定运行,造成严重的经济损失,甚至发生灾难性事故。基于振动数据分析的轴系故障诊断可以在故障发生早期确定其原因,进而根据诊断结果及时采取措施保障机组长期安全运行[1]。因此,针对大型汽轮发电机组轴系的动力学行为研究具有重要意义。
转子进动方向是振动故障诊断和治理的重要依据特征之一[2-3]。为了准确建立转子反向涡动行为与故障之间的映射关系,研究人员对转子反向涡动机理开展了大量研究。动静碰摩[4-5]、轴颈呼吸裂纹[6]、转子刚度不对称[7-8]和轴承非线性[9]等均会导致转子发生具有相应特征的反向涡动。质量不平衡是旋转机械最常见的振动故障来源,据统计,旋转机械70%以上的振动故障与质量不平衡有关[10]。传统理论认为,不平衡激振力作用下,仅在支撑刚度非对称导致的临界转速分离区域内转子才会发生反向涡动[11]。Muszynska[12]对悬臂外伸端转子进行振动试验发现,轴承刚度为非对称且弯曲和不平衡同时存在时,转子反向涡动转速区域可能超出临界转速分离区域。吴文青等[13]利用有限元法研究了大型汽轮机低压转子不平衡和弯曲响应特性,并分析了轴承对称特性对振动响应的影响。Rao等[14]为识别转子涡动方向,在振动测试系统中专门设计了复杂的计算电路,并通过试验证明了轴承间隙周向不均匀可导致Jeffcott转子反向涡动。王杰等[15]建立了双转子系统有限元模型,研究了轴承非对称系数对反进动转速区域的影响。综上,对不平衡离心力作用下的转子反向涡动问题的研究主要集中在临界转速分离区域,缺少对其他工作转速下反向涡动实测案例的介绍分析。
滑动轴承刚度非对称设计有稳定性高的优点,是大型汽轮发电机组轴系设计普遍采用的技术方案[11]。大型汽轮发电机组轴系较长,且冷热态中心变化大,各轴瓦载荷很难始终保持理想状态,可能使轴瓦在不同方向的刚度差异更为明显[16],此外,现实中发生的轴系质量不平衡通常为多面不平衡。基于上述特点,笔者通过简化模型的理论推导和现场实例分析,对不平衡导致的转子反向涡动问题进行研究。推导了使用相对轴振测量结果来判断轴颈涡动方向的数学表达式,建立了非对称支撑转子动力学分析简化模型,分析了不平衡质量的轴向位置、大小和所在角度对转子涡动方向的影响规律。
1 转子涡动监测
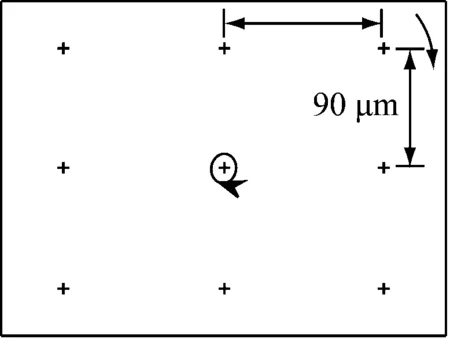
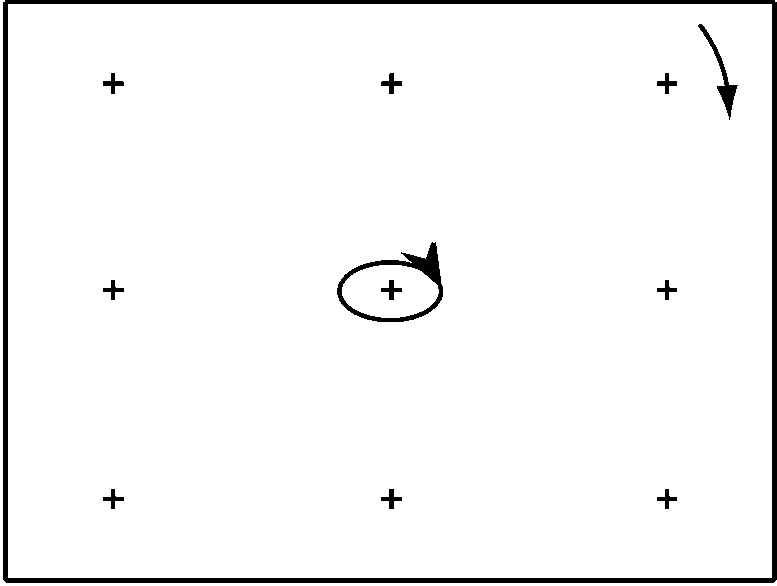
大型汽轮发电机组普遍配备轴系振动监测系统,典型传感器布置方式为每个轴承处安装夹角为90°的2个电涡流探头,如图1所示。采集的原始振动位移信号经过傅里叶分解,将2个方向位移的一倍频分量表示为:
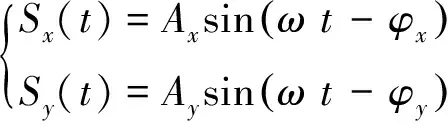
(1)
式中:Sx(t)、Sy(t)分别为轴径在X和Y方向位移的一倍频分量;Ax、φx分别为SX传感器测得的振动幅值和相位;Ay、φy分别为SY传感器测得的振动幅值和相位;ω为转子转动角速度;t为时间。

图1 转子涡动及振动测量系统示意图Fig.1 Schematic diagram of rotor whirl orbit and vibration measurement
设图1中固定坐标系Y轴与传感器SY的夹角为α,表示传感器的安装角。则此固定坐标系下轴心实时坐标(x,y)和轴振(Sx,Sy)之间的换算关系为:
(2)
转子涡动方向即图1中轴心轨迹中轴心的移动方向。当涡动方向和转子转动方向相同时为正向涡动,相反时为反向涡动[11,14]。设φ为轴心在固定坐标系中的方位角,根据图1中几何关系,有:
(3)
将式(1)、式(2)代入式(3)并对t求导数,得到方位角φ的变化率:
(4)
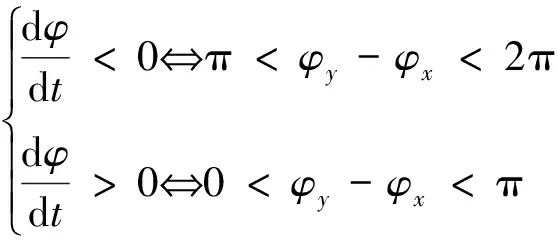
(5)
由式(5)可知,通过2个正交布置探头测得振动的相位关系即可判断转子涡动方向。由于式(4)中不含传感器安装角α,表明截面上2个传感器只需保持相互垂直,安装角不影响涡动方向的判断结果。
2 非对称支撑转子系统响应分析
图2为非对称支撑转子简化模型示意图。对实际模型进行简化,使系统在X方向和Y方向上的自由度能够解耦,忽略轴承刚度和阻尼的交叉项,也不考虑陀螺效应的影响。模型中转子为轴对称,轴承在X、Y方向具有不同的刚度(记为Kx、Ky)和阻尼(记为Cx、Cy)。
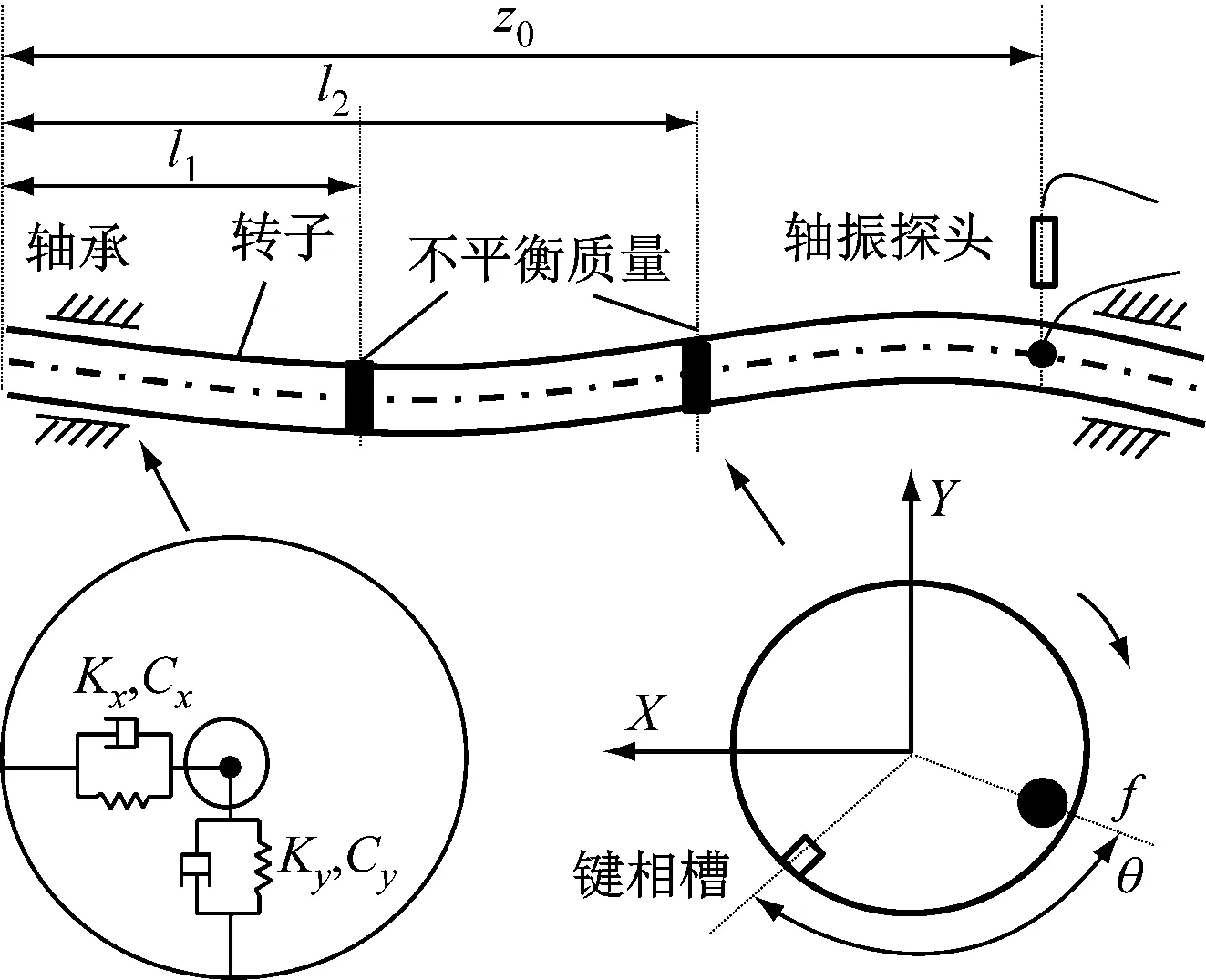
图2 非对称支撑转子简化模型Fig.2 Simplified model of non-axisymmetric support-rotor
由于系统在刚度不同的2个方向是解耦的,设X方向第i阶固有频率为ωx,i,Y方向第i阶固有频率为ωy,i,分别对应主振型φx,i和φy,i。若2个方向上有前n阶模态需要考虑,根据模态叠加法,轴向坐标为z处截面轴心位移可表示为:

(6)
式中:ηx,i(t)和ηy,i(t)分别为X方向和Y方向的第i阶正则坐标。
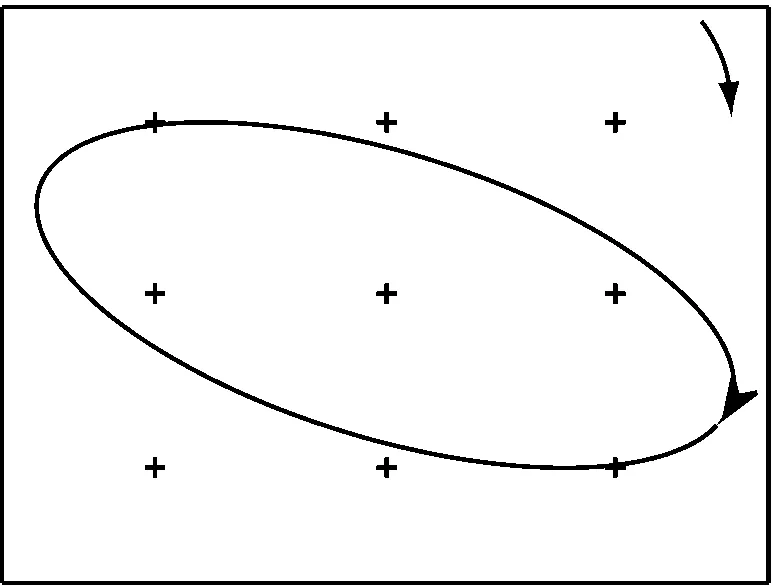
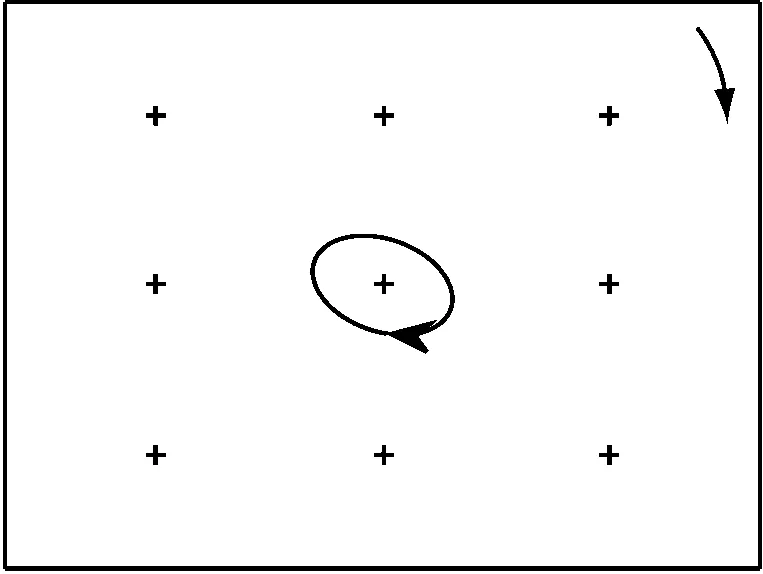
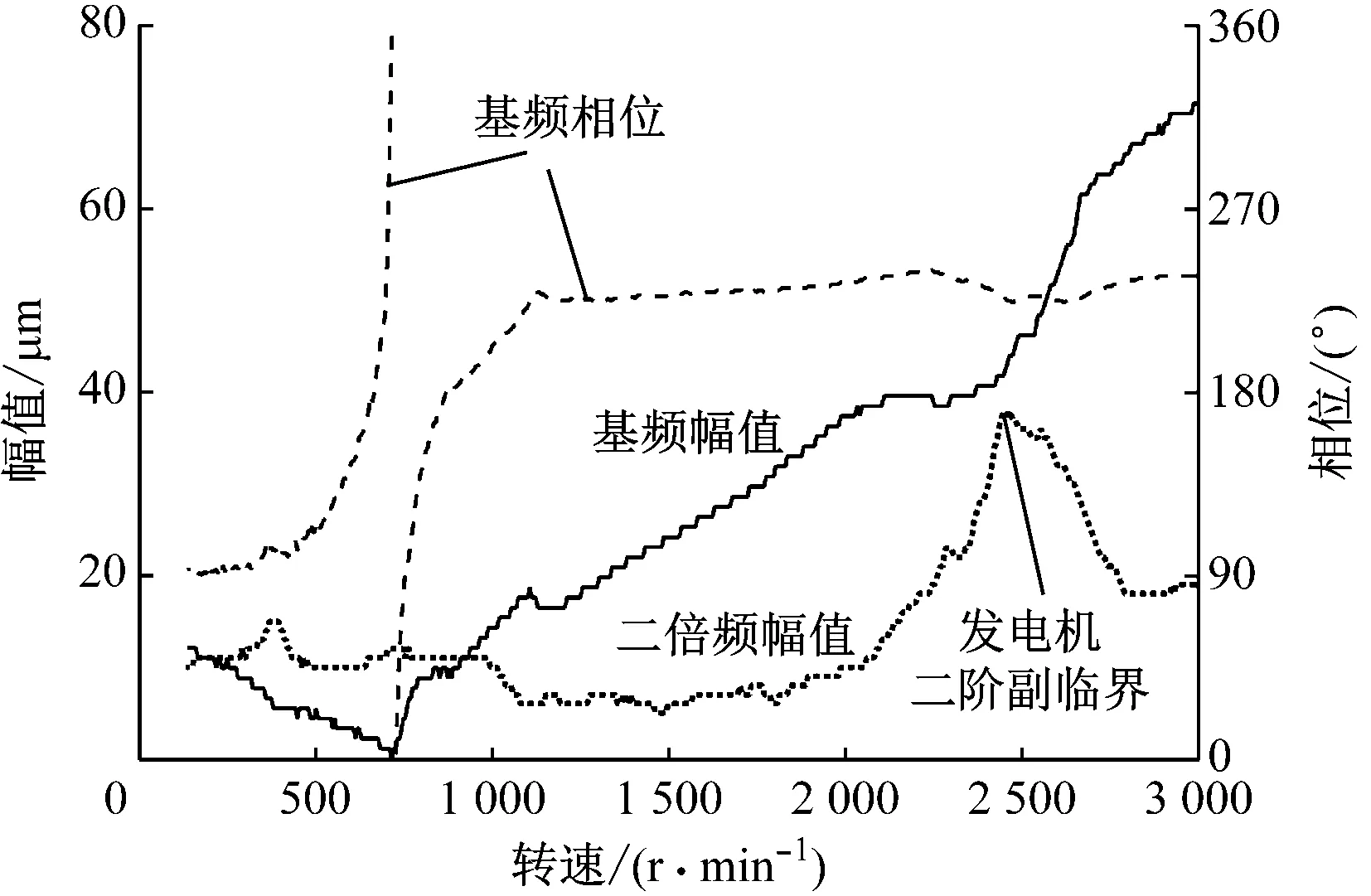
当忽略轴承非对称特性时,转子系统固有频率成对出现,即ωx,i=ωy,i,也分别对应OXZ和OYZ平面内的相同振型。2个方向刚度不同时,原先重合的固有频率分离,一个对应刚度小的方向,另一个对应刚度大的方向。不失一般性,假设Kx (7) 式中:qx,i(t)和qy,i(t)分别为X方向和Y方向第i个正则坐标的广义力;ξx,i和ξy,i分别为X方向和Y方向第i阶模态阻尼比。 如图2所示,转子轴向位置l1处有大小为f1、相位为θ1的不平衡激振力,X方向和Y方向的不平衡力Qx,1和Qy,1可用复数表示为: (8) 对应的正则坐标下的广义力为: (9) 将式(9)代入式(7)得到第i组正则坐标方程为: (10) 求解方程组(10),得到当转子轴向位置l1处有大小为f1、相位为θ1的不平衡激振力时,X方向第i阶正则坐标方程的解为: (11) 将式(11)代入式(6)可得: Sx(z,t)= f1ei(ω t-θ1)Cx(l1,z) (12) 式中:Cx(l1,z)为在l1处0°位置加重单位质量时,在转子z处X方向的响应,即通常所说的l1处加重对测量截面处X方向振动的影响系数。 Cx(l1,z)= (13) Cy(l1,z)= (14) 根据线性叠加原理,当在轴向l1和l2位置分别有不平衡量G(l1)和G(l2)时,转子z0处的不平衡响应为: (15) 从式(13)和式(14)可以看出,当n>2,且l1、l2和z0不在振型节点时,影响系数满足以下关系: (16) 在式(16)的前提下,由式(15)可知,对于任意一组振动Sx(z0)和Sy(z0),都有唯一的一组加重方式与之对应。因此,必然有加重方式G(l1)和G(l2)使转子z0处的Sx(z0)和Sy(z0)满足任何相位关系,包括满足式(5)定义的反向涡动情形。 (17) 与式(16)类似,只要满足 (18) 则必然存在加重方式G(l2),使加重后Sx(z0)和Sy(z0)满足任何相位关系,包括满足式(5)定义的反向涡动情形。 神华神东电力新疆准东五彩湾发电有限公司(以下简称神华五彩湾电厂)3号机组汽轮机为间接空冷、超超临界、三缸两排汽660 MW汽轮机,配以水氢氢冷型发电机。汽轮机各转子为双支撑,发电机-集电环转子为3支撑结构,轴系简图见图3。 机组于2019年底进入整套启动试运行阶段。机组调试冲转到3 000 r/min后,9号轴承处相对轴振偏大,振动最大的9X测点峰峰值超过110 μm,超出了新机投产的振动保证值。现场振动测试结果显示振动以基频分量为主,3 000 r/min空载工况下振动幅值和相位相对稳定。表1给出了机组定速3 000 r/min空载工况下轴系8号和9号轴承处的振动数据。分析认为振动偏大的原因为轴系存在一定的质量不平衡,可以通过现场高速动平衡降低9号轴承轴振水平。 图3 660 MW汽轮发电机组轴系简图Fig.3 Schematic diagram of 660 MW turbine generator set 为了排除轴颈表面存在不圆度、材质不均和局部剩磁对振动信号的影响,本文3个案例中振动数据已扣除200 r/min下测得的晃度。 经计算,提供动平衡方案为9号轴承后平衡盘330°位置加重230 g。在调试过程停机窗口实施加重,方案实施后轴系振动水平显著降低,相同工况下各测点振动均在50 μm以下,相关测点振动数据见表1。根据第1节中提出的涡动方向判定准则,比较X方向和Y方向的轴振基频相位,可以看出平衡前8号和9号轴承处均为正向涡动,平衡后9号轴承处轴颈为反向涡动。图4给出了机组动平衡前后8号和9号轴承处轴心涡动轨迹,图4(d)验证了平衡后9号轴承处轴颈涡动方向为反向。 华能营口电厂3号机组为600 MW超超临界汽轮发电机组,投产于2007年。其汽轮机为高中压合缸,较图3中机型少2个轴承,因此集电环前后为6号和7号轴承。机组于2017年经历一次A级检修后于4月24日启动,定速3 000 r/min后测试结果显示7X和7Y测点峰峰值均在130 μm以上,超过了报警值。利用机组检修后试验过程中短期停机机会,现场对集电环小轴提供高速动平衡方案,在集电环尾部平衡槽上加重200 g∠85°。 表2给出了加重前后6号和7号轴承振动数据,动平衡处理后,轴系6号和7号轴承处振动均显著降低。图5为该发电机组动平衡前后6号和7号轴承处轴心涡动轨迹。从图5中的轴心涡动轨迹和表2中的基频振动相位都可以看出,动平衡处理后7号轴承处轴颈为反向涡动。 表1 神华五彩湾电厂3号机组动平衡前后振动数据 (a) 8号轴承平衡前 (b) 8号轴承平衡后 (c) 9号轴承平衡前 (d) 9号轴承平衡后图4 神华五彩湾电厂3号机组动平衡前后8号和9号轴承处轴心涡动轨迹Fig.4 Shaft whirl orbit at No.8 and No.9 bearings before and after dynamic balance of No.3 unit of Shenhua Wucaiwan Power Plant 表2 华能营口电厂3号机组动平衡前后振动数据 (a) 6号轴承平衡前 (b) 6号轴承平衡后 (c) 7号轴承平衡前 (d) 7号轴承平衡后图5 华能营口电厂3号机组动平衡前后6号和7号轴承处轴心涡动轨迹Fig.5 Shaft whirl orbit at No.6 and No.7 bearings before and after dynamic balance of No.3 unit of Huaneng Yingkou Power Plant 新疆准东特变能源有限责任公司(以下简称准东特变电工)1号机组与案例一机型相同,轴系简图如图3所示。在3 000 r/min工况下9号轴承X方向相对轴振超过220 μm,不满足长期运行的要求。2020年10月27日,对1号机组带负荷稳定运行、滑参数降负荷及惰走过程进行了详细振动测试。测试期间机组9号轴承X方向轴振最高达到237 μm,振动主要为基频分量,幅值约有50 μm的波动。 根据振动测试结果,发电机-集电环转子振动以基频分量为主,为质量不平衡导致的强迫振动。基频振动的幅值和相位在不同工况下有所变化,表明其平衡状态也受工况影响,为不稳定的质量不平衡问题。由于幅值和相位在一定范围内波动,分析认为可以尝试通过现场高速动平衡的手段改善其振动水平。根据现场振动测试结果,为降低1号机组在带负荷工况下9号轴承处的轴振幅值,现场计算并给出了动平衡方案,加重位置为集电环小轴尾部平衡盘。在集电环小轴尾部平衡盘加重245 g,加重后满负荷工况下,各测点振动均在70 μm以下,如表3所示。与前2个案例相似,加重后9号轴承处轴颈同样为反向涡动。图6为该机组动平衡前后8号和9号轴承轴心涡动轨迹。 表3 准东特变电工1号机组动平衡前后振动数据 本节中的3个案例对应于第2节中分析的第二种情形,即式(17)和式(18)对应的情况,如果平衡前振动矢量与加重影响系数不成比例,则可能出现加重后轴颈为反向涡动。表4为发生反向涡动轴承处的轴颈振动数据。表5给出了轴径发生反向涡动轴承处相位差和涡动方向。以案例一为例,初始振动矢量和影响系数如下: (a) 8号轴承平衡前 (b) 8号轴承平衡后 (c) 9号轴承平衡前 (d) 9号轴承平衡后 (19) 表4 案例中发生反向涡动轴承处轴颈振动数据 表5 案例中发生反向涡动轴承处轴颈振动特征 将式(19)中数据变换为复数形式后代入式(18),可知行列式不为零,即只要在集电环后平衡盘配重的大小和角度满足一定关系,9号轴承处轴颈就会出现反向涡动。根据式(5)和式(17)可知,转子在z0处发生反向涡动的充分必要条件是π<φy-φx<2π,即 (20) 为了方便表示,加重矢量表示形式由“重量∠角度”变为“实部+ i×虚部”。图7给出了9号轴承2个方向上的振动相位差与加重矢量之间的关系。从图7可以看出,存在小部分区域使相位差处于180°以上,对应转子为反向涡动。 图7 振动相位差与加重矢量之间的关系Fig.7 Relationship between the difference of the vibration phase angle and the balance vector 把发电机和集电环转子看成一个整体时,工作转速下轴系振动受4个模态影响。在3 000 r/min以下有2个临界转速,分别对应发电机转子主导的一阶和二阶振型。在3 000 r/min以上有发电机转子三阶和集电环小轴一阶临界转速。 图8为案例一中发电机前轴承Y方向(7Y)轴振BODE图。从图8可以看出,在0~3 000 r/min范围内,7Y轴振一倍频峰值出现在769 r/min和2 053 r/min,分别为发电机转子的一阶和二阶临界转速。由于发电机转子开线槽导致刚度不对称,转速接近模态频率0.5倍时可能出现的二倍频振动峰值,对应转速为副临界。在1 025 r/min和2 570 r/min出现了7Y轴振二倍频分量峰值,分别对应于发电机转子二阶和三阶临界转速的0.5倍,因此推测其三阶临界转速为5 140 r/min左右。可以看出,此机型工作转速对发电机二阶和三阶临界转速都有较好的避开率。 图8 案例一中发电机前轴承7Y轴振BODE图Fig.8 BODE diagram of 7Y shaft vibration of the inboard bearing of the generator in case one 图9为案例一在升速过程中集电环9Y轴振BODE图。从图9可以看出,9Y轴振基频幅值在3 000 r/min以下没有出现峰值,且9Y基频相位在靠近3 000 r/min时也比较稳定,初步判断未靠近临界转速区域。因此,根据3 000 r/min以下振动数据,暂时可认为工作转速避开了集电环小轴的一阶临界转速区域。 图9 案例一中集电环轴承9Y轴振BODE图Fig.9 BODE diagram of 9Y shaft vibration of collector ring rotor bearing in case one 从3个案例数据可以看出,此类型机组尾部平衡盘加重对集电环轴承X方向和Y方向的轴振响应灵敏度数据比较离散。初始振动多为跨内连续分布不平衡质量或轴轻微弯曲引起,与尾部平衡盘加重对末端轴承2个方向响应灵敏度往往不一致。因此,平衡前振动矢量和加重影响系数大概率会不成比例,可能出现加重后轴颈为反向涡动的情形。 (1) 振动以基频分量为主时,可以利用正交布置的传感器测得的基频相位来判断轴颈涡动方向,相位差小于180°时为正向涡动,相位差大于180°时为反向涡动。 (2) 若轴系某一截面处平衡前振动矢量和加重影响系数不成比例,则可能出现加重后轴颈反向涡动。对大型汽轮发电机-集电环的3支撑轴系结构测试及动平衡总结发现,初始振动与尾部平衡盘加重对末端轴承2个方向的响应灵敏度往往不一致,容易出现动平衡后轴颈为反向涡动的情况。 (3) 由于大型汽轮发电机组轴系复杂,有多阶模态会影响工作转速下的振动,其轴承又有不对称特性,当存在分布式或者多面的质量不平衡时,仅不平衡质量离心力这一正向激振力就可以引发轴颈在工作转速下的反向涡动。
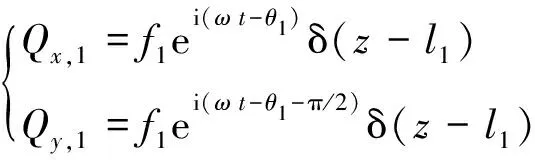

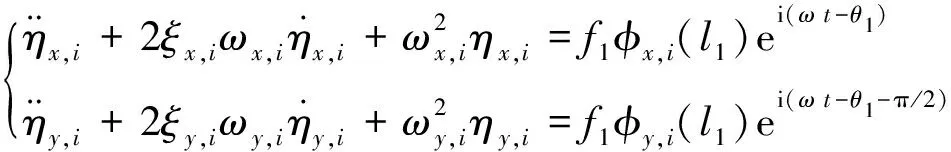

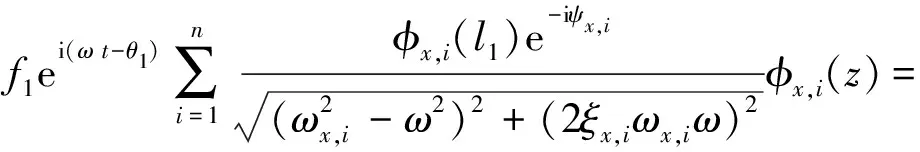

3 轴颈反向涡动现场案例
3.1 案例一

3.2 案例二








3.3 案例三

3.4 实测反向涡动原因分析







4 结 论
