高动态条件下星斑模拟与星点提取方法

潘迪，周琦，刘轩，刘冰，方慧

（上海航天控制技术研究所上海市空间智能控制技术重点实验室，上海201109）

0 引言

星敏感器是以恒星为参照物的高精度姿态敏感器，通过探测器对星空成像获取星图，测量恒星矢量在星敏感器坐标系中的分量，并利用已知恒星的精确位置来确定航天器相对于惯性测量系的三轴姿态［1］。为了从星图中获得更高的星点定位精度，星敏感器的光学系统常常采用离焦的方式，使得静态条件下星点在探测器成像面上的像斑扩散为3×3 至5×5 的弥散圆［2］，接着再利用细分定位算法提取星点质心，精度可达到亚像元级［3］。但是，随着航天技术的发展，导弹、临近空间飞行器等机动性强、运动角速度大的运载体对星敏感器的动态性能提出了更严格的要求［4］。

在高动态情况下，星点和探测器像平面会发生相对运动，此时星点像斑不再是弥散圆，而呈现出拉长的条带状，这种现象称为星点像斑的“拖尾”［5］。在曝光时间内，像平面接收的光电子总数不变，但随着拖尾现象的发生，星点能量分散到更多的像元内，从而导致星点成像的模糊及断裂。星点的“拖尾”、模糊和断裂都使得传统方法无法准确提取星点质心，从而对航天器的定姿产生重大影响。

高动态下的星点目标提取及质心定位技术是近年来研究的热点。WU Xiaojuan 等［6］提出了分布复原的方案去除多重星图模糊，但是上天件的处理器计算能力有限，多次采用卷积运算无法满足实时性的要求。JIN Yan 等［7］则针对星点“拖尾”现象提出了一种基于自适应窗口选择的星体目标提取方法，并基于数学形态学使断裂星体进行“主动生长”，完成了对于星斑的修补，但修补方法仅基于数学形态，没有考虑像斑的真实灰度分布情况，容易造成像斑失真，尤其对于星斑呈现为有斜率的直线时，该方法的提取精度并不理想。LIAN Da 等［5］建立了动态条件下的恒星成像模型并利用模板补偿星斑缺失部分，有效提高了星点质心定位精度，但动态模板生成时采用的静态模板是采用卡尔曼滤波实时估计出来的，且动态模板生成时采用了卷积方法，这样多重的复杂运算难以满足实时性的要求。

针对高动态下的星点拖尾问题，本文提出了一种高动态条件下星斑建模及星点目标提取方法，首先建立高动态下星点像斑拖尾的数学模型，接着阐释星跟踪模式下利用相关模板匹配法和质心法提取星点质心的方法，最后使用外场观星实验的数据完成了算法的仿真，验证了算法的有效性。

1 高动态条件下星点像斑拖尾模型

1.1 静态星点像斑模型

星敏感器探测的目标恒星相对于光学系统焦距来说可视为无穷远。理想情况下，探测器成像面上静态星点像斑的能量分布符合二维高斯分布［8-9］

式中，I(x，y)为探测器成像平面坐标为(x，y)的像元所接收的光电子数，(x0，y0)为星点质心，σ为高斯半径。Ne为在曝光时间T内，探测器平面上接收的光电子总数，表示为

式中，ρe为探测器激发电子数密度，和探测器的量子效率有关，不同光谱型恒星的激发电子数密度可由地面实验计算拟合得出。φ为入瞳孔径，T为曝光时间，Mv为恒星的视星等。

随后将光电子数量化为灰度值，则静态星点像斑的数学模型如式（3）所示，示意图如图1所示。

图1 静态星点像斑模型Fig.1 Static star spot model

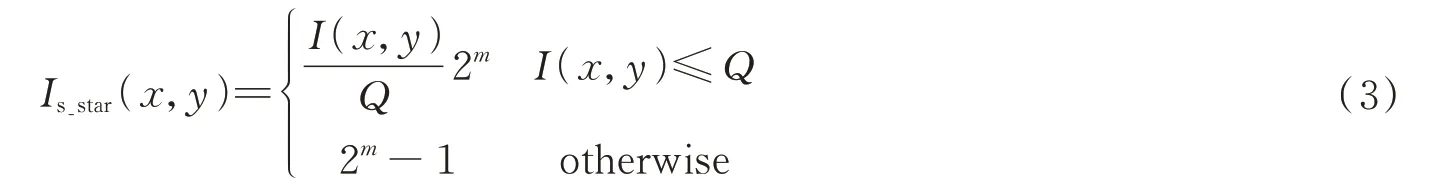
式中，Is_star(x，y)为探测器成像平面坐标为(x，y)像元的灰度值，m为量化系数，Q为像元电子满阱容量。

由于恒星的辐射特性以及星敏感器的光学系统参数在短时间内可视为恒定，所以，在静态稳定条件下，某一特定恒星在星敏感器探测器上的成像像斑在一定时间内是确定的。因此，为了节省星敏感器的存储空间，对于导航星表中的恒星，可在地面由式（1）～（3）计算出理论的m×m静态星斑模板矩阵并存储于导航星表中，以供后续动态像斑建模时使用。以某型星敏感器为例，其探测器像元尺寸为18 μm，光学系统保证的均方根弥散斑半径为25 μm，则恒星在该探测器上成像的弥散光斑有80%以上的能量集中于3×3 的像元内，所以如图2所示，可在地面计算理论的3×3 静态星斑模板矩阵并存储于导航星表中。

图2 导航星表中的静态星点像斑模板Fig.2 Static star spot model in guide star catalogue

1.2 高动态星点像斑模型

高动态条件下，星点能量不再集中于弥散圆中，而是会在邻域的若干个像元上产生灰度分布［10］。由于短时间内星点的运动可视为匀速运动，所以在拖尾区域内，星点能量分布关于二维平面位置的函数关系变为

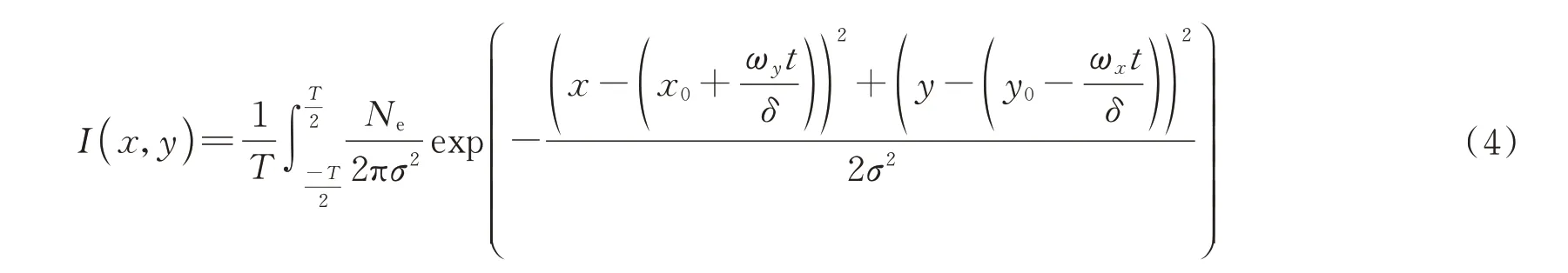
式中，(x0，y0)是自定义曝光中点时刻坐标，ωx和ωy分别表示星敏感器绕x轴和y轴的角速度，δ为像元角分辨率，T为曝光时间，其他参数含义同式（1）。但是，上天件的处理器并不能实时计算复杂的积分运算，所以需要对式（4）进行优化。由于星敏感器的曝光时间一般小于100 ms，星斑在探测器平面上的运动等效为匀速运动，星斑的总能量均匀地分布在星点质心划过的轨迹上，则可将动态星点拖尾像斑看作是恒星静态像斑在曝光时间内累加并均分能量的结果，如式（5）所示。

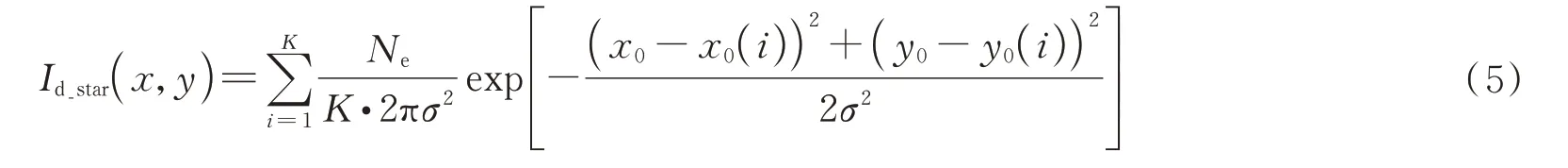
式中，(x0(i)，y0(i))表示曝光时间内第i个星点质心在探测器上的坐标，K为累加次数。现在问题就转化为如何在探测器平面上求取星点质心坐标的离散轨迹。

由于探测器由一个个像元组成，当要在探测器上生成一条直线时，可以使用Bresenham 直线生成算法［10］来解决如何选择最佳的一组像元坐标集合来表示星点质心位置的问题。算法的输入为直线的起点、终点坐标，通过维护一个误差量参数来确定下一个像素点的位置。

使用Bresenham 算法生成动态星点像斑模板的流程如图3所示。

图3 动态星点像斑模板生成流程图Fig.3 Flow diagram for dynamic star spot template generation

首先按式（6）计算星斑在探测器像平面上的模糊长度［11-12］

式中，Lx和Ly分别表示在探测器像素坐标系x轴方向和y轴方向上的模糊长度，由于Bresenham 算法中只涉及整数运算，所以Lx和Ly要附加取整运算。ωx，ωy分别表示星敏感器绕测量系x轴和y轴的角速度，可由陀螺输入。T为曝光时间，f为光学系统焦距，Dp为像元尺寸。文献［11-12］推导了载体运动对星点成像的影响，并证明当三轴角速率处于同一量级时，星敏感器绕z轴转动产生的星斑拖尾长度与绕x轴、y轴相比至少降低了一个数量级。又因为载体姿态机动速度分在星敏感器的三个轴上，小概率会出现载体只有z轴有大速度的情况，所以，本文在生成高动态星斑模板时，只考虑绕x轴和y轴旋转的情况，即认为星点质心在曝光时间内形成的轨迹近似为直线。

接着，计算模糊轨迹的斜率

定义轨迹的起点坐标(xs，ys)和终点坐标(xe，ye)，使其满足关系

要注意的是，这里的起点、终点坐标并不是星斑轨迹在探测器上真实的起点终点坐标，仅是在生成像斑模板时的假设，理论上可以取满足式（8）的任意值。将(xs，ys)、(xe，ye)代入Bresenham 算法中，得到星点轨迹质心坐标集合及坐标个数n。遍历集合中的坐标，以第i个坐标为中心，Mtem为模板建立累加基础矩阵。其中，Mtem为2.1 节所述导航星表中存储的静态星斑模板矩阵。将每一个累加基础矩阵相加并平均化能量，则最终生成的动态星斑模板为

式中，w表示动态星斑模板矩阵。

考虑到星跟踪模式下星敏感器波门尺寸有限，对于模板尺寸有一定的要求。若要生成M×M的动态模板，则需先计算轨迹起点及终点坐标的中点，并以之为中心截取M×M的矩阵，即可得到最终的动态星点模板。动态像斑生成过程如图4所示（此时模板尺寸设置为7×7）。

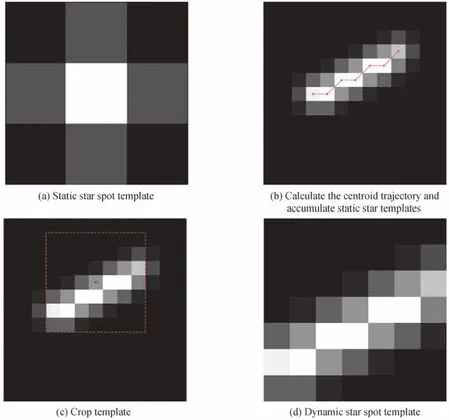
图4 动态星斑模板生成过程Fig.4 Dynamic star spot generation process

需要说明的是，使用本方法生成的星斑模板并不能准确反映星斑的能量分布，只是对其的一种近似。本文生成动态模板的目的是在星跟踪模式下对波门内的拖尾星斑使用相关模板匹配法进行粗定位，需要兼顾速度和精度的要求，而使用积分运算的“复杂模板”虽然可以准确模拟星斑的能量分布，但无法满足上天件实时性的要求。而使用本文算法生成动态模板的过程中只涉及整数运算，不存在浮点数，大大挺高了计算效率。使用相关模板匹配法进行星点提取的方法将在第三节介绍。

2 高动态条件下的星点提取

在传统的星跟踪模式下，星敏感器根据前几帧的姿态信息，采用运动矢量估计的方法预测当前帧导航星在像面上投影的位置，并以该位置为中心开波门，然后采用阈值分割与连通域法［5］提取星点质心。如果波门中能够提取有且只有一个星点，则将该星点与导航星相匹配，星跟踪成功。如果波门中没有星点被提取出或提取的星点不唯一，则丢弃该波门。在低速条件下，为了保证星点的提取率，波门尺寸不宜过大，一般取8×8 至10×10。而在高动态情况下，运动矢量估计不准确，预测的导航星位置容易出现较大偏差，此时需要适当扩大波门尺寸。由于星斑能量的分散和星斑断裂，如果直接采用阈值分割与连通域法提取质心，波门内容易提取不出或提取出多个四连通域，此时就无法准确提取星点质心。

针对阈值分割和连通域法在高动态下无法准确提取星点质心的问题，本文提出一种星跟踪模式下波门内星点质心提取方法，以2.2 节生成的动态星斑模型为模板，结合相关模板匹配法在星跟踪波门内进行星体粗定位，接着进行伪星点剔除，最后在星点粗定位区域使用质心法提取质心，这样由粗到细的质心提取方法，能够克服传统法在高动态、大波门情况下星点提取率低、质心提取精度不高的问题。

2.1 星跟踪模式下的星体目标粗定位

模板匹配是一种图像处理技术，通过在输入图像上滑动模板将模板子图和全图进行匹配，输出全图与模板的匹配矩阵［13］。匹配的方法有多种，本文选取相关匹配法。对于尺寸为N×N的波门图像f和尺寸为M×M的动态星斑模板w，将二者做卷积运算，输出相关性矩阵c为

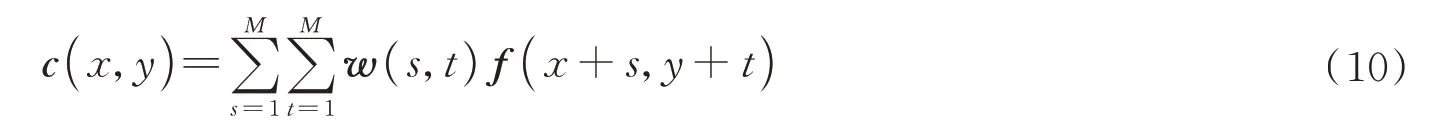
相关性矩阵中的元素代表波门子图与模板的相关性，数值越大则表示二者越相似。最大响应点(xmax，ymax)即为波门最佳匹配区域的左上角坐标，最佳匹配区域也就是星点粗定位区域H为

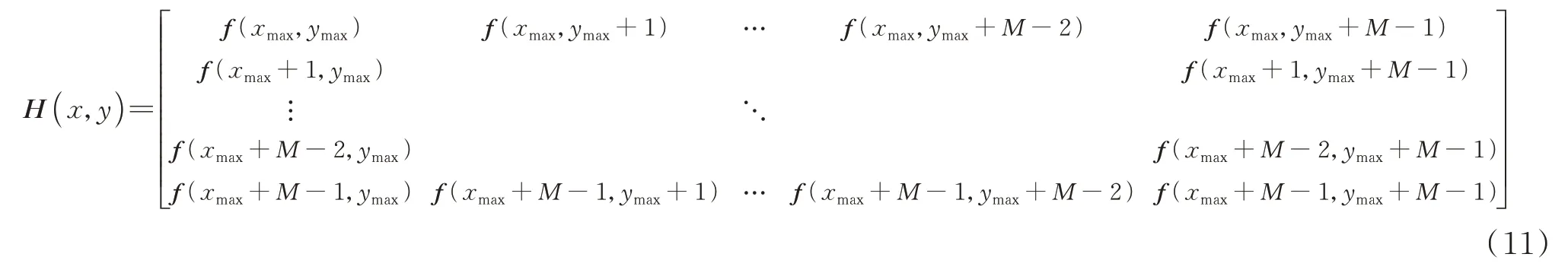
高动态条件下由于星点能量的分散及噪声的影响，信噪比降低，但是星斑的能量分布大致保持不变，相关性匹配能够找出与模板灰度分布最相似的区域，以此实现星点目标的粗定位。

2.2 伪星点剔除

对于一幅波门图像和一个星斑模板，二者进行相关性匹配后，总会在相关性矩阵中找到最大响应点。但有时波门中可能并没有星点存在，而相关匹配法还是会通过最大响应找到“伪星点”，造成星点的误检。此时需要设定伪星点判据以降低误检率。

首先对星点粗定位区域H进行阈值分割

式中，bkg 是星点粗定位区域内所有像元的灰度均值，offset 是偏移量，在轨可调，默认值可依据工程经验确定。

接着对阈值分割后的图像进行二值化

最后统计二值化矩阵Hbi(x，y)中像素值为1 的有效像素数Np。如果Np＞Thstar，则认为该区域中存在星点，可进行后续的星点细分定位运算；反之，则判定该波门内无星点存在，丢弃该波门。其中，Thstar为伪星点剔除门限，在轨可调，默认值可依据工程经验设定。

2.3 星点质心细分定位

3 实验结果与分析

3.1 实验条件

实验采用的数据为某型号星敏感器2021年7月31日的外场地面观星LVDS 下传的波门数据，某型号星敏感器的光学系统参数如表1所示，实验装置如图5所示。实验数据仅采用图片左侧星敏感器的实测数据。实验中所使用的导航星表，其视星等范围为-0.62～6.38。

表1 某型号星敏感器光学系统参数Table 1 Optical system parameters of the star sensor

图5 某型号星敏感器外场观星实验图Fig.5 Star sensor experiment diagram

实验分为两组，每一组皆分别使用“简易模板”相关匹配法（下述“简易模板法”）、“复杂模板”相关匹配法（下述“复杂模板法”）与传统的阈值分割及连通域法［5］（下述“传统法”）三种方法提取波门内星点质心。其中，“简易模板”为使用本文算法生成的动态星斑模板，“复杂模板”为使用式（4）计算的动态星斑模板。由于某型星敏感器能够适应的最短曝光时间为50 ms，角速度指标要求为3°/s，由式（6）和表1 可以计算得出，某型星敏感器在该极限条件下的星点拖尾长度为7.5 像元，所以实验中相关匹配法中所有星斑模板的尺寸皆设定为7×7，根据工程经验将伪星点阈值分割偏移量设为4，伪星点剔除门限设为7。这些物理量皆可根据在轨实际情况进行调整。在处理每一帧波门数据时，模板由处理器直接计算。两组实验中的每一次测试，皆选取星跟踪模式下的100 帧波门图像作为实验数据。

第一组实验，曝光时间设定为恒定值86 ms，设定转台转动速度，使星敏感器的合成角速率分别大约为1°/s，2°/s 和3°/s，测试三种星点提取方法在不同角速度下对星敏感器定姿精度的影响。第二组实验，转台转速设定为恒定值3.1°/s，设定三组不同的曝光时间86.5 ms，62.5 ms 和50 ms，测试三种星点提取方法在不同曝光时间下对星敏感器定姿精度的影响。

3.2 评价指标

本文采用星对角距误差、单帧提取率和计算时间作为算法的评价指标。

1）星对角距误差。在高动态情况下，传统的基于滑动窗口的误差计算方法［15］不再适用。本文鉴于星对角距的不变性，采用视场内星对角距统计偏差评估星敏感器的姿态测量精度［16］

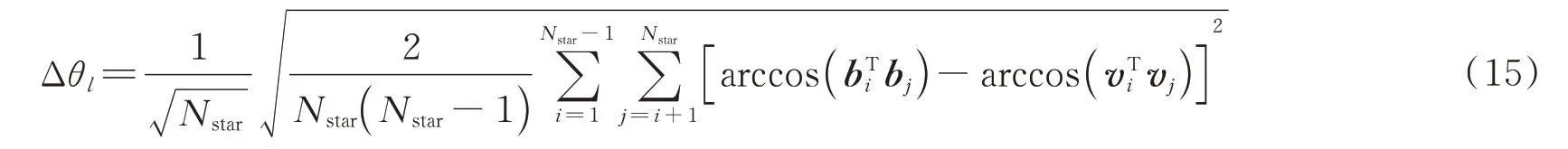
式中，Nstar为当前帧视场中的定姿星数，b和v分别为标准星矢量和测量星矢量，l代表帧号。

2）单帧提取率。单帧提取率为一帧中成功提取的探测星数与视场中所有导航星数的比值。若算法能够成功输出星点质心，则判定星点提取成功。

3）计算时间。算法处理100 帧波门所需时间。

3.3 实验结果

实验一的评价结果如表2～4所示，星对角距误差曲线如图6所示，其中星对角距误差统计了100 帧误差的均值和三倍标准差，提取率统计了100 帧提取率的均值、最大值和最小值。

图6 三种角速度下三种星点提取方法的星对角距误差曲线图Fig.6 Angle distance error curves of three star point extraction methods under three angular velocities

表2 “简易模板”相关匹配法在三种角速度下的实验结果Table 2 Experimental results of cross correlation template matching method using simple template at three angular velocities

表3 “复杂模板”相关匹配法在三种角速度下的实验结果Table 3 Experimental results of cross correlation template matching method using complex template at three angular velocities

表4 传统法在三种角速度下的实验结果Table 4 Experimental results of traditional method at three angular velocities

分析实验数据可得，在三种角速度下，简易模板法与复杂模板法相比，星对角距误差均值相当，单帧提取率相当，计算速度提升了500 多倍。可见高动态情况下，在使用相关匹配法提取星点质心时，使用本文算法生成的简易星斑模板是真实星斑模板在不牺牲精度条件下的近似替代。将简易模板法与传统法相比，从星对角距误差上来看，简易模板法的星对角距误差较为稳定，在角速度1°/s，2°/s 和3°/s 的高动态条件下，星对角距误差均值较传统法分别减小了30.5%，36.9%，49.8%。从提取率上来评价，相关匹配法能够稳定提取星点，100 帧的平均提取率在90%以上。而传统法提取率较低且不稳定，在角速度3°/s 时平均提取率已达不到80%。从计算速度上来评价，两种算法处理一帧波门数据平均需要40ms，满足实时性的要求。以上实验结果表明，使用简易模板的相关模板匹配法在高动态情况下能够实现恒星的稳定跟踪，且误差稳定，精度符合星敏感器的指标要求，速度满足实时性要求。

实验二评价结果如表5～7所示，星对角距误差曲线如图7所示。

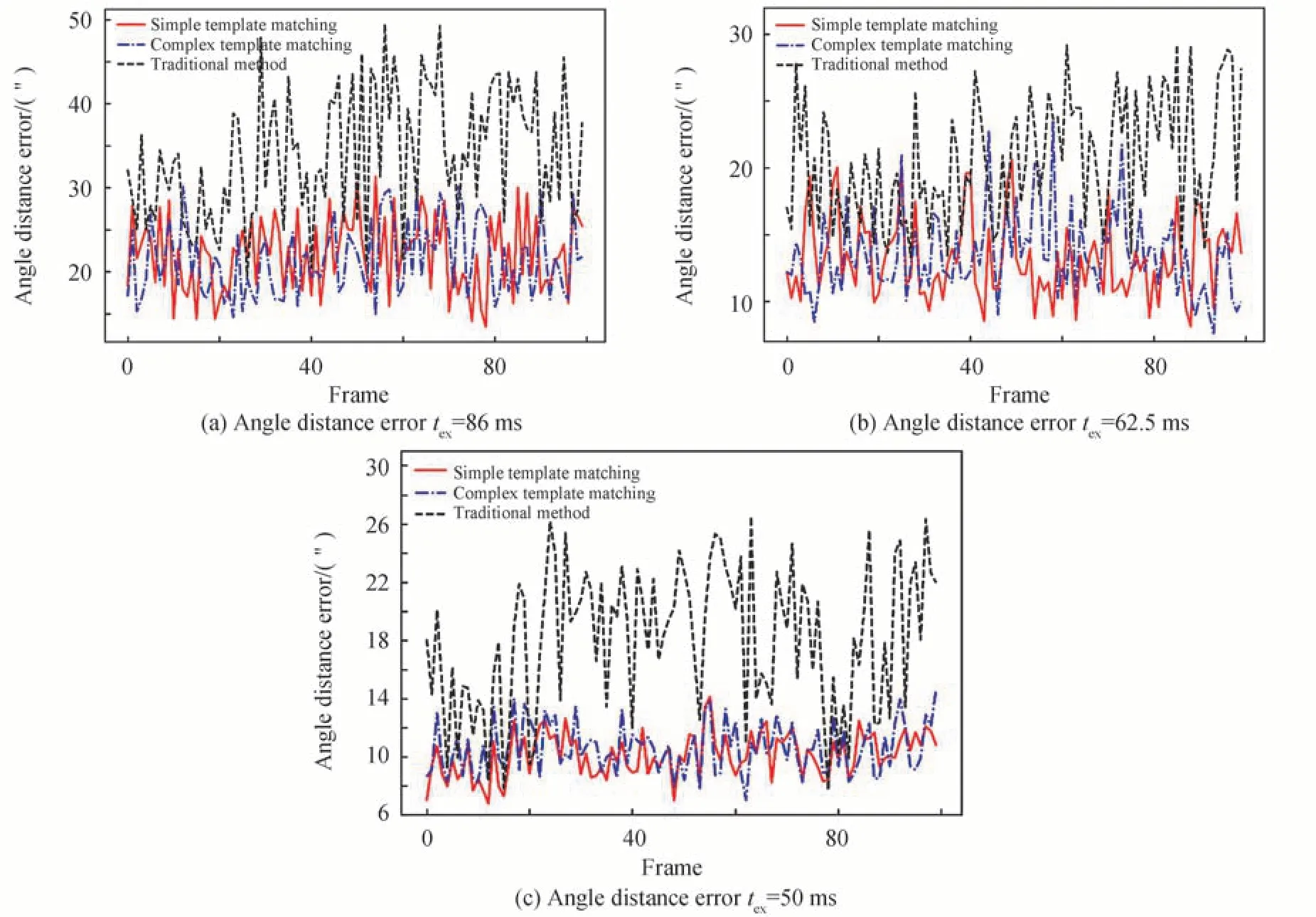
图7 三种曝光时间下三种星点提取方法的星对角距误差曲线图Fig.7 Angle distance error curves of three star point extraction methods under three exposure time

表5 “简易模板”相关匹配法在三种曝光时间下的实验结果Table 5 Experimental results of cross correlation template matching method using simple template at three exposure time

分析实验数据可得，在三种曝光时间下，简易模板法与复杂模板法相比，星对角距误差均值相当，单帧提取率相当。实验二同样证明了高动态情况下，简易星斑模板是真实星斑模板在不牺牲精度条件下的近似替代。将简易模板法与传统法相比，从星对角距误差上来评价，简易模板法的星对角距误差更稳定，在曝光时间为86 ms，62.5 ms 和50 ms 的条件下，误差均值较传统方法分别减小了53.8%，56.1%，78.4%。从提取率上来评价，对于三种曝光时间，简易模板法能保证提取率在90%以上，而传统法的提取率均值达不到

90%。从运算速度上来评价，两种算法运行速度相当，处理一帧波门需要约40ms，满足实时性要求。以上实验结果表明，简易模板相关匹配法在高动态下能够适应多种曝光时间，在实现稳定跟踪的同时提高定姿精度且计算速度满足实时性要求。在角速度3°/s 及曝光时间50 ms 的条件下，简易模板相关匹配法的星对角距误差均值为10”，平均提取率为97%。

表6 “复杂模板”相关匹配法在三种曝光时间下的实验结果Table 6 Experimental results of cross correlation template matching method using complex template at three exposure time

表7 传统法在三种曝光时间下的实验结果Table 7 Experimental results of traditional method at three exposure time

4 结论

本文针对高动态情况下星点目标提取困难的问题，提出了一种高动态条件下星斑模拟与星点目标提取方法。此方法首先建立静态星点像斑的数学模型，其次在已知星敏感器角速度的情况下使用Bresenham 直线生成算法生成高动态星点拖尾像斑模型，接着利用拖尾像斑模型和相关匹配法进行星体目标粗定位并剔除伪星点，最后再利用质心法在粗定位区域内提取星点质心。基于外场观星数据的仿真实验证明，本文算法生成的简易星斑模板是真实星斑能量分布在不牺牲精度条件下的近似替代。本文提出的星点提取方法能够实现星敏感器在角速率3°/s 条件下的稳定跟踪，并且能够适应各种长度的曝光时间。在曝光时间50 ms，角速度3°/s 的条件下，星对角距误差为10”，平均提取率为97%，相比于传统方法，分别提高了78.4%和36.6%。