硬塑粉质黏土层深埋马蹄形隧道开挖土拱演化分析

刘金慧 屈克军 丁万涛 王杨

摘要：硬塑状粉质黏土地层深埋马蹄形隧道开挖易出现土拱效应。以改进的太沙基围岩压力理论为基础，对上述马蹄形隧道开展了数值计算和现场监测试验，分析隧道开挖全过程中围岩竖向应力重分布及地层沉降变化情况，得出压力拱的形成及演化规律，并分析围岩力学参數大小变化对压力拱形态的影响。研究结果表明：压力拱内围岩应力及地层沉降变化显著，可作为压力拱高度和形状的判断依据;压力拱的形成与发展主要集中在掌子面前后约1倍隧道洞径的距离，它主要分布在隧道上方90°的区域;压力拱高度随围岩黏聚力及内摩擦角的增大呈明显的减小趋势，但宽度对围岩力学参数变化不敏感。研究成果为确定硬塑状粉质黏土地层深埋马蹄形隧道的超前支护参数提供了参考，对指导隧道施工具有重要意义。

关 键 词：马蹄形隧道; 土拱效应; 硬塑状粉质黏土地层; 竖向应力

中图法分类号： U459.3   文献标志码： A

DOI：10.16232/j.cnki.1001-4179.2022.01.029

0 引 言

隧道开挖后，围岩初始应力场发生改变，围岩自我调节形成新的二次应力场[1]。围岩应力重分布过程中，如果应力超过围岩强度，隧道周边围岩将首先发生破坏，并逐步向围岩深部发展，直至达到新的应力平衡，此时围岩产生一定的松动范围，称其为松动区[2]。由于围岩颗粒间存在黏结力和摩阻力，隧道开挖后围岩产生不均匀位移，松动区围岩将压力传递给相邻不动部分岩体，这种荷载传递作用称为土拱效应[3-4]，土拱效应的存在有效地提高了隧道整体稳定性[5]。

近年来大量工程与试验表明，隧道围岩破坏是一渐进性过程，围岩中土拱的形成和发展与围岩失稳密切关联，因此，国内外众多学者开展了土拱效应对隧道围岩的稳定性影响研究。吕玺琳等[6]通过开展3组饱和圆砾地层盾构隧道开挖面稳定性物理模型试验，发现当覆盖层达到一定厚度时，大尺寸圆砾间锁固形成土拱。代仲海等[7]发现盾构穿越紧邻隧道时，当盾构开挖面稳定后不同地层中掘进产生的土拱效应会减小所需的开挖支护力。刘克奇等[8]基于滑移线理论和极限分析上限定理，利用空间离散技术提出了一种考虑土拱效应的盾构施工掌子面三维滑移破裂模型，该模型的掌子面破坏区域形态更加接近离心试验结果与数值计算结果。白维仕等[9]基于滑移线网络法对黄土隧道坍塌拱及其承载力进行了分析，认为黄土的内摩擦角和黏聚力对黄土隧洞围岩坍塌范围及土拱极限承载力影响不同。陈强等[10]针对目前对土体中土拱形态假设众多、土拱形态的演变研究的不足，利用室内模型装置对土拱的形态和演变规律进行了试验研究。徐超等[11]利用模型试验研究了不同加载条件对土拱效应的影响。徐长节等[12]考虑松动区内部主应力轴偏转对松动区土体应力均匀分布的影响，对传统的土拱效应理论进行了修正。李瑞林等[13]针对现有理论较少关注非极限状态的土压力计算的问题，建立了考虑土拱效应的滑移面间非极限状态土压力计算模型。娄培杰等[14]考虑土拱效应，通过薄层微分层析法，给出了浅埋隧道的松动土压力计算公式。白廷辉等[15]研究了软土深部盾构开挖地层损失率对软土土拱效应的影响。陈其志等[16]通过设计室内挡板下落模型试验装置，研究了砂土中松动土压力及松动区位移破坏形式。陈强等[17]通过室内平面应变条件下的模型装置实现土拱形态的可视化，探究了砂性土中土拱演变阶段及影响因素。徐东等[18]通过土工离心模拟试验，探讨了上海黏土的成拱能力。路德春等[19]利用二次开发后的ABAQUS对隧道开挖过程进行了三维有限元分析，从不均匀变形、应力重分配、应力路径和地表沉降规律4个方面研究了由重力引起的大主应力改变产生的土压力拱效应。崔蓬勃等[20]基于主应力偏转理论，推导出不同土拱效应发挥程度下松动土压力及盾构极限支护力的计算公式。Terzaghi[21]通过活动门试验证实了岩土力学领域土压力拱效应的存在，认为土压力拱效应是由于土体的不均匀位移引起的，土压力拱的形成改变了土体中荷载的传递路径，引起应力重分布，并把作用于拱上的荷载传递到拱脚及周围岩土介质中去。Nakai等[22]利用离心机模型试验研究了土压力拱效应，利用数值方法分析了衬砌结构上围岩压力的分布规律。Lee等[23]通过离心模型试验和数值方法，研究了软黏土中开挖隧道时的土拱效应与隧道的稳定性。喻波等[24]通过数值方法，分析了隧道开挖围岩土压力拱的形成过程，并以隧道洞顶上部围岩能否形成稳定的压力拱作为隧道深、浅埋的划分标准。郑颖人等[25]以等效塑性剪应变作为失效准则，通过模型试验与数值模拟方法，研究了隧道围岩的破坏模式和深埋、浅埋的划分标准。Chappell[26]认为隧道开挖会导致围岩变形和应力重分布，其所产生的土拱可以对隧道围岩起到稳定作用。Lin[27]借助数值模拟手段通过分析隧道开挖过程中的土体应力重分布规律，进而研究隧道土拱演变规律。孙潇昊等[28]通过模型试验与颗粒流程序（PFC2D）研究了不同埋深下隧道土拱效应的差异。

目前尚无能够直接观测土拱厚度与形状的试验手段，数值模拟仍是研究土拱效应最主要的方法[3]。通过数值模拟方法建立三维隧道开挖模型，结合围岩应力和变形特征，对土拱效应加以分析。本文选用适合模拟非线性岩土工程问题有限差分软件FLAC3D[30]，对隧道开挖过程中的土拱效应进行分析。

2.1 断面选取

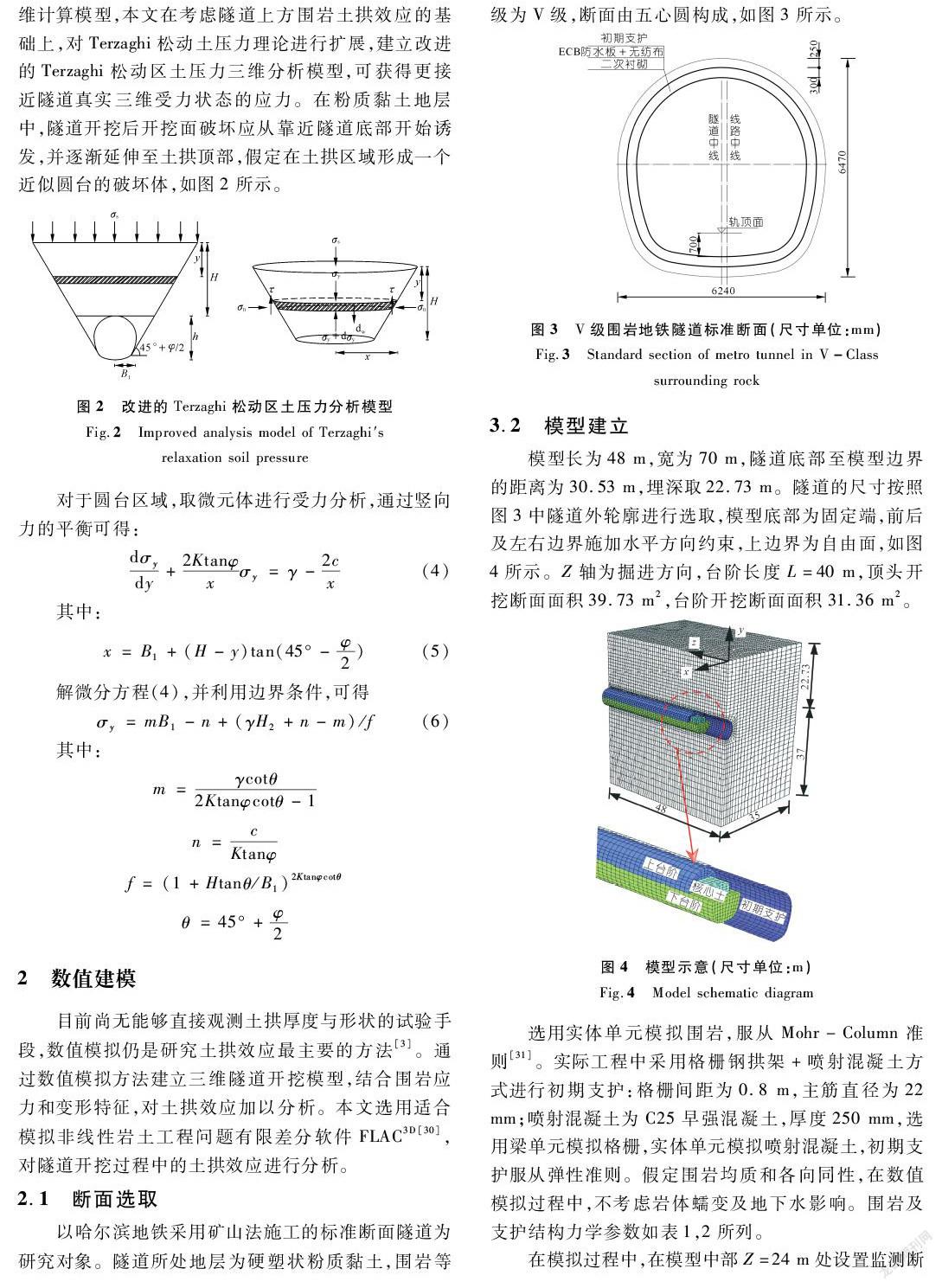
以哈尔滨地铁采用矿山法施工的标准断面隧道为研究对象。隧道所处地层为硬塑状粉质黏土，围岩等级为V级，断面由五心圆构成，如图3所示。

3.2 模型建立

模型长为48 m，宽为70 m，隧道底部至模型边界的距离为30.53 m，埋深取22.73 m。隧道的尺寸按照图3中隧道外轮廓进行选取，模型底部为固定端，前后及左右边界施加水平方向约束，上边界为自由面，如图4所示。Z轴为掘进方向，台阶长度L=40 m，顶头开挖断面面积39.73 m2，台阶开挖断面面积31.36 m2。

选用实体单元模拟围岩，服从Mohr-Column准则[31]。实际工程中采用格栅钢拱架+喷射混凝土方式进行初期支护：格栅间距为0.8 m，主筋直径为22 mm;喷射混凝土为C25早强混凝土，厚度250 mm，选用梁单元模拟格栅，实体单元模拟喷射混凝土，初期支护服从弹性准则。假定围岩均质和各向同性，在数值模拟过程中，不考虑岩体蠕变及地下水影响。围岩及支护结构力学参数如表1，2所列。

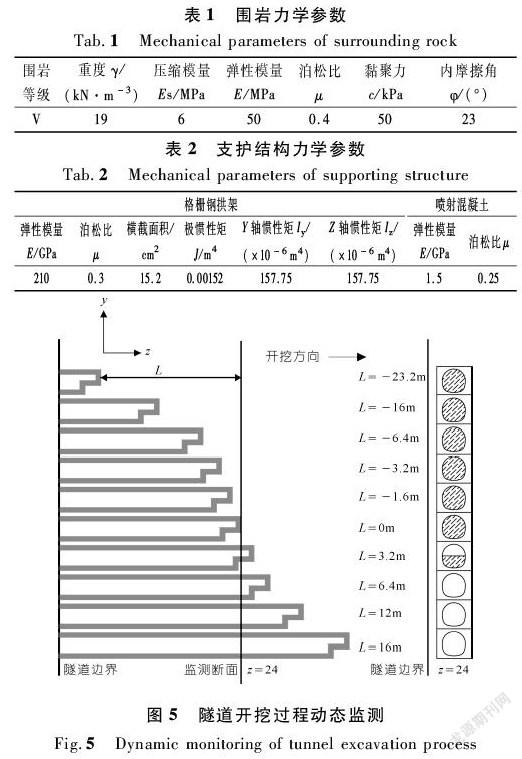
在模拟过程中，在模型中部Z=24 m处设置监测断面（见图5），通过掌子面与监测断面相对距离的变化来反映隧道开挖的时空效应，达到研究土拱效应演化规律的目的。图中L为掌子面距监测断面的相对位置（Z轴正方向为隧道开挖方向，L为负值表示掌子面在监测断面后方，L为正值表示掌子面在监测断面前方）。

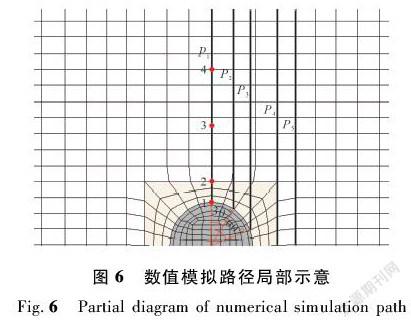
隧道开挖采用上下台阶法预留核心土方式循环开挖，台阶长度为4 m，每次开挖步长为0.8 m，选取10个相对位置进行分析，所对应的L分别为-23.2，-16.0，-6.4，-3.2，-1.6，0，3.2，6.4，12.0，16.0 m。为提取围岩竖向应力和地层沉降，在隧道上部选取5条路径（见图6）。

3 地铁隧道土拱效应演化规律分析

隧道开挖过程中，随着掌子面与监测断面距离的变化，监测断面上围岩应力及地层沉降发生相应改变，对应的土拱分布范围及形态也不尽相同。拱形区域的内外边界通过开挖断面中心线上的主应力-深度关系曲线的拐点确定。

3.1 围岩竖向应力变化规律

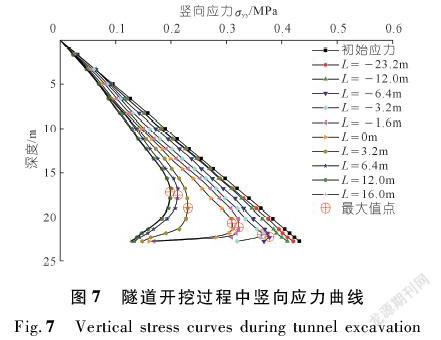
隧道上方P1路径上围岩竖向应力在隧道开挖过程中的变化情况如图7所示。围岩压应力为正。

（1） 当L=-23.2～-12.0 m时，围岩竖向应力由地表至隧道外轮廓呈现线性增加趋势，大小与围岩初始应力基本相同。表明掌子面与监测断面距离大于2倍隧道跨度时，隧道开挖不会造成监测断面处应力重分布;掌子面附近土体未扰动。

（2） 当L=-6.4 m时，竖向应力曲线在隧道拱顶上方约2 m处出现拐点，竖向应力出现最大值，表明掌子面距离监测断面约1倍隧道跨度时，隧道开挖引起监测断面处围岩应力重分布，土拱效应出现，土拱开始形成;曲线开始变为非线性但不显著，表明土拱刚开始发育。

（3） 当L=-3.2～0 m时，竖向应力变化由地表向下呈明显的先增大后减小趋势，竖向应力最大值逐渐减小，竖向应力最大值点出现的高度逐渐增加，表明掌子面距离监测断面1倍隧道跨度以内时，土拱效应对监测断面有显著的影响，土拱高度增加;曲线呈明显的非线性，达到一定深度后应力减小，曲线中带有标记的拐点变得明显

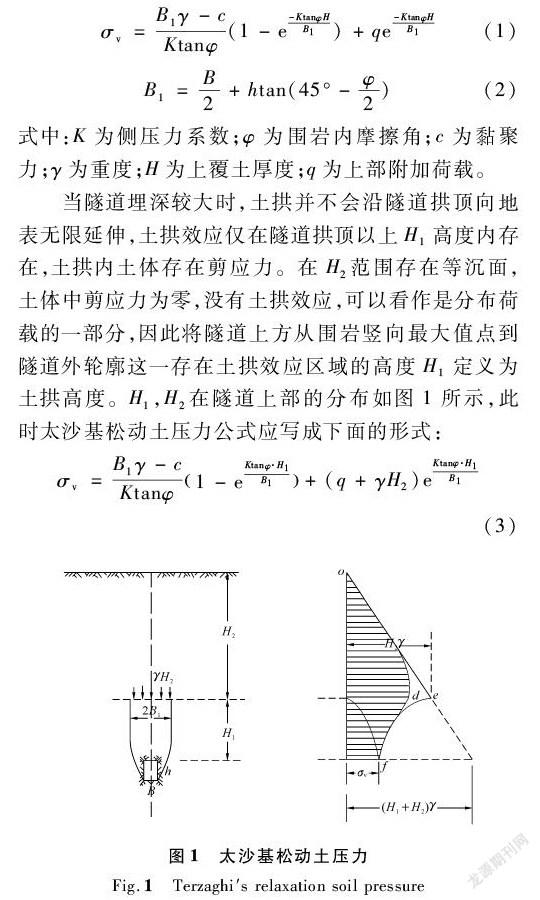
（4） 当L=0～6.4 m时，掌子面通过监测断面，竖向应力大幅减小，土拱高度迅速增加，此阶段土拱发展最为迅速。因为掌子面完全暴露，同时支护结构的设计刚度尚未完全形成，壁后空隙尚未完全填充。当掌子面与监测断面距离大于6.4 m后，竖向应力基本不再变化，土拱稳定。稳定后的竖向应力曲线形态与Terzaghi试验实测曲线odf（见图1）一致，验证了数值模拟分析土拱效应的合理性。

（5） 当远离开挖面约2倍隧道跨度时，从主应力-深度关系曲线发现工作面距离监测站较远，监测断面土体基本未出现扰动，该开挖阶段可能相当于太沙基模拟条件下的平面应变。对比分析隧道开挖全过程中围岩竖向应力曲线的变化规律可以发现，土拱的形成与发展主要集中在掌子面前后1倍隧道跨度范围。

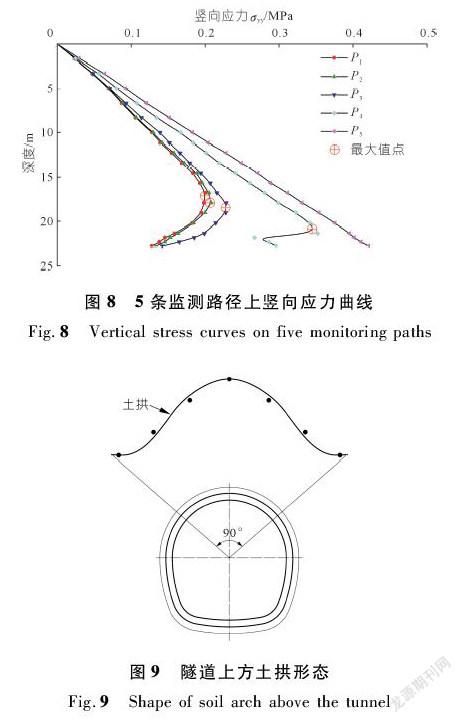
提取土拱穩定后监测断面上P1～P55条路径上围岩竖向应力曲线（见图8）。P1～P4四条路径上围岩应力曲线变化规律基本一致，应力曲线均存在拐点，拐点所对应的高度即为该路径上土拱区域的上边界，P5路径上围岩竖向应力线性增加，与围岩初始应力变化趋势相同，表明土拱效应在隧道横断面上未发展到此区域。将竖向应力曲线拐点所对应的位置相连即可得到隧道上方土拱的形态，如图9所示。

3.2 地层沉降变化规律

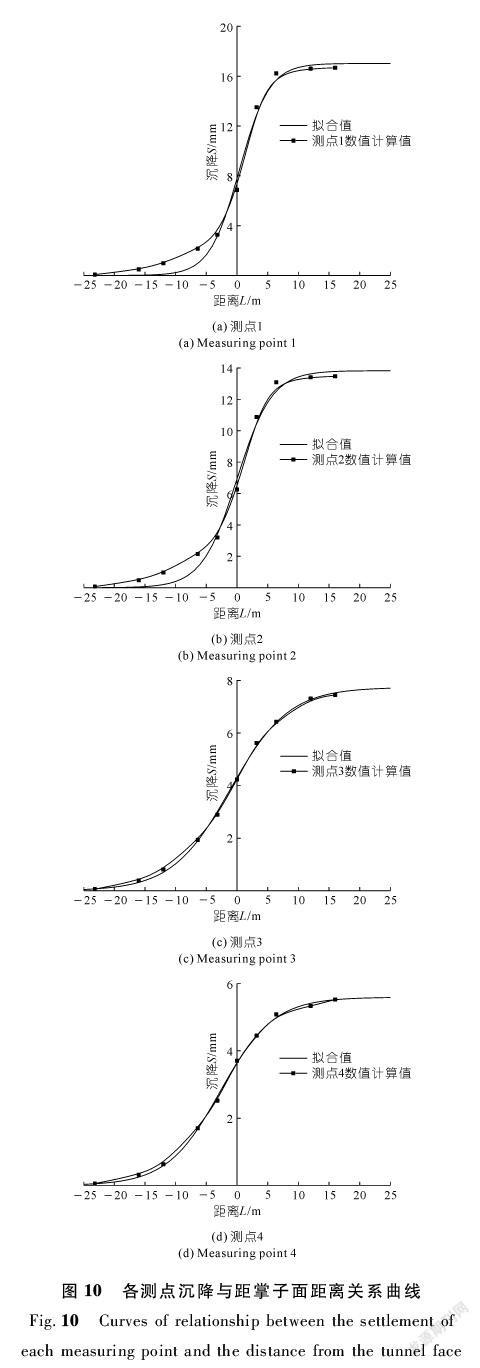
在路径P1上选取1～4号测点，如图6所示，与拱顶的距离分别为0，2，8，14 m，隧道开挖过程中4个测点沉降值与距掌子面距离关系如图10所示。

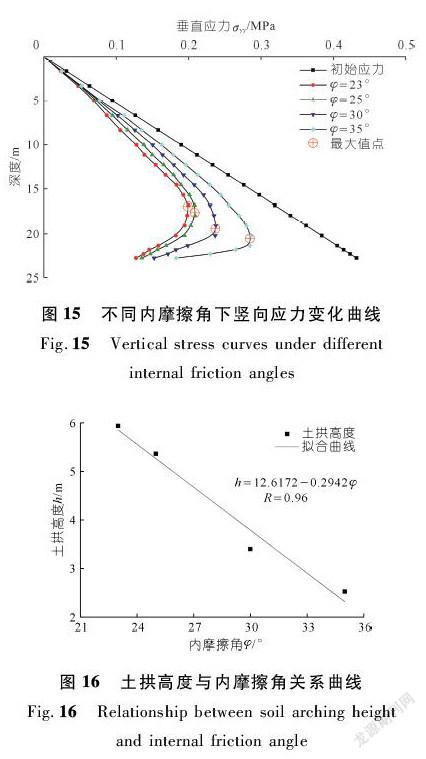
结合图16及式（12）可知：当内摩擦角在23°～35°范围内变化时，土拱高度随内摩擦角增大线性降低。同样地，提取不同黏聚力与内摩擦角组合下路径P1～P5上的围岩竖向应力可得出土拱形态。经研究发现，对该粉质硬塑状粉质黏土来说，在不同组合下土拱变化主要体现在高度上，宽度保持基本不变，土拱主要集中在隧道拱顶90°范围。综合分析可知，土拱形态与围岩参数存在密切联系，围岩性质的好坏对土拱的高度有着显著的影响。实际工程中应当结合围岩性质，针对土拱做出前期预判。对于围岩状况不理想的工况可以采取注浆改良等措施，提高围岩c、φ值以充分发挥利用土拱效应的作用。

6 结 论

（1） 对于深埋软弱围岩隧道而言，隧道开挖后隧道上方形成土拱。土拱内围岩应力及地层沉降变化显著，可根据隧道开挖后隧道上方竖向应力和地层沉降变化曲线对土拱的高度和形状加以判断。

（2） 土拱的形成是一个随隧道开挖逐渐形成的过程，在掌子面前后约1倍隧道跨度范围内土拱效应发展最为显著。对本文的硬塑状粉质黏土地层来说，土拱的范围主要集中在隧道上方90°左右范围，施工应重点对此区域围岩变形加以关注防范。

（3） 综合分析现场监测与数值计算数据可知，土拱效应的存在可以显著减小支护结构受力，同时二者数据的差异较小也验证了数值计算数据的可靠性。

（4） 围岩的力学参数对土拱的形态存在较为明显的影响，随着围岩黏聚力和内摩擦角的增大，土拱高度呈现较为明显的减小趋势;土拱宽度保持基本不变。

参考文献：

[1] 台启民，张顶立，王剑晨，等.软弱破碎围岩高铁隧道压力拱演化规律分析[J].北京交通大学学报，2015，39（6）：62-68.

[2] 白浪峰，徐前卫，田龙岗，等.软弱破碎连拱隧道松动区模型试验与分析[J].岩石力学与工程学报，2013，32（增2）：3610-3618.

[3] CHEN C N，HUANG W，TSENG C.Stress redistribution and ground arch development during tunneling[J].Tunnelling and Underground Space Technology，2011，26（1）：228-235.

[4] 韩同春，邱子义，豆红强.基于颗粒离散元的抗滑桩土拱效应分析[J].中南大学学报（自然科学版），2016，47（8）：2715-2722.

[5] 王俊，林国进，唐协，等.砂土地层盾构隧道稳定性三维离散元研究[J].西南交通大学学报，2018，53（2）：312-321.

[6] 吕玺琳，曾盛，王远鹏，等.饱和圆砾地层盾构隧道开挖面稳定性物理模型试验[J].岩土工程学报，2019，41（增2）：129-132.

[7] 代仲海，胡再强.穿越紧邻隧道时盾构开挖面稳定性分析[J].中国公路学报，2020，33（1）：145-152.

[8] 刘克奇，丁万涛，陈瑞，等.盾构掌子面三维破坏模型构建与极限支护力计算[J].岩土力学，2020，41（7）：1-12.

[9] 白维仕，李荣建，赵学勐，等.基于滑移线网络法的黄土隧道坍塌拱分析及其承载评价[J].防灾减灾工程学报，2020，40（1）：132-138.

[10] 陈强，杨泽平，梁海安，等.基于室内模型试验的砂性土中土拱形态演变的拟合分析[J].科学技术与工程，2018，18（6）：310-315.

[11] 徐超，张兴亚，韩杰，等.加载条件对土拱效应影响的Trapdoor模型试验研究[J].岩土工程学报，2019，41（4）：726-732.

[12] 徐长节，梁禄钜，陈其志，等.考虑松动区内应力分布形式的松动土压力研究[J].岩土力学，2018，39（6）：1927-1934.

[13] 李瑞林，周国庆，林超，等.考虑土拱效应的滑移面间非极限状态土压力解答[J].岩土力学，2017，38（11）：3145-3153.

[14] 娄培杰.考虑土拱效应的浅埋隧道松动土压力计算方法[J].现代隧道技术，2017，54（4）：56-62.

[15] 白廷辉，郑勇波，刘树佳，等.软土深部盾构开挖地层损失率对软土土拱效应的影响分析[J].隧道建设（中英文），2018，38（增2）：1-6.

[16] 陈其志，郭生根，徐长节，等.砂土中松动土压力及松动区位移破坏形式的试验研究[J].中南大学学报（自然科学版），2019，50（1）：108-117.

[17] 陈强，杨泽平，梁海安，等.砂性土中土拱演变阶段及影响因素试验探究[J].公路，2018，12（12）：58-64.

[18] 徐东，周顺华，黄广军，等.上海粘土的成拱能力探讨[J].上海铁道大学学报，1999，20（6）：49-54.

[19] 路德春，曹胜涛，张波，等.隧道开挖围岩土压力拱效应分析[J].地下空间与工程学报，2015，11（6）：1421-1430.

[20] 崔蓬勃，朱永全，刘勇，等.考虑土拱发挥过程的非饱和砂土盾构隧道极限支护力计算方法研究[J].岩土工程学报，2020，42（5）：873-881.

[21] TERZAGHI K.Theoretical soil mechanics[M].New York：Wiley，1943.

[22] NAKAI T，XU L，YAMAZAKI H.3D and 2D model tests and numerical analyses of settlements and earth pressures due to tunnel excavation[J].Soils and Foundations，1997，37（3）：31-41.

[23] LEE C J，WU B R，CHEN H T，et al.Tunnel stability and arching effects during tunneling in soft clayey soil[J].Tunneling and Underground Space Technology，2006，21：119-132.

[24] 喻波，王呼佳.压力拱理论及隧道埋深划分方法研究[M].北京：中国铁道出版社，2008.

[25] 郑颖人，徐浩，王成，等.隧洞破坏机理及深浅埋分界标准[J].浙江大学学报（工学版），2010，44（10）：1851-1856.

[26] CHAPPELL B A.Deformational Response in discontinua[J].International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts，1979，16（6）：377-390.

[27] LIN X，LIU Y，KANG X，et al.Numerical simulation on the development of soil arching Induced by EPBS tunnelling[M]∥ Proceedings of the 2nd International Symposium on Asia Urban GeoEngineering.Hangzhou：Zhejiang University Press 2018：575-582.

[28] 孙潇昊，缪林昌，林海山.不同埋深盾构隧道开挖面稳定问题数值模拟[J].东南大学学报（自然科学版），2017，47（1）：164-169.

[29] 谢家杰.浅埋隧道的地层压力[J].土木工程学报，1964，6（7）：58-70.

[30] 台启民，张顶立，房倩，等.暗挖重叠地铁隧道地表变形特性分析[J].岩石力学与工程学报，2014，33（12）：2472-2480.

[31] PARDO G S，SEZ E.Experimental and numerical study of arching soil effect in coarse sand[J].Computers & Geotechnics，2014，57（4）：75-84.

[32] 乔丽苹，刘杰，李术才，等.地下工程开挖面空间效应特征研究及应用[J].岩土力学，2014，35（增2）：481-487.

[33] 张瑞.地铁区间隧道围岩压力机理研究[D].石家莊：石家庄铁道大学，2013：38-46.

（编辑：郑 毅）