键合丝产品开发中物理原理探究

任智

（百色学院材料科学与工程学院物理系 广西壮族自治区百色市 533000）

2020年9月22日，中国宣布碳中和目标，碳中和与泛高端制造已然成为中国实体经济发展的两个主赛道，有关节能、绿色能源方面的行业会获得井喷似的发展。IGBT 是功率半导体中最重要的元件之一[1]，其可靠性研究是目前的热点领域,粗铝线从铝芯片金属层的脱落是主要失效模式[2]。在弱电领域，键合金线由于成本和高温可靠性问题，逐渐被1wt%含钯金线所替代（Au-1wt.% Pd wire），主要原因之一是后者高温可靠性的提升。目前粗铝线主要采用向5N8纯度的高纯铝中加入5-20 ppm 的高纯Si 和40-60 ppm 的高纯 Ni（4N），但为何要加入这5-20 ppm 的硅，技术文献中并未真正说明。现在国内线材公司处于仿制阶段，而研究单位对于粗铝线的研究偏少，合金配方机理的研究完全空白，急需国家的高校和研究单位对配方中各个元素所具有的“功能性”做出判断。行业对于自主创新的需求很强烈，而自主创新就必须针对配方设计背后的物理机制进行深入系统的研究。

1 键合丝焊点高温可靠性失效物理机制，原子的空位（vacancy）扩散机理

图1(a)显示了含钯金线球焊在芯片铝金属层后在高温下老化500 小时后的剖面图[3]，可见焊点是完整的，没有出现纯金线那样的严重的柯肯达尔空洞，如图1(b)[4]，说明柯肯达尔效应被有效地抑制了。这主要是金原子向铝层的扩散速度要远远大于铝原子向金线扩散的速度（空位的扩散方向则相反）。而要维持金原子向铝层的高速扩散，金原子在其线材内部向界面的扩散速度是决定步骤，因为如果线材内部的金原子不能保持供应，金原子向铝层的扩散就不能持续；另外正是金原子向金铝界面的扩散，导致了柯肯达尔空洞在界面附件靠金层方向上形成，最终影响了线材的高温可靠性。

图1

1.1 原子自发扩散的空位机理（vacancy mechanism）

晶体中原子的扩散现象可以分别由图2 和式（1）来描述[5]。

上式中的J 表示扩散通量，显然由于线材内部由于各处的金原子浓度相同，J=0，只有在界面附件存在浓度梯度的地方,才有宏观可见的扩散现象，在金晶体内部金原子向各个方向的扩散速度是相同的。进一步考察扩散的微观机理发现，金原子在晶体内部进行着不停的跃迁，从原始位置采用图2 中的机理转移到附近空位的位置。相应的数学描述为：

其中的г 为跃迁频率。从图2 下部的能量构型可知，金原子在原始平衡位置时所对应的能量是最低的，当它由于热运动碰撞获得了足够的能量（热能量会传递到该原子的每个电子和原子核）而试图通过中间的构型时，此中间构型是能量最大的构型，原子间的距离也由原来的a 变成了a’。显然有下式：

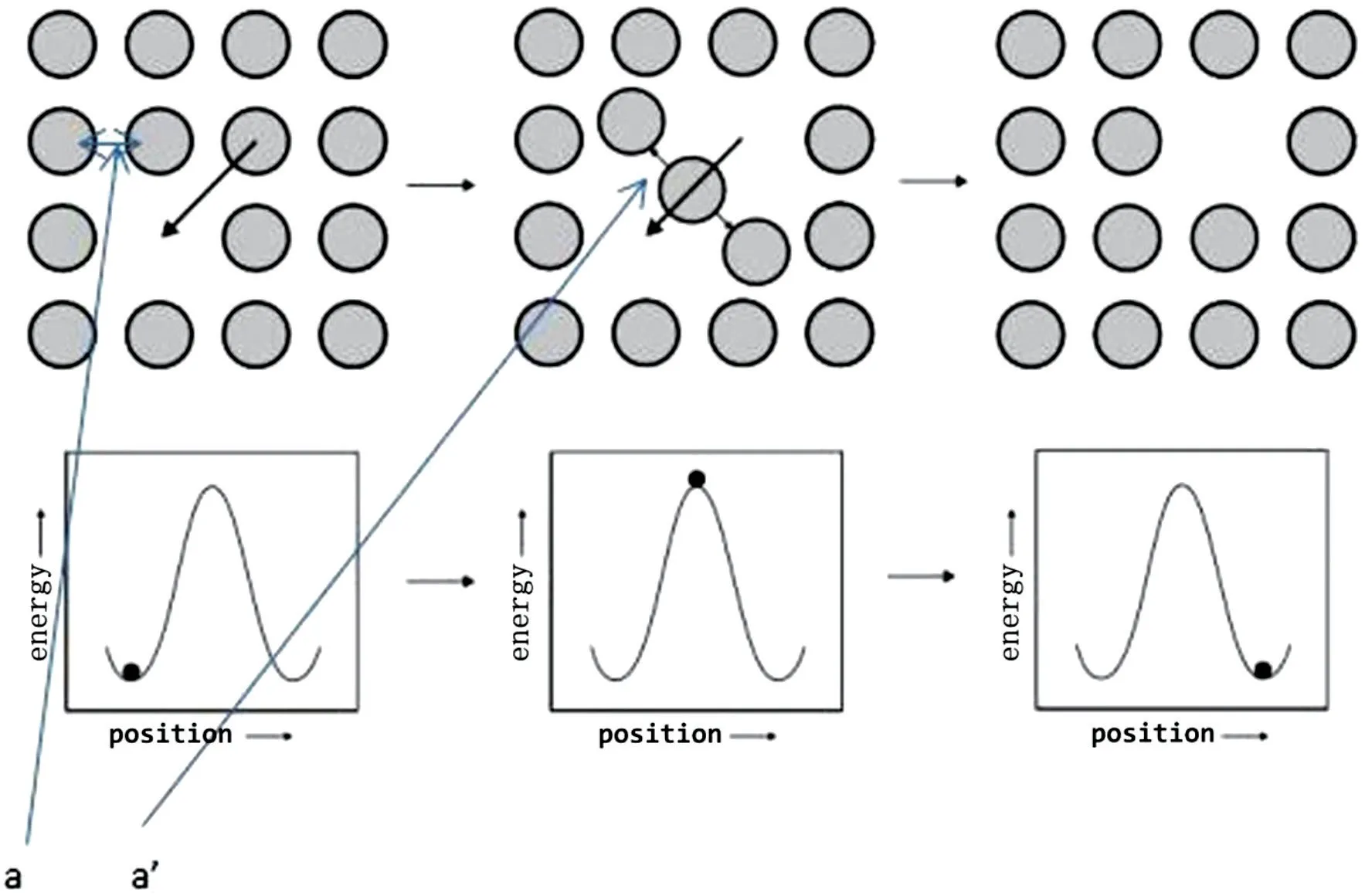
图2：原子扩散的空位机理（Vacancy mechanism）

上式表明，跃迁频率与活化能Ea相关，Ea越大则，跃迁频率越小。在相同的浓度梯度下，原子的扩散速度会越小，对抑制柯肯达尔效应有利。下面采用量子力学的原理来解释这个扩散活化能的问题。

1.2 自扩散活化能的量子力学解释

1.2.1 周期场中的电子，能带理论

晶体中的原子排列是有结构的，为简化起见，通常先分析一维的情况再扩展到三维。如图3所示周期排列的原子核所形成的势能场[6]。

通过对实际电子势能周期场的简化，可以对图3(b)所示的I,II 区（a,b 分别为此两区的宽度）分别列出薛定谔方程，并根据周期性边界条件和对II 区域势能曲线的进一步简化（在保持b*V0为常数的情况下，假定b →0,V0→∞），求得解（电子特征波函数）要满足下式：

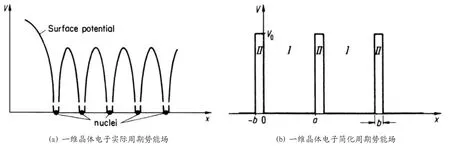
图3：周期排列的原子核所形成的势能场

其中：

m,E 分别是电子的质量和能量，将式4 右边的函数做图如下，由于等式的右边表明方程有解时，等式的左边的取值要在-1 和1 之间。如图4所示。

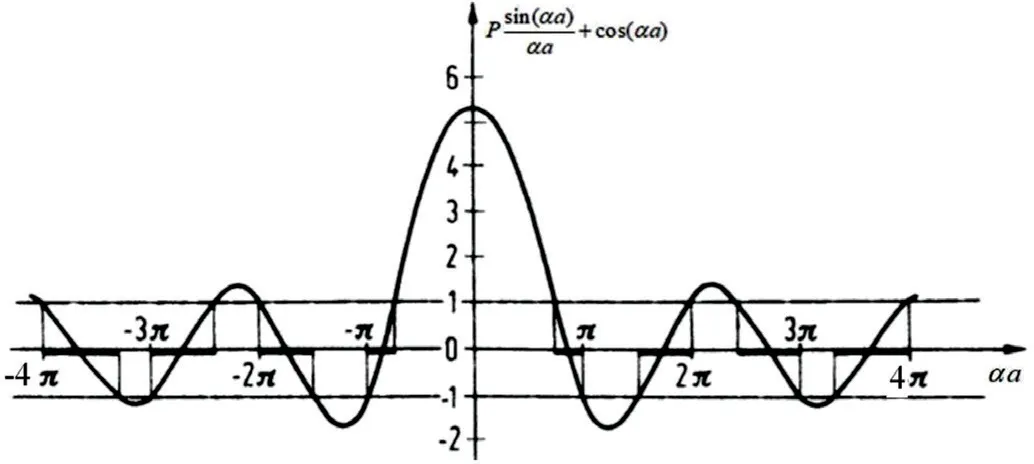
图4：周期场的电子波函数所体现出的波数K 取值的区域不连续性（能带）

显然电子可以取值的区域是图4 横坐标上粗线条所代表的区域，能级的概念因此出现。当其它参数不变仅仅改变原子间距离时，电子结构出现了由单个能级向能带的变化，如图5。

图5：随原子间距离的增加，能带的宽度不断增加

做为一种近似描述，当金原子自扩散通过最高能量构型时，原子间的距离从a 降低到了a’,所以原来的能带会变得更宽，在此对于金原子来讲，6s 能带会变得更宽。

1.2.2 金和钯晶体的态密度（能级密度）

在一个能带中单位能量间隔内所包含的能级数目被称为态密度，对于晶体这样复杂的多粒子量子体系，通常我们假定原子核固定在平衡位置来求取相应的电子波函数，因此求得的波函数对应于晶体在绝对零度下的基态，主要有两大类方法：

（1）基于电子密度的密度泛函法；

（2）基于单电子近似的方法。

图6所示的态密度就是利用单电子近似理论中的缀加平面波法数值（augmented plane-wave method）求取得到的金和钯晶体的态密度分布图[7]。

图6：晶体的态密度图

图中的虚线是Fermi 能级所在的位置，显然Au 晶体费米能级之上6s 能带上的态密度是比较大的，而钯晶体费米能级之上的5S 能带上的态密度几乎为零。

综合上面两方面的资讯不难推导出以下结论，当温度升高时，热运动使得各原子的能量通过热碰撞相互转移交换，某时刻某原子可能通过热碰撞获得较大的能量而振动到图2中间所示的高能量构型位置，这时原子的能量是分布到该原子的每一个组成微粒的，尤其是价电子能量得到激发，上升到Fermi 能级之上。对于金晶体这样的物质而言，原子间的这种构象导致相邻原子间距离从a 降到a’，6S 能带（Fermi能级在其中）变宽，另外金原子Fermi 能级之上态密度较大，存在充裕的空能级提供给受到激发的高能电子，所以价电子在这个区域（或方向）出现的概率比其它方向更高。电子在此的富集意味着能很好地屏蔽相互靠近的原子核（或是离子实）之间的库伦排斥力，发挥量子胶水的作用，进而降低这个构型所对应的式3 中的活化能Ea。钯晶体的情况恰恰与此相反，所以前者比后者有更大的自扩散系数，柯肯达尔效应显著。因此可以预见当讲1wt%的钯加入到金晶体中时，由于两者完全固溶，所以这个合金的电子结构会向钯的电子结构偏移，金原子在合金晶体中自扩散时，电子富集效应降低，活化能升高，所以跃迁频率下降，柯肯达尔效应受到抑制。相应的合金焊点的高温可靠性性能得到提升。

2 CTE的量子力学解释与IGBT粗铝线失效模式探究

2.1 CTE量子力学分析

固体物理考察晶体时认为原子核因热运动在平衡位置振动[8]，晶体内所有电子和原子核所构成的量子体系的宏观波函数可以表达为下式：

ri，Rl分别为每个电子和原子核的位置，t 为时间。体系的哈密尔顿量为：

Zl为在Rl位置原子核的原子数，第3，5 项加和符号右上端的标号表示忽略i=j 和l=l’项。上面的式还可以进一步简化为：

其中U 代表了所有的势能项，TE和TN分别代表电子和原子核的动能：

由于电子的质量远远低于原子核的质量（质子的静止质量是电子的1835 倍），所以可以认为电子运动速度远远高于原子核。也即上式的HL相应于H0很小，这样实际体系的哈密尔顿量可以看成在H0（原子核保持静止在Rl位置时的物理体系）上的微扰。

实际体系的定时薛定谔方程为：

假定原子核固定在Rl位置时，体系电子的定时薛定谔方程为：

在H0所代表的体系基础上，实际体系与之的差别体现在两个方面：

（1）原子核离开平衡位置（在微扰法求解时，原子核的任意位置Rl被重新定义为其离开平衡位置的量来表达，也就是H0的状态在微扰理论处理的过程中被选择到了原子核的平衡位置）；

（2）原子核的动能不为零。这样微扰理论下，体系的波函数可以写成：

如果上述波函数可以只近似取到K2项，则体系的波函数可以写成原子核和电子波函数相乘的形式[9]：

上式中的χ 表示原子核的波函数，此式就是波恩–欧本海默近似(Born-Oppenheimer approximation)的数学表达式，物理上的意义就是指：当原子核的质量远大于电子质量时，电子的运动速度远大于原子核，所以可以假定原子核在运动过程中的每一个位置，电子都有足够的时间建立以此原子核的构型相对应的平衡稳定电子构型，也即电子的运动和原子核的运动是解耦的。对于金属晶体来讲，这个假定是会导致误差的，因为金属电阻的存在就表明电子运动和原子核运动是关联的。在波恩–欧本海默近似的基础上，原子核间的有效势能可以表达为原子核离开其平衡位置位移的四次方及以下次幂。原子核间的有效势能的表达式中那些原子核离开平衡位置的项的次幂高于2 次方项，小于等于4 次方项的，被称为非谐项（anharmonic terms），它们表征了晶体内部原子热振动（声子 phonon）之间的相互作用所导致的热膨胀现象。对于硅，氧化铝这些晶体，波恩–欧本海默近似是成立的，所以这类晶体的CTE 比较小，主要源于非谐项的贡献，而对于金属晶体，除了非谐项的贡献，原子核运动和电子之间的耦合关系也是导致CTE 的主要原因。

2.2 IGBT键合丝失效的原因分析

图7(a)是IGBT 封装示意图，铝和硅的CTE 分别为23（µm/(m·K)）和4（µm/(m·K)），图7(b)是IGBT 封装失效时，在粗铝线材与芯片铝金属层间界面的上部，键合丝内部出现的裂缝电镜图。显然该裂缝起源于焊线和芯片铝金属层的界面上。为了增加抗电迁移能力，芯片的铝金属层通常是在5N5 的纯Al 中加入1wt%的Si 和0.5wt%的Cu 来制造的。

图7：IGBT 封装

现有的提高IGBT 的功率循环可靠性的封装解决方案包括日本田中方案(通过在粗铝线中加入0.8wt%的铁来增加粗铝线的机械强度)和贺利氏的铜线方案。现有的文献对失效现象的描述和封装改进方案的实验比较多，但是对最微观层面上，微裂缝的产生机理研究不多。本文认为，根据量子力学的热膨胀解释中的微观图像，热应力所导致的微裂缝除了应该出现在芯片Si 层和芯片铝金属层之间外，对于粗铝线脱落的可靠性失效模式，还应该考虑楔形焊接过程中那些从粗铝线表面和芯片铝金属层表面脱离下来的氧化铝碎片（CTE 为8.1µm/(m·K)）[10]，它们并没有完全被清除出粗铝线和铝金属层焊接界面，它们在界面的存在应该是造成粗铝线中产生裂缝和脱落的主要研究对象和可能的原因。

3 硅铝固溶度与可靠性

上已述及IGBT 铝金属层中加入1wt%的硅和0.5wt%Cu可以抑制电迁移，同时1wt%Si 还可以防止硅从芯片向铝金属层扩散。若粗铝线为纯铝，器件在工作时，IGBT 芯片表面温度可达423K（150℃），从表1文献数据[11]可知此温度下，硅在铝中的固溶率为17.8ppm，此时芯片表面的Si 和铝金属层中的硅会向粗铝线中扩散，会导致铝金属层中空位或空隙形成，危及可靠性。

表1：不同温度下硅在铝中的固溶度

4 结论

本文研究了键合丝电子封装中与可靠性相关的三个实际问题，从底层物理机制方面剖析了合金配方和工艺过程对封装可靠性的影响，为后续的产品开发和封装工艺改良提供了新思路。