动力系统的Poisson结构和可积变形
2022-03-31张亚欣黄晴
张亚欣,黄晴
(西北大学数学学院,陕西 西安 710127)
1 引言
Hamilton系统是非线性科学研究中的一个重要领域,广泛存在于数理科学,生命科学和社会科学中.经典力学的Hamilton理论是定义在偶数维相空间上的,如果一个自由度为n的Hamilton系统H有包含H在内的n个泛函独立且两两对合的守恒积分,则称系统H在刘维尔意义下是完全可积的[1-2].此外,如果完全可积系统H还存在仅与H对合且相互独立的m个守恒积分,m满足n 目前对给定可积系统进行可积变形的研究已有一些结果,文献[11]基于具有斜积映射的Poisson代数构造了一类三维Lotka-Volterra方程的可积变形.文献[12]基于相容Poisson结构族的构造得到了Bogoyavlenskij-Itoh系统的可积变形族.文献[13]通过推广守恒积分构造了Euler陀螺的可积变形.文献[14]将Poisson-Lie群作为Lie-Poisson代数的变形,给出了某些可积型Rössler和Lorenz系统的可积变形.文献[15]给出了最大超可积系统的可积变形方法. 本文以保守Lorenz系统为例,构造该系统的Poisson结构,通过添加任意可微函数推广守恒积分,利用这些新的函数构造一个新的系统,称为原来系统的可积变形,并给出变形后系统的Poisson结构. 定义 2.1[5]光滑流形M上的广义Poisson括号是定义在光滑函数空间C∞(M)上的一个运算{·,·},对于任意的函数F,G,K∈C∞(M),该运算满足如下四条性质: (i)双线性:{aF+bG,K}=a{F,K}+b{G,K}; (ii)反对称性:{F,G}=−{G,F}; (iii)Leibnitz 法则:{F·G,K}=F·{G,K}+G·{F,K}; (iv)Jacobi恒等式:{F,{G,K}}+{G,{K,F}}+{K,{F,G}}=0. 具有广义 Poisson括号结构的流形M,称为 Poisson流形,记作 (M,{·,·}).在定义2.1中,没有限定M的维数,M可以是任意有限维或无穷维流形,特别地可以是奇数维流形,并将广义Poisson括号简称为Poisson括号.设Poisson流形的局部坐标为 (x1,x2,···,xn),其结构矩阵P(x)的元素由Pij(x)={xi,xj}定义,并有如下命题. 命题 2.1[5]对于任意一个函数矩阵P(x)=(Pij(x))(x=(x1,x2,···,xn)),该矩阵是一个Poisson括号的结构矩阵的充要条件是: 由结构矩阵P(x)可定义任意两个函数F,G的Poisson括号 设系统的Hamilton函数为H(x),则系统的运动方程可表示为Hamilton形式 称如上系统为广义Hamilton系统. 经验证{Fi,Fj}=0,i,j=1,2,···,n−1,因此广义Hamilton系统 (3)是刘维尔完全可积系统. 当αβ时,Pα∇Fβ=0,α,β=1,2,···,n−1.在(3)式中可以取F1,F2,···,Fn-1中的任意一个函数作为Hamilton量,其余的记作该Hamilton系统的Casimir函数,因此Rn中的所有自治动力系统(1)都是广义Hamilton系统,其形式如(3)式所示,并且用这种方式构造的结构矩阵的秩为2. Lorenz系统由如下方程给出 其中σ,ρ,β是实参数.这里考虑系统(4)的保守极限,由如下的伸缩得到 取极限ρ→∞.在该变换下,系统(4)为 易得系统(5)的两个守恒积分 选取F1作为Hamilton量,F2作为Casimir函数,则系统(5)的广义Hamilton形式为计算得 同样地选取F2作为Hamilton量,F1作为Casimir函数,得到其结构矩阵为 因为P1+P2是一个结构矩阵,所以 Poisson括号{·,·}1和{·,·}2是相容的,系统 (5)有如下形式=P1∇F1=P2∇F2,由此系统(5)是bi-Hamilton系统. 如果一个动力系统的时间变量重新参数化,其守恒积分仍唯一地确定系统本身,那么可以利用这一性质构造它的可积变形.对上述守恒积分求导得 根据这一性质,通过添加两个任意的可微函数g1(x1,x2,x3),g2(x1,x2,x3)推广守恒积分(6) (7)式关于时间变量求导得 解方程组(8)得到系统(5)的可积变形 如果g1,g2是常值函数,那么系统(9)退化为初始系统(5).易证(7)式是系统(9)的守恒积分. 下面构造系统(9)的Poisson结构.令H:=1,对应的结构矩阵1满足 从而通过可积变形得到的刘维尔可积系统(9)可表示为广义Hamilton系统. 本文研究了保守 Lorenz系统的 Poisson结构和可积变形.利用守恒积分构造Poisson结构,将动力系统表示为广义Hamilton系统的形式,从而证明了动力系统的完全可积性.通过推广守恒积分构造系统的可积变形,得到了新的刘维尔可积系统.2 广义Hamilton系统
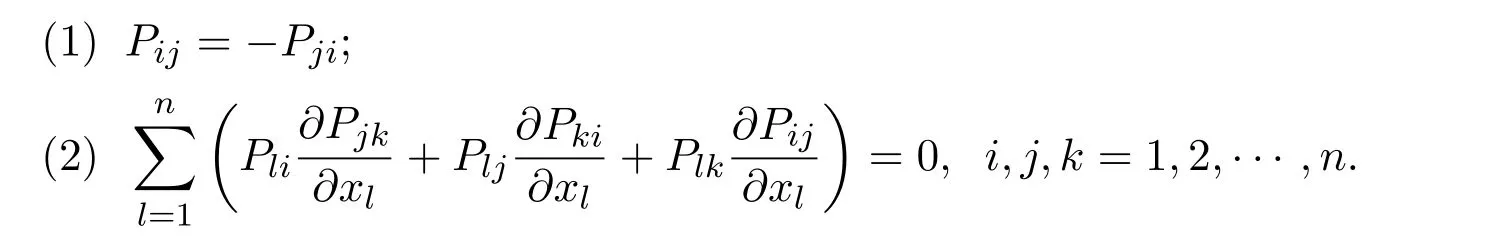


3 动力系统的Poisson结构


4 保守Lorenz系统的可积变形
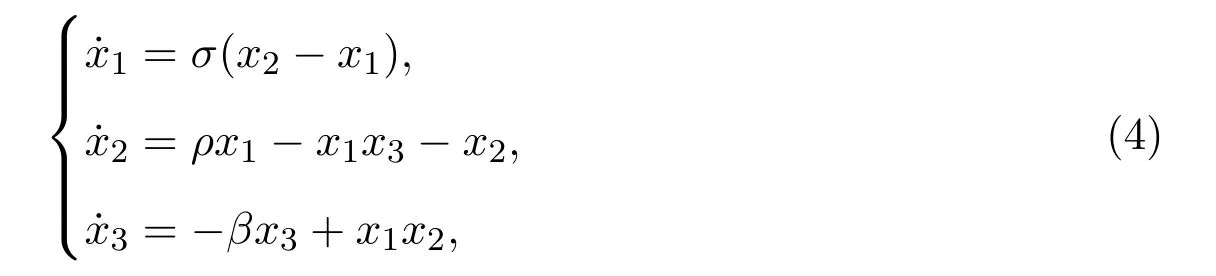
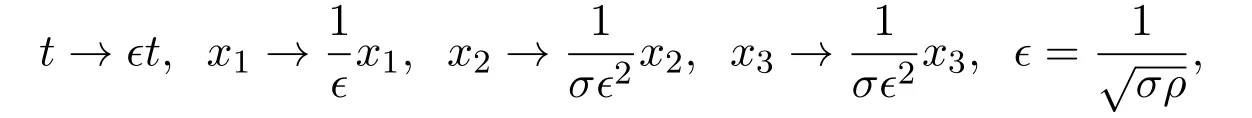

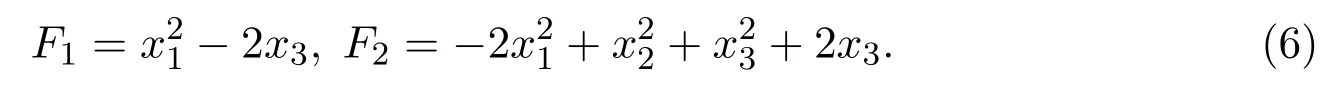
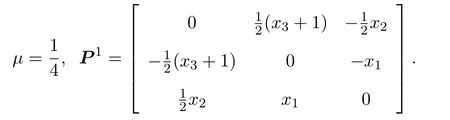
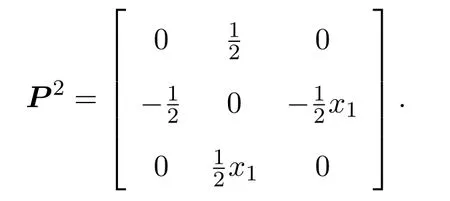

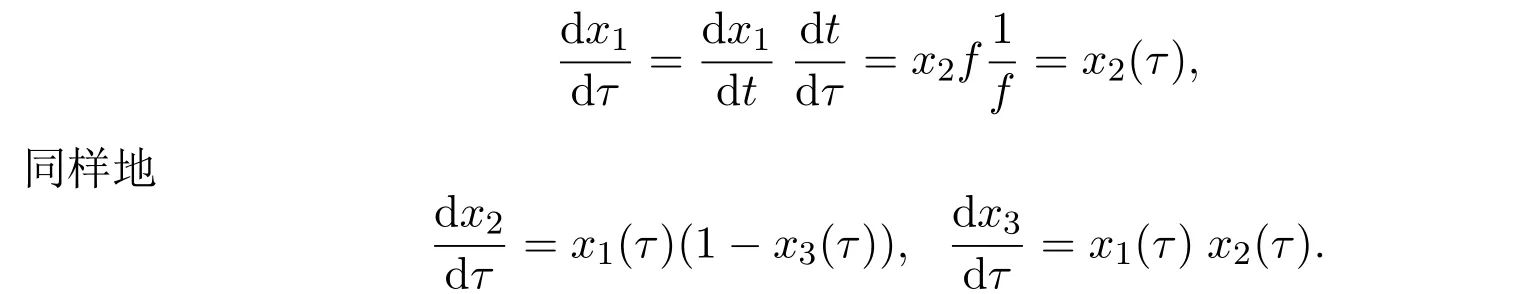
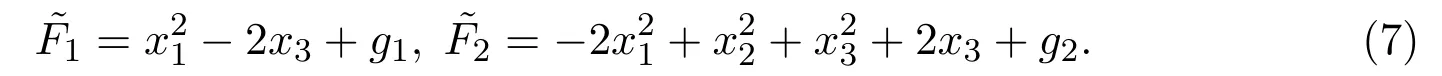

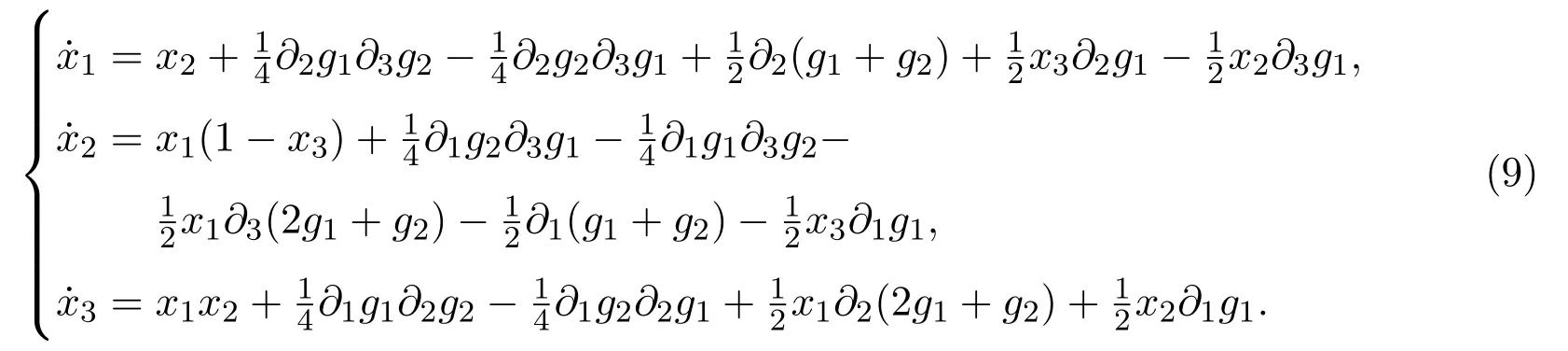

5 总结
