可换逻辑的代数语义综述
2022-03-31杨小飞辛小龙
杨小飞, 辛小龙
(1.西安外事学院商学院,陕西 西安 710077;2.西北大学数学学院,陕西 西安 710127)
1 引言
经典逻辑的代数语义是布尔代数,布尔代数是由 Boole于 1847年在其著作《Mathematical Analysis of Logic》提出的一种代数系统.布尔代数是有补的有界分配格,格的交运算对应为逻辑的合取,格的并运算对应为逻辑的析取,格的补运算对应为逻辑的否.在本文中,为了将布尔代数直接解释为经典逻辑,给出了布尔代数中元素真假的判定方法,从而布尔代数中的元素可以看成命题,布尔代数中的交、并和补分别是逻辑的合取、析取和否,即布尔代数是经典逻辑.在布尔代数中,两个重要的等式是x∨x′=1和x∧x′=0,这里x′表示x的补元.从中可以看出,原命题及其否命题有且只有一个为真,这是恒真命题.
从经典逻辑到模糊逻辑,重要的突破是两个重要的等式不必成立,即在模糊逻辑中,x∨x′=1和x∧x′=0一般不成立.这就导致了真值域由{0,1}扩大到更多元素的集合,从而出现了更加复杂的逻辑语构系统以及相应的代数系统.这些常见的代数系统有MV-代数[1],BL-代数[2],MTL-代数[3],剩余格[4]和半-Hoop[5].为了给出ukasiewicz Logic的代数语义,文献[1]定义了MV-代数,文献[6]给出了完备性证明.为了对连续t-模诱导的模糊逻辑公理化,文献[2]提出了BL逻辑(Basic Logic),该逻辑的代数语义是BL-代数.进一步,为了对左连续t-模诱导的模糊逻辑公理化,文献[3]提出了MTL逻辑 (Monoidal t-norm based Logic),其代数语义是MTL-代数.剩余格是环上理想格的一般化[4],是子结构逻辑[7]的代数语义.由于这些代数系统剩余性(乘法与蕴含是伴随)都是成立的,因此不妨把他们称为剩余结构.由于这些剩余结构不涉及谓词的量化,通常被认为低阶模糊逻辑的语义系统.进一步,本文将介绍高阶模糊逻辑的语义系统,主要介绍两类代数系统:EQ-代数[8]和相等代数[9].
本文主要介绍经典逻辑和模糊逻辑对应的代数结构,借助例子讨论他们之间的关系,进而给出了这些代数结构在概率、格序群和拓扑中的研究进展,最后给出一些公开问题.本文对这些逻辑代数给出了看法,例如通过极大滤子判定布尔代数元素的真假,从而得到布尔代数是经典逻辑;从代数的观点给出模糊逻辑与经典逻辑的区别.希望初学者能对可换逻辑代数有一个初步的了解,进而找到感兴趣的方向.
2 经典逻辑与布尔代数
经典逻辑的代数语义是布尔代数,布尔代数是有补分配格.具体定义如下:
定义 2.1[10]设B是一个集合.称(B,∨,∧,′,0,1)是布尔代数,如果它满足
(B1)(B,∨,∧,0,1)是有界分配格;
(B2)对任意的x∈B,存在唯一的x′满足x∨x′=1和x∧x′=0.
为了说明布尔代数是经典逻辑,下面介绍滤子及性质.具体如下:
定义2.2[10]设L是格,∅F⊆L.称F是格L上的滤子,如果对任意的x,y∈B满足(F1)若x∈F且x≤y,则y∈F;(F2)若x,y∈F,则x∧y∈F.
下面给出布尔代数上极大滤子的刻画,记布尔代数B上全体极大滤子为F(B).
命题2.1[10]设B是布尔代数,F是B上的滤子,则下列条件等价:
(1)F是极大的;(2)F是素的;(3)∀x∈B满足x∈F当且仅当x′F.
对偶地,可以得到格上理想的定义及布尔代数上极大理想的相应性质.
给定一个布尔代数,如何说明它是经典逻辑?关键是如何判断布尔代数中元素的真假.在经典逻辑中一个命题是真或者是假,且只能占其一.由此把问题转化为如何把布尔代数划分为两类的问题,下面给出方法.任给布尔代数B,任给B上的极大滤子F.令F′={x′|x∈F},由F是布尔代数上的极大滤子和命题2.1可以验证F′=Fc,这里Fc表示F的补集,进而由文献[10]中的定理9.8可知F′是极大理想.由此得到B上的划分{F,F′},它具有性质:F是极大滤子且F′是极大理想.因此可以把F中的元素理解为真命题,F′中的元素理解为假命题.通过下面的定理可知布尔代数及其一个极大滤子是经典逻辑.
定义 2.3[11]设B是布尔代数,称e:B−→{0,1}是赋值映射,如果e满足
(E1)对任意的x∈B,e(x)=1−e(x′);
(E2)对任意的x,y∈B,e(x→y)=0当且仅当e(x)=1,e(y)=0,这里

记布尔代数B上的全体赋值映射为Ω(B).由文献[11]引理1.2.18知赋值映射保∧,∨运算.
定理 2.1设B布尔代数,则F(B)与Ω(B)存在双射.
证明给定F∈F(B),定义eF:B−→{0,1}具体为eF(x)=1,x∈F,否则eF(x)=0.下面证明eF是赋值映射,从而eF∈Ω(B).首先证明eF满足(E1),对任意的x∈B,由F是极大滤子知x∈F当且仅当x′/∈F,从而eF(x)=1当且仅当eF(x′)=0.这就证明了eF(x)=1−eF(x′).下面证明eF满足 (E2),设eF(x→y)=0,由x→y=x′∨y知x′∨y∈Fc.因为Fc=F′是理想,所以x′∈Fc,y∈Fc.由Fc={x′|x∈F}知x∈F,这就证明了eF(x)=1,eF(y)=0.另一方面,设eF(x)=1,eF(y)=0,则x∈F,由F是极大滤子知x′∈Fc.由Fc是理想知x′∨y∈Fc,即eF(x→y)=0.
给定e∈Ω(B),定义Fe={x|e(x)=1},下面证明Fe是极大滤子,从而Fe∈F(B).首先证明Fe保上集,设x∈Fe且x≤y,则1=e(x)=e(x∧y)=e(x)∧e(y).从而e(y)=1,即y∈Fe.其次x,y∈Fe,则e(x∧y)=e(x)∧e(y)=1,即x∧y∈Fe.由e满足(E1)知对任意的x∈B有e(x)e(x′),这说明对任意的x∈B有x∈Fe当且仅当x′/∈Fe.由命题2.1知Fe是极大滤子.
容易验证FeF=F和eFe=e成立,从而F(B)与Ω(B)存在双射.
定理2.1说明极大滤子是赋值映射的刻画.当给定布尔代数的一个极大滤子时,布尔代数是一个经典逻辑.需要注意的是,在给定的布尔代数上,当选择不同极大滤子时,会对应不同的逻辑系统.直观的理解,极大滤子是判断布尔代数中元素真假的标准.在不同的标准下,布尔代数中元素的真假会不同.后文中,涉及“标准”特指极大滤子.
例2.1设B={0,a,b,1},其上序为0≤a≤1和0≤b≤1.令F1={a,1},F2={b,1},则Fi是极大滤子,i∈{1,2}.a在标准F1下为真,在标准F2下为假.在这个意义下,布尔代数B上有两个逻辑系统.
命题2.2设B是布尔代数,则∩F(B)={1}.
证明设 1b∈B,则 [b′,1]:={x∈B|b′≤x≤1}是真滤子,从而存在极大滤子F包含[b′,1].由B是布尔代数可知bF,因为F是真滤子.这说明∩F(B)={1}.
设B是布尔代数,且b∈B−{0,1}.命题2.2说明一定存在一个标准(极大滤子)使得b是真的,同时也存在另一个标准使得b是假的.命题2.2也说明只有元素1在所有标准下是真的.这说明所有极大滤子的交有着明显的逻辑意义,即所有极大滤子的交是恒真命题.对偶地,所有极大理想的交是恒假命题,所有极大理想的交是根理想的定义,因此根理想的逻辑意义是恒假命题.
下面用布尔代数是经典逻辑的结论,给出有限布尔代数表示定理中n的确定方法.
命题2.3[10]设B是有限布尔代数,则B同构于幂集格2n.
如何找到命题2.3中的n呢?下面从逻辑的角度理解布尔代数,并给出答案.给定集合A={a,b,c},则得到布尔代数(B,⊂),这里

当把布尔代数B看作是经典逻辑系统时,则{a},{b},{c}是原子公式.从格的视角看待这个问题,{a},{b},{c}覆盖了最小元,因此称这些元素为原子[6].这就可以看做格中原子概念的由来.进一步,记A(B)是布尔代数B的所有原子,从这些原子公式出发,通过合取、析取和否运算可得到逻辑系统的所有公式构成的集合B,即从逻辑的角度看下面的命题是显然的.
命题2.4[10]设B是有限布尔代数,则B同构于幂集格2|A(B)|.
3 模糊逻辑与剩余结构
基于t-模的逻辑系统是模糊逻辑中重要的一类,t-模可以解释为两个命题之间的合取.当t-模是左连续时,它可以诱导剩余性蕴含,从而可以利用t-模表示蕴含算子和伪补算子(¬x=x→0,这里0是最小元).因此,这一节围绕由合取算子⊙和剩余性蕴含算子→构成的剩余结构讨论这些代数系统.半-Hoop是一类较为宽泛的剩余结构,下面给出它的定义.
定义 3.1[5]称 (L,∧,⊙,→,1)是半 -Hoop,如果它满足
(SH1)(L,∧,1)是∧-半格且1是最大元;(SH2)(L,⊙,1)可换的幺半群;
(SH3)剩余性:(x⊙y)→z=x→(y→z).
定义 3.2(1)称 (L,∧,∨,⊙,→,0,1)是剩余格[4],如果它满足
(R1)(L,∧,∨,0,1)是有界格;(R2)(L,⊙,1)可换的幺半群;
(R3)剩余性:x⊙y≤z当且仅当x≤y→z.
(2)称剩余格 (L,∧,∨,⊙,→,0,1)是 Rℓ-monoid[12],如果它满足可分性,即

(3)称剩余格 (L,∧,∨,⊙,→,0,1)是 MTL-代数[3],如果它满足预线性,即

(4)称 MTL-代数 (L,∧,∨,⊙,→,0,1)是 BL-代数[2],如果它满足可分性.
(5)称 BL-代数 (L,∧,∨,⊙,→,0,1)是 MV-代数[1],如果它满足对合性,即
例 3.1[13]设L={0,a,b,c,d,1}∨{(x,x)∈R2|x∈(2,3)},这里
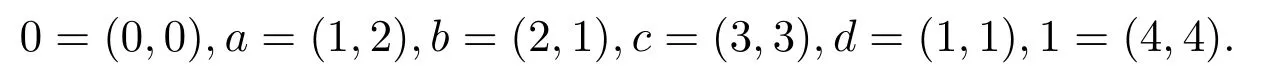
其上交运算∧、乘法运算⊙和蕴含运算→定义如下:
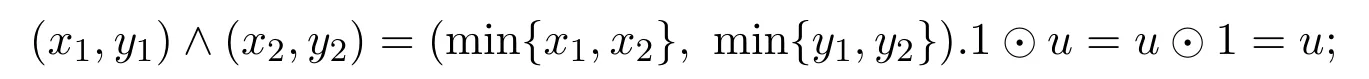
否则u⊙v=0.当u∧v=u,u→v=1;当u=1,u→v=v;否则u→v=c.则L是半-Hoop.但它不是∨-半格,因为a,b无上确界.此外,它不满足可分性,因为a⊙(c→a)a∧c.
例 3.2设L={0,a,b,c,d,e,1},序关系为

其上乘法运算⊙和蕴含运算→如表1:

表1 剩余格例子
则L是剩余格.但它不满足预线性,因为(b→c)∨(c→b)1.它不满足可分性,因为d⊙(d→b)d∧b;e⊙(e→b)/=e∧b;e⊙(e→d)e∧d.
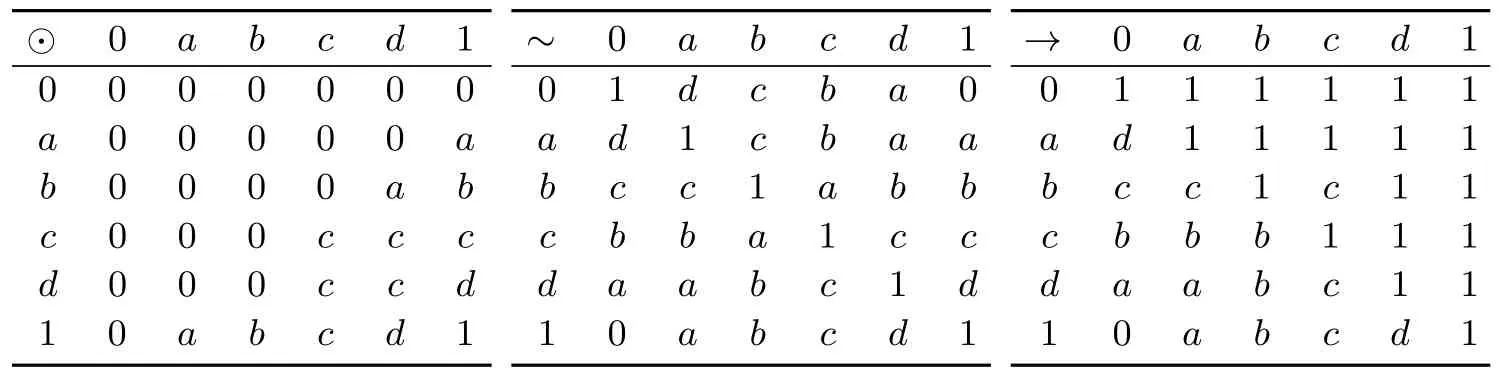
例 3.3[14]设L={0,a,b,c,1},序关系为0 表2 Rℓ-monoid 则L是Rℓ-monoid.但它不满足预线性,因为(a→b)∨(b→a)1. 例 3.4[15]设L={0,a,b,c,d,1},序关系为0 表3 MTL-代数 则L是MTL-代数.但它不满足可分性,因为c⊙(c→b)c∧b.此外,它显然不满足对合性. 例 3.5设L={0,a,b,1}是链,其上乘法运算⊙和蕴含运算→如表4: 表4 BL-代数 则L是BL-代数.但它不满足对合性,因为 例 3.6设L={0,a,b,c,1}是链,其上乘法运算⊙和蕴含运算→如表5: 表5 MV-代数 则L是MV-代数. 下面给出非链的MV-代数. 例 3.7设L={0,a,b,c,d,1},序关系为 其上乘法运算⊙和蕴含运算→如表6: 表6 MV-代数 则L是MV-代数. 下面以MV-代数为例从代数的观点说明模糊逻辑与经典逻辑之间的区别. (1)在经典的逻辑系统中,对任意的命题x,可得恒假命题对于ukasiewicz逻辑,由例3.6知b≡b,从而b∧b不是假命题.从经典逻辑观点看,b既不是真命题,也不是假命题,这意味着经典逻辑失效了.为解决这个问题,可以把0.5赋值给b,表示命题b是真的程度为0.5.因此必须把真值域从{0,1}扩大到更大的范围,从而得到了一种新的逻辑系统-模糊逻辑. (3)从极大滤子角度观察两者的区别,在经典逻辑系统中,由命题 2.2知布尔代数上所有极大滤子的交仅包含一个元素,它是恒真命题.在ukasiewicz逻辑中,这一结论不成立.在例 3.7中,{b,a,1}和{d,a,c,1}是滤子 (见定义 2.2),且他们是格L={0,a,b,c,d,1}上所有极大滤子,{b,a,1}∩{d,a,c,1}={a,1}.从而例3.7不是布尔代数.但发现了一个有意思的现象,在例3.7中,F={b,a,1}是格L={0,a,b,c,d,1}上的极大滤子,且F′={c,d,0},这里F′={x′|x∈F},容易验证F′=Fc.用定理2.1的观点看,在标准F下,虽然也能判断L中的元素的真假,但L不是布尔代数.因为在另一个标准G={d,a,c,1}下,G∩G′={a,d}∅,即a与a′=d既是真命题又是假命题,矛盾.基于这些观测,给出下面定理. 定理 3.1MV-代数L是布尔代数当且仅当格L上的任意极大滤子F满足F∩F′=∅,这里F′={x′|x∈F}. 证明由第2节内容知⇒显然成立.反之,设L是MV-代数.若存在x∈L满足x∧x′=b>0,则区间[b,1]是真滤子.从而存在极大滤子F使得F⊇[b,1],由此可得x,x′∈F.因此{x,x′}⊆(F∩F′).矛盾!这说明对任意的x∈L都有x∧x′=0.下面证明对任意的x∈L都有x∨x′=1.若存在x∈L满足x∨x′=c<1,则x∧x′=(x∨x′)′=c′>0.矛盾! 例 3.8[16]设 (G,+,−,0,∧,∨)是阿贝尔格序群,u∈G是强单位元 (∀x∈G,∃n满足x≤nu).在集合[0,u]⊆G上定义 则 ([0,u],∧,∨,⊙,→,0,u)是 MV-代数. MV-代数与格序群有着密切的联系,文献[16]证明了MV-代数范畴与有强单位元的阿贝尔格序群范畴是等价的;进而文献[17]证明了伪MV-代数范畴与有强单位元的格序群范畴是等价的.从而建立了格序群与MV-代数的联系,这说明可以把格序群中的概念和结论转化到MV-代数,反之亦然[18]. 为了用分析的方法研究代数结构的性质(例如收敛性),拓扑是一个很好的工具.拓扑格序群受到国内外学者的关注,得到了一系列的研究成果.这些工作自然可以转化到MV-代数中.文献[19]利用容许集C建立了格序群上的C-拓扑.在此基础上,文献[20]借助距离度量和滤子F定义了开F-球,进而以这些开球为基得到了MV-代数上的拓扑,这里不要求MV-代数是2-可分的,从而改进了文献[19]的工作,之后文献[21]给出了单和半单MV-代数的拓扑刻画.另外,一个有意思的工作是文献[22]利用domain的思想研究格序群,提出连续格序群的概念,进而产生C-拓扑,这对研究剩余结构上的拓扑有很好的启发. 定义 3.3[23]称映射s:B−→[0,1]为MV-代数B上的态,如果它满足 (S1)s(0)=0,s(1)=1; (S2)对任意的x,y∈B,若x⊙y=0,则s(x)+s(y)=s((x′⊙y′)′). 下面从概率的角度解释态的定义.设F有限且是σ-代数,p是F上的概率.则F是布尔代数.下面说明p是 MV-代数F上的态.首先p满足(S1),因为空事件的概率是 0,全空间事件的概率是 1.其次p满足 (S2),若A,B∈F是不相容事件,即A∧B=0,则p((A′⊙B′)′)=p(A∨B)=p(A)+p(B).需要注意的是,当把布尔代数F看作是MV-代数时,⊙与∧一样,从而 (A′⊙B′)′=A∨B.在概率论中条件概率是重要的内容,如何把条件概率推广到MV-代数中,这是一个有意义的问题. 在态理论研究中,Bosbach态和Riečan态是重要的两类态.文献 [24]研究了剩余格上两类特殊的广义Bosbach态,解决了三个公开问题.文献[25]研究了MTL-代数上的 Bosbach态和Riečan态,证明了 MTL-代数上存在 Bosbach态当且仅当奇异滤子存在.由于逻辑代数的态不是它自身的算子,因而具有态的代数一般不是泛代数,所以不能自然诱导断言逻辑.为了给模糊事件的概率提供代数基础,文献[26]运用概率的方法引入了一种可代数化逻辑,它的等价语义恰好是具有内态的MV-代数簇.在此基础上,很多学者在剩余结构上研究了内态理论,例如:态半-Hoops[27]、态剩余格[28]、态 Rℓ-monoids[29]和态 BL-代数[30]. 下面给出特殊的一类半-Hoop,即它是半-Hoop且满足可分性. 定义 3.4[5]称 (H,⊙,→,1)是 Hoop,如果它满足 (H1)(H,⊙,1)可换的幺半群;(H2)剩余性:(x⊙y)→z=x→(y→z); (H3)可分性:x⊙(x→y)=y⊙(y→x);(H4)x→x=1. 需要注意的是,由可分性知Hoop是交半格,从而Hoop一定是半-Hoop.另一方面,Hoop一般情况下没有格结构,从而Hoop未必是剩余格.若Hoop是有限的,则它一定是剩余格.因此构造一个例子说明(H,⊙,→,1)是Hoop但不是剩余格,这是有价值的工作,但有一定的难度.因为H必须是无限的.另外由于Hoop还要满足可分性,这意味着运算⊙与→有非常苛刻的兼容性,严重降低了构造例子的自由度.反之,由例3.2知剩余格未必是Hoop.由例3.3知存在代数结构,它既是剩余格又是Hoop. 模糊型理论是一类高阶模糊逻辑,它以模糊相等作为主要联结词.为给模糊型理论寻找更为广泛的代数结构.文献[8]提出了EQ-代数.EQ-代数定义在有最大元的交半格上,有两个逻辑运算:合取运算和模糊相等运算,具体定义如下: 定义 4.1[8]称 (E,∧,⊙,~,1)是 EQ-代数,如果对任意的x,y,z,t∈E满足 (EQ1)(E,∧,1)是1为最大元的∧-半格; (EQ2)(E,⊙,1)是幺半群且⊙保序;(EQ3)自反性:x~x=1; (EQ4)替代公理:((x∧y)~z)⊙(t~x)≤z~(t∧y); (EQ5)全等公理:(x~y)⊙(z~t)≤(x~z)~(y~t); (EQ6)单调性:(x∧y∧z)~x≤(x∧y)~x; (EQ7)有界性:x⊙y≤x~y. 定义 4.2[8](1)称 EQ-代数 (E,∧,⊙,~,1)是好的,如果满足x~1=x. (2)称 EQ-代数 (E,∧,⊙,~,1)是剩余的,如果满足 (x⊙y)∧z=x⊙y当且仅当x∧((y∧z)~y)=x. EQ-代数是剩余格的推广,两者主要区别是:EQ-代数诱导的蕴含算子 与乘法算子不再是伴随的.因此,EQ-代数未必是剩余格(见下面的例子).需要注意的是,虽然有限剩余EQ-代数是剩余格,但剩余EQ-代数不是剩余格[13].在例3.1基础上,定义x~y:=(x→y)∧(y→x),则 (L,∧,⊙,~,1)是剩余 EQ-代数,但不是剩余格,因为它不是并半格. 例4.1[31]设E={0,a,b,c,d,1},序关系为0 表7 EQ-代数 则(E,∧,⊙,~,1)是EQ-代数,但不是剩余格.因为⊙不满足交换性,例如 设 (E,∧,⊙,~,1)是 EQ-代数,且⊙1≤⊙(⊙1≤⊙定义为 则(E,∧,⊙1,~,1)是EQ-代数.从中发现EQ-代数的乘法与模糊相等运算存在较弱的关系,因此Jenei忽略乘法运算,提出相等代数,具体定义如下: 定义 4.3[9]称(E,∧,~,1)是相等代数,如果对任意的x,y,z∈E满足 (EA1)(E,∧,1)是1为最大元的∧-半格; (EA2)x~y=y~x;(EA3)x~x=1;(EA4)x~1=x; (EA5)若x≤y≤z,则x~z≤x~y,x~z≤y~z; (EA6)x~y≤(x∧z)~(y∧z);(EA7)x~y≤(x~z)~(y~z). 给定一个好的EQ-代数,舍弃相乘运算可得相等代数.特别地,例4.1是好的EQ代数,从而它是相等代数.反之,给定一个相等代数,如何诱导出一个好的EQ-代数使得两者具有相同的相等运算.考虑有最小元的相等代数,设(E,∧,~,0,1)是相等代数.定义⊙∗为 1⊙∗x=x⊙∗1=x;u⊙∗v=0,其它.则 (E,∧,⊙∗,~,0,1)是相等代数诱导的好的EQ-代数.令PE={⊙|(E,∧,~,0,1)是相等代数且E,∧,⊙,~,0,1)是好的EQ-代数},则PE非空,因为⊙∗∈PE.定义⊙1≤⊙2为∀x,y∈E,x⊙1y≤x⊙2y,这里⊙1,⊙2∈PE.则 (PE,≤)是下集.注意到在 EQ-代数中x⊙y≤x∧y,如果∧∈PE,则(PE,≤)有最小元⊙∗和最大元∧.但∧∈PE不成立,例4.1是相等代数,但(EQ4)不成立,因为((b∧1)~1)∧(0~b)≤1~(0∧1)不成立.因此给定一个相等代数(E,∧,~,0,1),如何诱导出一个好的EQ-代数且其乘法是(PE,≤)中的极大元,这是一个有趣的问题,值得进一步的研究. EQ-代数聚焦于模糊相等连接词,为模糊型理论研究提供了新思路,因此受到国内外学者的关注,出现了一系列有价值的成果.文献[32]从代数的观点,考虑乘法与模糊相等的兼容性提出了相容EQ-代数.文献[33]从拓扑的观点,利用邻域系构造拓扑使得它是拓扑EQ-代数.同时,文献[34-37]研究了EQ-代数上态,内态和广义态理论,拓展了态的研究范围,大部分成果被收录在专著[38]. 本文讨论了9种代数结构及其关系.同时也追踪了这些结构与格序群,拓扑和概率相结合的文献.特别地,本文证明了布尔代数上极大滤子恰是赋值映射,以独特的视角说明布尔代数是经典逻辑,进而从代数的视角揭示了经典逻辑与模糊逻辑的不同.为了更好地理解这些代数结构,给出了相应的例子.因为例子是对代数结构及其理论的有力说明,也是把相应理论运用到实际问题的基础. 作为进一步的研究,给出下面公开问题: (1)概率模型在MV-代数上的推广是态理论,条件概率及分布函数在MV-代数上的推广是什么呢? (2)构造一个例子,它是Hoop,但不是剩余格. (3)给出一个算法,能找到一个有限交半格的所有EQ-代数. (4)如何从相等代数诱导出一个好的EQ-代数?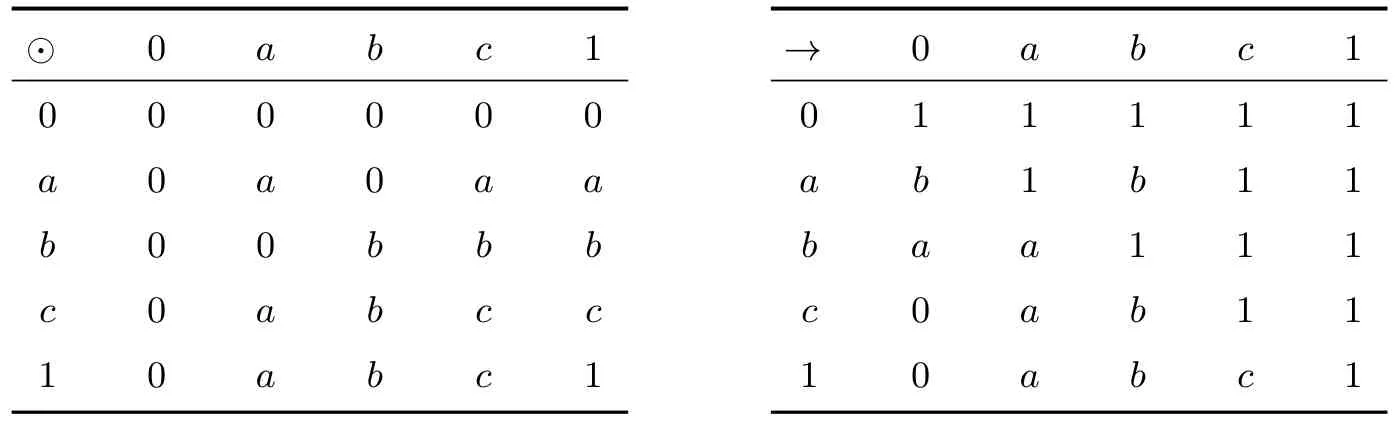



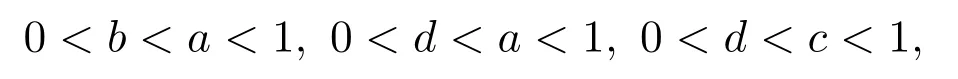


4 高阶逻辑与 EQ-代数和相等代数
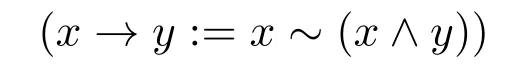
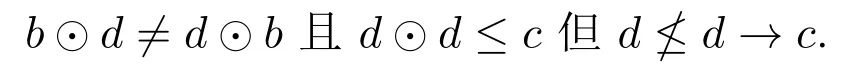

5 总结与展望
