关于几类矩阵的注记

刘合国,赵静

(湖北大学数学与统计学学院,湖北 武汉 430062)

1 引言

为方便计,本文用 diag(a1,a2,···,an)表示对角线元素是a1,a2,···,an的n阶对角阵,用Cn表示基本的n阶循环置换矩阵,V(x1,x2,···,xn)表示关于x1,x2,···,xn的Vandermonde矩阵,即

一般地,本文采用的术语和符号是标准的,参见文献[1-2].

特殊矩阵在矩阵分析里起着核心的作用.循环矩阵,Vandermonde矩阵,Hilbert矩阵以及Cauchy矩阵是常常碰到的几类矩阵,它们在各种数学理论里发挥着重要的作用,见文献[3].现在用统一的思想来重新处理这些矩阵的几个基本问题,由此可以看到它们之间的本质联系,以及它们与多项式理论,线性方程组理论之间的深刻联系,这为理解这些经典结果提供了又一种思考方式.

具体说来,运用 Cramer法则和 Lagrange插值公式来计算 Vandermonde矩阵,Hilbert矩阵和Cauchy矩阵的行列式,逆矩阵以及逆矩阵的所有元素之和等问题,用Lagrange插值公式来处理一个涉及循环矩阵的矩阵分解问题.这种处理问题的思路和方法与文献[4-5]是一致的,其最核心的工具是插值,这是中国剩余定理的本质所在.在理解这点后,本文可以看做是文献[4-5]的延伸.

本文反复用到的一些基本事实如下.

2 关于一个矩阵分解的定理

熟知每个n阶循环矩阵都可表示为关于Cn的多项式,这类矩阵在理论和应用方面都具有重要性,见文献 [6].从下面的矩阵恒等式可知Cn与 diag(1,ω,···,ωn−1)是相似的,

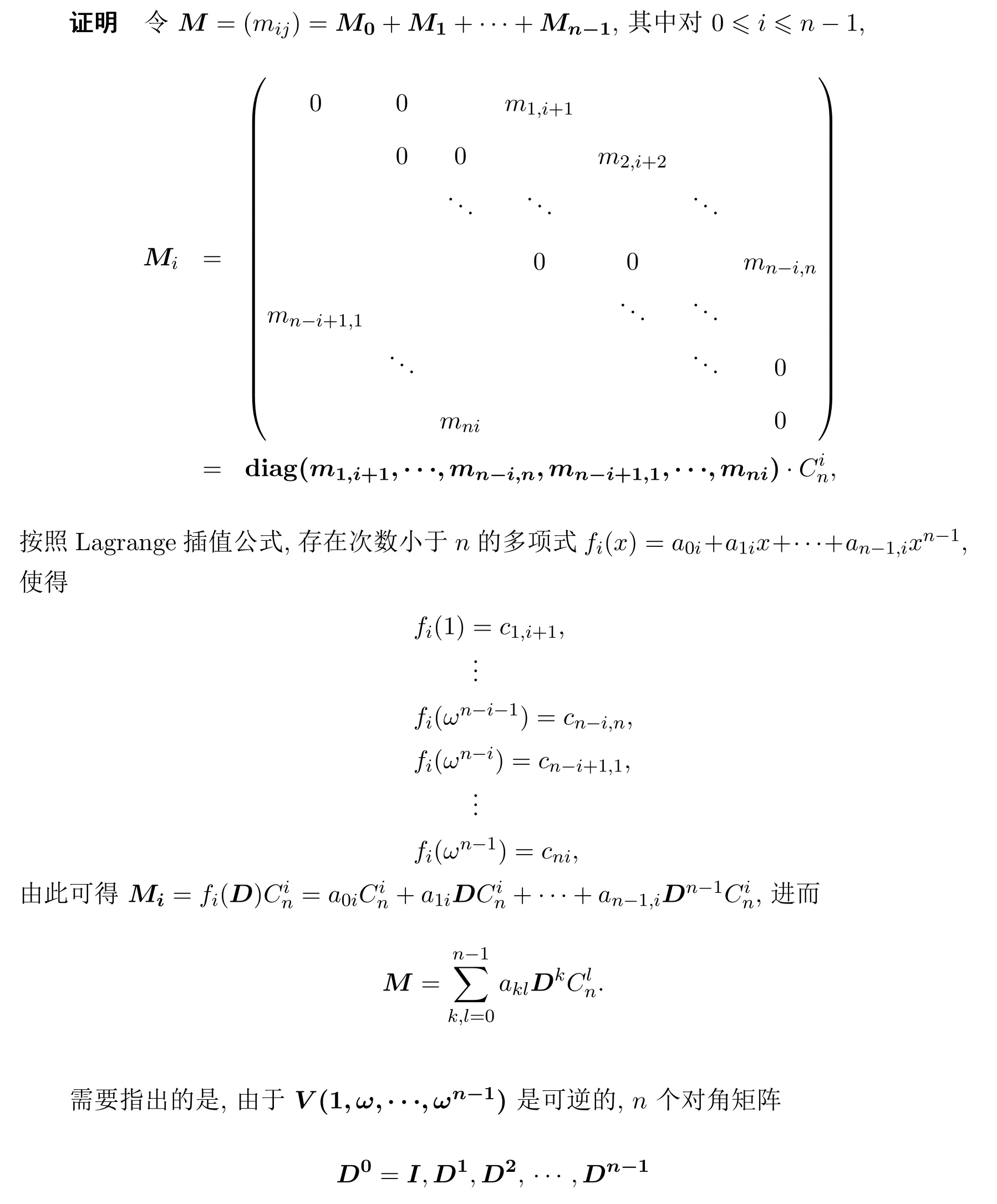
是线性无关的,故每个对角矩阵都是它们的线性组合,文献[7-8]由此得到定理2.1的证明.注意到Lagrange插值公式能够由多种方式推导出来,包括运用Vandermonde行列式进行证明,参见文献[4,9],这样本文的证明与文献[7-8]的证明在本质上是一致的.

定理2.1可推广成更一般的形式.

3 Vandermonde矩阵

Vandermonde矩阵是最熟悉的矩阵之一,它在线性代数 (高等代数)里时常出现,参见文献[10-11].下面的结论是最基本的,这里给出一个多项式证明.

4 Hilbert矩阵

5 Cauchy矩阵

文献[12-15]处理了某些与Vandermonde矩阵,Hilbert矩阵,Cauchy矩阵相关的问题.不论是就理论还是就应用来说,特殊矩阵都是值得关注的研究对象.熟练地运用基本工具去解决特殊矩阵的基本问题,是研读矩阵分析的基本功.