天线随机振动分析与设计优化

付佐红，董高彬，程驰青，邵惠琳

(1. 中电防务科技有限公司，南京 210007；2. 徐州工业职业技术学院，江苏 徐州 221140)

0 引 言

随着飞行器朝着高速度、高机动的方向不断发展，机上的振动环境越发严酷，对设备的耐振动性能要求也日益苛刻，统计表明40%的飞机事故与振动有关[1]。机载卫星天线能够对目标卫星定向和跟踪，建立数据传输链路，从而实现通讯[2]。为保证机载天线在振动环境下稳定可靠，避免机体振动损坏天线，本文通过降低应力集中、减少转接件、减轻质量等方式来提高天线固有频率、增加天线刚度，从而提高天线抗振动能力[3-4]。

1 天线概况及其安装背景

该款天线安装位置为直升机旋翼顶端，如图1所示，该位置振动量级较大，加之该天线具有百兆网口和SDI视频功能，导致功放功率、体积和重量均大幅增加，对结构件的强度、天线整机的抗振动能力提出较高要求，现行该型号机载天线无法满足，须对天线结构进行优化设计。

图1 天线装机位置示意图

天线结构上由天线面及馈电网络、俯仰/方位传动机构、模块安装组件等部分构成，如图2所示，天线以横梁支架为安装主体，变频器、功放、电源等模块安装于模块安装板上，俯仰/方位传动机构带动天线面及馈电网络的任意方向旋转，使天线面始终正对通信卫星，从而实现所需通信功能。

图2 天线结构框架示意图

2 天线结构优化

2.1 减少应力集中

俯仰天线面及馈电网络部分与俯仰传动机构中的扇形齿轮相连接，俯仰电机驱动俯仰小齿轮，从而带动天线面进行俯仰运动。天线面与馈电网络部分重量通过极化网络安装板全部压在左右俯仰支架上。在实际振动试验过程中，左右俯仰支架均有不同程度的裂隙，为分析该结构受力情况，使用有限元方法对该天线进行静应力、模态计算、随机振动分析。

2.1.1 建立模型与前处理

本文的三维模型均在UG软件中建立，为计算方便，简化天线三维模型中各齿轮轮齿、螺纹，将模型导入有限元软件ANSYS后进行网格划分。网格设置为四面体网格，网格总数约741 000个，传动部分网格可适当密些，天线面网格可适当稀疏，最大网格尺寸不超过3 mm。

该款机载天线振动环境为随机振动，根据国标GJB150.16A设置振动条件如图3所示，其中f取500 Hz，加速度谱面密度W0=0.001 g2/Hz，W1=0.01 g2/Hz。结构件材料为铝合金LY12，天线面材料为碳纤维。设置天线下方安装接口为固定面、振动条件施加面。

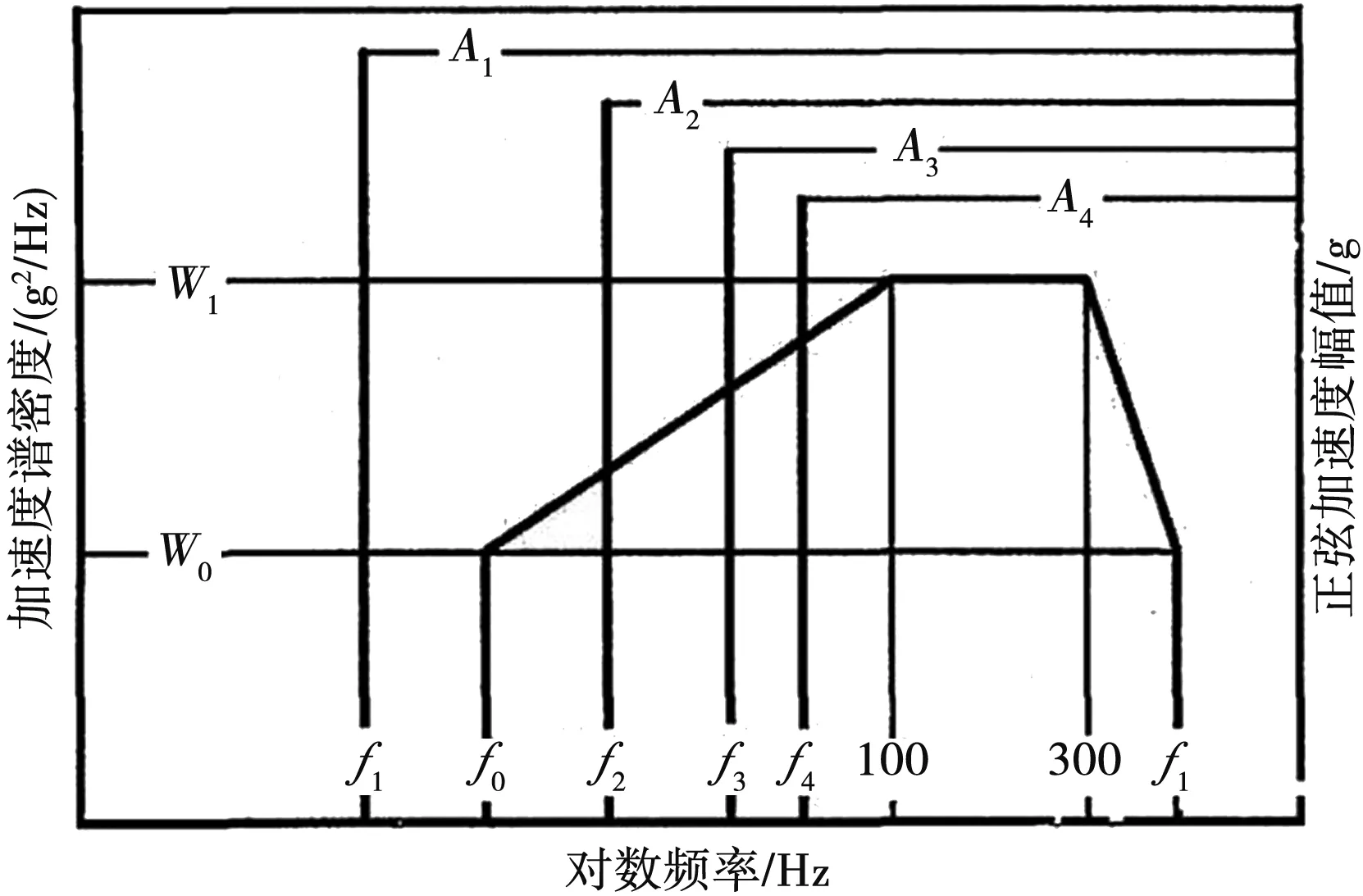
图3 施加振普图

2.1.2 仿真结果

由于天线安装在天线罩内，除重力、飞机起落加速度外几乎不受其他静应力影响，仿真结果与实际无异，所有结构件所受应力均不会超过材料屈服强度许用值。

由于在振动试验过程中断裂零件为左俯仰支架，因此随机振动仿真只关注该零件。左右俯仰支架应力云图如图4所示。

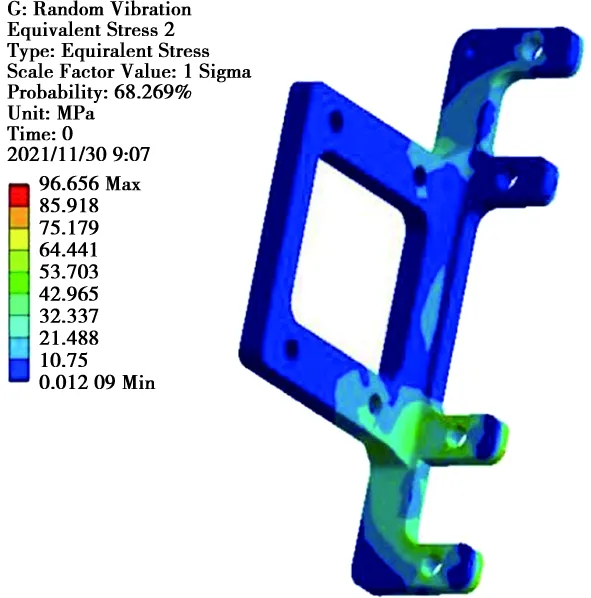
图4 俯仰支架应力云图

可以看出，在1σ条件下，零件根部应力最大值为96.6 MPa，则3ε条件下应力可达289.8 MPa，临近LY12铝合金屈服强度325 MPa。安全系数μ=2-(325/289.8)=1.12，该零件安全系数过小，在实际使用中损坏的可能性极大，因此对该零件进行优化设计。

2.1.3 正交实验设计

本文通过正交实验对该零件进行优化改进，图5给出了该俯仰支架结构件优化流程。

图5 俯仰支架结构优化流程图

本文选取该左俯仰支架厚度、断裂处圆角大小、是否有斜筋3个参数作为因素，每个因素两水平，正交实验设计如下：

支架厚度A：6 mm、8 mm(分别记为A1、A2)；

断裂处圆角大小B：7 mm、10 mm(分别记为B1、B2)；

是否有斜筋C：无、有(分别记为C1、C2)。

表1、表2分别为正交方案设计与正交实验结果统计。

表1 正交方案设计

表2 有限元仿真结果统计

正交实验得到的结果较为浅显，还要进行更深入的计算和分析：利用实验结果分析结构件应力、结构件重量等指标随各因素变化的规律，以及各因素对两个实验指标影响轻重顺序；正交实验并不是简单地将各因素所有水平进行了排列组合，本文仅仅做了部分实验，不能确保各因素中的最优组合刚好在所选取的实验组合中，须找出各因素各水平的最佳组合。

极差分析法是在正交实验设计中较为常用的结果分析方法，计算简单，结果直观。本次实验有2个指标：一是零件所受最大应力应小于铝合金屈服强度，以保证LY12铝合金不断裂；二是零件重量，机载零件重量锱铢必较，在零件所受应力较小的条件下首选重量较轻的各因素的参数组合。先采用极差直观分析法分析实验过程中各因素对零件所受最大应力、重量这两个单一指标的影响，综合分析比较不同因素对各指标的影响，经取舍确定最优的各因素不同水平下的组合方案，最大应力和重量实验结果分析分别如表3、表4所示。

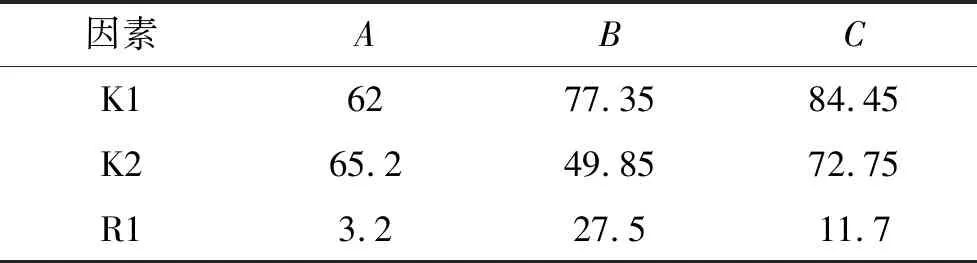
表3 正交实验最大应力指标结果分析(单位MPa)

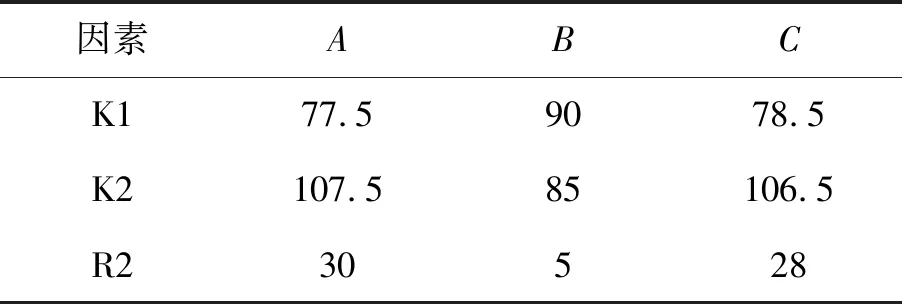
表4 正交实验重量指标结果分析(单位g)

表中为相同指标每个因素下各水平的平均，即

(1)

定义R为该实验中所选取的各因素极差，其意义是实验中某一因素各水平实验指标的最大值与最小值之差，即

R=maxKi-minKi

(2)

结合上述分析结果，最大应力极差值R1A很小，即支架厚度对优化应力集中意义不大，但R2A相对较大，说明增加零件厚度会显著增加其质量，而对机载产品来说，重量“寸土寸金”，因此俯仰支架厚度选择6 mm即可。圆角大小及是否增加斜筋对最大应力指标影响较大，分别选取最佳水平B1、C2。故分析得到最佳水平组合为A1、B2、C3，即支架厚度6 mm，断裂处圆角大小R为10 mm，两侧设计斜筋加固。

2.1.4 俯仰支架优化结果

优化后仿真结果如图6所示，应力云图中已无应力集中位置，最大应力27.4 MPa。根据3ε原则，该俯仰支架所受应力为82.2 MPa，远小于LY12铝合金屈服强度325 MPa，可认为其不会断裂，满足设计要求。

图6 优化设计后俯仰支架应力云图

本实验仅以实际使用中断裂的俯仰左支架为例，利用正交实验法对其进行优化设计，该方法计算简单，仅须做各因素部分水平的组合即可分析出各因素对指标的影响，具有很好的推广性，天线其他结构件亦可使用该方法进行优化设计。

2.2 提高模块安装组件的固有频率

天线模块安装板上有功率放大器、变频器、三合一电源、伺服控制模块等，通过螺接方式固定于主轴横梁上。根据振动实验及实际使用情况，电源、变频器等模块常出现开焊、板件损坏等问题，本文拟通过提高模块安装组件固有频率来增强其抗振动的能力。将模块安装组件简化为一简单悬臂梁，如图7所示。

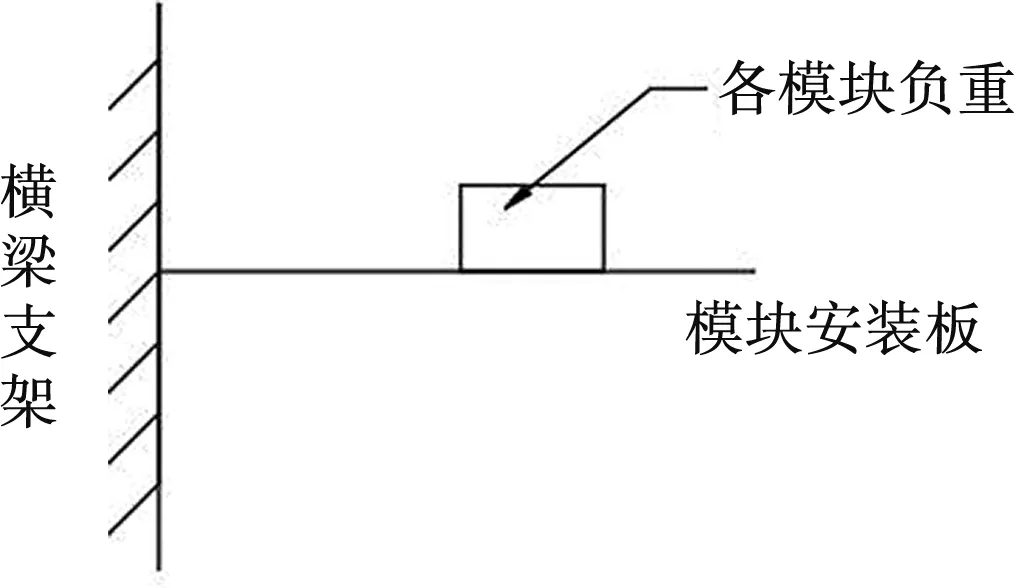
图7 模块安装组件简化图

针对欧拉-伯努利梁，其自由运动微分方程为

(3)

利用分离变量法，令

w(x,t)=W(x)T(t)

(4)

则式(3)化简为

(5)

(6)

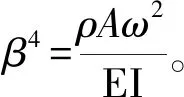
梁的固有频率ω的解为

(7)

式中，β取值与梁的边界条件有关。

悬臂梁其边界条件如下：

X=0时，

X=L时，

由材料力学可知梁末端静挠度为

(8)

则弹性系数为

(9)

式中，P为等效重力；l为重心距离固定端距离；EI为模块安装组件弯曲刚度。

可推出模块安装组件振动微分方程：

(10)

即

(11)

则系统频率为

(12)

对天线进行模态计算，计算结果如表5所示。

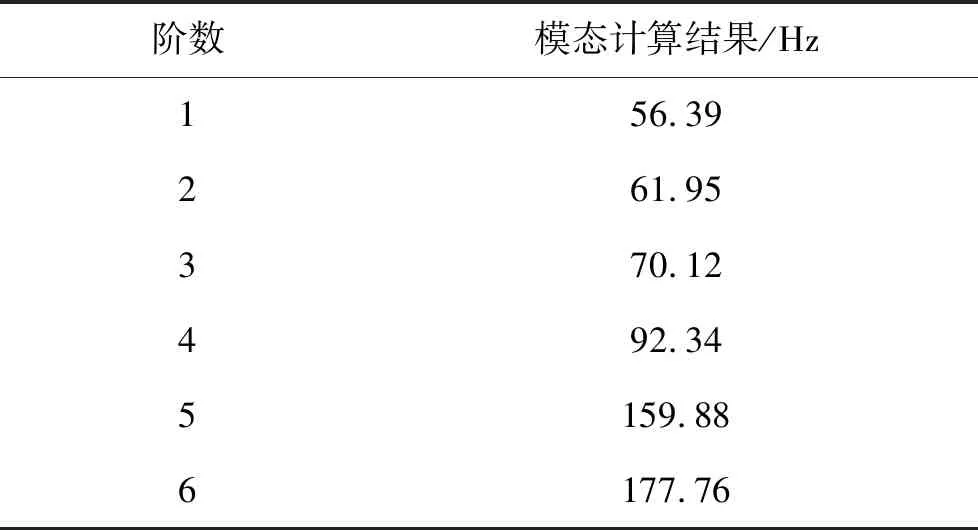
表5 天线模态分析结果

可见该款天线一阶、二阶模态较低，根据装机飞行经验以及相应振动实验，一般只须关注前几阶模态数值，因为低阶固有频率对设备影响较大，结构件所受应力较大、变形明显，因此提高设备一、二阶固有频率就可显著提高设备的耐振动性能。

由上述计算可知，减轻系统重量m、缩小重心至固定端距离l，均可有效提高系统的固有频率，因此尝试去掉电源模块与伺服控制器之间的转接件，直接在三合一电源盖板上攻螺纹孔，将伺服控制器直接安装于电源模块盖板上方。为缩小重心至模块固定端的距离，伺服控制器的摆放位置可尽量向内侧推进。

对改进后的结构进行仿真分析，模态计算结果如表6所示。可以看出该款天线一阶频率大于60，根据装机经验可认为该款天线刚性较好，抗振动性能有较大改善。理论一阶振型位移应变云图如图8所示。

图8 理论一阶模态位移应变云图

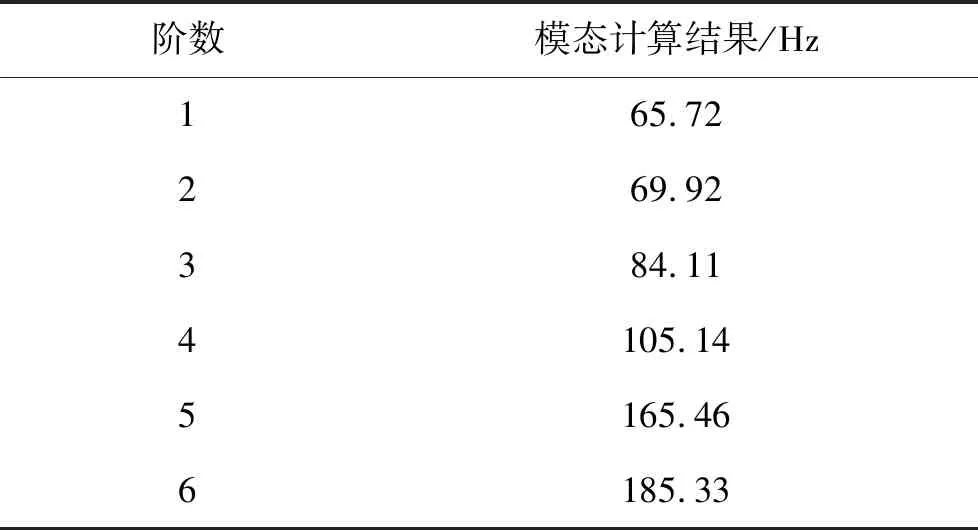
表6 改进后天线模态分析结果

2.3 增强天线抗振动性能的其他方式

除上述方法外，其他一些方法也可增强该款天线的抗振动能力，如减轻质量、增加阻尼等。

由频响函数可知，其他条件不变，减轻系统重量可有效提高系统固有频率。在保证结构强度的前提下各大型零件进行合理的轻量化设计，图9为横梁支架的背部轻量化设计示意图，其背部的减重设计不但大幅减轻了结构件重量，而且余料以加强筋的形式保证了结构件强度[5-7]。

图9 横梁支架背部轻量化设计示意图

由频响函数可知，增加阻尼不能改变设备的固有频率，但是可以降低共振放大。可在脆弱模块部分增加被动隔振，比如在安装功放模块时，在模块安装板与功放之间位置加装钢丝绳隔振器，从而将振动能量转化为隔振器的位移，以保护功放等脆弱模块。

3 结束语

本文通过正交实验优化了部分零件结构，减少了天线结构件应力集中，并通过减少转接件的方式提高了天线固有频率，从而增强了天线的抗振动性能。系列方法具有良好的推广性，为机载产品的结构优化设计以及实际生产提供了参考。