双层网络上不同时间演化尺度的耦合传播动力学

曾颖琪 唐明

摘要： 基于双层网络构建了一个具有不同时间演化尺度的耦合传播模型—噪声投票-SIR （Susceptible- Infected-Recovery）传播耦合模型.该模型可以用微观马尔可夫链数值分析方法来描述.大量的蒙特卡洛模拟实验验证了这一数值分析方法的准确性. 研究发现 ， 耦合模型中发生了相变类型的跨越现象：当意见形成过程中的噪声比较小的时候 ， 消息传播规模和正（+）意见比例随着传播速率的变化发生不连续相变 ， 与此同时还出现了磁滞回线和双稳态现象 ， 并能观察到全局意见共识的形成;当噪声较大时 ， 两个动力学过程的序参量随传播速率的改变发生连续相变.

关键词：双层网络;  时间演化尺度;  耦合传播;  相变;  跨越现象

中图分类号： TP393    文献标志码： A    DOI： 10.3969/j.issn.1000-5641.2022.02.006

Coupled propagation dynamics of different time evolution scales on double-layer networks

ZENG Yingqi1 ，  TANG Min1，2

（1. School of Communication and Electronic Engineering， East China Normal University，Shanghai  200241， China;2. School of Physics and Electronic Science，East China Normal University， Shanghai  200241， China）

Abstract： Using  double-layer  networks，  we  constructed  a  coupled  propagation  model （Noisy  Voter - Susceptible-Infected-Recovery） with different time evolution scales. This coupled spreading process can be characterized by numerical analysis method of microscopic Markov chain theory. We verified the accuracy of the proposed numerical analysis method using a large number of Monte Carlo simulation experiments. We found a crossover phenomenon of the phase transition type in the coupled model. Specifically， when the noise in the opinion formation process is relatively small， the information propagation scale and the proportion of positive opinions change discontinuously with the information transmission rate. At the same time， the hysteresis loop and bistability phenomenon appear， in which the phenomenon of global consensus can be observed. When the noise is large， the order parameters of these two dynamic processes vary continuously with the transmission rate.

Keywords： double-layer  networks;   time  evolution  scales;   coupled  propagation;   phase transition; crossover phenomenon

0  引言

復杂网络的动力学研究[1-2]是网络科学的研究重点之一 ， 包括渗流[3-4]、同步[5]、意见形成[6]、疾病和消息传播[7]等 ， 它揭示了物理、人类社会和生物演化过程中的新现象 ， 同时也加深了人们对许多复杂系统的具体功能及其演化机制的了解.最近的研究表明 ， 孤立的动力学过程无法完全描述实际复杂系统的各种现象和机制[8-11]. 事实上 ， 许多复杂系统是由多个相互作用的子系统构成的 ， 这些复杂系统可以用多层网络来描述 ， 如多个社交平台相互作用的多层社交网络、多种交通途径协同耦合的多层交通网络等.在多层网络上 ， 不同网络层的动力学过程的类型通常不同 ， 如不同传染病相互影响彼此在人群中的传播过程[12-14]、由不同动力学过程描述的大脑神经系统和营养传输系统之间的相互作用[15]. Soriano-Paños 等[16]在 2019年提出了一个基于多层网络的耦合动力学模型 ， 该模型考虑了人群意见同步过程和消息传播之间的相互作用.对多层网络上耦合动力学过程的研究是至关重要的 ， 这将有助于建模、预测和控制真实的复杂系统[17-19].

以往关于多层网络上耦合动力学的研究 ， 大多假设了不同网络层上动力学过程的时间演化尺度是一致的 ， 如关于流行病的危机意识和流行病传播过程的时间演化尺度是相同的;而对于不同时间演化尺度的耦合动力学研究还未得到人们的广泛关注.人类社会中 ， 人群意见共识的形成过程和消息传播过程是相互影响的[20]. 由于它们的时间演化尺度不同 ， 人们一直未能深入了解它们之间相互作用所带来的影响. 以民主选举事件为例 ， 当民众进行某选举投票时 ， 一方面 ， 民众通常会受到与候选人相关消息的影响;另一方面 ， 民众更倾向于所传播的他们感兴趣的消息.更为重要的是 ， 在现代社交媒体上消息传播的速度是非常快速的 ， 往往1 d 左右就经历了从产生、爆发到消亡的整个过程;然而民众对政治意见的改变大多是一个较慢长的变化过程， 如2016年英国脱欧公投和2016年美国总统选举等事件.鉴于此 ， 本文基于双层网络 ， 构建了一个具有不同时间演化尺度的相互耦合传播模型—噪声投票-SIR（Noisy Voter–Susceptible-Infected-Recovery， NV-SIR）传播耦合模型;同时发展了一套微观马尔可夫链（Microscopic Markov Chain Approach， MMCA）数值分析方法来描述此模型;在大规模合成双层网络上进行的大量蒙特卡洛（Monte Carlo， MC）模拟实验 ， 验证了此数值分析方法的准确性.

1  模型

为了描述多个动力学系统相互影响的物理机制 ， 本文考虑了1 个有着 M =2層的多层网络 ， 表示节点间不同的关系[21-22]. 如图 1（a）所示 ， 在 A 层考虑意见形成的动力学过程 ， 它是由噪声投票（NV）模型驱动[23] ， 将其称之为投票层. 噪声投票模型在经典投票模型[24]的基础上引入噪声概念. 在 B 层 ， 研究了在线上社交系统中的消息传播动力学过程 ， 这一过程遵循经典的 SIR 传播模型[25] ， 将其称之为信息层.

如图 1（a）所示 ， 在 A 层网络中 ， 每个节点可能处于2种状态中的一种：正（+）意见状态或负（−）意见状态. 这两种状态之间可以相互转化 ， 转化的动力一方面来自邻居的影响 ， 另一方面来自噪声激发的翻转. 本文用 v 表示这两种状态自发地相互转换的速率 ， 亦可称之为噪声参数;用 h 表示节点受到邻居影响的程度， 亦可称之为相互作用参数或耦合强度.例如， “+”意见状态的节点以v 的速率转化为意见相反的“–”意见状态 ， 并且还会以邻居中相反意见的比例乘相互作用参数（h）的速率翻转. 在 B 层网络中 ， 每个节点可能是3 种状态中的某一种 ： S （Susceptible）状态、I （Infected）状态和 R （Recovery）状态. 将 S状态节点定义为不知道消息的节点;定义 I状态节点对应活跃用户（传播者）， 这些用户将消息扩散到其他人群;定义 R状态节点对应的是对传播消息失去兴趣的用户. 本文用 b 表示 S 状态节点转换为 I状态的速率 ， 亦可称之为传播速率;用µ表示 I状态节点转换为 R 状态的速率 ， 亦可称之为恢复速率.

用邻接矩阵 A =（aij）和B =（bij）分别表示支持 NV 过程和 SIR 过程的网络. 如果在 A 层或 B 层中节点i 和j 之间存在连边 ， 则aij = 1或bij = 1 ， 否则aij = 0或bij = 0. 动力学状态量 Pi+（t）表示节点 i 的 A 层代理意见为“+ ”的概率 ， 它是随时间变化的 ， Pi+（t）∈ [0， 1]. 由于“+”意见状态和“–”意见状态是对立的 ， B 层对 A 层的影响函数在两种翻转概率中有细微差别： h ⇒ hξ （t）或h ⇒ hξ i （t） ， 其中 ， 符号⇒表示 A 层的参数 h 受到 B 层的影响 ， ξ（t）是节点 i 在 A 层处于“ –” 意见时 B 层对 A 层的影响函数. A 层中节点i 的状态由“–”意见→“+”意见的概率和由“+”意见→“–”意见的概率分别为

（1）

其中 ， kA，i表示节点i 在 A 层的度值大小 ， ξ i （t）是节点i 在 A 层处于“+ ”意见时 B 层对 A 层的影响函数. 使用动力学状态量 Si（t）、Ii（t）、Ri（t）分别表示节点 i 的 B 层代理为 S 状态的概率、 I 状态的概率、 R 状态的概率 ， 它们是随时间变化的 ， Si（t）， Ii（t）， Ri（t）∈[0， 1].对于节点i 来说 ， 其是否变为活跃用户不仅仅取决于参数β 的大小 ， 还受到该节点在投票层意见的影响β ⇒βψi （t） ， 其中 ， 符号⇒表示 B 层的控制参数β受到 A 层的影响 ， ψi （t）是 A层节点i 对 B层节点i 的影响函数. 首先， 在网络中随机地选择一些节点作为传播种子的节点 ， 其他的节点都是 S 状态. 每个时间步 S状态节点以βψi （t）的速率被它的 I状态邻居劝服 ， 与此同时每一个 I状态节点会以µ的速率恢复成 R 状态.

如图 1（b）、图 1（c）所示 ， 本文引入了一种描述时间尺度不同的动力学过程之间相互作用的耦合方法：假设 B 层网络上的动力学过程演化速度比 A 层快 ， 即投票层的更新速度远小于信息层 ， 每当 A 层网络状态更新一次 ， B 层网络的动力学就演化到稳定或终结的状态. 因此对于 A 层的投票过程 ， 只会受 B 层上消息扩散的最终局面的影响.

接下来考虑不同层的动力学过程之间相互作用的影响. 如图 1（d）所示 ， iA 表示 A 层节点 i， iB 表示 B 层节点 i， 函数ψi （t）表示 A层节点i 对 B层节点i 的影响. 考虑到 A 层节点意见的对称性 ， 不妨设定消息的扩散依赖于 A 层的“+ ”意见 ， 并且“+”意见共识的形成依赖于消息扩散.详细的层间影响函数的值如表 1所示.

由表1可知 ， 如果 iA 的状态是 “– ”意见 ， 那么根据衰减因子 0⩽ ϵ⩽ 1降低消息扩散的能力 ， ψi （t）= 1− ϵ; 反之则加强其能力 ， ψi （t）= 1+ ϵ. 类似的 ， 函数ξ （t）和ξ i （t）表示iB 的状态对iA 的影响：如果节点 i 在 A 层、B 层的联合状态为[+S] ， 则由 “+”意见→“– ”意见翻转的趋势被增强为ξ i （t）= 1+ϵ;如果联合状态是[−S] ， 则由“–”意见→“+”意见翻转的趋势被削弱为ξ （t）= 1− ϵ.

2  方法

2.1  微观马尔可夫链数值分析方法[26-27]

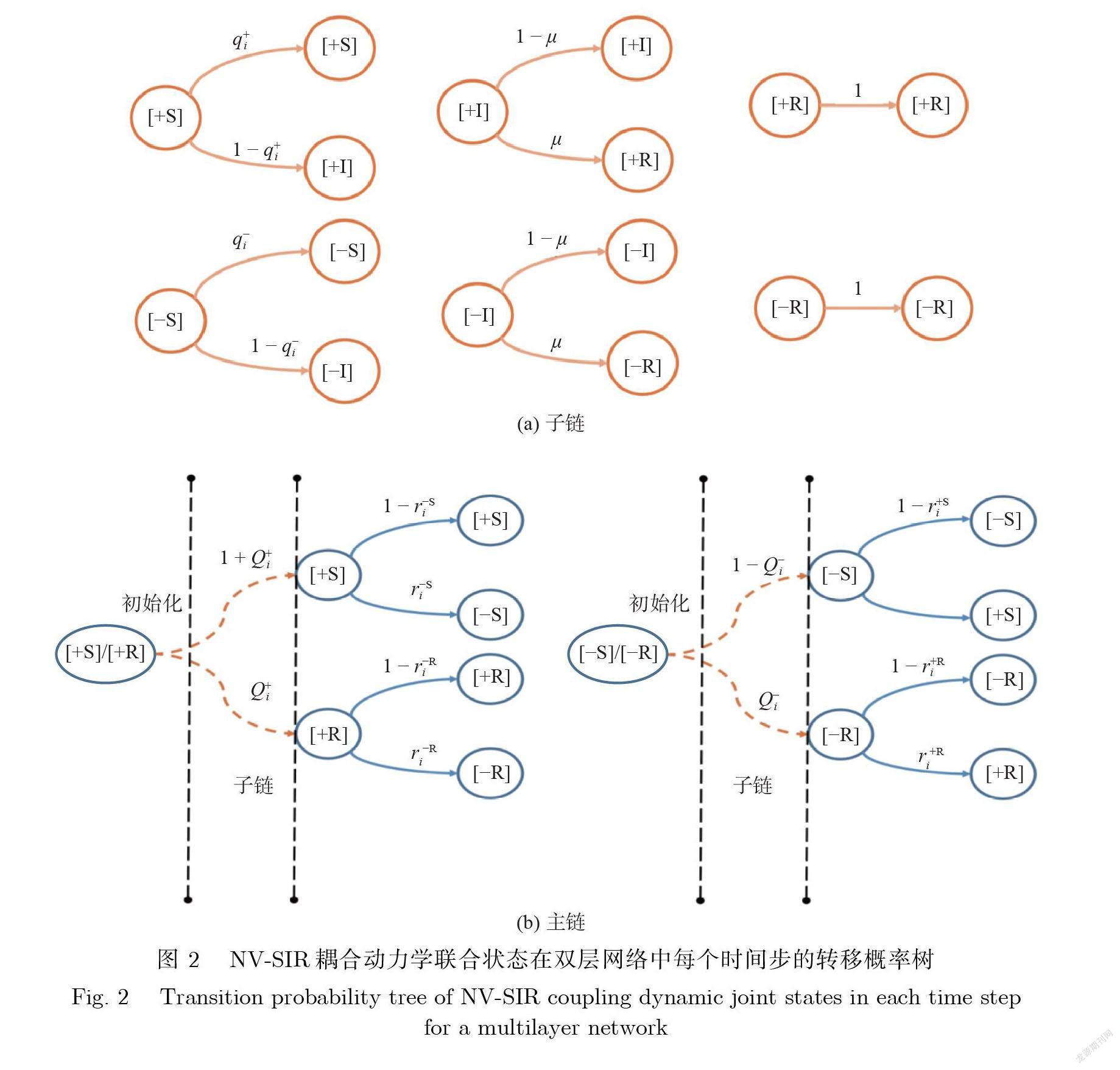
根据第1 章介绍的模型 ， 分别在投票层层面和信息层层面建立2 个微观状态马尔可夫链 ， 其中 ， 投票层是主链 ， 信息层是子链. 图 2所示为 NV-SIR 耦合动力学联合状态在双层网络中每个时间步的转移概率树. 下面分别讨论主链和子链的演化方程的构建过程.

2.1.1  微观马尔可夫链的子链方程

在信息层方面 ， 节点i 在 t 时刻可能处于子链中6 种联合状态中的某一种：持“+”意见并且不知道消息[+S];持“–”意见并且不知道消息[−S];持“+”意见并且活跃地传播消息[+I];持“–”意见并且活跃地传播消息[−I];持“+”意见并且传播过消息[+R];持 “– ”意见并且传播过消息[−R]. 用 Pi+S （t）、 Pi  S （t）、Pi+I （t）、 Pi  I （t）、Pi+R （t）、Pi  R （t）分別表示节点i 处于这6 种联合状态的概率 ， 同时使用状态转移概率树来描述子链中各个联合状态之间的转移路径 ， 如图2（a）所示.各个联合状态之间的转移概率方程：在 t 时刻持“+”意见的节点i 不被邻居说服传播消息的概率q （t）和持“–”意见不被其邻居说服的概率q i （t）. 方程具体为

（2）

其中 ， Pj（I） = Pj+I + P 利用方程（2）和图2（a）所示的方案 ， 可以为节点i 的耦合过程建立微观马尔可夫链的子链方程 ， 具体为

其中 ， τ是消息传播过程的时间尺度 ， 通常取τ→ +∞ ， 表示其远大于意见形成过程的演化速度.我们把在“+”意见和“–”意见影响下的消息传播过程演化至终态后 ， 节点 i 处于 R 状态的概率分别记为 Q （t）和Q i （t）.

2.1.2  微观马尔可夫链的主链方程

在投票层方面 ， 节点i 在 t 时刻可能处于主链中4 种联合状态中的某一种：持“+”意见并且不知道消息[+S];持“–”意见并且不知道消息[−S];持“+”意见并且传播过消息[+R];持“–”意见并且传播过消息[−R]. 用 Pi+S （t）、 Pi  S （t）、Pi+R （t）和Pi  R （t）分别表示节点i 处于这4 种联合状态的概率.各个联合状态之间的转移概率方程：节点 i 的联合状态[+S]→[−S]在 t 时刻的转移概率r iS （t）、[+R]→ [−R]的转移概率r iR （t）、[−S]→ [+S]的转移概率r S （t）和[−R]→ [+R]的转移概率r R （t）. 方程具体为

（4）

其中 ， Pj+ = Pj+S + Pj+R ; kA，i 表示节点 i 在 A 层的度值大小. 利用方程（2）− 方程（4）和图2（b）所示的方案， 我们可以为节点i 的耦合过程建立微观马尔可夫链的主链方程 ， 具体为

主链中的1次数值迭代相当于子链演化至终态（各个节点的状态概率不再发生变化）.值得注意的是 ， 每一次开启子链迭代时需要对信息层的节点状态进行初始化 ， 见图2（b）中的标注.随机地选取极少量种子节点作为初始传播者 ， 在概率上就表现为 ， 令网络中每个节点的 P 设定成极小的数值.

2.2  蒙特卡洛模拟实验

本文在模型蒙特卡洛模模拟实验过程中引入了稳态-终态动力学的多轮次方法[28-29]. 具体实验步骤如下.

1）首先 ， 初始化投票层节点的意见状态（通常是持“+”意见或“–”意见的节点数量各占5 成 ， 或者使某方占优势）.

2）然后 ， 在信息层上以投票层的意见共识为背景驱动消息传播过程.随机地选取极少量节点作为初始传播者 ， 其他的节点都是 S 状态. 每个时间步 S状态节点以βψi （t）的速率被它的 I状态邻居劝服 ， I 状态节点会以µ的速率恢复成 R 状态.

3）当信息层的传播过程抵达终态之后 ， 网络中将不会再存在 I状态节点.我们驱动投票层的意见形成过程 ， 该层每个节点的状态变化都会受到信息层的影响. 特别是 ， 投票层的节点在每个轮次至多改变一次意见（演化一步）.

4）重复执行步骤2）–步骤3）直至投票层和信息层的系统序参量稳定.由于“+”意见和“–”意见的对称性 ， 不妨设定：投票层的序参量为持“+”意见节点的比例;信息层的序参量为消息的最终传播规模， 即 R 状态节点的占比.

3  结果

为了验证本文提出的 MMCA 数值分析方法的准确性 ， 本文考虑了1 个规模 N =210的双层网络：投票层和信息层的拓扑结构均是无标度（Scale-Free， SF）[30]网络 ， 节点的度 d 是自然数 k 的概率为P （d = k）∝  ， 通常取γ= 3 ， 平均度⟨k⟩= 12 ， 将其称之为 SF-SF 双层网络. 为了不失一般性 ， 本文设定 ， 投票层的参数h =1 ， 信息层的消息传播过程的恢复速率µ= 1; 然后在这种大规模合成网络上对比 MMCA 数值分析和蒙特卡洛（MC）模拟实验的结果.在 MMCA 数值分析和 MC 模拟实验中 ， 设定双层网络演化的仿真步长均为0.01.

3.1  不连续相变向连续相变类型的转变以及多稳态区域的出现

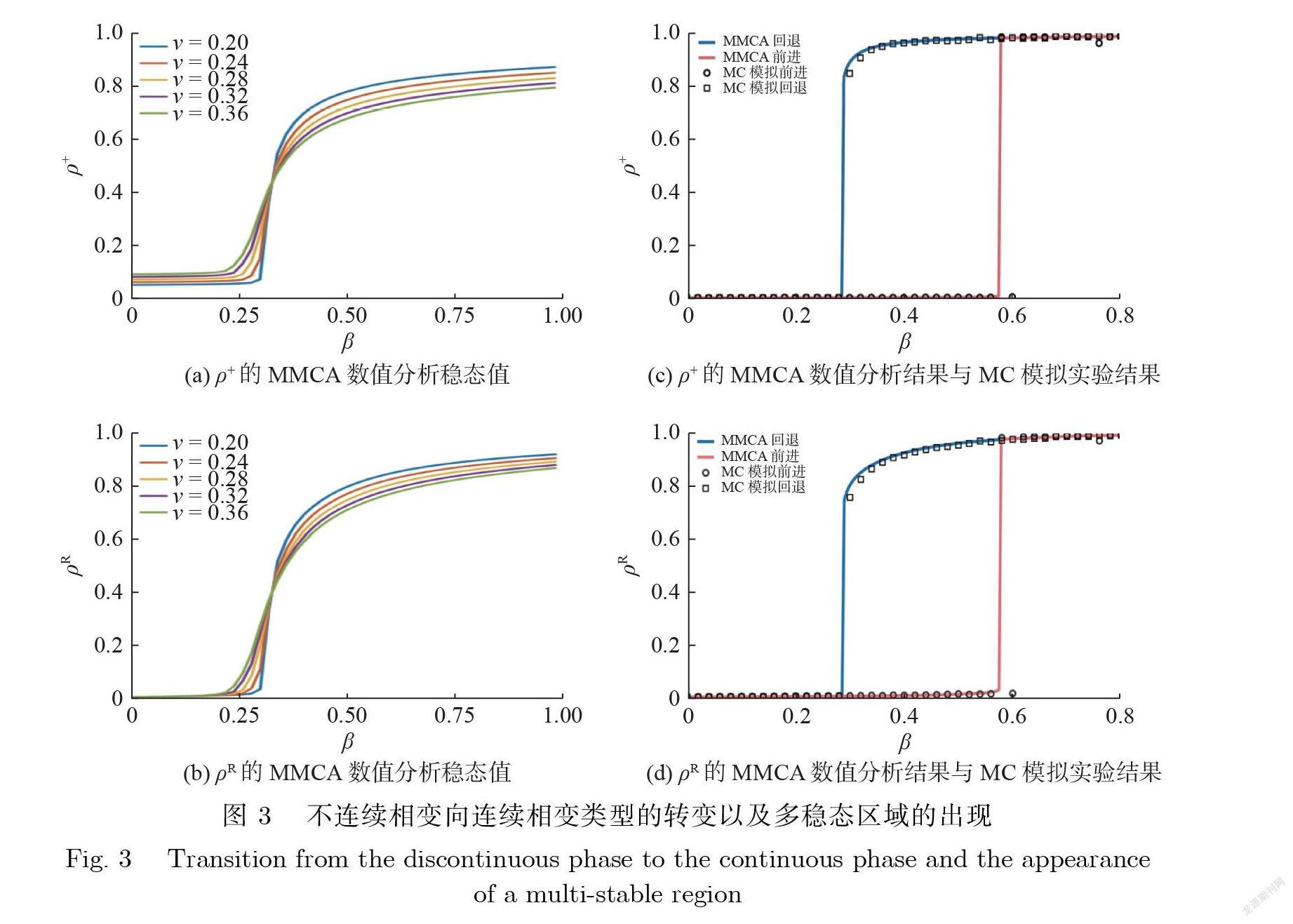
本文进一步研究了系统序参量作为β的函数随β增加的变化趋势 ， 结果见图 3. 图3（a）、图3（b）所示的是 ， 初始“+”意见个体比例为50%系统稳定时的“+”意见个体比例ρ+ =   Pi+和消息传播规模ρR =   P 的 MMCA 数值分析稳态值 ， 在不同意见形成过程的v 值条件下随β改变的趋势. 现在分别解释它们的物理意义：ρ+衡量的是在意见形成网络层中“+”意见在人群中的占比 ， 是社会舆论和民意最直观的体现;ρR 表示消息在人群中的最终传播范围 ， 该值越大消息的影响力就越广. 当v 值从0.20逐渐增加到0.36时 ， NV-SIR 耦合模型发生相变类型的转变：当v 值比较小的时候 ， 消息传播规模和“+”意见比例随着传播速率的变化发生不连续相变;当 v 值较大时 ， 2个动力学过程的序参量随传播速率的改变发生连续相变. 例如 ， 图 3（a）、图 3（b）中v =0.20时的线段 ， 消息传播规模和“+”意见比例在阈值βc = 0.3的左右两侧发生了不连续的跳变.

图 3（c）、图 3（d）也为不连续相变的发生提供了另一个强有力的证据：磁滞回线和双稳态现象.本文固定噪声为1 个较小的v =0.02 ， 然后对比了2 个序参量的 MMCA 数值分析结果（蓝色和红色线段）和 MC 模拟实验结果（黑色圆圈和方块散点）.通过从β= 0增加（红色线段和黑色圆圈散点）参数β ， 或从β= 1减少（蓝色线段和黑色方块散点）参数 b 来计算和模拟这些序参量的稳态值. 在过程实现中 ， 把当前参数β获得的稳态结果作为下一个参数β实验的初始条件（绝热近似方法）.本文发现 ， 伴随着不连续相变 ， 磁滞回线和多稳态现象出现了. 当系统的序参量处于比较高水平（低水平）的时候 ， 如果逐渐减少（增加）控制参数 ， 比如β ， 获得的2 条发生偏移的序参量曲线就是磁滞回线. 根据MMCA 数值分析结果和 MC 模拟实验结果， 发现以不同的β值作为出发点时（从β= 0增加或从β= 1减少）， 这些序参量的稳态曲线表现出磁滞回线的特征 ， 并且可能同时存在2种稳定的状态. 双稳态现象出现的原因：系统在较小噪声情况下 ， 投票层动力学的演化过程主要受信息层的影响. 比较高的初始“+ ”意见比例能增强信息层的传播过程 ， 更高的传播范围通过层间耦合作用的正反馈增强投票层“ +”意见共识的形成;相反 ， 较低的初始“+ ”意见比例可以抑制信息层的传播 ， 不利于投票层逐渐形成“+ ”意见共识. 从而 ， 较大（较小）的初始“+ ”意见比例将会导致不同的稳定状态. 因此 ， 在绝热近似的模拟过程中 ， 随着传播速率β的逐渐增大（向前）或減小（向后）， 不同的初始条件令系统在不同的临界点发生相变现象 ， 即产生了磁滞回线现象.在磁滞区域 ， 对应不同的β ， 系统会出现不同的稳态状态.

这意味着 ， 当社会意见共识的演化主要遵循“少数服从多数”的原则时 ， 系统的意见共识和消息影响范围会随着消息传播速率β的变化发生雪崩式级联反应;当意见共识过程主要依赖个体自发的随机改变意见这条原则时 ， 意见共识和消息影响范围在阈值附近随β缓慢且连续地变化.

3.2  MMCA 数值分析与 MC 模拟实验相图对比

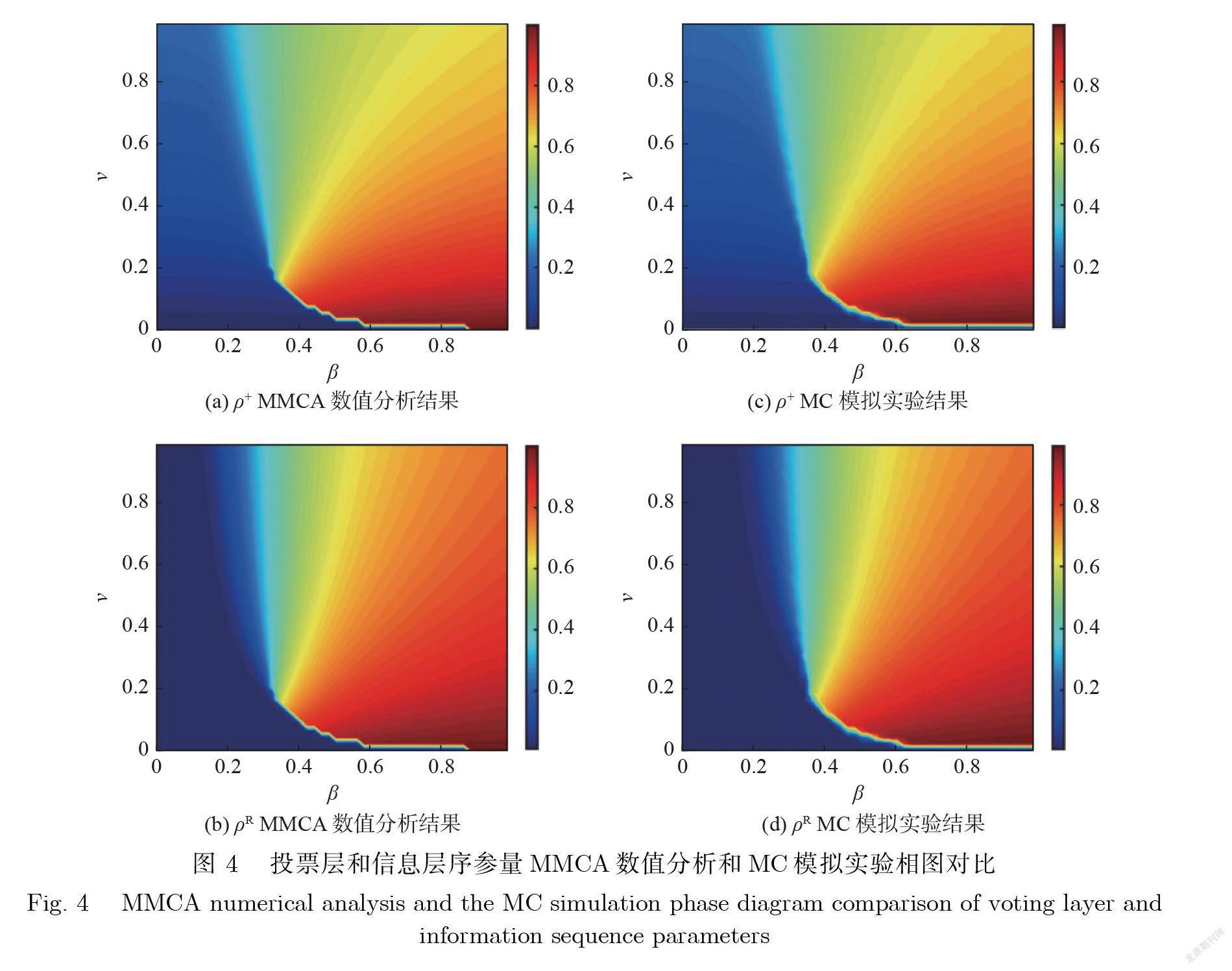
在图 4中 ， 绘制的是 MMCA 数值分析与 MC 模拟实验相图的对比 ， 分别考察了这两种系统序参量作为参数v 和参数β的函数 ， 其中 ， 图 4（a）、图 4（b）展示了 MMCA 数值分析的结果 ， 图 4（c）、图 4（d）展示了200次 MC 模拟实验的平均结果. 这两种系统序参量分别是 ， 在图 4（a）、图 4（c）中展示了持“ +”意见的节点比例ρ+ ， 在图 4（b）、图 4（d）中展示了消息传播规模ρR .通过从β =0 增加参数β 来计算和模拟这些序参量的稳态值.

MMCA 数值分析和 MC 模拟实验在整个相空间有很好的一致性 ， 相对误差小于2%.由图4 发现 ， 当 v 较小时 ， “+ ”意见节点比例ρ+ ， 一方面可能远高于50%并且造成全局“+”意见共识;另一方面可能接近0 从而造成“– ”意见全局共识 ， 是否全局“+ ”意见共识取决于传播速率β的大小.从β= 0增加参数β来计算和模拟这些序参量的稳态值时 ， 与较大噪声相比需要较大的β值才能使意见共识发生翻转. 当 v 较大时 ， 无论消息是否爆发 ， ρ+的值都在50%附近 ， 此时不存在明显的全局意见共识的倾向. 因此 ， 本文得出：意见形成过程的噪声较小时 ， 系统存在明显的全局意见共识 ， 无论是“+ ”意见还是“– ”意见;当噪声较大时 ， 全局意见共识的趋势并不明显 ， 因为“+ ”意见节点比例非常接近50%.

4  结论

人类社会中 ， 人群意见共识的形成过程和消息传播过程是相互影响的 ， 并且它们的时间演化尺度不同.基于双层网络 ， 本文构建了一个具有不同时间演化尺度的耦合传播模型—噪声投票-SIR 传播耦合模型. 本文发展了一套微观马尔可夫链数值分析方法来描述双层网络上的不同时间尺度耦合传播动力学过程. 通过在 SF-SF 双层网络上进行的大量蒙特卡洛模拟实验 ， 验证了本文所提出的 MMCA 数值分析方法的准确性. 本文研究发现 ， 噪声投票-SIR 传播耦合模型发生了相变类型的转变现象：当意见形成的噪声比较小的时候 ， 消息传播规模和“+”意见比例等序参量会随着传播速率的变化发生不连续相变 ， 并存在磁滞回线和双稳态现象;当噪声较大时 ， 2个动力学过程的序参量会随传播速率的改变而发生连续相变.

本文提出的分析框架可为不同时间演化尺度的相互耦合动力学系统的研究提供理论借鉴 ， 所获得的研究结果有助于人们对真实世界中人群意见共识形成过程与消息传播过程之间相互作用的了解.本文创新性：在结合实际物理场景和一定的假设的前提下 ， 将投票类动力学和疾病/消息传播类模型耦合起来 ， 建立了一个全新的双层耦合网络模型;根据实际场景 ， 考虑了两种动力学不同的时间演化尺度 ， 其相比此前大部分时间演化尺度一致的假设工作具有更强的现实意义. 更进一步 ， 展望未来的工作 ， 可以深入结合实际场景的真实数据 ， 通过挖掘意见形成过程和消息传播过程之间更深层次的相互影响机制 ， 从而构建出更为合理的耦合传播模型.

[參考文献]

[1]NEWMAN M E J. The structure and function of complex networks [J]. SIAM Review， 2003， 45（2）：167-256.

[2]PASTOR-SATORRAS R， VÁZQUEZ A， VESPIGNANI A. Dynamical and correlation properties of the Internet [J]. Physical Review Letters， 2001， 87（25）：258701.

[3]COHEN R， EREZ K， BEN-AVRAHAM D， et al. Resilience of the Internet to random breakdowns [J]. Physical Review Letters， 2000， 85（21）：4626-4268.

[4]GALLOS L K， COHEN R， ARGYRAKIS P， et al. Stability and topology of scale-free networks under attack and defense strategies [J]. Physical Review Letters， 2005， 94（18）：188701.

[5]DÖRFLER F， CHERTKOV M， BULLO F. Synchronization in complex oscillator networks and smart grids [J]. Proceedings of the National Academy of Sciences of the United States of America， 2013， 110（6）：2005-2010.

[6]SHAO J， HAVLIN S， STANLEY H E. Dynamic opinion model and invasion percolation [J]. Physical Review Letters， 2009， 103（1）：018701.

[7]PASTOR-SATORRAS R， CASTELLANO C， VAN MIEGHEM P， et al. Epidemic processes in complex networks [J]. Review of Modern Physics， 2015， 87（3）：120-131.

[8]KURANT M， THIRAN P. Layered complex networks [J]. Physical Review Letters， 2006， 96（13）：138701.

[9]MUCHA P J， RICHARDSON T， MACON K， et al. Community structure in time-dependent， multiscale， and multiplex networks [J]. Science， 2010， 328（5980）：876-878.

[10]SZELL  M，  LAMBIOTTE  R，  THURNER  S. Multirelational  organization  of large-scale  social  networks  in  an  online  world [J]. Proceedings of the National Academy of Sciences of the United States of America， 2010， 107（31）：13636-13641.

[11]BAXTER G J， DOROGOVTSEV S N， GOLTSEV A V， et al. Avalanche collapse of interdependent networks [J]. Physical ReviewLetters， 2012， 109（24）：248701.

[12] CAI W R， CHEN L， GHANBARNEJAD F， et al. Avalanche outbreaks emerging in cooperative contagions [J]. Nature Physics，2015（11）：936-940.

[13] SANZ J， XIA C Y， MELONI S， et al. Dynamics of interacting diseases [J]. Physical Review X， 2014， 4（4）：041005.

[14] DANZIGER M M， BONAMASSA I， BOCCALETTI S， et al. Dynamic interdependence and competition in multilayer networks [J].Nature Physics， 2019， 15（2）：178-185.

[15] NICOSIA V， SKARDAL P S， ARENAS A， et al. Collective phenomena emerging from the interactions between dynamical processes inmultiplex networks [J]. Physical Review Letters， 2017， 118（13）：138302.

[16] SORIANO-PAÑOS D， GUO Q T， LATORA V， et al. Explosive transitions induced by interdependent contagion-consensus dynamicsin multiplex networks [J]. Physical Review E， 2019， 99（6）：62311.

[17] PASTOR-SATORRAS R， VESPIGNANI A. Epidemic spreading in scale-free networks [J]. Physical Review Letters， 2001， 86（14）：3200-3203.

[18] NISHIKAwA T， MOTTER A E， LAI Y C， et al. Heterogeneity in oscillator networks： Are smaller worlds easier to synchronize？[J].Physical Review Letters， 2003， 91（1）：014101.

[19] GOMEZ-GARDENES J， MORENO Y， ARENAS A. Paths to synchronization on complex networks [J]. Physical Review Letters， 2007，98（3）：034101.

[20] VELÁSQUEZ-ROJAS  F，  VAZQUEZ  F. Interacting  opinion  and  disease  dynamics  in  multiplex  networks： Discontinuous  phasetransition and nonmonotonic consensus times [J]. Physical Review E， 2017， 95（5）：052315.

[21] BRODKA P， MUSIAL K， JANKOWSKI J. Interacting spreading processes in multilayer networks： A systematic review [J]. IEEEAccess， 2020， 8（1）：10316-10341.

[22] BOCCALETTI S， BIANCONI G， CRIADO R， et al. The structure and dynamics of multilayer networks [J]. Physics Reports， 2014，544（1）：1-122.

[23] CARRO A， TORAL R， SAN M M. The noisy voter model on complex networks [J]. Scientific Reports， 2016， 6（1）： Article number24775.

[24] SOOD V， REDNER S. Voter model on heterogeneous graphs [J]. Physical Review Letters， 2005， 94（17）：178701.

[25] MORENO Y， PASTOR-SATORRAS R， VESPIGNANI A， et al. Epidemic outbreaks in complex heterogeneous networks [J]. TheEuropean Physical Journal B： Condensed Matter and Complex Systems， 2001， 26（4）：521-529.

[26] CHAKRABARTI D， WANG Y， WANG C X， et al. Epidemic thresholds in real networks [J]. ACM Transactions on Information andSystem Security， 2008， 10（4）： Article number 13.

[27] GOMEZ S， ARENAS A， BORGE-HOLTHOEFER J， et al. Discrete-time Markov chain approach to contact-based disease spreading incomplex networks [J]. Europhysics Letters， 2010， 89（3）：038009.

[28] ZHANG H F， WU Z X， TANG M， et al. Effects of behavioral response and vaccination policy on epidemic spreading - an approachbased on evolutionary-game dynamics [J]. Scientific Reports， 2015（4）： Article number 5666.

[29] ZHANG H F， SHU P P， WANG Z， et al. Preferential imitation can invalidate targeted subsidy policies on seasonal-influenza diseases [J].Applied Mathematics and Computation， 2017， 294（1）：332-342.

[30] BARABASI A L， ALBERT R. Emergence of scaling in random networks [J]. Science， 1999， 286（5439）：509-512.

（責任编辑：李艺）