稀疏扫描型医用CT的快速成像算法开发

董 建，陈 昊，杨耿煌，丁 洋，杨晓霞，车艳秋

（1.天津职业技术师范大学天津市信息传感与智能控制重点实验室，天津 300222；2.天津职业技术师范大学工程实训中心，天津 300222）

此前的研究已经表明电离辐射存在致癌风险，且计算机断层扫描（computed tomography，CT）辐射已经被证明与癌症发病率增加有关[1]。临床上常通过减少CT扫描时设备旋转一周的投影视图数量或降低X射线管功率的方法来减少CT检查时的辐射暴露[2]。对于低剂量CT的图像重建可使用投影域预处理、迭代重建算法等方案[3]。对于投影数量不足的图像重建，常用的滤波反投影重建算法会不可避免地产生条状伪影[4]。而得益于压缩感知（compressed sensing，CS）理论的发展，针对稀疏投影或含噪声投影数据，采用压缩感知的方法进行图像重建，逐渐得到广泛的研究与论证[5]。该类算法可更准确地重建出细节保留完整、伪影分布较少的CT图像，能够满足人们对CT成像质量日渐提高的要求[6-7]。因此，基于压缩感知理论的CT图像重建算法开始被广泛研究和应用[8]。

压缩感知理论在图像重建领域中的应用框架是以由数据保真项和正则化项（惩罚因子）共同组成的代价函数为基础，利用凸函数最优化理论，通过对代价函数进行最小化而得到最优解。正则化项的设计对于求解该类欠定问题具有重要作用。压缩感知理论在此领域应用时与CT成像的相关性取决于CT图像是否稀疏，在压缩感知理论的正则化项设计中常用稀疏变换来实现图像的稀疏性。2006年Donoho在文献[5]中指出离散梯度变换和小波变换经常被用于对图像进行稀疏变换。目前常用的稀疏变换是对图像的全变分（total variation，TV）变换[9]。基于TV正则项的压缩感知算法被证明在图像的稀疏重建中具有良好的效果，且在CT图像重建领域表现出较强的噪声抑制特性[10]。文献[11]提出了全变分最小化的PICS（prior image compressed sensing）算法，利用先验图像约束的压缩感知来提升稀疏投影角度下的图像重建质量，但此类基于TV正则项的压缩感知算法在重建后仍存在伪影残留[12]。

研究发现导致在基于TV正则项的重建图像中出现潜在模糊结构和补丁状伪影的主要原因是TV正则项通过线性变换提高预恢复图像的稀疏性，此过程易过多考虑图像各像素之间的位置相关性而忽略图像边缘、图像纹理部分等灰度不相关像素间的过渡。为解决上述问题，本团队在2016年提出了基于非线性滤波的压缩感知重建算法理论。在进行稀疏变换时，原有的TV线性滤波方法被非线性滤波代替，经过实验得出基于此法的压缩感知算法在保留图像边缘和细节纹理及消除大块模糊上具有良好效果[13-14]。

此非线性压缩感知算法在图像重建中常进行上千次迭代以得到收敛图像，且单次迭代运算量大，运算时间长，导致此算法的收敛速度慢。本团队在2017年提出了基于非线性滤波器的压缩感知的加速算法，将代价函数拆分成若干个子函数并使用凸函数优化中近端优先理论，每次以行优先准则进行迭代[15]，此算法提高了收敛速度，使算法的可用性大幅提高。

非线性滤波压缩感知算法在对于恢复图像交错处细节和边缘信息以及抑制大块模糊方面具有良好效果，但经加速后单次迭代时间仍较长，收敛速度慢。研究发现，基于压缩感知算法的CT重建技术大多使用空间域滤波方法实现对重建图像稀疏化的过程。而滤波器的设计对图像重建质量和重建速度起着关键作用[16]。相对的频域滤波器特别是低通频域滤波器可去除图像的高频噪声等干扰，且对于平滑图像具有良好效果[17]。同时低通频域滤波过程中总体时间复杂度为O（n），远低于先前研究中所选取的非线性滤波器的时间复杂度O（n2）。在低通滤波器中，巴特沃斯低通滤波器对图像边缘的模糊程度大量减小，且没有振铃效应，可以在对图像噪声及伪影平滑过程中相对较多地保存图像边缘细节[18]。指数型低通滤波器具有更快的衰减特性且同样没有振铃效应[17]。

结合以上2种低通频域滤波器的特点，在原研究的基础上，用新的低通频域滤波器替代改进后的压缩感知重建加速算法中的非线性空间域滤波器进行实验。本文将通过使用基于低通滤波的压缩感知重建算法实现在相对较高地保留原可用等级的图像边缘和纹理细节的前提下，加快重建图像收敛速度，使基于此算法的CT图像重建技术可用性进一步提高。

1 本文算法

1.1 模型的建立

本研究的目的是利用稀疏角度的投影数据重建出临床可用的CT图像。此处对图像重建过程建立模型，将利用投影数据进行图像重建的问题转化为对方程组Ax=d的求解问题。其中，向量d=（d1，d2，…，dI）T为扫描得到的投影数据，x=（x1，x2，…，xJ）T为待重建的图像，A为一个I×J维度的系统矩阵，由CT器械决定。本文研究稀疏角度投影的重建问题，即d的维度I远小于x的维度J，因此基于该问题的数学模型可转化为求解欠定方程组的问题[19]。基于压缩感知理论建立代价函数

式中：L（x）为数据保真项；U（x）为正则化项。

L（x）由每次重建时投影数据的估计值与CT扫描时投影数据真实值的最小二乘差来限定，表示为。系统矩阵A在任务执行中表示对待重建图像x的取投影操作。正则化项U（x）代表对图像的稀疏变换。将代价函数进行展开表示

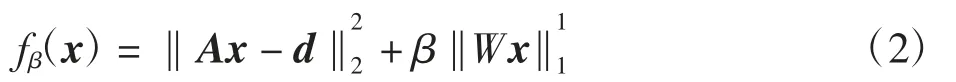
式中：β为用来控制正则化项作用强弱的超参数，亦起到限定运算过程中不发生过拟合的作用；W为对向量x的稀疏化操作，即提取图像的高频信息，将x转换为稀疏向量。

式中：I为单位算子；L操作表示对图像的空间域平滑滤波。

因此，可将代价函数进一步表达为

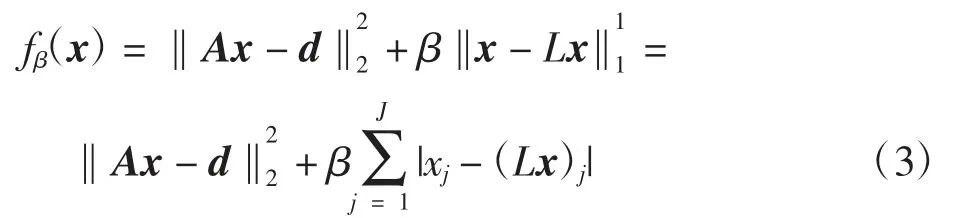
1.2 正则化项中的频域滤波

基于压缩感知算法的CT重建技术大多使用空间域滤波方法来实现图像稀疏化的过程，且团队以往的研究发现基于空间域的NL-median（NonLocal-median）滤波器在重建图像过程中可以高质量地恢复待重建图像，但收敛速度过于缓慢[21]。本文的创新点在于将既往研究的空间域滤波升级为低时间复杂度的低通频域滤波，主要验证了巴特沃斯低通滤波器和指数型低通滤波器被嵌入正则化项后的工作机制。巴特沃斯低通频率滤波器和指数型低通频域滤波器的传递函数分别由式（4）、（5）定义，为了更好地描述频率域处理机制，使用二维矩阵来代表图像。

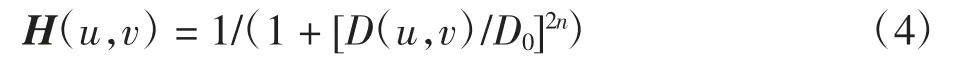
式中：u，v为频率变量；D（u，v）为坐标到中心点的欧式距离；D0为巴特沃斯低通滤波器的滤波半径；n为滤波器的阶数，视实验条件确定。

由于改用低通滤波器后算法滤波过程是对图像频域信息进行操作，在滤波开始前需将由数据保真项限定后的图像信息通过傅里叶变换从空间域变换为频率域，离散图像f（x，y）用式（6）实现傅里叶变换。

式中：M为图像的行像素数；N为图像的列像素数。

对于变换后的图像在频域中实部和虚部的值分别进行基于式（4）和式（5）的滤波运算，将得到的滤波后的图像的频域值进行如式（7）所示的傅里叶逆变换。由此完成正则化中的稀疏变换过程。

综上所述，基于频域滤波的压缩感知在稀疏角度CT图像重建中的代价函数为

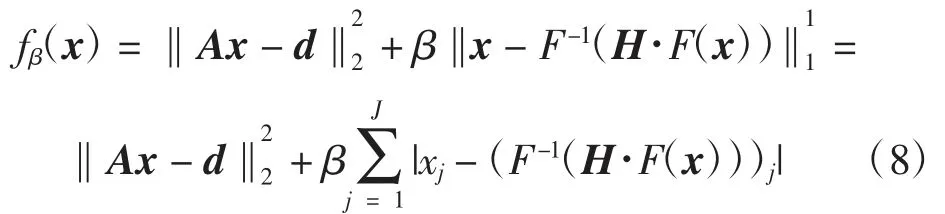
式中：F和F-1分别为图像的傅里叶正变换与逆变换；H为低通频域滤波操作。

1.3 近端分裂理论

实施算法推导前，有必要先对其基础内容的近端分裂理论及其对算法推导的重大贡献做简要介绍。首先考虑以下凸优化问题

假定式中f（x）为可能不可微分的下半连续凸函数。近端算子法（proximal operator）为求解此类最优化问题提供了解决方案。对应于f（x）的近端算子表达式为

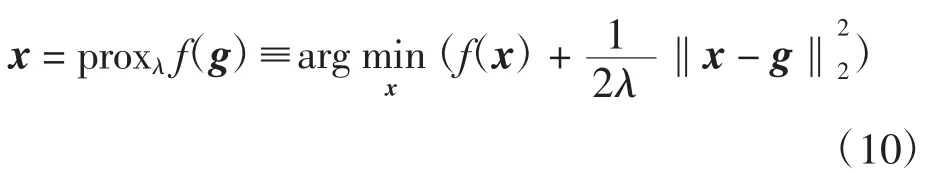
式中：λ为步长参数。

近端算子具备2种优秀属性：①其可针对任何一个下半连续凸函数进行定义，即使该函数不可微（如L1范数）；②在步长参数λ＞0的前提下，满足x=proxλf（g）的定点x与使凸函数f（x）取最小值时的变量x相一致。这2个性质可以应用迭代式求得凸函数f（x）取得最小值时的变量x

式中：k为迭代次数。

该迭代算法叫做近端最小化算法，其为不可微凸函数的最优化问题提供了强有力的解决方案。

凸函数f（x）可拆分成若干分量函数fi（x），即，其中，fi（x）（i=1，2，…，I）均为可能不可微，但满足下半连续的凸函数。此时，假定凸函数的近端算子求解难度巨大，而其各个分量函数fi（x）的近端算子能够由低计算成本求得。近端分裂理论能够为该条件下的凸优化问题提供良好解决方案，其处理方式为在求解由x(k)到x(k+1)的过程中，进一步将问题分解为按照i=1，2，…，I的顺序进行各分量函数所对应的近端算子的计算，即

式中：当i=I时，x(k+1)=x(k，i+1)；k为主循环变量；i为子循环变量。步长参数λ(k)值随k值改变。为了使所求解序列x(k)收敛于函数f（x）取最小值时的变量x，λ(k)需满足如下条件

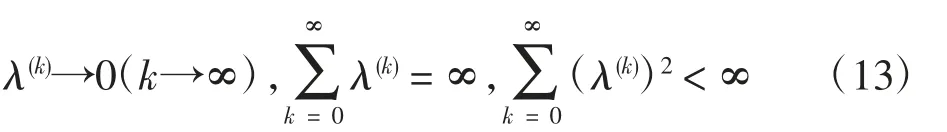
近端分裂理论为本文L1范数重建算法的构建提供了理论依据。

1.4 算法实现过程

为了进一步加快算法的运算速度，基于近端算子和近端分裂理论将系统矩阵按行进行拆分。依据近端分裂理论，代价函数式（8）可表示为

式中：g（x）为正则化项；fi（x）为数据保真项。

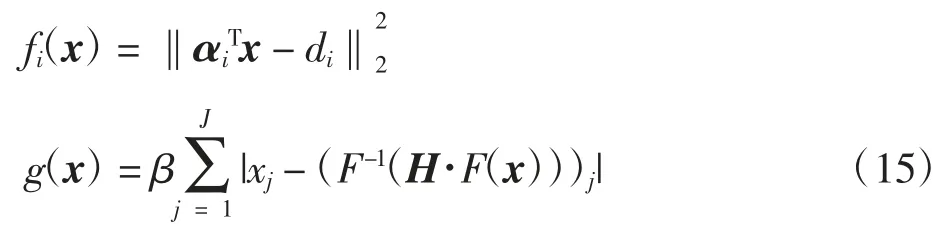
式中：I为所测得投影数据的维数；αi为对应的系统矩阵A的第i个向量；αiT为向量αi的转置。

对于数据保真项，由于此算法在迭代时以行更新，可参考ART（algebraic reconstruction technique）算法加速中使用随机顺序行更新法实现对本算法数据保真项的求解加速[22]。对于正则化项，此处引入跨度参数S，使在数据保真项求解的主循环中以S为跨度进行I/S次滤波，S的最优取值视实验条件确定。数据保真项的行迭代过程如下

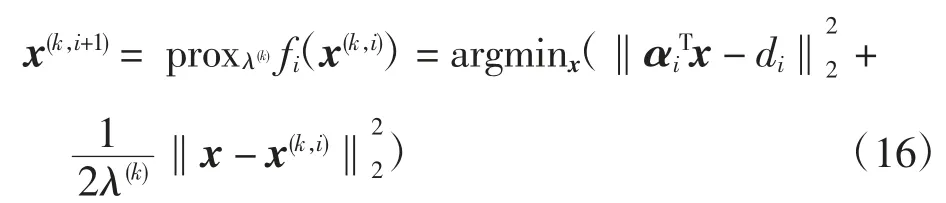
式中：proxλ(k)fi（x(k，i)）为近端算子运算；λ(k)为迭代时的步长参数；k为主迭代因子。为了避免数据陷入极限环，令λ(k)=λ(0)/（1+ε·k），λ(0)和ε取值依具体任务确定；i为每次计算数据保真项时的行迭代因子。

通过对保真项求解可得

对正则化项g（x）进行prox算子展开如下

在迭代求解过程中，当λ(k)取值足够小时，x无限接近已知量x(k，i+1)，因此在λ(k)取值足够小的前提下，H·F（x）可由当前图像的滤波结果H·F（x(k，i+1)）代替。因此，式（18）的求解过程可由式（19）的固定形式的软阈值更新实现。

至此完成了本文中提出的重建算法的构建。基于频域滤波的压缩感知应用于稀疏扫描CT图像重建的算法总结如下：

输 入 像素数为N×M的投影数据d。

初始化 设置步长参数的控制变量λ(0)，ε，设置β＞0的超参数以及S＞0的跨度参数。

步骤1 赋值总循环次数k=0，像素数为N×N的初始图像x(0)=0。

步骤2 计算步长参数λ(k)=λ(0)/（1+ε·k），令x(k，0)=x(k)。

步骤3 图像更新程序

傅里叶正变换，求得F（x(k，i+1)）；低通频域滤波处理，求得H·F（x(k，i+1)）；傅里叶逆变换，求得F-1（H·F（x(k，i+1)）），并赋值x(k，i+1)←F-1（H·F（x(k，i+1)））。

for（j=0；j＜N*N；j++）do

式（19）软阈值处理。

步骤4 令x(k+1，0)=x(k，I)，返回步骤2。

输 出 当循环条件被满足，输出图像x(k+1)。

实验中发现将非线性滤波器用低通频域率滤波器替代后，重建图像的收敛速度显著提升，但重建图像中有放射状伪影未被去除。由此根据此前重建算法的研究，在上述算法的基础上，加入微弱的TV正则化项用于去除重建图像中的放射状伪影。代价函数式升级为式（20）。诸如式（20）双正则化项的代价函数的最优化及算法推导与前述推导方法类似，在文献[21]中有详细论述。

式中：γ为用来控制TV项作用强弱的超参数；‖x‖TV为对图像进行TV最小化。

本研究中限定取值足够小，即让TV项起到微小的辅助作用，旨在有效利用TV项在图像处理中对噪声的抑制作用。被定义为TV范数，其可看作是一种特殊的L1范数，即灰度梯度的L1范数，用于去除重建图像中的放射状伪影。

2 实验结果与分析

在本文实验设计中选用口腔CT平扫影像，该影像牙齿、牙槽骨面积大且与其他组织的射线吸收系数差异较大，在图像重建过程中易在高亮部位产生放射状伪影，此外牙齿形状及排列方式的细节丰富，因此可采用此影像来对比新旧算法重建效果。本实验采用图像如图1所示，像素为512×512，图像CT值（hounsfield unit，HU）最小处为-1 000，最大处3 071，由此可较准确地反映图像中不同部位的对比度差异。

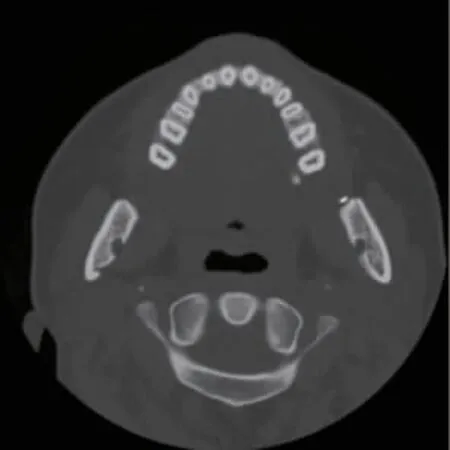
图1 人体口腔CT平扫图像

本研究分别对图1从180°中以间隔为2取90个角度的投影数据，间隔为3取60个角度的投影数据以及间隔为4取45个角度的投影数据模拟真实情况下的稀疏角度的CT扫描过程。以模拟投影数据为输入进行基于NL-median和巴特沃斯低通频域滤波器、指数型低通频域滤波器压缩感知图像重建对比实验。

2.1 重建结果对比展示

针对新算法中使用的巴特沃斯低通滤波器和指数型低通滤波器的参数D0和n的选择进行如下实验：以90个角度的投影数据以及巴特沃斯低通滤波器为例，固定参数n=10，分别设置D0=1、D0=400与D0=500进行重建实验，对比发现D0的最佳取值位于1～500，经过实验得到其最佳取值为400。固定D0=400，分别设置n=1、n=10与n=100进行重建实验，对比发现n的最佳取值位于1～100，经实验得到其最佳取值为10。90个角度投影数据不同频域滤波参数重建对比图像如图2所示，基于45、60、90个投影数量的不同正则化项的压缩感知重建算法的重建图像结果如图3所示。

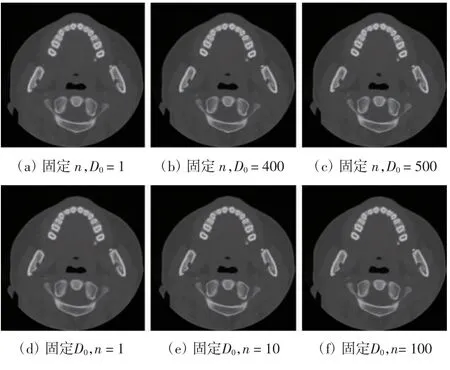
图2 90个角度投影数据不同频域滤波参数重建对比图像

图3 基于不用滤波器不同投影数量的压缩感知重建图像

图3（a）、（b）、（c）从左至右依次是依据45个、60个、90个投影角度正弦图的重建结果。

在本实验的重建过程中，对于不同的正则化项选取同样的共同参数：λ(0)=0.2，ε=1，β=1 200，S=4。图3所展示的重建图像是分别迭代100次后得到的重建结果。在图3（a）的实验中，对于NL-median滤波器设置的搜索窗口和滤波窗口分别为7×7和5×5，设置δ1=10，δ2=10 000。基于此，重建的图像边缘比较清晰，细节恢复比较完整。在图3（b）的实验中，对于巴特沃斯滤波器设定滤波半径D0=400，传递函数中参数n=10，同时在迭代100次的前60次为了消除重建图像的放射状伪影加入γ=2的TV正则化项。基于此，重建的图像同样可以观测到，重建图像边缘较清晰，细节较完整。在图3（c）的实验中，将指数型低通滤波器滤波半径设为D0=400，传递函数中参数n=10，在迭代100次的前60次为了消除重建图像的放射状伪影加入γ=2的TV正则化项。基于此，重建的图像可以观测到同上述巴特沃斯频域滤波器有类似的效果。

2.2 重建图像及算法的客观评价

为了更好地评价基于不同滤波器的CS算法在重建后得到的收敛图像的质量优劣，引入了平均绝对误差（mean absolute deviation，MAD）作为评价指标。MAD的运算公式为

式中：J为图像像素个数，在本实验中取值512×512；xj为每次运算后得到的图像的各个像素的CT值；Xj为原始图像，即图1中各像素的CT值。在此评价体系中MAD的值越小，最终的收敛图像相较于原图的重建质量越好，同时用最终收敛时间来评价各个算法执行图像重建任务的可用性。上述各算法分别以45个、60个、90个投影角度迭代100次后的收敛图像的各评价指标数值如表1所示。

表1 以45、60、90个投影角度重建图像的评价指标

为了更精确地比较重建图像与原始图像的CT值，重建图像与原图第256行像素CT值的拟合曲线如图4所示。

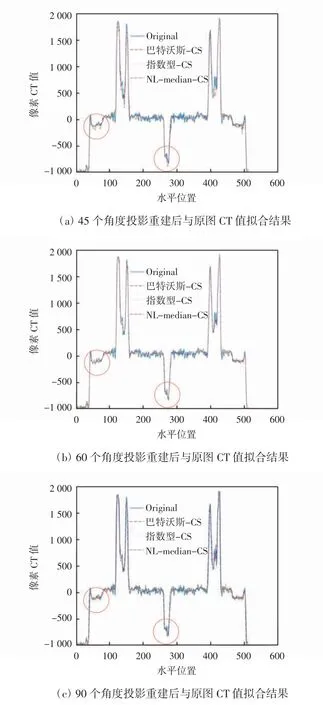
图4 重建图像与原图第256行像素CT值的拟合曲线

图4（a）、（b）、（c）分别给出了基于45个、60个、90个角度的投影数据重建后的第256行的各个像素的CT值与原始图像CT值的拟合情况。从图4（a）、（b）可知，在以45个、60个角度的投影数据重建后，基于巴特沃斯和指数型滤波的CS重建算法与NLmedian-CS在对图像恢复上均在图像边缘跳变处有冲激，在图像过渡平缓的区域拟合效果良好。从图4（b）、（c）可知，红色标注处所示的当投影数据达到60个、90个角度时，基于巴特沃斯和指数型滤波的CS重建算法的图像在图片CT值突变冲激处比原图像的拟合效果有很大改善。

3 结语

本研究为了进一步提高基于稀疏投影数据的图像重建算法的可用性，对之前提出的NL-median-CS算法中的正则化项在稀疏化时的滤波器进行了重新选择，基于新型频域滤波器的压缩感知算法在稀疏投影重建时亦可保持较高图像质量。由实验结果可知，图像细节纹理、边缘信息可相对完整地保留，且基于新滤波器的CS算法在迭代速度上有了显著提高，大幅降低了收敛时间。实验结果显示，相同迭代次数下基于新滤波器的CS算法的迭代时间约是先前的基于NL-median滤波器的1/10，显著增强了该算法的可用性。在本文提出的基于新滤波器的CS算法中仍有较多参数需要最优化，且为了获得较好的重建效果常需要繁杂的参数训练过程，该过程不利于算法鲁棒性的提升。同时，从整体上看，非线性压缩感知重建算法在重建中获得收敛图像的速度仍与正在CT中使用的FBP算法有较大差距。使算法中各参数可根据不同部位的CT图像自适应改变是本团队下一步研究的主要方向。本文所提出新的基于频域滤波的压缩感知CT图像重建算法显著提高了图像的重建速度，且较好地保证了图像质量，具有一定的实际应用价值。