剪切波变换和条纹方向二值掩膜的相位解包裹方法

李碧原，赵鑫春，张 军，王 宇

（天津职业技术师范大学电子工程学院，天津 300222）

条纹投影轮廓术（fringe projection profilometry，FPP）是一种非接触、快速且精度高的三维形貌测量方法，被广泛地应用于光学三维测量领域[1]。在FPP三维测量中，待测物理量与编码在条纹中的相位信息直接相关，准确地提取相位是FPP三维测量的关键。目前，傅里叶变换轮廓术[2]和相移轮廓术[3]是两类最常用的相位提取方法，这两类方法均利用反正切函数求解相位，导致相位值分布在[-π，π]之间且存在2π的相位跳变，这种相位分布称为包裹相位。而真实相位φ和包裹相位φ之间的存在关系：φ=φ+2πK，-π≤φ≤π，即真实相位与包裹相位之间存在2π整数倍的相位差，从包裹相位中恢复出真实相位的过程称为相位解包裹。

目前，相位解包裹方法主要分为时间相位解包裹方法和空间相位解包裹方法2类。时间相位解包裹方法每一个像素点的相位值都是独立计算的，从而有效地减少了解包裹误差的传递。Zuo等[4]对时间相位解包裹方法做了综述性研究，并比较分析了时间相位解包裹中常用的多频法、多波长法和数论相位解包裹方法的性能。与时间相位解包裹方法相比，空间相位解包裹算法只需要一幅包裹相位图即可获得解包裹相位。空间相位解包裹方法可以分为2类：路径跟踪法和最小范数法。

路径跟踪法主要包括枝切法（branch cut）[5]、质量图引导相位解包裹法（quality guide phase unwrapping，QGPU）[6]、区域生长算法[7]、遗传法[8]和最小不连续法[9]。上述方法的区别在于如何设置积分路径对包裹相位梯度进行积分。基于最小范数的全局相位展开是一种与路径无关的相位解包裹方法。作为目前应用最广泛的全局相位解包裹方法之一，加权最小二乘相位解包裹方法（weighted least square method，WLSM）[10-13]已经被国内外专家学者研究多年。在WLSM中，加权系数的设定是最关键的一步，因为它决定了是否能够准确地区分出相位的不一致区域。近年来，针对WLSM加权系数的设定，相关专家学者提出了许多新方法：Ghiglia等[10]利用相关图作为加权系数。hen等[11]利用小波脊作为加权系数。Lu等[12]利用导数相关二值掩模图作为加权系数。Wang等[13]利用区域的可靠性图来定义加权系数。在条纹投影轮廓术实际应用中，由于高度剧烈变化、空间孤立的表面或图像光强度的突然变化，经常会遇到不连续的条纹和阴影。在这种情况下，相邻像素点之间的相位差可能会超过2π，条纹也会因为阴影而失去级次。

不连续条件下的相位展开仍然是一个具有挑战性的问题。近年来，学者们提出了一些解决不连续相位展开问题的方法。Rivera等[14]提出了一种基于鲁棒半二次正则化的通用正则化公式，用于处理带有噪声和相位不连续的相位解包裹问题。文献[15]提出了一种基于残差的质量导向相位解包裹方法。Zhao等[16]提出了一种snake模型辅助的质量导向相位解包裹方法。该方法利用梯度向量场snake模型对窗口傅里叶变换得到的质量图进行修改。在一些不连续的实例中，使用snake模型得到的高质量的图像比直接使用基于窗傅里叶变换的方法获得了更好的展开效果。Wang等[17]提出了一个完整的不连续条纹图处理流程。该方法利用基于局部方位相干的条纹分割方法和基于边界感知的相干增强扩散方法得到了质量图。文献[18]提出了一种新的加权最小二乘法，在该方法中加权系数是由反向导数方差相关图的二值掩模得到。Yan等[19]提出基于模糊集理论的自适应掩模生成算法并结合最小二乘法实现相位解包裹。

最近，深度学习算法也被引入到光条纹图相位解包裹领域，文献[20]提出基于深度学习的相位解包裹方法，该方法利用卷积神经网络对FPP条纹图中的周期顺序进行解码，解决了FPP中真实相位信息评估时的模糊性问题。文献[21]提出了基于聚类和卷积神经网络的二维相位解包裹网络结构“PhaseNet”。文献[22]提出基于卷积神经网络的时域相位解包裹方法。文献[23]提出一对多深度学习框架实现三步相移进而完成相位解包裹。文献[24]提出新的端到端的网络模型“H-Net”，通过引入全局指导路径提高了网络学习性能，实现了条纹结构光三维形貌测量。基于深度学习的相位解包裹方法能够处理多幅图像，但需要仔细地制作相应的训练集。

本文基于剪切波变换和条纹方向性提出一种新的加权最小二乘相位解包裹方法，该方法利用剪切波变换提取条纹，利用条纹方向性获取二值掩膜进而定义新的加权系数，该加权系数可以准确地区分包裹相位图中连续区域和不连续区域。将提出的新方法应用到模拟和实验获得的条纹投影静态和动态测量过程中，并与5种常用的相位解包裹方法进行比较。

1 单幅FPP条纹图相位提取和加权最小二乘相位解包裹

1.1 单幅条纹图的FPP相位提取技术

在FPP相位提取方法中，基于单幅FPP条纹图的相位提取方法以其速度快、适应性强和设备要求低等优点得到了广泛的应用。图1给出了基于单幅条纹图的FPP相位提取的主要流程，包括：①投影条纹的设计、②系统标定、③图像预处理、④条纹图去背景、⑤相位提取、⑥相位解包裹。

图1 单幅FPP条纹图相位提取流程图

该方法仅利用一幅FPP条纹图通过一系列的条纹分析方法便可以实现三维形貌的测量与显示。利用摄影机采集到的变形FPP条纹图的光强表达式为

式中：Ia为图像的背景；Ib（x，y）cos（φ（x，y）+2πf0x）为图像的条纹部分Ifringe；NOISE为噪声；φ（x，y）为相位信息；2πf0x为载频。

在单幅FPP条纹图三维形貌还原过程中，首先要利用计算机生成光栅条纹并利用投影仪投射到被测物体表面。这里的光栅条纹的设计可以按照实际需求进行调整。系统标定的目的是用于标定好整个测量系统中参数之间的关系，如标定摄影机与投影仪光心之间的距离，摄影机焦距等。图像预处理用于减少摄像机采集到的图像中由于环境等因素引起的噪声干扰；条纹图去背景是为了从条纹图中将有用的条纹信息从背景、噪声中分离开；相位提取和相位解包裹用于从变形条纹图中提取相位主值以及将相位主值连续化。

1.2 加权最小二乘相位解包裹方法

加权最小二乘相位解包裹方法（weighted least square phase unwrapping，WLSPU）的基本思想是计算解包裹相位差与包裹相位差的最小二阶范数，从而获得解包裹相位。

WLSPU的目标函数为

式中：φi，j为解包裹后的真实相位；Δφxi，j和Δφyi，j分别为包裹相位φi，j在x和y方向上的包裹相位差；wxi，j和wyi，j分别为包裹相位φi，j在x和y方向上的权重；M×N为包裹相位图的尺寸。

式中：wi，j为包裹相位图中每一点的加权系数。

从式（2）和式（3）中可以看出，在WLSPU中，最终解包裹的精度取决于加权系数的选择。在通常情况下，加权系数是由包裹相位图的质量图进行二值化计算得来的，将质量图中可靠区域的权重系数设为1，不可靠区域的权重系数设为0[13]。加权系数的一般表达式为

式中：qij为质量图；Γ为预先设定的阈值。

根据式（4）获得的加权系数，式（2）可以化简成求解Neumann边界条件下的泊松方程，等价于如下离散形式的泊松方程解

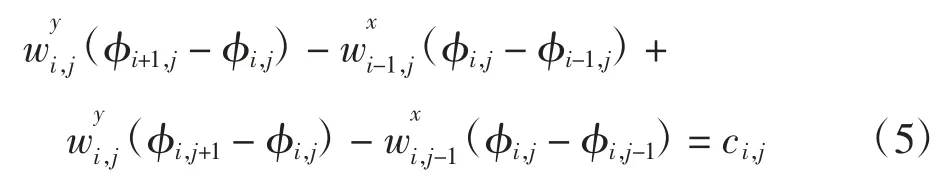
其中，加权相位拉普拉斯算子ci，j为

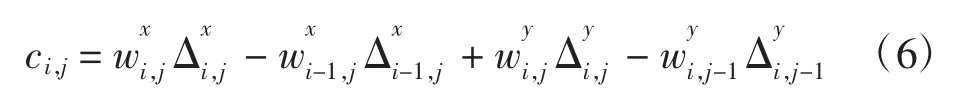
将式（5）改写成矩阵形式为

式中：Q为加权拉普拉斯算子；c为加权拉普拉斯操作向量；φ为解包裹相位向量；Q=P+D，P为非加权拉普拉斯算子，D为差异矩阵。

式（7）可以利用离散余弦变换法（discrete cosine transform，DCT）和预条件共轭梯度法（preconditioned conjugate gradient，PCG）来求解。

从式（2）到式（7）以及对加权最小二乘相位解包裹方法的描述可知，二值的加权系数可以准确地反映相位质量。WLSPU的精度取决于加权系数的选择。

2 加权系数计算方法

基于剪切波变换和条纹方向二值掩膜的加权系数计算方法，首先对FPP条纹图进行剪切波变换，利用剪切波变换去背景的同时获取条纹部分。然后计算条纹部分的方向一致性，通过设置阈值生成二值掩膜图，将二值掩膜图作为加权系数输入到加权最小二乘相位解包裹方法中实现精确的相位解包裹。

2.1 单幅FPP条纹图剪切波变换

文献[25]中提出了基于剪切波变换的FPP条纹图去背景方法，与傅里叶方法相似，提出的剪切波变换也利用图像的背景、噪声和条纹的频率在频域内不同来实现条纹图像去背景，但剪切波变换以其各向异性、方向的敏感性以及局部多尺度细分的优势更加适合于条纹分析。因此，相比于傅里叶变换，剪切波变换可以实现更精确的FPP条纹图背景和噪声的剔除，避免影响后续计算精度。基于剪切波变换的背景去除方法的步骤如下：

步骤1对式（1）中描述的FPP条纹图进行剪切波正变换，得到剪切变换相关系数

式中：SH为对图像进行剪切波变换；SHI为图像的剪切波变换系数。

步骤2对得到的剪切波变换相关系数进行硬阈值操作，去除低频分量

式中：shrink为硬阈值操作；δ为阈值。

阈值参数的选择与小波变换的方式类似，小波系数的阈值与图像中的噪声水平成比例。

阈值δ为

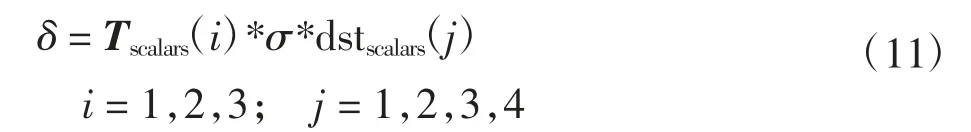
式中：Tscalars（i）为1×3的向量；Tscalars（1）是低通系数的阈值标量；Tscalars（2）是带通系数的阈值标量；Tscalars（3）是高通系数的阈值标量；*为卷积运算；σ为噪音的标准偏差；dstscalars（j）为包含标准偏差为1变换系数的高斯白噪声单元阵列，用来估计噪声级标度，尺度参数j=1，2，3，4。

步骤3进行剪切波逆变换得到FPP条纹图的条纹部分Ifringe

利用剪切波变换去除FPP条纹图的背景分量和噪声，得到了精确的条纹部分，接下来利用条纹部分获取加权系数。

2.2 计算条纹部分的方向二值掩膜

FPP条纹图是一种明显的方向流场，具有强烈的方向性。条纹方向相对于条纹的灰度或者梯度信息而言，是一个变化缓慢的信息量，其方向信息代表了图像的重要特征，因此可以用条纹图的方向信息来指导相位解包裹。

方向一致性是指条纹图像中某一区域内条纹方向的一致程度，方向一致性可以定义为

式中：Direction（i，j）和Direction（k，l）分别为在尺寸W×W的窗口中，中心像素（i，j）与其窗口邻域内其他像素点（k，l）的方向角。

从式（13）可以看出，对于条纹方向一致的区域，中心点的方向角Direction（i，j）与其周围邻域内像素点的方向角Direction（k，l）接近，所以条纹的连续区域的方向一致性是一个比较大的值。相反，在条纹不连续区域中，中心点的方向角Direction（i，j）与其周围邻域内像素点的方向角Direction（i，j）差距较大，所以不连续区域的方向一致性是一个比较小的值。

设置适当的阈值将一致性图转化成二值掩模图，将一致性大的点设为1，将一致性小的点设为0。

式中：TC为预先设定的阈值。

式（13）中涉及条纹方向角的计算，这里选用傅里叶法来计算条纹方向角，中心点（i，j）的方向角可以表示为

式中：E（ωk，ωl）为窗口的傅里叶功率谱；θk，l=tan-1（k，l）。

2.3 加权最小二乘相位解包裹

在获取新的加权系数之后，将加权系数带入到加权最小二乘相位解包裹算法中实现高精度的相位解包裹。具体步骤为：①利用剪切波变换将单幅FPP条纹图去背景，并获得条纹部分Ifringe；②依据式（15）计算条纹的方向图Direction（Ifringe）；③依据式（13）计算条纹的方向一致性Coherence（Ifringe）；④依据式（14）将一致性图转化为加权系数二值掩膜图Weight（i，j）；⑤将加权系数带入到式（2）中实现相位解包裹。基于剪切波变换和条纹方向二值掩膜的加权最小二乘相位解包裹方法可以对物体表面带有不连续性的包裹相位图实现准确的相位解包裹。

3 实验结果与讨论

文中提出基于剪切波变换和条纹方向二值掩膜的加权系数计算方法，利用该加权系数与加权最小二乘相位解包裹方法结合，可以对表面带有不连续性的包裹相位图实现准确的相位解包裹。将提出的方法应用到模拟和实验获得的FPP测量的相位解包裹中，并与非加权最小二乘法[10]（unweighted least square method，ULSM）、窗傅里叶质量导向相位解包裹方法[26]（window fourier quality guide phase unwrapping method，WFQGPUM）、窗傅里叶脊变换质量导向相位解包裹方法[27]（window fourier ridge quality guide phase unwrapping method，WFR-QGPUM）、Goldstein枝切法[5]、图切割法[28]（PUMA）进行比较。本文方法处理高度分布变化剧烈的FPP条纹图如图2所示。

图2 本文方法处理高度分布变化剧烈的FPP条纹图

图2（a）给出了一幅模拟FPP条纹图，图2（a）的生成公式由式（1）给出，其中噪声为高斯噪声，方差为0.3，相位值计算公式为

从图2（a）中可以明显看出，物体表面的高度分布变化剧烈。图2（b）给出利用剪切波变换对图2（a）移除背景图后的条纹部分，图2（c）给出利用提出的方法从图2（b）中获得的加权系数图，图2（d）表示包裹相位图。

理论相位和6种方法的解包裹相位图如图3所示。图3（a）—（f）给出了理论三维相位图和利用6种方法对图2（d）解包裹后的三维相位图。

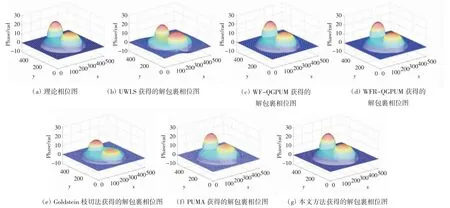
图3 理论相位和6种方法的解包裹相位图

此外，为了定量评估6种方法的性能，这里利用均方根误差（root mean square error，RMSE）作为评价指标来评估6种方法相位解包裹后的准确性。表1给出了6种方法的RMSE值，表2给出了图3中6种方法解包裹所用的计算时间。RMSE可以被定义为

表1 6种方法的RMSE

表2 6种方法对图2（d）解包裹所用的计算时间

式中：φi为解包裹相位值；φi*为理论相位值。

从表1中可以看到，本文方法的RMSE比PUMA方法更小。从表2中显示的计算时间看，PUMA方法的运算时间最长，计算效率较低。从图3中可以看出，非加权最小二乘法无法有效地识别出不连续区域，导致相位解包裹时的不准确。利用窗傅里叶和窗傅里叶脊方法获得的解包裹相位得到了充分的平滑，有效地抑制了噪声。Goldstein枝切法和PUMA图切割法不具有抑制噪声的能力，利用这2种方法获得的解包裹相位视觉效果较差。本文提出的基于剪切波变换和条纹二值掩膜的相位解包裹方法，无论从噪声抑制角度还是视觉效果都取得了令人满意的结果。

用实验获得FPP条纹图作为测试图像来测试本文提出的方法，FPP条纹图测试本文提出的方法结果对比如图4所示。图4（a）为实验获得的塑料人脸面具FPP条纹图，图4（b）为利用剪切波变换获得的条纹部分，图4（c）为利用条纹二值掩膜法获得的加权系数，图4（d）为包裹相位图。

从图4（c）中可以明显看出，利用本文方法得到的权重图能够识别出物体表面上的不连续区域。如人脸面具中的眼睛，嘴唇部分。图5给出6种方法对图4（d）的相位解包裹的结果，6种方法的计算时间如表3所示。

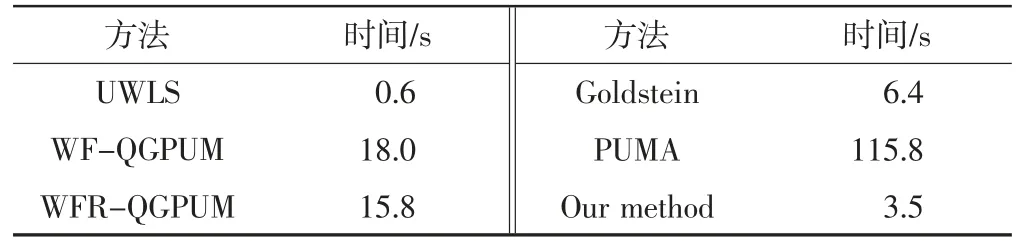
表3 6种方法对图5（d）解包裹所用计算时间

图4 实验获取的FPP条纹图和包裹相位图

图5 6种方法的解包裹结果

从图5可以看出，利用非加权最小二乘法和Goldstein枝切法获得的解包裹相位图视觉效果较差。窗傅里叶和窗傅里叶脊方法在人脸面具的边缘处的解包裹效果不够理想。PUMA方法在人脸面具顶部区域受到了噪声的干扰。从表3中发现PUMA方法计算效率较低，本文方法能够有效地识别不连续区域避免误差传递。此外，本文方法在保证精度的情况下计算时间较少。

4 结语

本文提出了一种新的加权最小二乘相位解包裹方法，该方法的主要优点是利用剪切波变换和条纹二值掩膜准确地区分包裹相位图中不连续区域和连续区域。此外，采用模拟图和实验图对提出的方法进行测试，并与5种常用的相位解包裹方法进行比较。实验结果表明：本文提出的方法精度高且计算速度较快，能够有效地识别不连续区域，避免相位解包裹时的误差传递。