光纤陀螺冗余可修复系统可靠性评估

杨茜茜， 耿丽松， 张 宇

(中国飞行试验研究院，陕西 西安 710089)

0 引 言

光纤陀螺作为新型角速率传感器，可以为飞行器提供准确的角速度、角位移和方位等关键参数，完成对飞行器运动轨迹与姿态的把控[1]，是飞行试验领域的一类关键传感设备。故需光纤陀螺具备高稳定性和高可靠性。在光纤陀螺自身可靠性提升空间较为有限的情况下，提升惯性测量系统可靠性的常用方法是对组成该系统的光纤陀螺应用冗余技术[2]。冗余是使器件或系统获取高可靠性、高稳定性和长寿命的有效技术之一，其核心思想是利用低可靠性元器件相互备用构成较高可性的系统[3]。当组成系统的某一元器件失效时，可以隔离故障，切换到冗余部分代替失效部分继续运行，只有当规定的基础元器件均失效时系统才会发生故障，进而提高系统可靠性[4]。由多台光纤陀螺冗余组成的惯性测量单元是飞行器等复杂可修装备的关键部件，是一种结构精密的可修系统。如果其发生故障则会对装备功能发挥产生重大影响，甚至造成灾难。因此快速准确地评估和分析其可靠性，准确掌握系统的实际性能，对降低系统风险、提高飞机、导弹等装备任务成功率有重要意义。

国内外对冗余系统可靠性已有研究，如郄朝辉等[5]采用马可夫链定量求解了多组件冗余系统可靠性。尹行等[6]考虑了组成系统元器件失效率之间的相依性，分析了冗余系统可靠性。文献[7-9]基于系统冗余关系建立联了故障树模型。但通过故障树图，仅仅可以直观地从中了解顶事件、中间事件与底事件间的逻辑关系。若需对光纤陀螺冗余系统进行更深入的研究还需采用其他方法求解故障树模型。传统的故障树求解方法如上行法、下行法和二元决策图法等采取不交化处理存在计算量会随系统规模呈指数增长的问题，对整个故障树模型求解相对繁杂且低效。蒙特卡洛仿真法通过对底设备失效时间进行抽样来模拟系统运行情况，可以直接实现故障树的定量分析而不需要繁复而费时的最小割集和结构函数求解过程，因此蒙特卡洛方法可以更为快捷有效地对故障树进行定量分析处理。

飞行试验领域，光纤陀螺可靠性评估是近年来才面对的一个新课题，目前的研究也大多集中于将光纤陀螺视为不可维修器件的情况[10]，对于光纤陀螺冗余可修复系统可靠性问题鲜有研究。若不加以区分直接套用不可修系统的可靠性评估模型及方法，就不能准确描述光纤陀螺冗余系统可修复性在可靠性评估结果中的体现，研究结果也难以作为光纤陀螺设计、研制阶段的指导。故亟需开展光纤陀螺冗余可修复系统可靠性评估工作。

1 冗余系统可靠性评估整体思路

本文采用故障树和蒙特卡洛仿真两者相结合的方法。基于光纤陀螺冗余系统逻辑结构建立故障树模型，采用蒙特卡洛仿真法求解光纤陀螺冗余系统的可靠性指标。流程图如图1所示，整体实施步骤如下：

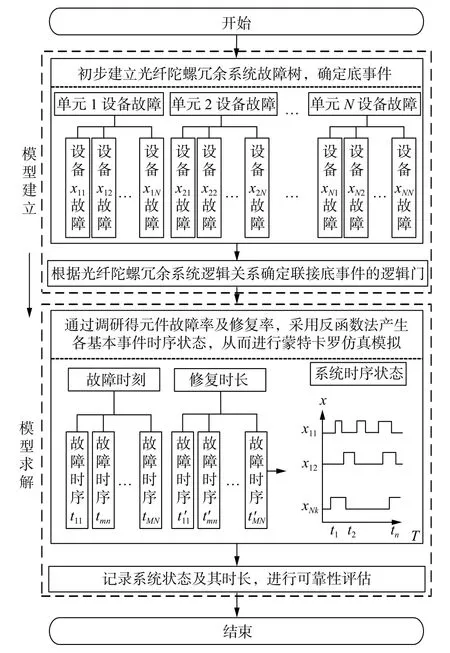
图1 光纤陀螺可靠性评估步骤

1）建立光纤陀螺冗余系统故障树：通过分析组成各个单元模块中光纤陀螺的失效情况，基于系统逻辑及其时序特性，建立光冗余系统故障树模型。

2）确定故障树底事件：各个光纤陀螺发生故障失效为故障树基本底事产生随机数数列，采用逆函数方式算法代入基本事件的故障分布函数和修复分布函数，抽取修复时间。

3）蒙特卡洛仿真：通过MATLAB编程，模拟各个基本事件的时序状态，计算得出每次仿真中光纤陀螺冗余系统各个时刻的故障状态并统计仿真后的相关数据，实现对光纤陀螺冗余系统的可靠性定量求解。

2 光纤陀螺冗余系统可靠性模型

2.1 系统冗余关系

将单个光纤陀螺按三维空间中指定方向安装，即可测得此方向的实时角速率，从而计算角位移。在飞行试验中，为了测得飞机在滚转、俯仰和偏航3个方向的角速率参数，一般在这3个相互垂直的方向各安装一台陀螺，构成一个惯性测量单元。在飞行试验领域，要求惯性测量单元具有可靠性高、寿命长等特点，除了从光纤陀螺的光路电路设计、元器件选型和外壳材质等方面来提高光纤陀螺自身可靠性之外，还需对构成惯性测量系统的测量单元进行备用冗余，甚至还需对构成惯性测量单元的光纤陀螺进行备用冗余。

如图2所示，本文分析对象由两组相互独立的惯性测量单元IMU1和IMU2组成，这两组惯性测量单元互为备用，即当且仅当IMU1和IMU2同时发生故障时，整个光纤陀螺冗余系统故障。在IMU1中，4个光纤陀螺分别沿空间坐标轴的X、Y、Z方向和体对角线S方向安装构成测量单元IMU1。同样，在IMU2中，另外4个光纤陀螺分别沿X′、Y′、Z′和S′方向安装构成测量单元IMU2，安装在每个测量单元内部体对角线方向的光纤陀螺作为X、Y、Z三个方向的备用，当这三个方向中某一方向的光纤陀螺失效时，对角线方向的陀螺可以作为该失效方向陀螺的备用投入工作，这种情况下测量单元仍能正常工作。但当每一测量单元中失效陀螺数量≥2时，该测量单元发生故障无法工作。

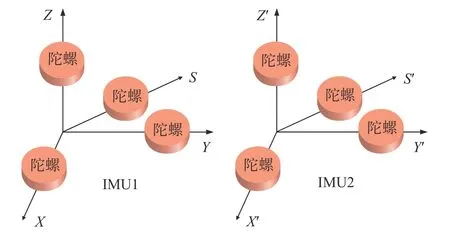
图2 光纤陀螺惯性测量单元冗余系统示意图

2.2 光纤陀螺冗余系统FTA模型

故障树分析（FTA）是一种直观建立复杂冗余系统可靠性模型的有效方法[11]，它不仅减少了分析元件数目，而且避免了对故障重复搜索。

本文建立的光纤陀螺冗余系统故障树如图3所示，以“系统故障”为顶事件，以“IMU1故障”和“IMU2故障”为中间事件，光纤陀螺G1～G8故障为底事件。底事件符号及其对应事件如表1所示。两个中间事件同时发生则导致顶事件发生，故选择逻辑门“与”门联接两个中间事件。事件“IMU1故障”包含4个底事件G1～G4，同样，事件“IMU2故障”包含4个底事件G5～G8，在每个中间事件中，有两个或超过两个底事件发生则该中间事件发生，故采用四选二门。

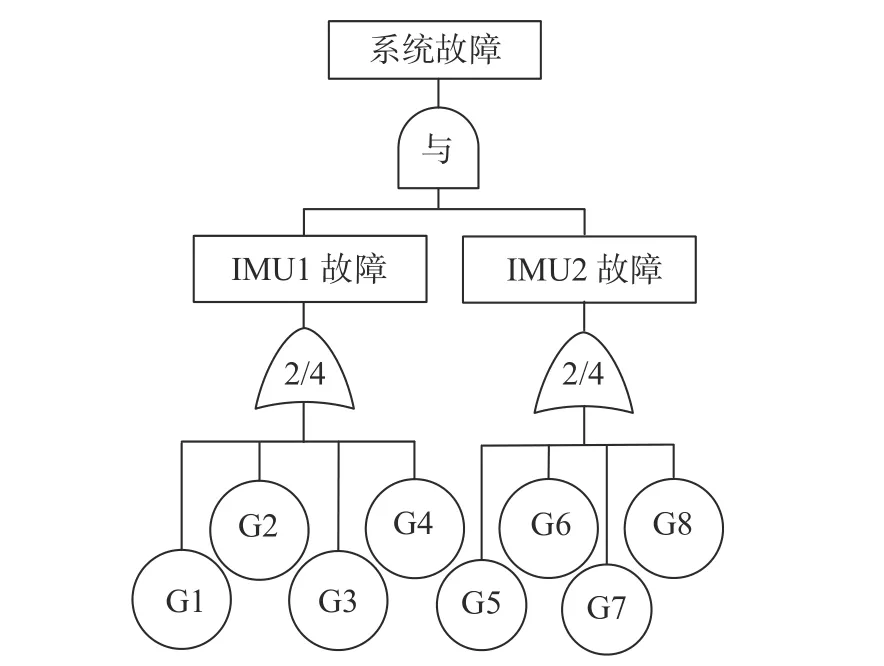
图3 光纤陀螺冗余系统故障树模型

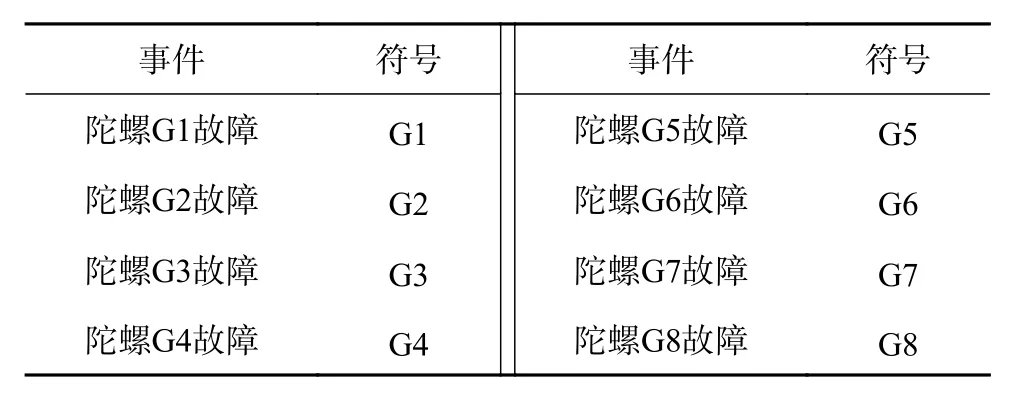
表1 FTA底事件及其对应符号

2.3 可靠性指标定义

光纤陀螺可靠性评估指标一般可用时间和概率表示[12]，常用的指标包括平均无故障工作时间（mean time between failure，MTBF）、平均故障修复时间（mean time to repair，MTTR）、稳态可用度A及稳态不可用度A′等，文献[12]具体定义上述指标及其计算方法。

MTTR指光纤陀螺从故障发生到修复时间的期望值，可表示为：

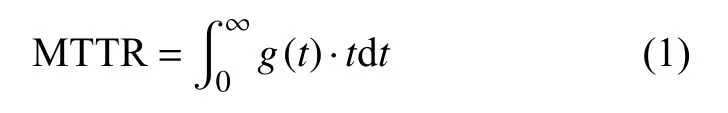
其中g(t)表示陀螺的修复密度。

MTBF是陀螺无故障工作时间的数学期望值，公示表示如下：

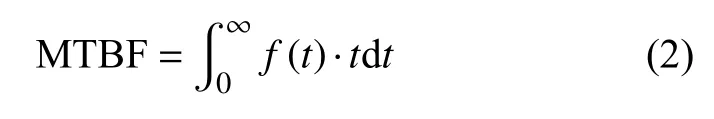
其中f(t)为陀螺在(t,t+Δt]间首次发生故障的概率，即失效密度。

可用度A(t)指在光纤陀螺0时刻正常工作，且至t时刻也能正常工作的概率。特别地，当陀螺故障率及修复率服从指数分布，可用度A(∞)收敛于一个常数，定义其为稳态可用度A，公式表达如下：

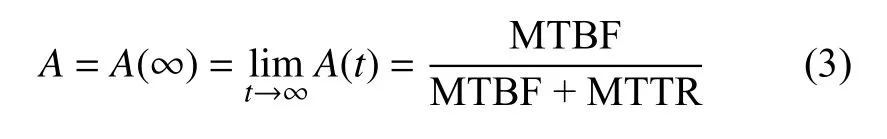
相对应的，稳态不可用度A′为：

特别地，当系统故障及修复服从指数分布，稳态不可用度可表示为：

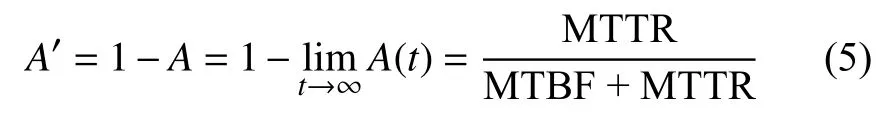
3 光纤陀螺冗余系统可靠性模型求解

3.1 蒙特卡洛仿真法

蒙特卡洛法按一定的步骤模拟随机出现的各种系统状态，利用MATLAB工具箱里随机数发生器产生一组符合该系统模型的随机数，生成足够多的抽样样本，用这些随机数来代替工程样本数据，从多次仿真结果中得到系统较为丰富可靠性指标，适应性较高，说服力强，大大提高了计算效率[13]。

图4展示了两元件组成的串并联系统时序状态转移过程。每个元件分别包含正常运行和故障修复两个状态，对各元件当前所处状态的持续时间进行抽样，记录所有元件的时序状态转移过程，得到元件1运行时长为T11,T12,···,T1M，故障修复时长为T′11,T′12,···,T′1M，元件 2 运行时长为T21,T22,···,T2M，故障修复时长为T′21,T′22,···,T′2M。组合所有元件的时序状态转移过程，如：0～t3时刻，元件1运行状态持续时长为T11，故障修复状态持续时长为T′11，元件2运行状态持续时长为T21，故障修复状态持续时长为T′21。状态组合后，对串联系统而言，0～t1时刻，两元件均处于运行状态，系统正常；对并联系统而言，0～t3时刻，两元件中，其一处于运行状态，则系统正常，两元件同处于故障修复状态，则系统故障。以此类推，得到直至tM时刻的串并联系统时序状态。对抽样获得的系统所有状态进行分析，计算系统的可靠性指标。

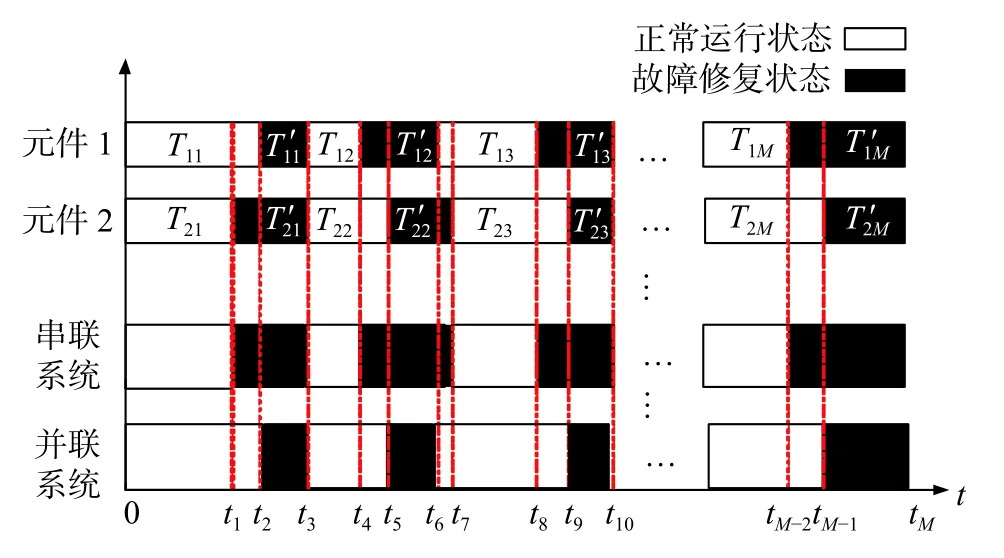
图4 串并联系统时序状态转移过程

3.2 算法描述及指标计算

采用蒙特卡洛法对光纤陀螺惯性测量单元冗余系统故障树模型进行求解计算，图5为考虑陀螺修复性的蒙特卡洛算法流程，其变量定义和算法描述如下：

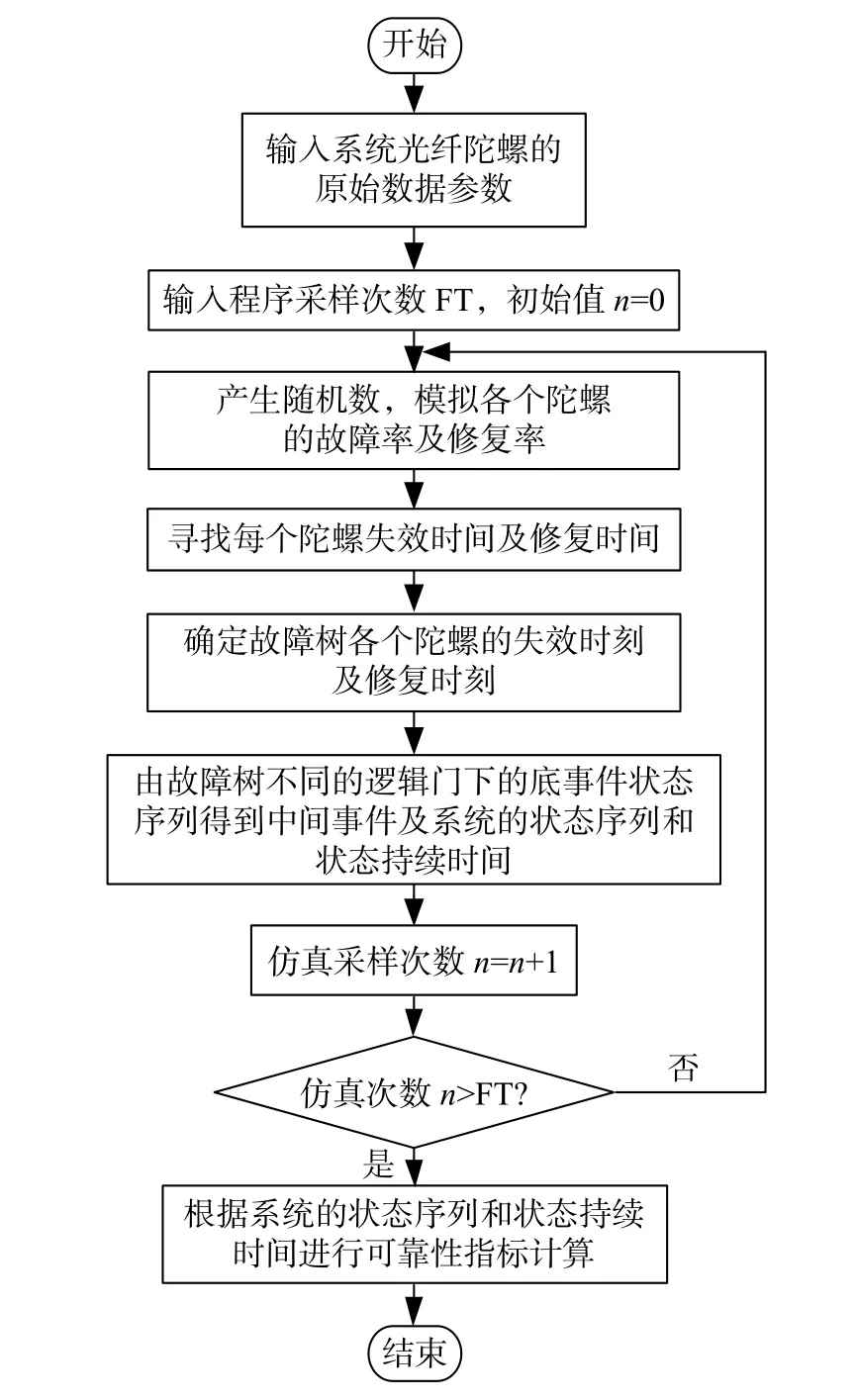
图5 考虑时变故障率的序贯蒙特卡洛算法流程

1）参数输入。设置8个光纤陀螺故障率rc1～rc8及修复率uc1～uc8；设置仿真抽样次数FT，受计算机硬件及MATLAB约束，有取值上限。

2）随机数产生。产生随机列sjs1～sjs16，每一数列包含FT个随机数。

3）抽样得到光纤陀螺失效时间和修复时间。基于产生的随机数，采用反函数法得到8个光纤陀螺的失效时间STc1～STc8和修复时间XTc1～XTc8（此处假设失效率和修复率服从指数分布），则对于光纤陀螺G1有：

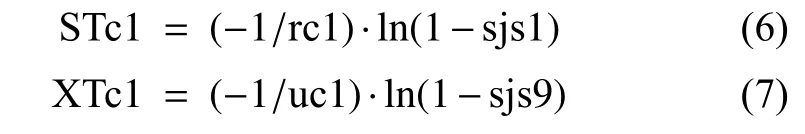
4）陀螺状态标记及时间标记揉合。运行状态标记为0，失效状态标记为1，修复状态标记为2，按抽样所得的陀螺状态改变时刻进行时间排序。

5）中间事件失效逻辑判断。根据故障树中的逻辑门即或门、与门和选择门得到每个惯性测量单元IMU1和IMU2的时序状态。

6）各个测量单元故障、修复时刻提取。基于步骤5）中惯性测量单元IMU1和IMU2的失效时刻和修复时刻, 按其状态改变时刻进行时间排序，提取得到各个单元状态转换时刻。

7）顶事件失效逻辑判断。根据故障树中联接中间事件的逻辑门得到整个光纤陀螺惯性测量单元冗余系统的时序状态，并记录系统故障总次数NS和修复次数NX。

8）系统故障、修复时刻提取。基于步骤7）中整个光纤陀螺惯性测量单元冗余系统的失效时刻TS和修复时刻TX, 按其状态改变时刻进行时间排序，提取得到系统状态转换时刻。

9）可靠性指标计算。通过仿真统计，计算得到平均修复时间MTTR、平均无故障工作时间MTBF、稳态可用度A和稳态不可用度A′。

4 实例分析

4.1 基础数据

光纤陀螺可靠性研究大多默认其故障及修复服从指数分布，即光纤陀螺故障率和修复率均为常数[12]，本文参考文献[14]采用光纤陀螺失效率为5.855 4×10-6次/h，表2列举了实际工程中光纤陀螺在4种不同维修类型情况下的平均修复时间和平均维修率，其中修复率为修复时间的倒数[13]。一般可认为在同一个光纤陀螺冗余系统中，同型号陀螺故障率相同，修复率相同。

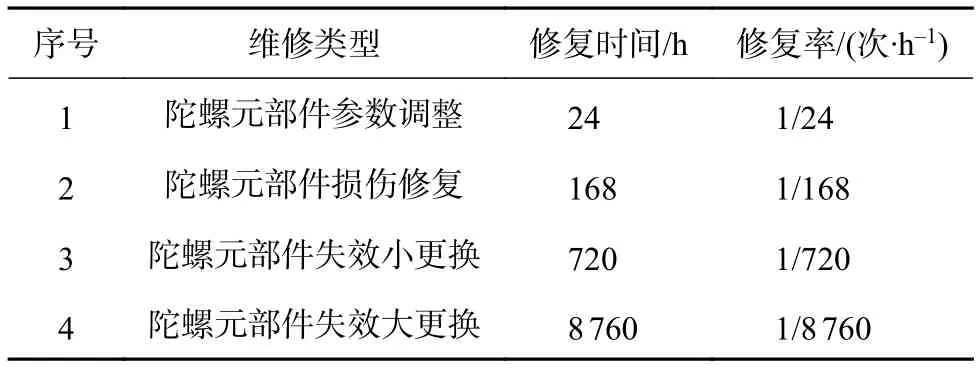
表2 光纤陀螺不同维修类型下的修复率估计

4.2 光纤陀螺冗余系统可靠性指标计算

图6直观记录了光纤陀螺在4种不同修复类型下整个冗余系统的稳态不可用度曲线。经100 000次仿真抽样后，计算得到维修类型1（元部件参数调整）情况下的系统稳态不可用度均大致趋于2.6×10-7，维修类型2（元部件损伤修复）情况下的系统稳态不可用度均大致趋于8×10-6，维修类型3（元部件失效小更换）情况下的系统稳态不可用度均大致趋于1.43×10-4，维修类型4（元部件失效大更换）情况下的系统稳态不可用度均大致趋于1.75×10-2。

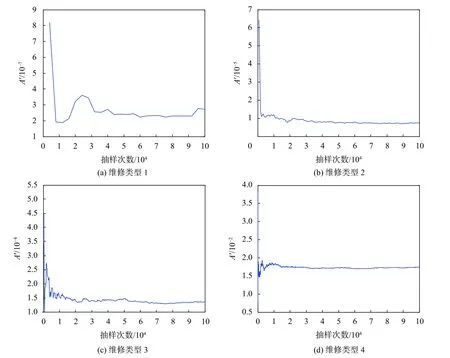
图6 光纤陀螺冗余系统稳态不可用度图

为验证本文所提故障树结合蒙特卡洛（FTA-蒙特卡洛）方法的可用性，突出方法优势。在维修类型4中，即当陀螺修复率为1/8 764 次/h时，比较图7中的传统蒙特卡洛与FTA-蒙特卡洛稳态不可用度指标结果，可见两种方法下指标的结果差异性不大，表明故障树结合蒙特卡洛的可靠性评估方法能够胜任光纤陀螺冗余可修系统的可靠性评估任务。考虑到该系统实时产生的海量数据，算法的收敛速度与稳定性是需要考虑的因素，由两种算法的曲线可知，相较于传统蒙特卡洛法，FTA-蒙特卡洛法的收敛速度更快、稳定性更强、所需的计算能力要求较低，适用性更广。

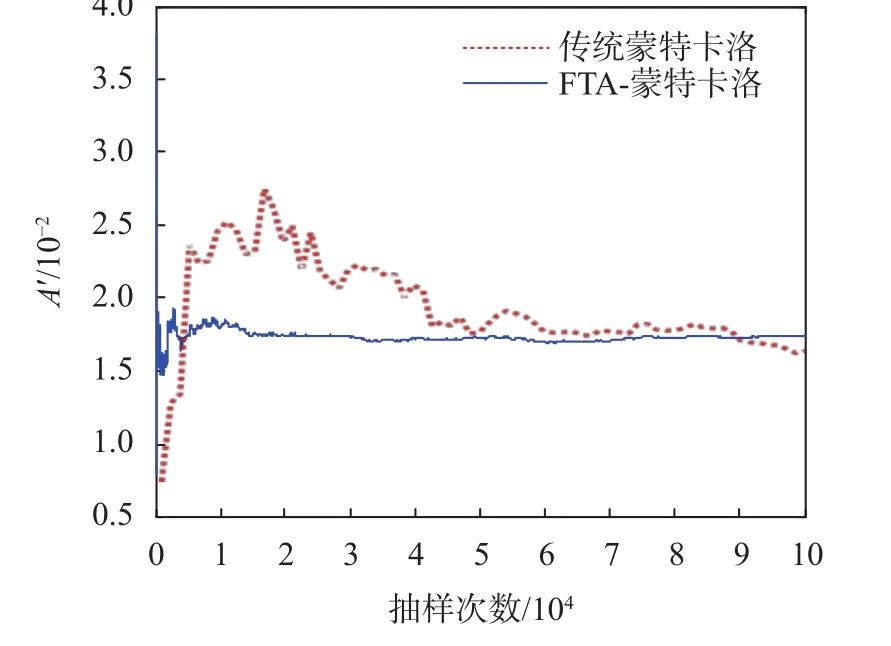
图7 两种方法下的稳态不可用度收敛图

通过MATLAB模拟系统运行，同时也统计出光纤陀螺冗余系统的可靠性指标结果如表3所示，包括：系统平均故障修复时间MTTR、系统平均无故障时间MTBF、稳态不可用度A′以及可用度A的近似值。

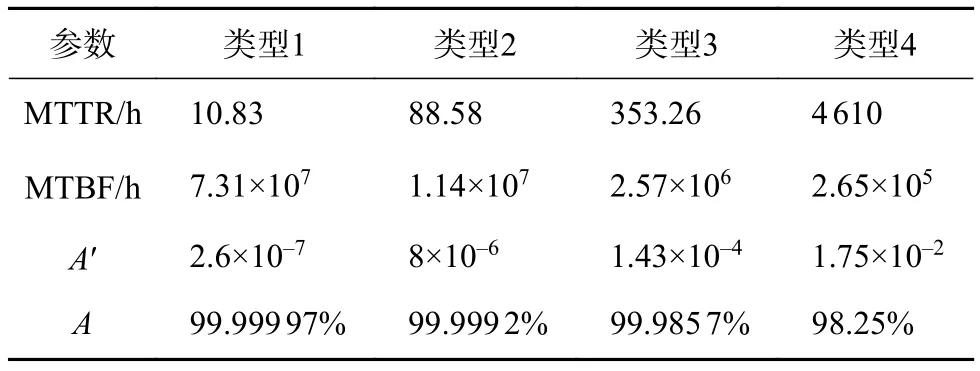
表3 光纤陀螺可靠性指标统计表

由表3可定量看出，维修类型1（元部件参数调整）情况下的可用度最高，为99.999 97%，该情况下的系统平均修复时间约为10.83 h，系统平均无故障工作时间约为7.31×107h。维修类型2（元部件损伤修复）情况下的可用度次之,为99.999 2%，该情况下的系统平均修复时间约为88.58 h，系统平均无故障工作时间约为1.14×107h。维修类型3（元部件失效小更换）情况下的可用度为99.985 7%，该情况下的系统平均修复时间约为353.26 h，系统平均无故障工作时间约为2.57×106h。维修类型4（元部件失效大更换）情况下的可用度最低，为98.25%，该情况下的系统平均修复时间约为4 610 h，系统平均无故障工作时间约为2.65×105h。

由上述指标计算结果可得，当组成冗余系统的光纤陀螺可修复能力越强即修复率越高时，整个冗余系统在任务周期内的稳态可用度越高，从而使飞行试验参数测试系统越可靠。与此同时，由指标计算结果可得：对于本论文的光纤陀螺冗余系统而言，当单个陀螺故障率和维修率服从指数分布，并且在故障率一定的情况下，系统平均修复时间和平均无故障工作时间与单个陀螺的维修率成正比，即当单个陀螺维修率提高为N倍时，系统MTTR和MTBF也相应变为原来的N倍。

5 结束语

本文针对光纤陀螺冗余系统的工作原理及特性，基于故障树原理建立了光纤陀螺可靠性评估模型并采用蒙特卡洛仿真法进行系统可靠性指标求解，定量评估了光纤陀螺冗余系统的可靠性，定量评估了同类光纤陀螺不同修复率对冗余系统可靠性的影响。

本文研究结果表明，当光纤陀螺故障率一定时，其可修复能力对冗余系统平均无故障工作时间、系统平均修复时间以及系统稳态可用度的调节起决定性作用，陀螺修复时间越短，修复率越高，冗余系统稳态可用度越高，可靠性提升幅度就越大。通过定量研究光纤陀螺修复率与系统可靠性指标之间的关系、对比不同维修率下的系统可靠性指标变化，可在冗余系统的初期设计规划阶段，为光纤陀螺冗余系统关键元件的选取、检修及更换制定合理方案，为系统可靠性与经济性协调等方面提供决策依据。