基于线性分位数回归的上证综指量价关系的分析

陆雪妮 朱能辉

（厦门理工学院数学与统计学院,福建 厦门 361024）

0 引言

2014年A股摆脱了连续几年的低迷格局，走出了熊市的阴影；2015年上半年以32%的涨幅赢得了全球的瞩目，牛市成为中国股市的新气象。不过2015年下半年受场外融资链条松动的影响，股市新气象的泡沫迅速破裂，转眼间牛市梦想破灭，股灾令人恐慌至极。这次股灾的杀伤力之大、波及范围之广，在中国资本市场上是史无前例的。经历了这段特殊时期后，中国证券市场正逐步走向成熟，量价关系特点也发生了改变。总结这次股灾的经验和教训，重新定位投资理念，以及对中国资本市场适当的改进改善，则显得非常重要。

上海证券综合指数（上证综指）反映了整个股市行情，对证券指数的预测分析以及趋势研判，可以为投资者的投资决策提供一定的参考。股票市场是多变且复杂的，影响指数波动的因素很多，长期准确预测其走势十分不易,然而，伴随计算机与统计技术发展的进步，对于短期的股指预测将成为可能。Gallant等[1](1992) 指出,与仅对股价的单一变动研究相比较,对股价与交易量的联合动态研究,能够提供更多关于资本市场的信息,特别是根据股指当天交易量对其收盘收益率进行预测。因为不论市场是处于牛市还是熊市的环境下，股票当期的交易量对收盘收益率的影响程度均远远超过历史期收盘收益率的影响，这可能是由于股票当期的交易量与收盘价是同期的原因。而金融时间序列的复杂性模型常常仅适用于特定的假设下。

在商品交易中，销量和价格的相关性非常显著。那么对股票而言，其“量价关系”又是怎样呢？以价格包含交易量的所有信息为隐含的假设前提，传统的资本市场一般均衡理论通常只集中在对价格的分析来研究资本市场。但在实际资本市场运行中,传统假设交易者和市场信息获取，以及对信息反馈的无差异性的前提是不存在的。交易者对信息获取的渠道与方式、反应速度和能力等都存在显著差异,并外化表现为在交易行为上的复杂性，这使得影响资产价格的重要因素必须要包含交易量。

Osborne[2]最早把资本市场交易量纳入资产价格行为进行研究，揭示了股票市场量价之间存在正相关性。Granger 和 Morgenstern[3]实证研究了股票市场的量价关系，得出纽约证券交易市场不存在显著的量价关系，但其后的许多研究则得出不同的结论。借助于卡方检验、方差分析和交叉谱分析等统计方法，Ying[4]得到了包括较小（较大）的交易量往往伴随着股价下跌（上升）等许多量价关系的重要结论。有关量价关系的综述性文献评论由Karpoff[5]完成,大多数的研究结果都认为量价关系存在显著性。

相较而言,国内研究量价关系的相关结论大多支持中国股市存在显著量价关系的说法。基于2005年下半年的中国资本市场数据，李雪[6]在研究股票价格与交易量之间的相关关系时,实证分析发现，在牛市和熊市两种不同的市场行情下，量价关系具备完全不同的特征且有不对称性。魏宝靖[7]先后采用一系列现代计量分析技术，诸如向量误差修正模型、非参数GARCH模型过滤方法等，从线性与非线性的维度探讨分析了牛市和熊市下的量价关系。

上述研究通常只考察变量间的“平均”相关关系,但对不同价格水平下的交易量,往往在资本市场中难以精确地度量，进而无法刻画量价关系的复杂性与多样性。由于正负收益率与交易量之间的相关关系存在的可能差异性,一般文献则是把收益率分为牛市、熊市两个样本进行考察。然而，这种将总体样本分割成条块进行估计的方法,显然无法完整地展现不同收益率与交易量的真实关系,可能会导致严重的偏误。若能从整体上直接去研究日收盘价与日交易量之间的相关关系，那么在一定程度上，更能简洁地提高对指数预测的精度及可靠性。分位数回归更好地反映出变量的分布，以往的研究中极少有人考虑交易量如何直接影响收益率的分位数情况。因此，为弥补上述方法的缺陷和限制,本文将运用线性分位回归分析方法解决这一问题。

1 分位数回归

经典线性回归模型：

模型参数β用来定量描述解释变量X的变化如何影响被解释变量Y的条件均值。传统的普通最小二乘估计(OLSE)在误差服从独立正态分布等假设下是最佳无偏估计量。但上述假设不满足时，诸如误差不服从正态分布、被解释变量出现异常值 (outlier)或数据存在严重异方差性等，OLSE便不再具备上述优良性质且估计的稳健性非常差。另外OLSE仅能提供这些差异的“平均”水平，不能对其分布的其他方面产生影响。与OLSE不同，分位数回归[8](quantule regression,QR)依据被解释变量的条件分位数对自变量进行回归，可估计出被解释变量在不同分位点下模型参数的不同估计，从而揭示出被解释变量的整个条件分布，能更详细地描述变量的统计分布，且QR不对误差项的分布做具体假设，其估计比OLSE更稳健，对异常值也不太敏感。

计算求出样本的第分位数。该方法可以推广到估计条件分位数函数模型。

通过求解下式得出样本的第τ分位数，记作：

现最为广泛应用的QR算法有两种：（1）单纯形法（simple method）:选择一个顶点，然后搜索可行解所围成多边形的边界，适用于样本量不超过5 000，解释变量个数不超过20个的情形；（2）内点算法（interior method）：在可行解所围成的多边形中，并在不超过边界的情况下，随机搜索一个内点，直到搜索到最优点，适用于样本量较大的情况。

1982-1986年，Koenker和Bassett相继研究了线性假设检验[9]、异方差稳健性检验[10]、QR的性质[11]。QR模型的渐进协方差矩阵估计方法（Buchinsky[12]）被进一步探讨并被应用于美国女性薪酬结构变化的研究分析中。QR在计算机的辅助下广泛运用于各个学科领域，尤其在经济学中，QR不仅应用于预测风险价值[13]，而且常用于分析金融时间序列[14]和房地产[15]。

2 上证综合指数的分位数回归分析

2.1 数据及来源和变量设置

以收益率和交易量为变量来刻画上证综指的量价关系。样本选自2014年1月1日到2015年12月31日上证综合指数的日收盘指数P和股市的日交易量q（成股）,对数据中的缺失值进行均值插补,一共获得487个样本。使用R软件的quantmod包，调用getSymbols()函数下载数据，其数据源包括雅虎、谷歌、圣路易斯联邦储备银行的联邦储备经济数据库（FRED）等。

令收益率、交易量分别为

2.2 数据描述性统计特征和单位根检验

从表 1 中收益率的描述性统计特征及图1的时间序列图发现，收益率的偏度和尖峰程度、异方差性都不显著。单位根检验进一步表明，在1 %显著性水平下收益率序列是平稳的；观察图1的交易量时间序列图，虽然交易量略有时间趋势且展现出一定程度的左偏和尖峰状态，但单位根检验表明，在10% 显著性水平下交易量仍是平稳时间序列。

图1 上证指数2014年1月1日到2015年12到31日收益率与交易量的时间序列图

表1 收益率与交易量的描述性统计特征与单位根检验

2.3 分位数回归分析

建立如下量价关系模型：

因为单纯形算法计算稳定且适用于样本量不超过5000，解释变量个数不超过20的情形，所以使用单纯形算法的R命令rq进行QR参数估计。为详细刻画，取0.10、0.20、0.30、0.40、0.50、0.60、0.70、0.80和0.90的分位数回归线。表2对量价关系分别进行OLSE和分位回归估计，并利用秩检验计算QR参数估计的置信区间。在R软件中使用rq命令进行参数估计后，使用summary命令或summary.rq命令可得到参数估计的秩检验置信区间。

观察表2发现，估计结果在不同水平的收益率下有所差异。在5 %显著性水平下，交易量的参数估计值均不为0，且估计值的正负和大小也有显著差异。具体地说，

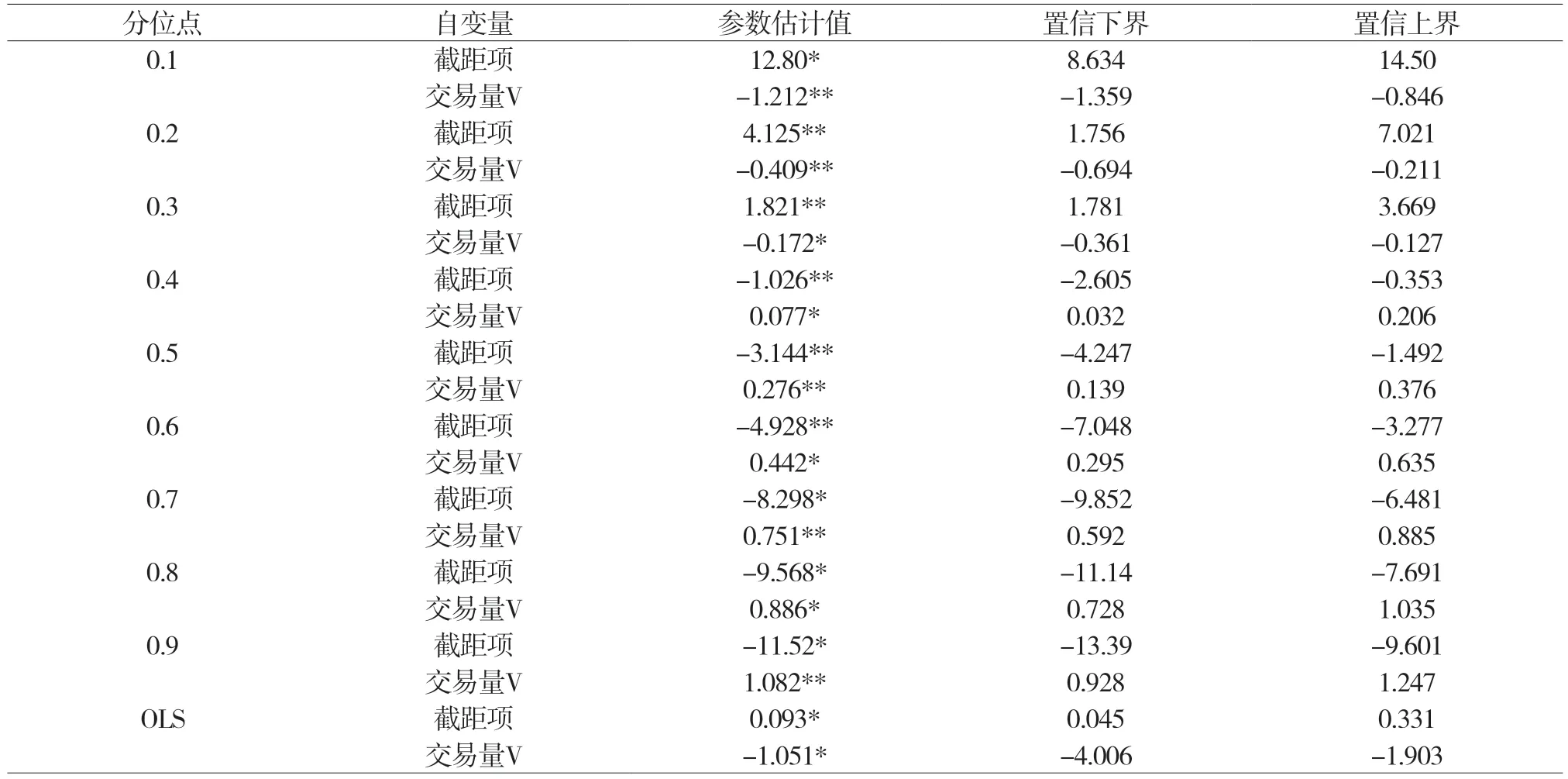
表2 收益率R与交易量V的分位回归结果

估计值从0.1分位点下的-1.212 逐步增加到0.9分位点下的1.082；另外，估计值的绝对值呈先降后升的趋势，并以估计值由负转正的0.4分位点（0.077）为拐点。量价关系在收益率波动的两侧越强烈，且在收益率的低分位点上弱于在其高分位点上。量价关系在收益率向中间分位点接近时逐渐弱化。实证分析的上证综指量价关系与Ying[4]得出的收益率上涨（下跌）通常与较高（较低）的交易量相对应的结论大致吻合，呈现出总体V型非对称的关系（图 3）。

图3 上证指数2014年1月1日到2015年12到31日交易量（日对数交易量）与日收益率的分位数回归拟合图

对表2中的QR与OLSE的结果进行对比发现，交易量的OLS估计量为-1.051，仅大于分位点0.1对应的分位回归估计量，小于80 %以上的分位回归估计量，距离最右端0.9分位点的估计量1.082甚远，仅与分位点0.1的分位回归结果-1.212大致相近。

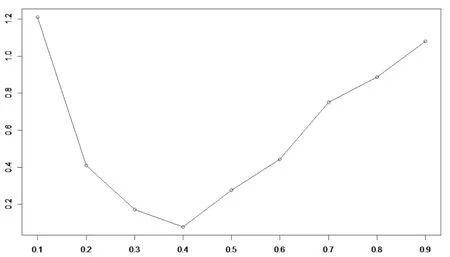
图2 表2交易量V参数估计的绝对值趋势

在图3中，线性均值回归的估计结果用实线表示，分位数为0.5的线性中位数回归估计用长虚线表示，短虚线从下到上分别表示分位数为0.10、0.20、0.30、0.40、0.60、0.70、0.80和0.90时的线性QR估计结果。

拟合值与真实值的平均分位数误差定义为：

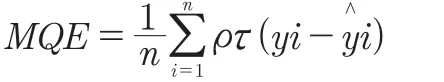
用上证指数2014年1月1日到2015年12到31日交易量（日对数交易量）进行拟合，求出拟合值与真实值之间的平均分位数误差，并进行对比：

表3 各个分位点对应的平均分位数误差

基于拟合值与真实值的最小平均分位数误差，选择分位点为0.4的QR模型作为相对最佳方程，得到线性QR方程：

以2016年1月4日到2016年1月22日的日交易量数据作为预测集，利用回归方程计算出收益率的预测值，再将收益率预测值还原为对应的日收盘价预测值，最后与真实的日收盘价进行对比，计算两者的相对误差，如表4。使用predict.rq的R命令进行QR预测。对比表4日收盘价预测值与日收盘价表明，相对误差在0.193%—7.397%变动，相对误差都比较小，说明该回归方程的短期预测效果良好。

表4 分位点为0.4下预测值与真实值对比

3 研究结论与建议

基于2014年1月1日到2015年12月31日两年的中国资本市场特殊时期的上证指数数据，对日收益率与日对数交易量的相关关系建立线性QR模型。实证分析表明，由传统的普通OLSE所定量描述的量价关系中，股票市场的“平均水平”的量价关系往往过于低估真实的量价关系，致使市场信号难以传递真实的市场信息。

与传统的“平均水平”的量价关系不同，QR模型则更完整详细地反映出不同收益率水平下的各个不同的量价关系，并揭示了股票交易市场的“跟风”效应，即在股市越接近跌停时，投资者大量抛售股票，从而催促股市价格加速下跌；相对应地，在股市越接近涨停时,投资者出手争抢股票，交易量急剧膨胀，进而推动股市价格加速上涨。

最后，基于最小均方误差准则，选取分位点为0.4所对应的回归模型作为预测方程，对应于40%分位点的日收益率可由日对数交易量的变化（线性）来解释。以2016年1月4日到2016年1月22日上证综合指数的日交易量数据作为预测集，利用回归方程计算日收盘价的预测值，并与真实日收盘价进行比对，两者相对误差都较小，说明线性QR模型的短期预测效果良好。

本研究结论可总结为:（1）区别于最小二乘估计方法对收益率条件均值的考察,分位回归方法是以加权平均绝对误差作为目标函数对回归系数进行估计,从而可以对不同分位的收益率进行考察,更完整详细地反映出不同收益率水平下的各个不同的量价关系；（2）交易量与收益率存在显著非对称的V型量价关系,即当收益率为负时,量价关系为负；当收益率为正时,量价关系为正;正向量价关系强于负向量价关系。这种量价关系反映了股市投资群体的“跟风”效应；（3）市场的“平均”量价关系往往低估真实的量价关系，市场信号难以传递真实的市场信息。

随着经济社会的发展，今后可能还将面临比2014—2015年更复杂的局面。因此，本文利用QR模型实证分析这一时期的量价关系，总结这次股灾的经验教训，对资本市场适当的改进改善，尝试提出以下几点建议：

一是尝试探索设立平准基金或准平准基金。针对QR模型实证分析量价关系得出的股票交易市场的“跟风”效应，减少不必要的代价。在资本市场发展的初级阶段，积极培育和弘扬我国资本市场的价值投资理念，尝试探索设立平准基金或准平准基金。其性质上是一种特殊的金融稳定基金，基金主要起稳定市场的作用，当市场短期失灵，尤其是在股灾时期或有可能引发系统性金融风险以及市场过度疯狂时，平准基金或准平准基金适时出手，有助于消弭初期阶段的金融风险。

二是加快市场规则向国际靠拢，局部试点T+0和无涨幅限制。现阶段的T+1和10%涨跌幅限制以及审核制带有计划经济的色彩，这些弊端在这次股灾中暴露无遗。每天10%的无量跌停引发股指期货等量下跌，进而强化下跌预期，导致第二天又一个10%的无量跌停，恶性循环，资本市场始终找不到终止负效应的途径。因此，必须要有一个使得资本市场的价格形成约束机制的制度，局部市场试点T+0和无涨幅限制应该是一个值得推荐的改善办法。

三是积极鼓励和引导投资者用闲钱投资，不借贷，不指望炒股来解决短期财务需求。股灾的发生主要在于投资群体的盲目“跟风”效应，部分投资者暴富心理太强，投资杠杆过高；反之，若是闲钱投资，更会注重基本面的研究，持有具备投资价值的公司股票，就不会被短期波动所干扰，也就不容易借钱去追涨。