非磁性发光材料的磁场效应:从有机半导体到卤化物钙钛矿*

陶聪 王敬民 牛美玲 朱琳 彭其明 王建浦

(江苏省柔性电子重点实验室,江苏先进生物与化学制造协同创新中心,南京工业大学先进材料研究院,南京 211816)

1 引言

磁场效应(magnetic field effects,MFEs)被定义为外磁场引起的材料或器件的光电物理性质变化[1,2],例如改变光致发光(photoluminescence,PL)、电致发光(electroluminescence,EL)、光电流(photocurrent,PC)、注入电流等的强度,导致产生磁光致发光(MPL)[3]、磁电致发光(MEL)[4]、磁光电流(MPC)[5]、磁电导(MC)[4,6]等,其幅值为

其中IB和I0分别表示有磁场和无磁场下的光电信号强度.

不同于传统自旋电子学利用磁性材料实现自旋注入与调控[7,8],本文所说的磁场效应其研究对象本身不含有磁性,而仅仅依靠外加磁场对其自旋态进行调控,因此关于磁场效应的研究极大地丰富了磁电子学的范畴.早在二十世纪六七十年代,研究者就发现一些有机材料溶液或晶体的发光存在磁场效应[9,10].2003 年,波兰物理学家Kalinowski等[11]首次在有机发光二极管(organic light-emitting diode,OLED)中探测到了磁场效应,一个中等强度的磁场(＜0.5 T)就能显著改变不含有任何磁性材料的OLED 器件的电致发光强度和电流(图1(a)和图1(b)).接下来几年,更多的研究表明几乎所有有机半导体的光电特性都对外加磁场存在明显的响应[11-21],表明磁场效应普遍存在于有机半导体中.

图1 基于Alq3 的OLED (a)电致发光和(b)电流的磁场效应[11]Fig.1.Magnetic field effects on (a) electroluminescence and (b) current of Alq3-based OLED[11].

金属卤化物钙钛矿(metal halide perovskite)凭借优异的光电性能、低廉丰富的原材料和简单的制备工艺,正成为发光领域的明星材料[22].仅仅数年,钙钛矿发光二极管(perovskite light-emitting diode,PeLED)的外量子效率(external quantum efficiency,EQE)就从不足1%提升到超过20%,展现了其在照明与显示领域的巨大应用潜力[23-31].最近几年的研究发现,在钙钛矿材料和器件中也存在磁场效应[32-37],这大大拓展了磁场效应的研究范畴,同时也为磁场效应的研究提升钙钛矿光电器件的性能提供思路.

值得注意的是,虽然有机半导体材料与金属卤化物钙钛矿的发光都会受外磁场影响,但两种材料在电子与空穴间距离、载流子输运方式、重金属含量等方面存在差异,使得两者的电子-空穴交换相互作用、自旋-轨道耦合等内部相互作用产生明显不同.因此,两者的磁场效应大小和线形都存在区别.回顾现有的磁场效应研究可以发现,对于钙钛矿磁场效应的理解大都忽略了其特殊的电子结构,而选择借鉴成熟的有机磁场效应理论去解释现象.

鉴于电子结构区别较大的有机半导体与卤化物钙钛材料都呈现出磁场效应现象,因此有必要综合对比分析这两类材料的磁场效应的共同点与差异.本文聚焦于磁场效应在有机半导体和卤化物钙钛矿中的研究进展,特别是磁场对材料和器件发光过程的影响,即发光的磁场效应.通过总结代表性的理论模型和实验数据,分析磁场下有机半导体和卤化物钙钛矿的发光物理行为,试图厘清现阶段对有机及钙钛矿发光磁场效应的理解.最后,针对磁场效应提出了一些自己的看法,希望能对该领域的发展有所帮助.

2 有机半导体发光的磁场效应

2.1 有机磁场效应的研究进展

在过去的几十年里,有机半导体光电器件得到了广泛的研究.其中OLED 因其柔性可卷曲、可视角度大、对比度高、色域广等优势,取得了巨大的成功,已经广泛应用于智能手机、个人电脑、车载显示等.2003 年Kalinowski 等[11]发现,基于小分子材料Alq3的OLED 在最大300 mT 外加磁场下,其发光和电流分别增大了5%和3%,即MEL和MC 分别为5%和3% (图1(a)和图1(b)).由于该OLED 不含有磁性材料,因此当研究者得知一个较小的磁场就能显著改变器件的光电性质时,磁场效应立刻成为了领域内的一个热点.

从首次发现到不断深入研究,科研人员一直在尝试获得更大的有机磁场效应.在Kalinowski 等[11]首先观察到有机半导体的磁场效应之后,2007 年,Wohlgenannt 课题组[13]研究了 π -共轭有机分子的磁场效应.室温下,对基于Alq3的小分子单层器件仅仅施加100 mT 的磁场,就得到了56%的MEL和27%的MC (图2(a)和图2(b)).2011 年田纳西大学的胡斌课题组[12]基于洛伦兹力效应,得到了大于400%的发光磁场效应(图2(c)).通过改变磁场角度、电压和溶液浓度,他们发现洛伦兹力驱动的离子传输和洛伦兹力依赖的液体对流扩散层厚度关系是巨大磁场效应的原因.2013 年,印度新德里贾瓦哈拉尔·尼赫鲁大学Mahato 等[20]将一维分子材料(N,N′-双(2,6-二甲苯)苝-3,4,9,10-四羧酸二酰亚胺)(DXP)嵌入到沸石晶体中.独特的一维材料结构设计,使得电流输运在外磁场与内磁场之间的竞争下被自旋限制,因此在室温下和仅仅几毫特斯拉的磁场下就得到了大于2000%的MC(图2(d)).2015 年,爱荷华大学Wang 等[21]同样基于在纳米尺度上改变分子的空间结构,在室温和小磁场下,热活化延迟荧光混合物中的激基复合物发光产生了超过60%的MEL.进一步,他们通过调节器件的电流-电压响应曲线,实现了超过1000%的MC 和4000%的MEL (图2(e)和图2(f)).

图2 Alq3 器件在不同电压下的(a) MC 和(b) MEL[13];(c) Ru(bpy)3 器件在不同电压下的MEL[12];(d)不同长度一维结构器件的MR[20];延迟荧光器件在不同温度下的(e) MC 和(f) MEL[21]Fig.2.The (a) MC and (b) MEL of Alq3-based OLED at different voltages[13];(c) the MEL of Ru(bpy)3-based OLED at different voltages[12];(d) the MR in the device with one-dimensional structure[20];the (e) MC and (f) MEL of delayed fluorescence OLED at different temperatures [21] .

2.2 几个常见的物理模型

有机半导体中普遍存在的磁场效应使研究者对理解其背后的物理机制十分着迷.然而,在无机磁场效应的众多物理机制中,没有一个能够合理解释有机半导体的磁场效应[14].例如,用于理解无机自旋阀器件中“巨磁电阻”的机制就无法解释有机磁阻效应[7].因此,基于大量实验数据和OLED 中的激发态类型(图3)[38],研究者们针对有机磁场效应提出了各种理论模型.大体上,有机磁场效应背后的物理机制主要可分为两类:第1 类是磁场改变不同自旋态之间的分布,主要有电子-空穴对(electron-hole pair,EHP)模型[11,39]、三线态-三线态淬灭(triplet-triplet annihilation,TTA)模型[40-42]和热自旋极化(thermal spin polarization,TSP)模型[3,43]等;第2 类是磁场影响载流子的迁移率,包括双极化子(bipolaron)模型[44]和三线态-载流子相互作用(triplet-charge interaction,TCI)模型[45-47]等.下文将简单介绍这两大类理论机制及其相关代表性实验.

图3 OLED 中载流子相互作用决定的激发态类型[38]Fig.3.Excited states in OLED determined by the interactions between carriers [38] .

2.2.1 电子-空穴对(EHP)模型

图4(a)所示为载流子通过不同路径复合或者解离的过程.根据自旋统计规则,OLED 中载流子注入后,会在库仑力作用下相互靠近形成比例为1∶3 的单线态和三线态EHP[48].此时,电子和空穴之间的束缚力较弱,因此它们可以重新解离为自由载流子,也可以在库仑力作用下进一步靠近形成激子.EHP 模型的核心观点是外加磁场对EHP 自旋态的影响大于超精细相互作用,从而调控单线态与三线态EHP 之间的相互转换,产生自旋混合的效果,最终改变不同自旋态激子的数量分布[11,49].

不同自旋态EHP 之间的转换需要同时满足能量守恒和角动量守恒[50],而单线态和三线态的能量和角动量的差异通常会阻止它们之间的转换.在有机半导体材料中,交换相互作用可以使单、三线态产生能量差,破坏它们之间的简并.对于激子,较强的库仑束缚作用使得电子与空穴间的距离很近,导致较大的波函数重叠进而产生强的交换相互作用,使得单、三线态激子之间存在几百毫电子伏特的能量差[51],激子之间很难发生自旋混合.而在EHP 中电子和空穴之间的距离较大,因此其交换相互作用比较弱,单、三线态EHP 的能级接近[52].在超精细相互作用或自旋-轨道耦合等作用下,单线态EHP 和3 个三线态EHP 都可以发生自旋混合,也就是它们之间可以相互转换,最终达到动态平衡[11,49].若对器件施加外部磁场从而引起三线态EHP 塞曼分裂,那么3 个三线态之间就会失去简并.这种情况下,单线态EHP 只与1 个三线态发生自旋混合,也就是说自旋混合效果减弱了[53,54].由于不同自旋态的EHP 形成激子或者解离成自由载流子的速率不同,外加磁场对EHP 自旋混合的影响最终将改变激子的发光强度,产生MEL;同时也能改变激发态解离成自由载流子产生二次电荷的数量,产生MC[52].

除此之外,二十世纪六七十年代在有机溶液发光磁场效应研究中建立起来的“Δg”模型,在某种程度上也属于EHP 模型[55-58].在该模型中,组成EHP 的两个极化子(即电子和空穴)通常以不同的频率围绕磁场进动(图4(b)),当两者的g因子差值较大时,随着磁场的增大,电子和空穴的自旋进动频率差 ΔωP=µBΔgB/ℏ (其中µB为玻尔磁子,Δg为电子、空穴g因子差值,B为外部磁场强度,ℏ 为约化普朗克常数)会增大,致使单、三线态之间产生交叉混合,从而导致磁场效应[59].

图4 (a)自由载流子、电子-空穴对和激子的跃迁能级示意图及相关速率常数,其中S 和T 分别表示单线态和三线态,G 表示EHP 的形成 率, 和 分别代 表单线 态和三线态EHP 的离解 速率常 数, 和 为单线 态和三线态EHP 的复合 速率常 数;(b)电子、空穴在磁场下以不同频率 ω 进动示意图Fig.4.(a) Transition rate constants of free carriers,electron-hole pairs and excitons.S and T represent singlet and triplet states,respectively.G represents the formation rate of EHP. and represent the dissociation rate constants of singlet and triplet EHPs,respectively, and are the recombination rate constants of singlet and triplet EHPs.(b) The Larmor precession of electrons and holes with different frequency ω under a magnetic field.

2.2.2 三线态-三线态淬灭(TTA)模型

早在1963 年,Sternlicht 等[9]就在有机晶体中观察到延迟荧光现象,并提出了三线态-三线态淬灭模型.近年来的研究表明,许多荧光OLED 的高效率都得益于TTA 产生的额外单线态激子[60-64].1967 年,Johnson 等[41]发现有机材料中由TTA产生的延迟荧光在外磁场下会发生明显的变化.1968 年,Merrifield[65]基于量子力学建立了激子动力学模型,为TTA 的磁场效应给出了理论解释.

区别于EHP 模型中单、三线态的自旋混合,TTA 过程中单线态只是产物,磁场影响的是三线态与三线态之间的相互作用[65].TTA 模型基本理念[42,66]如图5 所示.当两个不相干三线态激子的距离缩短到一定程度时,它们会先形成一种三线态-三线态激子对(T-T pair)的中间态.随后,根据激子对的自旋波函数属性,它会演化成一个基态外加一个单线态或者三线态或者五线态的组合[42].由于TTA 过程需要两个三线态参与,因此其作用强度与三线态激子浓度的平方成正比.在TTA 过程中,三线态-三线态激子对所蕴含的单线态属性会受外加磁场的影响,导致生成的单线态激子概率受外磁场控制,从而产生MEL[62,67].应当注意到,TTA 模型一般不能直接解释磁阻或磁电导现象.

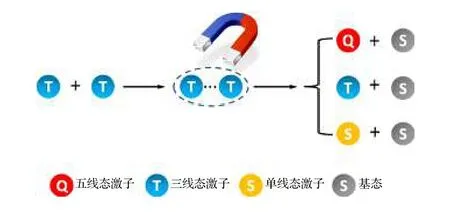
图5 三线态-三线态淬灭(TTA)模型示意图[66]Fig.5.Schematic diagram of the triplet-triplet annihilation(TTA) model [66] .

2.2.3 双极化子(Bipolaron)模型

在有机半导体中,一般可将极化子等同于载流子[48].双极化子模型最早于2007 年由Bobbert等[44]提出.在有机材料中,电流的产生是通过载流子在各个位点之间的跳跃实现的.双极化子模型认为在强的电子-声子耦合条件下,载流子会在能量较低的跳跃点上形成同性电荷的双极化子[68].根据泡利不相容原理,在同一空间出现自旋相同极化子的概率为零.因此,双极化子只能为自旋单线态,这种效应被称为“自旋阻塞”[69].没有外加磁场时,载流子主要受超精细场的作用,其方向是随机的.载流子不同位点上受到不同的超精细场作用,产生不同方向的自旋进动,使载流子可以发生自旋翻转.因此,在载流子跳跃过程中,可以通过自旋翻转克服“自旋阻塞”,形成双极化子,如图6(a)所示.在施加较大外磁场下,超精细场几乎可以忽略不计,载流子的自旋方向会倾向于外磁场方向,导致载流子在跳跃过程中难以改变自旋方向,致使双极化子因为“自旋阻塞”而难以形成.此时,载流子只能寻找其他空位点进行传输[38],如图6(b) 所示.

图6 (a)双极化子的形成过程;(b)外磁场下双极化子形成概率减小;(c)利用双极化子模型拟合磁场效应[44]Fig.6.(a) Formation process of the bipolaron;(b) the probability of the bipolaron formation decreases under the external magnetic field;(c) fitting the magnetic field effect with the bipolaron model [44].

可见,一方面,外加磁场使得自由载流子形成双极化子的概率减小,减少了载流子在跳跃过程中的可占据位点,从而降低了器件的电流,形成负的MC.另一方面,双极化子形成概率减少使得更多电荷以迁移率更高的自由载流子形式存在,增大了平均迁移率,增大了电流,从而产生正MC.因此,器件总的磁场效应取决于这两个过程的竞争,磁场对载流子迁移率的影响进一步又会导致器件EL的变化,产生MEL.Bobbert 等[44]利用蒙特卡罗模拟研究了双极化子模型,根据磁场下双极化子形成或解离与跳跃之间的关系,获得与实验数据一致的线型,如图6(c).

2.2.4 三线态-载流子相互作用(TCI)模型

根据跃迁选择定则,大多数有机材料中三线态到基态的跃迁是自旋禁阻的.因而器件在工作过程中,发光层内会存在大量长寿命的三线态激子.这些三线态激子虽然不能辐射跃迁,却可以将能量转移给载流子回到基态[70],这一过程被称为三线态-载流子相互作用.根据TCI 模型,载流子与三线态激子的相互作用可能通过以下两种路径实现:

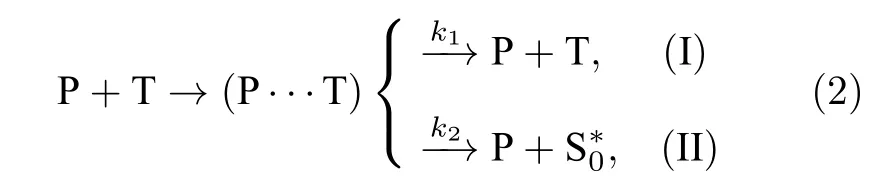
其中P 为自由载流子,T 为三线态激子,(P···T)为TCI 过程的中间态,为基态的振动能级.过程(I)描述的是自由载流子被三线态激子散射,其速率常数为k1.过程(II)描述的是三线态激子与自由载流子作用后,将能量给载流子产生高能载流子,自身回到基态,其速率受k2控制.

2007 年,Desai 等[45]认为自由载流子的迁移率受到三线态激子散射的影响,即三线态激子是载流子传输的阻碍点.通过电子-空穴对模型可知,外加磁场会改变三线态和单线态之间的数量分布,使得三线态浓度降低,导致三线态对载流子的散射作用减弱(图7(a)和图7(b))[38],因此磁场下会得到正MC,同时单线态浓度增大意味着产生正MEL.Desai 等[46]进一步研究发现,TCI 模型也可能带来负的MC.三线态激子与自由载流子作用后,将能量传递给载流子产生高能载流子,从而增大器件的总电流.Hu 等[5,47]认为在TCI 过程中,三线态激子能够将能量传递给处于陷阱态的载流子,使其获得能量从而脱离陷阱(de-trap),产生额外的载流子.磁场减弱TCI 作用就会减小三线态带来的二次电流,产生负的MC,进而引起负的MEL.总的来说,根据TCI 模型,MC 是正负贡献的叠加,而这些都源于磁场引起的单线态与三线态数量分布的变化.

图7 (a)无外加磁场和(b)有外加磁场下三线态激子对自由载流子的散射作用[38]Fig.7.Scattering effects of triplet excitons on free carriers(a) without and (b) with an external magnetic field [38].

2.2.5 热自旋极化(TSP)模型

载流子保持一个特定自旋方向排列的状态叫做自旋极化[71-73].通常,OLED 中自由载流子从电极注入到活性层时其自旋方向是随机的,基于自旋统计,最终形成比例为1∶3 的单线态和三线态激子[74-76].在自旋电子学相关研究中,通过使用铁磁性电极,可以在一定程度上控制注入载流子的自旋方向,在活性层中形成特定自旋方向的载流子,这被称为自旋极化注入[77-79].但目前为止,有机材料的自旋极化注入效率仍然较低.2012 年,王建浦等[3]首先发现在低温和高磁场环境下,当载流子自旋沿z轴取向的塞曼能量与环境热能kBT(kB为玻尔兹曼常数,T为温度)相当时,有机半导体材料中电子和空穴的自旋方向将倾向于与外磁场对齐(图8(a)),产生载流子的自旋极化,这一模型被称为TSP 模型.

Scharff 等[43]随后进一步验证了此模型.他们研究的OLED 能够在低温下同时发出荧光和磷光,测试发现在低温高磁场下载流子能够完全自旋极化,此时器件中的电子和空穴只能形成三线态激子,器件的荧光发射被强烈抑制,甚至几乎完全消失,而磷光发射可增强34%(图8(b)).值得注意的是,自旋极化对于环境热和电流密度十分敏感,只有低温和低电流下MEL 才会明显,升温和电流密度增大都会抑制TSP.为了产生TSP,载流子必须在器件中驻留足够长的时间,以便能通过自旋晶格弛豫在电场中平衡.器件电流越高,载流子停留时间越短,两个载流子自旋之间散射的概率越大,使得自旋方向再次随机化.太高的环境热也会造成同样的影响.

图8 (a)有机光电器件中的自旋极化效应,其中绿线为外磁场方向[3];(b)自旋极化下荧光发射被强烈抑制而磷光发射增强[43]Fig.8.(a) Spin polarization in OLED,where the green line is the direction of the external magnetic field[3] ;(b) the fluorescence is strongly suppressed while the phosphorescence is enhanced by TSP[43] .

2.2.6 不完美的物理模型

需要指出的是,以上模型中,只有TSP 模型是建立在严格的统计物理学基础之上的,而其他模型都或多或少含有猜想的性质.此外,许多实验表明,有机磁场效应不仅与材料和器件结构相关,还与测试条件及样品工作环境有很大的联系.在一些情况下,仅仅是稍微改变温度或者偏压等参数,就会使磁场效应产生明显的变化[14-19].以上总结的几个主要的物理模型,都不能单独解释所有的实验现象.以往的研究中,为了解释某个磁场效应实验现象,经常需要根据器件的实际状态而对现有模型进行修正[80].此外,结合多个物理模型共同解释某个现象的例子也不胜枚举[81].在经历了近20 年的研究后,目前有机磁场效应依然没有达成完全意义上的共识,而仅仅在某些小的层面上获得了大多数研究者的认可,例如磁场影响隙间窜越和TTA 过程从而产生的指纹性MEL 曲线等.令人欣慰的是,即便是这些小的共识,也已经让磁场效应成为研究有机光电器件物理机制的一种有力手段.目前,利用磁场效应作为研究工具,已经探讨了OLED 中的反向隙间窜越[50,82]、能量传递[83]、延迟荧光机制[84],以及有机光伏器件中的单线态裂分(singlet fission)[85]等一系列电子过程,为高性能器件的开发提供了依据[86].此外,高能态反向隙间窜越过程对磁场的响应正得到越来越多的关注,而利用磁场效应研究高能态电子自旋相关过程也逐渐成为一个热点[82].

3 金属卤化物钙钛矿发光的磁场效应

3.1 钙钛矿材料结构与自旋相关电子结构

金属卤化物钙钛矿是一类性能优异的新型半导体光电材料,其三维晶体结构分子式可以表示为ABX3[87].通常,A位为甲胺(CH3NH3+)等有机阳离子,B位为铅(Pb2+)、锡(Sn2+)等二价金属阳离子,X位为氯(Cl—)、溴(Br—)、碘(I—)等卤素阴离子.其中每个B位阳离子与周围6 个X位阴离子通过配位作用形成[BX6]4—八面体.钙钛矿晶体可以看作[BX6]4—八面体通过共顶点X位长程有序排列,而A位阳离子占据立方八面体的间隙,维持系统电中性(图9)[87].作为一种可低温溶液旋涂制备的半导体材料,钙钛矿薄膜的载流子扩散距离大[88],迁移率高[89],且在可见光波段范围内拥有优秀的吸收特性[90].因此,近些年钙钛矿光伏器件领域发展迅速,最高光电转换效率已经超过传统的多晶硅等薄膜太阳能电池,达到25.5%[91].同时,高载流子迁移率和高荧光量子效率使得钙钛矿材料也适用于发光器件,基于卤化物钙钛矿材料制备的高效LED 成为了研究的热点[23-31].

图9 金属卤化物钙钛矿的晶胞结构[87]Fig.9.Crystal structure of the metal halide perovskites[87].

由于铅、锡、碘等重元素的存在,金属卤化物钙钛矿中的自旋-轨道耦合作用(正比于原子序数的4 次方)十分强烈[92,93].此外,研究者发现三维钙钛矿在室温下并非是完全对称的四方(或者立方与正交)晶系,晶格中的铅碘八面体BX6会产生扭曲,并且A位有机阳离子也会呈一定取向性转动,造成中心反演对称被破坏[22].基于这些特点,2013年,Even 等[36]利用密度泛函理论和K·P微扰发现三维MAPb(Sn)I3体系的导带与价带都会产生偏离k空间对称中心的分裂,并且这个分裂依赖于能带上载流子的自旋方向(图10(a)).2014 年,Kim等[94]在研究钙钛矿的Rashba 效应时,基于紧束缚模型分析和第一性原理计算,得到钙钛矿导带底为自旋-轨道耦合态,轨道角动量L=1,自旋角度量S=1/2,总角动量存在J=3/2 或1/2,其中J=1/2 为低能级子带.而价带顶因为轨道角动量L=0,表现为完全的自旋态,总角动量为J=S=1/2 (图10(b)).

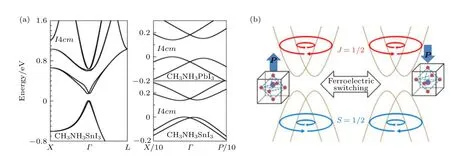
图10 (a)钙钛矿中不同自旋态的子能带偏离k 空间的Γ 点[36];(b)导带与价带表现出自旋极化方向相反的分裂[94]Fig.10.(a) Sub-bands with different spins states deviate from the Γ point in the k space of perovskites[36];(b) the conduction band and valence band show opposite spin splitting depending on the spin polarization direction[94] .

3.2 钙钛矿磁场效应研究进展

从磁场效应角度考虑,钙钛矿与有机半导体存在两点显著的区别:首先,有机半导体材料一般不含重原子(磷光材料除外),自旋-轨道耦合很弱.而钙钛矿材料含有铅等重原子,表现出非常强的自旋-轨道耦合效应[22].其次,由于有机材料中电子和空穴的局域性,电子-空穴交换作用非常强(热活化延迟荧光材料除外),而三维钙钛矿材料的电子和空穴是离域的,导致电子-空穴交换作用很弱.磁场效应之所以能够产生,一个重要原因是外磁场与内磁场(即超精细相互作用或自旋轨道耦合)之间的竞争,这就要求内磁场不能太强,而有机半导体正是如此.因此,根据以往的有机磁场效应理论,较小的外加磁场不太可能在钙钛矿中引起可观测到的磁场效应.然而,国内外几个课题组的研究结果却表明,在普通大小的磁场(＜0.5 T)下能够探测到钙钛矿的磁场效应.

2015 年,美国犹他大学Vardeny 课题组[35]在室温和200 mT 磁场条件下对(CH3NH3PbI3—xClx)的薄膜和发光器件进行测试,分别得到最大为0.28%和—0.25%的MPL 和MEL (图11(b)和图11(c)).他们认为钙钛矿中的重原子(铅、碘)会显著缩短自旋与晶格的驰豫时间τSL,而磁场诱导下弱相互作用引起的自旋态之间的混合时间又大于τSL(图11(a)上),因此钙钛矿很难发生磁场效应.然而,如果钙钛矿 Δg(电子和空穴朗德g因子的差值)的值比较大,不同自旋态之间的自旋进动频率差在磁场下会增大,使得单、三线态之间被诱导产生交叉混合(图11(a)下).也就是说外加磁场依然可以对钙钛矿不同自旋态的电子-空穴对进行调控,进而控制载流子的解离、复合的速率,产生MEL和MPL.为了证实这个模型,他们测量了左右圆偏振光大小对磁场的依赖(图11(d)),并计算了圆偏振度(图11(e)),最终得到 Δg～0.65,算得单三线态之间的转换时间约为80 ps,低于τSL(～200 ps),从而解释了其观察到的磁场效应.

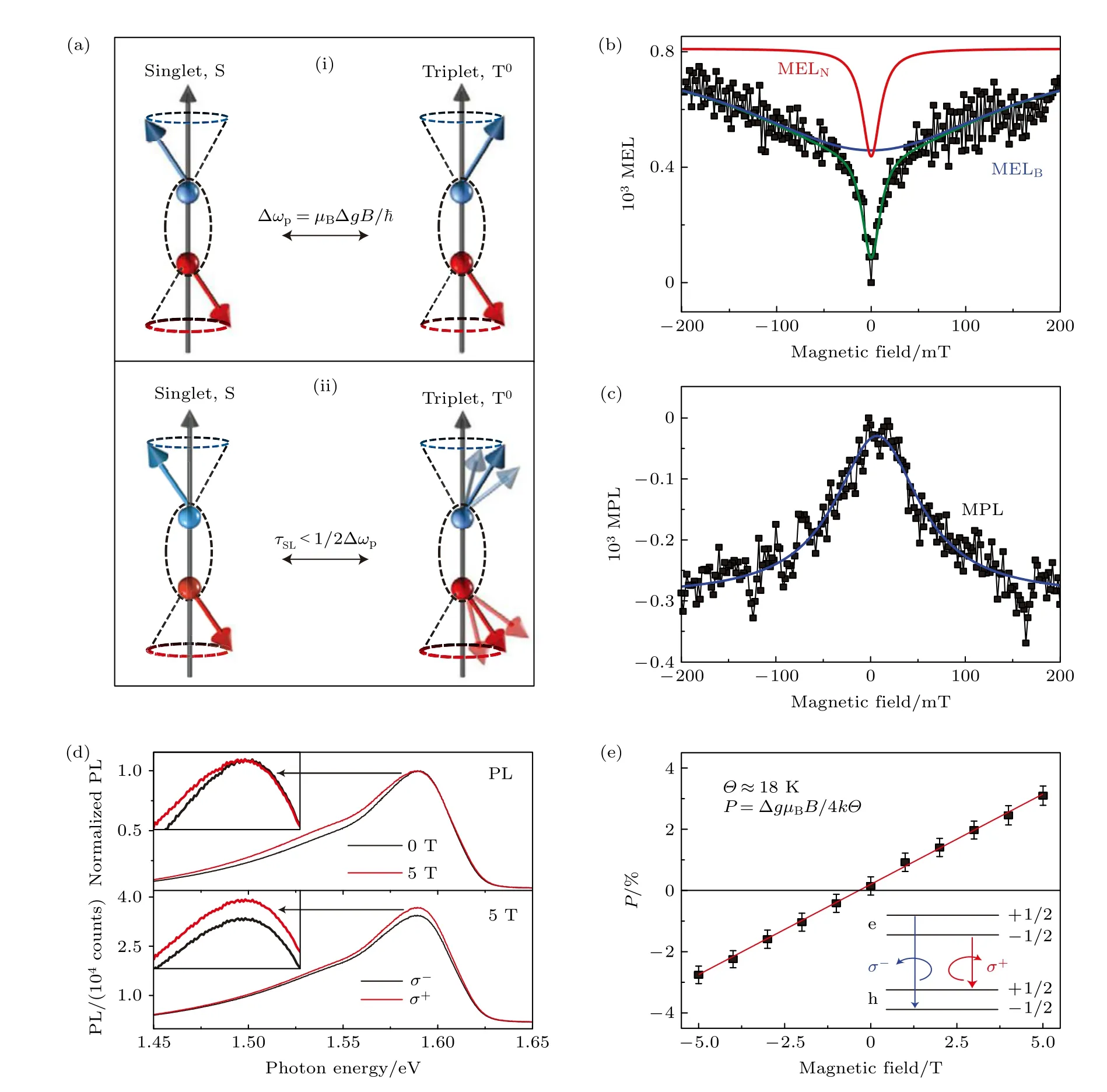
图11 (a)电子-空穴对中Δg 机制示意图;(b) 5 mA 恒定电流下的MEL;(c)钙钛矿薄膜的MPL;(d) 0 和5 T 磁场下左右圆偏振旋光光谱;(e) 18 K 温度下薄膜的圆偏振度与磁场的关系[35]Fig.11.(a) Schematic diagram of the Δg mechanism of electron-hole pairs;(b) the MEL at a constant current of 5 mA;(c) the MPL of the perovskite film;(d) the left and right circularly polarized optical rotation spectra at 0 and 5 T;(e) the relationship between the degree of circularly polarization and the magnetic field at 18 K [35] .

美国田纳西大学的胡斌课题组[33]认为EHP模型适用于钙钛矿磁场效应,他们在室温和低磁场下使用不同光强激发钙钛矿薄膜和器件,发现MPL 和MPC 对激发强度有明显的依赖关系(图12(a)和图12(b)),且MPL 和MPC 的幅值符号相反(图12(c)).他们认为通过抑制自旋混合来降低电子-空穴对中的反平行自旋态可以减弱单线态激子的形成,导致负MPL.同时,磁场减少单线态激子的形成会导致更多的电子-空穴对解离,从而产生更强的光电流.为了说明磁场效应的EHP机制(图12(d)),他们在另一个工作中对比研究了铅基和锡基钙钛矿光伏器件的MPC,不同的B 位重原子会带来不同强度的自旋-轨道耦合.将锡代替铅时,内部磁场参数从281 mT 下降到41 mT,说明磁场效应可能与自旋-轨道耦合存在联系.

图12 (a)钙钛矿薄膜在不同激发光强下的MPL;(b)钙钛矿光伏器件在不同激发光强下的MC;(c)正MC 和负MPL 的线形特征;(d)钙钛矿中的电子-空穴对模型示意图[33]Fig.12.(a) MPL of the perovskite film with different excitation intensities at room temperature;(b) MC of the perovskite solar cell with different excitation intensities;(c) linear characteristics of positive MC and negative MPL;(d) schematic diagram of the electron-hole pair model in perovskites [33] .

不发光(或发光很弱)的暗态在外加磁场下产生发光(或发光增强)是磁光学中的一种常见现象.通常,它源于两种不同的机制,第1 种是激子波函数的收缩导致振子强度的增大,第2 种是自旋态的混合允许暗态通过磁耦合从亮态“借用”振子强度,即不同态的波函数产生混合[95].日本索菲亚大学的Ema 等[32]认为后者是引起二维钙钛矿磁场效应的机制.他们在10 K 下使用超短脉冲激发(C4H9NH3)2PbBr4,观测到了3 个精细结构能级(图13(a)).其中,Γ1和Γ2为自旋禁阻的暗激子,但是因为晶格畸变破坏了跃迁规则,使得这两个暗激发态可以被观察到,在快速自旋驰豫下(图13(b)),它们的PL强度甚至大于自旋允许的Γ5的发射强度.通过3 个精细结构的能级位置,Ema 等估计出交换能约为31 meV.激子的交换作用强度对其玻尔半径十分敏感,如此大的交换作用能表明激子之间的波函数重叠程度很大.图13(c)为PL 的磁场依赖性,随着磁场的增大,Γ2的PL 明显增强,在5 T 时Γ2的PL 强度是0 磁场时的1.4 倍.分析认为磁场效应的产生与Γ2和Γ5的波函数混合有很大关系.

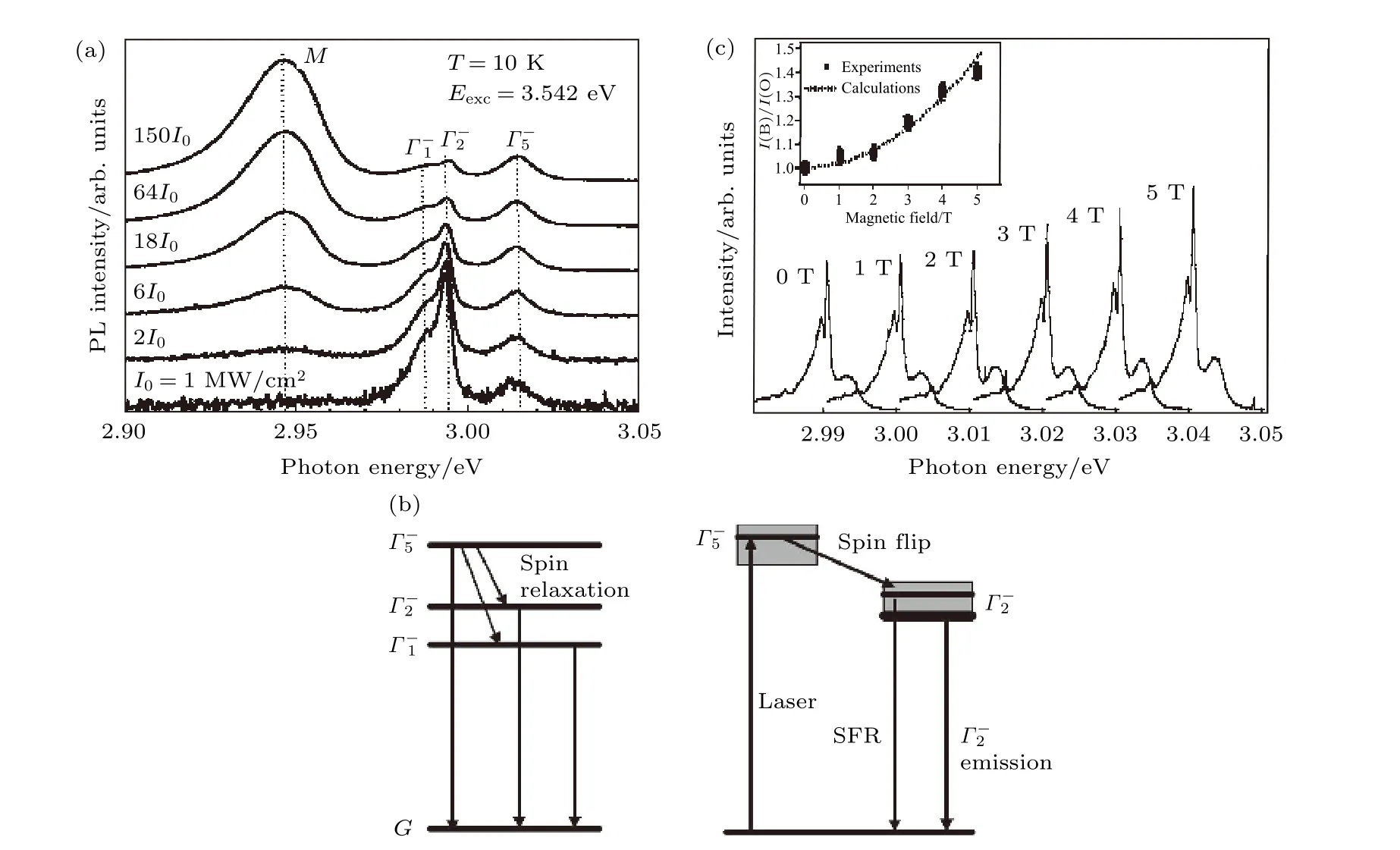
图13 (a) (C4H9NH3)2PbBr4 的PL 谱,其中Γ1 和Γ2 为暗态,Γ5 为亮态;(b)自旋驰豫(左图)和自旋翻转(右图)示意图;(c) PL随磁场的变化[32]Fig.13.(a) PL spectra of (C4H9NH3)2PbBr4,where Γ1 and Γ2 are dark states,and Γ5 is bright state;(b) schematic diagram of the spin relaxation (left) and spin flip (right);(c) the PL changes under the magnetic fields[32] .

有研究表明,磁场不仅能影响不同自旋态激子的数量,也可能会影响辐射跃迁速率,从而产生磁场效应.瑞典乌普萨拉大学的Pavliuk 等[34]制备了全无机CsPbX3(X=Cl,Br,I)纳米晶,研究了磁场对于CsPbBr3纳米晶PL 寿命的影响.他们在0 ℃下施加500 mT 的磁场,发现PL 强度明显减弱,产生了高达15%的下降,同时PL 峰宽变大(如图14(a)).在时间分辨光致发光(TRPL)测试时,他们发现仅仅施加了50 mT 的外加磁场,纳米晶的TRPL 信号就会发生明显的增宽,寿命显著缩短(图14(b)和图14(c)).此外,不管有没有磁场,辐射复合都可用双指数函数实现很好的拟合(图14(d)和图14(e)),说明复合由快(≈ 100 ps)和慢(≈ 1000 ps)衰变两部分组成.他们将双指数辐射衰变解释为非对称复合,快分量归因于强相互作用的电子-空穴对复合,而慢分量为失去相互作用的自由载流子的复合.磁场下,两种复合的寿命都会降低,其中快分量的变化更明显(表1),导致PL 信号的减弱.

图14 (a) 0 ℃下,CsPbBr3 薄膜有/无500 mT 的PL 光谱;(b)无磁场和(c)有磁场的瞬态PL 光谱;(d)无磁场和(e)有磁场下515 nm 处复合动力学轨迹[34]Fig.14.(a) The PL spectra of CsPbBr3 film with/without a magnetic field of 500 mT at 0 ℃;the time resolved PL spectra in the obsence (b) and presence (c) of a magnetic field;the recombination kinetics extracted from the time resolved PLs in the obsence(d) and presence (e) of a magnetic field [34].

表1 光生载流子复合动力学常数[34]Table 1.Recombination kinetic constants of photogenerated carrier [34] .

4 总结与展望

本文回顾了有机半导体和金属卤化物钙钛矿材料及器件发光的磁场效应.在经历了十几年的研究之后,目前有机磁场效应的研究依然存在大量分歧.为了合理解释数据,研究者根据磁场下的不同自旋载流子(激发态)之间相互作用提出了各种物理模型或者假设,包括电子-空穴对模型、三线态-三线态淬灭模型、热自旋极化模型、双极化子模型和三线态-载流子相互作用模型等.但很难有一种模型能作为一般性的机制解释所有的实验现象.也许,正是由于有机半导体材料多种多样的化学组合和结构,造成其电子结构、固态形貌千差万别,因此要想获得一个万能的磁场效应模型将面临着较大的挑战.而研究者们通过分子设计,调整器件结构、控制测试条件等方法来解释特定条件下的磁场效应,或许更有现实意义.

作为新型光电器件,钙钛矿发光二极管表现出十分优异的性能.重要的是,钙钛矿材料的自组装特性使其能够通过低成本的溶液法来实现对材料电学和光学特性的调控.通过调节前驱体组分,能够实现从三维到二维或者多量子阱钙钛矿的制备与调控.对于低维钙钛矿材料,丰富多样的有机势垒层为体系提供不同强度的介电限域与量子限域效应.这些都可以显著改变钙钛矿中激子结合能、有效质量、振子强度、发光寿命等.从这个角度看,磁场效应有潜力成为理解钙钛矿光电物理过程的一个重要手段.通过研究磁场下不同组分,器件结构,工作条件下的钙钛矿材料的光电特性,进而揭示并掌握其优异光电性能的原因.

然而,目前钙钛矿磁场效应的研究还处于起步阶段.由于钙钛矿磁场效应与有机磁场效应的现象较为相似,因此已报道的都是采用有机磁场效应的机理来解释钙钛矿磁场效应,但有机磁场效应的机理是否适用于钙钛矿材料体系还有待进一步的论证.另一方面,目前的钙钛矿光电器件大多都包含有机材料层(例如有机载流子传输层或界面层),这就使钙钛矿磁场效应的研究更加复杂了.很难区分磁场效应是钙钛矿器件中有机层导致的,还是钙钛矿层本征的特性.此外,目前针对钙钛矿磁场效应尚缺乏系统研究,主要表现在以下三方面.1)材料体系单一,目前的研究大多基于三维铅基钙钛矿材料.钙钛矿光电材料正朝着维度调控和组分替换的方向发展.随着钙钛矿材料维度的变化,其光电性质(如激子束缚能、电子-空穴交换作用等)将会受到显著影响;例如替换钙钛矿中的二价金属离子,其自旋-轨道耦合强度将会发生变化.这些性质都与磁场效应息息相关.2)测试条件单一,目前的报道多为室温环境下的磁场效应,缺少对磁场效应温度依赖关系的研究.温度对钙钛矿的性质有极大的影响,例如产生相变、改变带隙宽度等.3)研究手段单一,目前对钙钛矿磁场效应的研究都采用稳态方法,即用恒定电压、连续激光驱动器件.基于瞬态方法(用脉冲电压或激光驱动器件)的磁场效应研究鲜有报道.瞬态方法有其特殊的优势,例如不同时间尺度下的信号对应器件中不同的物理过程(载流子输运、载流子-激子相互作用等).

阐明磁场效应的物理机制不仅具有重要的科学意义,也能为基于磁场效应发展新的应用提供理论指导.例如,自旋电子器件中的极化信号传输是个有着实际应用的问题.传统铁磁性电极的极化信号通常受成膜质量、界面传输等因素影响,自旋注入效率较低.而外加磁场对载流子输运和激发态自旋状态进行控制,在有些条件下甚至产生完全极化的发光信号,这使得功能多样的自旋电子器件开发有了新的可能.对此方面感兴趣的读者可以进一步阅读相关著作[96-98].

显然,磁场效应还有大量的未知等待着研究者的探索.我们期待着磁场效应的进一步发展,为理解有机及钙钛矿光电器件物理贡献应有的力量.同时,我们也期待着钙钛矿光电材料与器件的飞速发展,能够让非磁性发光材料磁场效应这一延续了二十年的课题焕发新的活力.