固态单自旋量子控制研究进展

2022-03-30李廷伟荣星2杜江峰2

物理学报 2022年6期

李廷伟荣星2)† 杜江峰2)

1) (中国科学技术大学,中国科学院微观磁共振重点实验室和物理学院,合肥 230026)

2) (中国科学技术大学,中国科学院量子信息与量子科技创新研究院,合肥 230026)

1 引言

量子力学的诞生,改变了人们以往对于微观世界的认识.量子力学提供了一种全新的视角去研究微观的量子系统.利用经典体系去模拟研究量子系统,是有局限的.更加直接、深入的研究,必须在量子体系上进行.而想要以量子系统为实验平台开展研究,关键在于能对微观量子系统实现精准有效的量子控制.然而由于实际物理体系无时无刻都与环境存在相互作用,相干纠缠等量子特性极易受环境噪声影响.因此量子态的“寿命”是有限的,一般用相干时间来衡量.理想的量子实验平台需要相干时间长且易于操控的系统,固态自旋正是这样的量子体系.固态自旋体系主要包括量子点体系和固态掺杂体系.量子点体系中电子受到三维势阱的约束形成分立的能级结构,这与原子中的电子结构类似,所以量子点又称为“人造原子”.门控量子点[1]是一类广泛应用于量子计算领域的量子点,它是通过在半导体上刻蚀金属门电极,施加电压对电子约束形成的.门控量子点有两种量子比特的编码方式:一种是将单量子点中电子自旋能级编码成自旋量子比特;另一种是利用金属电极构造出双量子点结构,把电子在双量子点中的位置编码成电荷量子比特.通过电脉冲和微波脉冲可以分别实现对电荷量子比特和自旋量子比特的量子控制.目前量子点中实现的单比特和两比特量子逻辑门保真度分别为99.9%[2]和98%[3].磷硅体系是将31P 原子注入到28Si 衬底中形成的固态掺杂体系,31P 原子核和其上方的电子自旋构成两比特系统.通过激光泵浦可以对核自旋和电子自旋进行初始化[4].磷硅体系中通过微波和射频脉冲实现的单比特门保真度能达到99.9%以上,利用电子自旋之间的交换作用能实现两比特门,保真度达到90%[5].金刚石氮-空位(nitrogen-vacancy,NV)色心,是另一种重要的固态掺杂体系.它在室温下有很长的相干时间,具有优秀的能级结构,可以通过激光方便地对量子态进行极化和读出,通过微波和射频脉冲能实现普适的量子控制.这些良好的物理性质使得NV 色心成为量子物理领域的热点.本文介绍NV色心的量子控制技术进展和在实验研究中的应用.

2 金刚石NV 色心自旋体系

2.1 NV 色心的能级结构和光学读出

金刚石中一个碳原子被氮原子取代,同时邻近的一个碳原子缺失所形成的晶体缺陷(如图1 所示),称为氮-空位缺陷色心,即NV 色心[6—9].NV色心具有C3ν对称性,其对称轴沿氮原子和空位的连线方向,称为NV 主轴.NV 色心有两种电荷态:中性的NV0和带负电的NV—.它们的能级结构和物理性质都有很大的不同,广泛应用于量子物理领域的是带负电的NV—.若无特殊说明本文中的NV色心均指NV—.

图1 金刚石中NV 色心结构图[9]Fig.1.Schematic atomic structure of the NV center in diamond[9].

NV 色心的能级结构见图2(a),其中基态3A2是自旋三重态,可等效为S=1 的电子自旋[10,11].激发态3E 也是自旋三重态,且与基态的能级差为1.945 eV,对应的吸收波长为637 nm.除此之外还存在两个自旋单态的亚稳态1A2和1E,它们之间的能级间隔为1.190 eV,对应的吸收波长为1042 nm.图2(b)是NV 色心电子自旋基态的能级结构图.当没有外磁场时,电子自旋的|ms=±1〉能级简并,且与|ms=0〉能级之间存在D=2870 MHz 的零场劈裂;当沿主轴方向存在外磁场时,|ms=±1〉能级发生塞曼分裂而解除简并.塞曼劈裂大小ωe=γeB0与沿主轴方向的磁场B0成正比,γe是电子自旋的旋磁比,大小为2.8 MHz/G (1 G=10—4T).一般以基态的|ms=0〉能级作为量子比特的|0〉态,选择|ms=±1〉能级中的一个作为量子比特的|1〉态,构成NV 色心的电子自旋量子比特.由于与邻近13C 和14N 等核自旋存在耦合,NV 色心电子自旋的基态能级会发生超精细劈裂[12].类似地选取核自旋的两个能级作为量子比特的|0〉态和|1〉态,构成核自旋量子比特.NV 色心电子自旋和一个邻近核自旋就组成了两比特量子系统.

图2 金刚石NV 色心能级结构[9] (a) NV 色心的基态、激发态和亚稳态;(b) NV 色心基态的精细结构和14N 核带来的超精细结构Fig.2.Energy level diagram of the NV center in diamond[9]:(a) Ground state,excited state and metastable state of the NV center;(b) fine structure and hyperfine structure(caused by 14N nuclear spin) of the NV center ground state.

室温下由于声子作用,NV 色心可以被500—600 nm 波长的激光激发,从基态跃迁到激发态.处于激发态的NV 色心有两种路径回到基态:一种是通过自旋守恒的自发辐射回到基态,同时产生波长637—750 nm 的荧光,称为辐射跃迁过程;另一种是通过两个亚稳态能级1A2和1E 回到基态,称为系间跨越(intersystem crossing,ISC)过程[13].ISC过程自旋不守恒,并且由于亚稳态1A2和1E 对应的吸收波长为1042 nm,跃迁时不会辐射产生波长637—750 nm 的荧光光子.NV 色心处于不同的自旋态时,两种过程发生的概率不同.相比于处于|ms=0〉态,NV 色心处于|ms=±1〉态时通过ISC过程从激发态回到基态的概率更大.在ISC 过程中,NV 色心从激发态3E 跃迁到自旋单态1A2,再到1E ,最后回到基态3A2.当NV 色心从自旋单态1E 跃迁到三重态的3A2时,落在|ms=0〉能级和|ms=±1〉能级上的概率相当[14].NV 色心在基态和激发态往返多个周期后,|ms=±1〉能级上的布居度逐渐转移到|ms=0〉上.当施加一束532 nm 激光时,处于|ms=0〉态的NV 色心被激发后通过辐射跃迁过程回到基态的概率更大,在637—750 nm波段产生的荧光光子数比处于|ms=±1〉态时更多,因此实验上可以通过荧光强度来区分NV 色心的电子自旋状态.同时随着时间推移|ms=±1〉能级上的布居度越来越小,最终电子自旋被极化到|ms=0〉态,室温下极化率能达到95%以上[15].这样通过激光就实现了对NV 色心电子自旋的初始化和量子态读出.

2.2 NV 色心的自旋量子控制

其中ω0=D-ωe是量子比特的共振频率;ω1,ωMW,ϕ分别是微波脉冲的幅度、频率和相位.选取旋转坐标U=e-i2πωMWtSz,实验中所加微波场满足旋波近似条件ω1≪ωMW,故旋转坐标系内哈密顿量可以化简为

该哈密顿量下的演化算符为U=e-iHrott(取自然单位制 ℏ =1).通过调节微波脉冲的频率ωMW、幅度ω1、相位ϕ和时长t,就可以实现Bloch 球中任意的旋转操作R(),从而实现电子自旋量子比特的普适量子控制.同样地,对于核自旋量子比特,可以用射频脉冲实现普适的量子控制.对于NV 色心电子自旋和核自旋组成的两比特量子系统,利用电子自旋和核自旋间固有的耦合,通过微波和射频脉冲可以实现的普适量子控制.

3 NV 色心体系的退相干

上面的讨论中没有考虑环境的作用,把NV 色心看作一个理想的封闭系统.而实际上任何物理体系都不可避免地与环境发生相互作用,在环境噪声的影响下量子态会逐渐弛豫到环境温度下的热平衡态.NV 色心的环境噪声主要来源于和自旋热库及声子的相互作用,其弛豫过程可以唯象地看成同时发生的两个过程[16].一个是自旋角动量纵向分量的平均值〈Sz〉从初始值逐渐演化到热平衡态对应值的过程,称为纵向弛豫,用纵向弛豫时间T1来表征.纵向弛豫和自旋态翻转有关,主要来自于电子自旋与声子之间的相互作用.而电子自旋与自旋热库的耦合强度远小于其能级差,自旋热库对纵向弛豫过程的贡献可以忽略不计.在室温下金刚石中声子激发很弱[17],NV 色心的纵向弛豫过程受到抑制,T1长达毫秒量级.另一个过程是自旋角动量的横向分量平均值〈Sx〉和〈Sy〉逐渐衰减到零的过程,称为横向驰豫,用退相干时间T2和退相位时间T2*表征,二者分别对应不同的弛豫机制.横向弛豫主要来自于NV 色心电子自旋与周围大量电子自旋和核自旋(自旋热库)的相互作用.当不考虑环境噪声时自旋量子态会在外加静磁场的作用下绕Bloch 球中z轴以拉莫频率ωe=γeB0进动.自旋热库的作用相当于在每次实验中沿主轴方向附加一个随机的局域磁场,从而每次实验拉莫进动频率有细微的不同,一定时间内积累的相位不再是定值,而是满足一定的分布.这样多次实验后〈Sx〉和〈Sy〉因为平均效应发生衰减,并且随时间积累逐渐趋于零.这个随机的局域磁场称为Overhauser 场,它导致的拉莫频率偏差记为δ0.Overhauser 场中准静态成分引起的弛豫过程,称为退相位过程,由退相位时间描述.在退相位过程中局域磁场是准静态的,δ0在单次实验中保持不变,在多次实验中满足高斯分布.图3(a)是实验测得的退相位过程作用下电子自旋的自由感应衰减(free induction decay,FID)曲线,插图是实验测量的微波脉冲序列—拉姆齐序列(Ramsey sequence)[18].图中红点为实验数据点,误差棒为实验统计标准差.黑色实线是对实验数据的拟合结果,黑色虚线为其对应的包络线.根据准静态噪声模型拟合,可以得到退相位时间=1.68(3) µs 以及对应的δ0分布,结果如图3(b)所示.

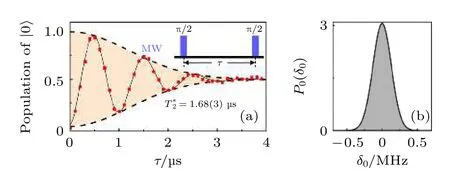
图3 NV 色心电子自旋的退相位过程[18] (a) 电子自旋的自由感应衰减曲线,插图为实验脉冲序列;(b) 准静态噪声 δ0 的分布 P (δ0)Fig.3.Dephasing process of the electron spin of the NV center[18]:(a) FID of the electron spin,the inset is the experimental pulse sequence;(b) probability density distribution of δ0 .

在拉姆齐序列中t=τ/2 位置插入一个 π 脉冲,则得到Hann 回波序列.施加Hann 回波序列后量子态在脉冲前半段积累的相位与后半段积累的相位相互抵消,从而消除了单次实验中准静态噪声δ0带来的影响.这时测得的相干衰减,主要来源于Overhauser 场的非准静态部分,即每次实验中局域磁场的动态涨落.这个退相干过程由T2表征.T2一般在百微秒到毫秒量级,远长于=1.68 µs.这说明Overhauser 场在单次实验中动态涨落很小,NV 色心的退相干主要来自每次实验中准静态噪声δ0的差异.

要实现对NV 色心电子自旋的量子控制,需要施加微波脉冲.因此除了NV 色心本身的环境噪声外,还存在操控场噪声,主要考虑操控场强度涨落δ1带来的噪声.一般在量子控制的时间尺度内操控场涨落很小,因此可以将操控场噪声δ1看作准静态的,且通常认为δ1满足洛伦兹分布[19].实验上通过测量拉比振荡衰减可以确定准静态操控场的涨落分布.图4(a)是实验测得的电子自旋拉比振荡衰减曲线,图中绿点、黑色实线和虚线分别是实验数据点、对实验点的拟合和拟合曲线的包络,插图为实验测量的微波脉冲序列.根据准静态操控场噪声模型对实验数据拟合,得到特征时间=73(7) µs以及δ1的分布如图4(b).

图4 操控场噪声下NV 色心的退相干[18] (a) 电子自旋的拉比振荡,插图为实验脉冲序列;(b) 准静态操控场噪声δ1 的分布 P (δ1)Fig.4.Decoherence of the NV center under control field noise[18]:(a) Results of the nutation experiment for the electron spin,the inset is the experimental pulse sequence;(b) probability density distribution of δ1 .

实验选取的NV 色心的T1在毫秒量级,T2在百微秒到毫秒量级,,分别为1.68 µs 和73 µs.从它们的相对大小可以看出,量子控制中主要噪声来自于准静态环境噪声δ0和操控场噪声δ1.如果能对这两类噪声加以抑制,就能够极大地延长量子态的相干时间,实现高精度的量子控制.

4 单自旋量子控制的应用

经过多年的实验研究发展,基于金刚石NV 色心体系的量子控制技术已经相当成熟,不仅能将普适量子逻辑门保真度提高到容错量子计算的阈值,还能对时间最优问题和可编程量子控制进行深入的研究.同时,对于新兴的研究领域比如非厄米物理,在NV 色心体系上也能实现普适的非厄米量子控制.本节将介绍基于NV 色心体系的量子控制研究进展和应用,包括动力学纠错门[20]、单比特和两比特的容错量子逻辑门[18]、时间最优量子控制[21]、可编程量子控制[22]和基于宇称时间对称哈密顿量的量子控制[23].

4.1 动力学纠错门

早期研究中,常通过动力学解耦序列[24—28](如前文的Hann 回波序列)来延长量子态的相干时间,所能达到的相干时间极限为T1ρ[29].之后动力学解耦被用作保护量子逻辑门[15,30,31],通过量子逻辑门控制序列和动力学解耦序列的巧妙结合,在实现目标量子控制的同时抑制环境噪声.但这种方法原则上要求解耦脉冲的强度无限大,而实际物理体系中操控强度总是有限的.因此有研究工作基于有限操控强度设计了抑制环境噪声的量子逻辑门序列,即动力学纠错门[32—36].

在各种动力学纠错门中,研究者发现一类称为SUPCODE (soft uniaxial positive control for orthogonal drift error)的脉冲序列,能够有效抑制NV 色心中磁场涨落和自旋热库耦合带来的准静态噪声δ0[28].SUPCODE 序列由不止一段脉冲组成,调节每段脉冲的幅度、相位和时长等参数,能够像Hann 回波序列一样使前后脉冲中准静态噪声带来的偏差相互抵消,从而抑制准静态噪声引起的退相干,提高量子逻辑门保真度.下面以量子逻辑门为例说明SUPCODE序列对准静态噪声的抑制效果[20].考虑环境噪声强度δ0远小于脉冲操控强度ω1,通过计算可知,对于普通方波脉冲,准静态噪声对量子逻辑门保真度的影响是二阶的;对于由三段脉冲组成的3-piece SUPCODE 序列,准静态噪声对保真度的影响是四阶的;而由五段脉冲组成的5-piece SUPCODE序列,能够将准静态环境噪声对量子逻辑门保真度的影响抑制到六阶[20].如果想抑制更高阶的噪声,则序列需要更多段的脉冲提供足够的参数自由度来消除更多的噪声高阶项.理论上通过不断增加SUPCODE 序列的脉冲段数,可以将准静态环境噪声对量子逻辑门的影响抑制到任意高阶.

研究者利用NV 色心体系,通过调节微波偏共振模拟准静态环境噪声δ0,研究和验证了SUPCO DE 序列实现的量子逻辑门保真度与δ0的关系[20].具体实验过程如下:首先将NV 色心电子自旋量子比特初始化到|0〉态,然后分别施加量子逻辑门为R(π)的普通方波脉冲、3-piece SUPCODE 脉冲序列和5-piece SUPCODE 脉冲序列,最后测量在不同环境噪声δ0/ω1下的末态保真度偏差δf=1-理论计算表明,末态保真度的偏差随δ0/ω1的阶数关系(表1)与量子逻辑门保真度的阶数一致,因此可以用末态保真度来衡量对应δ0噪声下量子逻辑门保真度.

表1 不同量子逻辑门序列下末态保真度的偏差随 δ0/ω1 的阶数关系[20]Table 1.Infidelity of quantum gate for different pulses as a function of δ0/ω1 [20].

实验中设置微波偏共振从1.5 MHz 到6 MHz.由拉姆齐脉冲实验和拉比振荡实验结果,得到准静态环境噪声δ0和操控场噪声δ1分布的线宽分别为0.03 MHz 和0.11 MHz,均远小于微波偏共振.因此可以认为实验中的噪声主要来自偏共振模拟的准静态环境噪声δ0.测得不同脉冲序列下末态保真度偏差随准静态噪声δ0变化如图5 所示,图中实线对应表1 中的理论计算结果,灰色虚线代表实验数据的不确定度水平.在误差范围内,实验数据与理论吻合,证明了普通方波脉冲、3-piece 和5-piece SUPCODE 脉冲序列分别将准静态噪声δ0对量子逻辑门保真度的影响抑制到了二阶、四阶和六阶.

图5 实验验证SUPCODE 序列在实现量子逻辑门时对准静态环境噪声的抑制效果[20]Fig.5.Experimental demonstration of the robustness of SUPCODE against the noise stemming from the quasistatic fluctuation of Overhauser field[20].

保真度是衡量量子控制准确性的一个重要指标.5-piece SUPCODE 序列实现的量子逻辑门的保真度很高,实验上难以直接地精确测量,但可以通过级联的方式间接得到.5-piece SUPCODE 序列实现的量子控制可以看作理想量子逻辑门演化的同时进行特征时间T1ρ的弛豫过程.由于SUPCODE 序列时间为τp=5.06 µs,远小于弛豫时间T1ρ,两个过程可以认为相互独立,即量子态先进行理想量子逻辑门演化再进行相同时长的弛豫.T1ρ弛豫过程可以用退极化通道描述εD(ρi)=pI/2+(1-p)ρi,其中,为单个5-piece SUPCODE 序列的时间内T1ρ弛豫导致量子态发生错误的概率.级联M个5-piece SUPCODE 序列对应量子逻辑门保真度为实验上通过量子过程层析技术[37]确定级联M个5-piece SUPCODE 序列在泡利基下的过程矩阵,利用过程矩阵计算得到量子逻辑门保真度如图6.图中M分别取0,27,54,81,108,135,黑色实线为理论给出保真度FM与M个序列总时间T=Mτp的关系,灰色区域为T1ρ的测量不确定度导致的不确定区域.可以看出,实验结果与理论符合的很好.由此模型计算,取M=1 得到单个5-piece SUPCODE 序列实现的量子逻辑门保真度为0.9961(2).

图6 级联5-piece SUPCODE 序列实现的量子逻辑门保真度随序列时长的关系[20]Fig.6.Decay of the fidelity of 5-piece SUPCODEs[20].

4.2 普适容错量子逻辑门

和经典计算机一样,量子计算过程中量子比特会受到退相干噪声、操控测量噪声等因素影响发生错误.为了保障计算结果的可靠性,需要相应的纠错手段.仿照经典纠错码在编码时引入冗余的思路,如果用多个物理的量子比特编码成一个逻辑量子比特,利用物理比特之间的关联来检测并纠正错误,就可以将量子计算出错的概率降到任意低,实现容错量子计算.容错量子计算的首要条件是实现达到容错阈值的高保真度量子逻辑门.因为在纠错时要对物理量子比特进行一系列操作,如果量子逻辑门的保真度低于容错阈值,不仅达不到纠错的目的,还可能引入额外的错误.动力学纠错门能有效抑制量子逻辑门过程中的准静态环境噪声δ0,实现保真度为0.9961 的单比特量子逻辑门.然而量子逻辑门的保真度不仅受限于环境噪声δ0,还受限于操控场噪声δ1.要实现更高的量子逻辑门保真度,就需要同时抑制这两类噪声.本节展示了单比特容错量子逻辑门和两比特容错CNOT 门的设计方法和实验结果.

图7 以量子逻辑门R(xˆ,π/2) 为例展示了不同脉冲序列对环境噪声δ0和操控场噪声δ1抑制效果[18].每个子图的下半部分为不同准静态环境噪声δ0和操控场噪声δ1下的量子逻辑门保真度,黑色实线为保真度0.9999 的等值线.子图上半部分为对应脉冲序列,其中上下两行代表各段脉冲的相位和转过的角度.可以看出,对于普通方波脉冲(图7(a)),仅原点附近很小的一块区域保真度大于0.9999.这是因为普通方波脉冲对准静态环境噪声δ0和操控场噪声δ1并没有特别的抑制效果,二者对于保真度的影响都是二阶的.而5-piece SUPCODE 脉冲序列(图7(b)),能够将δ0对保真度的影响抑制到六阶.因此图中黑色实线围成的区域沿δ0方向扩大,但在δ1方向是比图7(a)中普通方波脉冲对应的区域还要小.这说明5-piece SUPCODE 脉冲序列虽然能很好地抑制准静态环境噪声δ0,但受操控场噪声δ1影响比普通方波脉冲还大.

图7(c)展示的是一种常用的能抑制操控场噪声δ1的量子逻辑门的脉冲序列—BB1 (broadband number 1)脉冲序列[38].BB1 脉冲序列可以将δ1对保真度的影响抑制到六阶,但δ0的影响仍是二阶的.图7(c)中保真度大于0.9999 的区域沿δ1方向显著增大,但在δ0方向的增大并不明显,表明BB1序列对δ0的抑制并不理想.

图7 实现量子逻辑门的各种脉冲序列及在噪声影响下的保真度[18] (a) 普通方波脉冲;(b) 5-piece SUPCODE 脉冲序列;(c) BB1 脉冲序列;(d) BB1inC 脉冲序列Fig.7.Pulse sequences for quantum gate and the fidelity under noises[18]:(a) Plain pulse;(b) 5-piece SUPCODE pulse;(c) BB1 pulse;(d) BB1inC pulse.

上述几种脉冲序列都只能抑制δ0或δ1.想要实现对δ0和δ1的同时抑制,需要设计新的量子逻辑门脉冲序列.一个基本的思路是,基于已有的SUP CODE 和BB1 等能单独抑制某项噪声的脉冲序列,将能抑制δ0的脉冲序列与能抑制δ1的脉冲序列以嵌套的方式组合[39,40].脉冲序列的嵌套,指对于一个由多段方波脉冲组成的脉冲序列Aseq,每段脉冲对应的量子操作用脉冲序列Bseq而不是普通方波脉冲来实现,得到的新脉冲序列记为BseqinAseq.脉冲序列Bseq称为内嵌序列,脉冲序列Aseq称为外套序列.然而,将任意一个能抑制δ0的序列和一个能抑制δ1的序列嵌套,并不能保证新脉冲序列同时抑制δ0和δ1.比如,将5-piece SUPCODE 序列嵌套在BB1 序列中,得到的序列却不能保留BB1 序列抑制δ1的特性,δ1对保真度的影响依然是二阶的;而如果将BB1 序列嵌套在5-piece SUPCODE 序列中,新序列能同时将δ0和δ1对量子逻辑门保真度的影响抑制到四阶.

研究者尝试了多种不同外套和内嵌序列的嵌套方案,在保证同时抑制δ0和δ1的前提下,使高保真度区域尽可能大,以保证实现的量子逻辑门保真度尽可能高.最终选择将BB1 序列作为内嵌序列嵌套到CORPSE 序列中,得到BB1inC 序列(图7(d)).CORPSE 序列是一种能够抑制δ0的量子逻辑门组合脉冲[41],δ0和δ1对其保真度的影响分别是四阶和二阶.与图7(a)的普通方波序列相比.图7(d)中BB1inC 脉冲序列对应的高保真度区域在δ0和δ1方向上都增大了很多.

实验上通过测量量子逻辑门保真度来验证各脉冲序列对于噪声的抑制效果.由于待测逻辑门保真度都很高,测量时受初态制备误差和测量误差的影响较大.因此采用不受初态制备和测量误差的影响的RB (randomized benchmarking)方法对高保真度进行精确测量[42].测量时先将量子比特初始化到|0〉态,然后施加若干个随机的量子门计算单元.每个量子门计算单元包括一个从泡利群中随机选取的泡利门和从克利福德群中选取的非泡利克利福德门,计算单元中的量子逻辑门由待测的脉冲序列实现.最后测量末态保真度.因为量子门计算单元中的泡利门和克利福德门是随机选取的,所以需要重复多次实验取保真度的平均值.对于由n个量子门计算单元组成的序列,当重复次数足够多时,末态平均保真度F¯ 与量子门计算单元个数n满足其中d与初态制备和测量误差有关,ε为单个量子逻辑门的平均出错概率.实验上通过测量末态平均保真度随n的关系并根据上式拟合,可以得到量子逻辑门的平均出错概率ε,则待测量子逻辑门的平均保真度为Fa=1-ε.

图8 是用RB 方法对上面四种脉冲序列实现的单比特量子逻辑门保真度测量的实验结果[18].图中深蓝色正方形、绿色三角、蓝色圆形和红色菱形分别为普通方波脉冲、5-piece SUPCODE 脉冲序列、BB1 脉冲序列和BB1inC 脉冲序列对应的实验结果,实线为对四组实验数据的拟合结果,拟合得到的量子逻辑门的平均出错概率ε画在插图中.根据拟合结果,5-piece SUPCODE 脉冲序列实现的量子逻辑门平均保真度为0.99916(8),低于普通方波脉冲对应的平均保真度0.99968(6).这说明实验中相较于环境噪声δ0,操控场噪声δ1占主导,而5-piece SUPCODE 脉冲序列对δ1的抑制效果不如普通方波脉冲,所以保真度更低.当施加能够抑制δ1的BB1 脉冲序列时,量子逻辑门的平均保真度显著提高,达到0.999945(6),这也说明了δ1噪声是量子逻辑门出错的主要因素.BB1inC 脉冲序列因为能同时抑制δ0和δ1,量子逻辑门的平均保真度相较于BB1 序列也有所提升,为0.999952(6),达到了容错量子计算对保真度的阈值要求[43],代表了目前固态自旋体系单比特量子逻辑门保真度的最高水平.

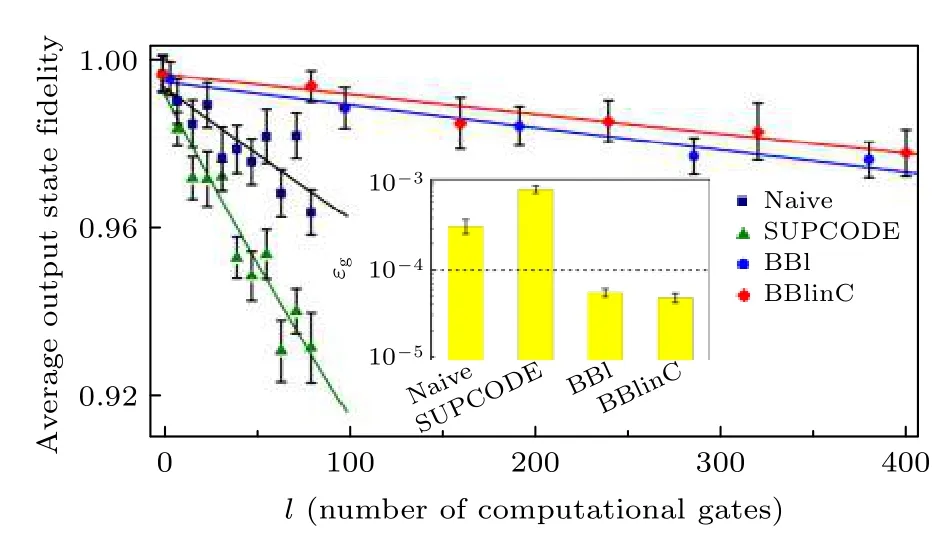
图8 单比特量子逻辑门保真度的实验测量结果,插图为四种脉冲序列对应的量子逻辑门的出错概率 ε [18]Fig.8.Average fidelity of single-qubit gates,where the inset shows the average error per gates of the pulses[18].

想要实现普适的容错量子控制,除了一组普适的单比特量子逻辑门外,还需要一个非平庸的两比特量子逻辑门,实验中选的是两比特CNOT 门.为了提高两比特CNOT 门的保真度达到容错阈值,通过改进的梯度上升算法优化组合脉冲中的参数,使得在δ0和δ1影响下高保真度区域尽可能大.在确定各段脉冲的参数后,通过图9(a)所示的量子线路图测量连续施加N个CNOT 门,得到末态在|0,1〉上的布居度与N的关系如图9(b),其中N取偶数[18].理想情况下布居度应该恒为1,但在δ0和δ1影响下末态布居度会随N增大不断衰减.而布居度的振荡来自于实际实现的CNOT 门与理想CNOT 门的偏差.图中蓝色虚线是只考虑δ0和δ1分布的拟合结果,与实验数据偏差较大.这是因为拟合使用的超精细耦合强度A和共振频率Ω都是通过实验测量得到的,与实际值存在一定的偏差.将偏差 δA和 δΩ作为参数重新拟合,得到红线与实验结果符合的很好,对应的CNOT 门平均保真度为0.9920(1),达到了容错阈值.

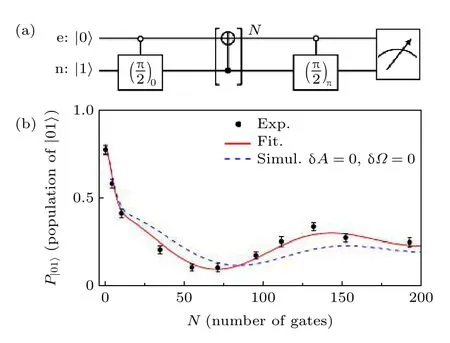
图9 测量CNOT 门保真度的量子线路图(a)和实验结果(b)[18]Fig.9.Quantum circuit diagram (a) and experimental result (b) for measuring the fidelity of CNOT gates[18].

4.3 时间最优量子控制

在量子控制中不可避免地会受到各种噪声的影响,第4.2 节展示了通过优化组合脉冲对抗噪声的方法能够实现高精度的量子控制.从另一个角度出发,如果能实现时间最优控制即在最短的时间内完成量子控制,不仅能在有限的相干时间内进行更多的量子操作,还能减少量子系统与环境作用的时间,提高量子控制的精度.与针对性的抑制噪声方法不同,时间最优量子控制不需要预先知道噪声相关的信息,能普适地提高量子逻辑门保真度.

量子领域的时间最优控制问题,指在系统操控强度和哈密顿量受限的情况下,如何在最短时间内实现特定的量子控制.如图10,类比于Zermelo 的导航问题[44],对于给定的目标量子操作UF,有很多条路径使演化算符从初始时刻的U(0)=I变到U(T)=UF,每条路径对应一个含时哈密顿量[21].而量子操控强度有限对应导航问题中的航速有限,哈密顿量受限在某个子空间意味着路径不能任意选取.时间最优量子控制就是从中找出时间T最短的一条路径.经典理论中对时间最优控制比如最速降线问题有比较深入的研究,量子控制领域也有量子最速降线方程,通过求解量子最速降线方程即可得到相应时间最优量子控制.然而对于两比特系统乃至更高维的情况,量子最速降线方程并没有有效的求解方法.直到2015 年有研究者提出了测地线方法[45],能对多比特系统的量子最速降线方程进行有效的数值求解.利用这种方法在金刚石NV色心体系上首次实现了两比特时间最优控制[46].

图10 时间最优控制示意图[21]Fig.10.Schematic diagram of time optimal quantum control[21].

图11 是利用NV 色心体系实现单比特最优控制的实验结果,红色代表时间最优量子控制,蓝色代表利用欧拉转动实现的量子控制[21].从图11(a)可看出,对于Bloch 球中绕z轴的转动操作,由于实验中哈密顿量受限,欧拉转动消耗的时间确实比时间最优控制所消耗的时间更多.时间最优控制和欧拉转动实现量子控制的路径可以通过图11(b)给出的〈Sy〉和〈Sz〉随时间的关系来展示.

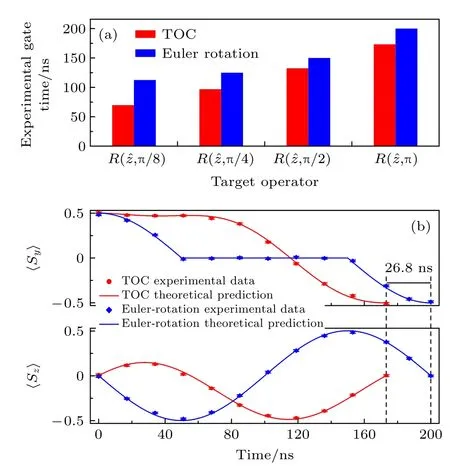
图11 时间最优量子控制和欧拉转动实现单比特操控R(,θ) 花费时间对比[21] (a) 转角 θ 分别为 π/8 ,π/4 ,π/2和 π 时,实现单比特操控 R (,θ) 耗时对比;(b) 时间最优量子控制和欧拉转动下量子态的演化过程Fig.11.Comparison on time costs for target gate operator R(,θ)between the derived time-optimal control (TOC)and the Euler rotations[21]:(a) Comparison of experimental gate time for θ =π/8 ,π/4 ,π/2 ,and π ;(b) state evolutions during R (,θ) with TOC and Euler rotation.

对于两比特的情况,选取受控操作U(T):当核自旋处于mI=|1〉时,电子自旋保持不变;当核自旋处于mI=|0〉时,对电子自旋做σy操作.利用选择性脉冲实现U(T)所花费的时间为612.4 ns,而通过测地线方法求解量子最速降线方程,得到的时间最优控制脉冲序列总时长为446.1 ns,比选择性脉冲短166.3 ns.图12(a)和图12(b)分别展示了在mI=|1〉和mI=|0〉子空间内电子自旋初态为|0〉时量子态在时间最优控制下的演化路径,左图是Bloch 球上的演化轨迹,右图是对应子空间内电子自旋布居度随时间的变化[21].可以看出,在mI=|1〉子空间内,电子自旋量子态沿一条曲折的路径最终回到了初始位置;而在mI=|0〉子空间内电子自旋状态发生了翻转,这与预期的受控操作U(T)是一致的.为了检验时间最优控制对噪声的抑制效果,利用量子层析技术测出两比特时间最优控制的保真度为0.99(1),同样达到了容错量子计算的阈值.在NV 色心上首次实现的两比特时间最优控制,不仅验证了多比特时间最优控制的可行性,还提供一种提高量子逻辑门保真度的普适方法.

图12 初态为(a) | 0,1〉和 (b) | 0,0〉时量子态在两比特时间最优控制下的演化[21]Fig.12.State trajectories under the two-qubit controlled-U gate by TOC with initial states (a) | 0,1〉 and (b) | 0,0〉 [21].

4.4 可编程量子控制

在经典计算机中,硬件单元和它能实现的操作是固定的,却能通过软件编程实现各种算法完成不同的功能,这就是可编程控制的概念.同样地,人们希望实现通用量子计算机,能在不改变物理硬件的前提下通过可编程量子控制实现各种量子算法.然而理论上已经证明不存在完全量子的确定性的可编程量子器件[47].对于概率性的可编程量子器件[48,49],每次量子控制的成功概率小于1,且需要通过测量并进行后选择操作才能判断是否成功实现目标量子控制.而一个大型的量子线路由很多可编程器件组成,导致整个计算成功的概率趋于零而难以实际应用.于是研究者采用与经典计算机结合的方法,利用普适的量子线路图,将量子算法分解成由一系列量子逻辑门,把量子操作编码成量子逻辑门脉冲序列的时间、幅度、相位等参数,通过经典计算机输入这些经典参数来施加不同的量子控制以完成相应的量子算法.利用这种方法在NV 色心体系上实现了两比特可编程量子处理器[22],为将来大规模的可编程量子计算打下了基础.

任意的量子算法都可以表示成普适的量子线路图,用一组量子逻辑门实现.根据具体物理体系能实现的量子逻辑门集合,选择合适的量子线路图,就能将一个完整的量子算法编码成一系列的参数.对于两比特的情况,单比特门和一个非平庸的两比特门就可以实现普适的量子控制.具体而言,一个任意两比特量子逻辑门可以分解为3 个CNOT门和15 个从集合{Rx,Rz}中选取的单比特门[50].在NV 色心体系中,实现两比特操作比CNOT 门更方便.因此用Uzz门代替CNOT 门,而单比特门可以从集合{Rx,Ry,Rz}中选取,得到两比特普适量子线路如图13[22].任意的两比特操作U可以作分解U=(C ⊗D)·V ·(A ⊗B),由3 个Uzz门和12 个单比特门组成,总共包含15 个可调的参数.

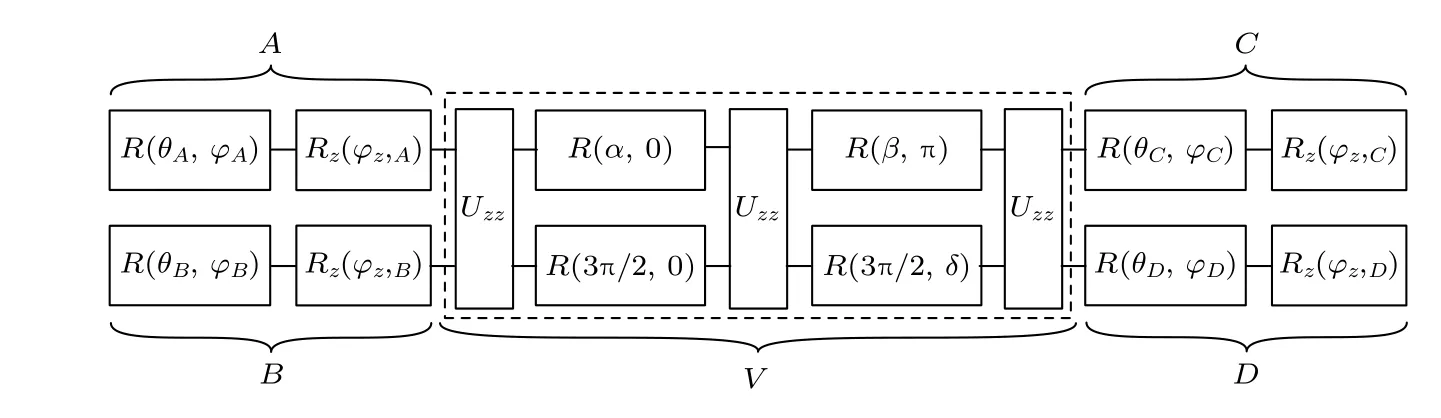
图13 普适可编程量子逻辑线路[22]Fig.13.Universal programmable quantum logic circuit[22].

量子线路图中的单比特门可以用图14 中的脉冲实现[22].对于电子自旋比特,一段相位为ϕ,幅度为ω1,持续时间t=θ/ω1的微波脉冲就可以实现单比特量子操作R(θ,ϕ) .由于核自旋和电子自旋的超精细耦合,核自旋状态不同时,电子自旋的共振频率有一定的差别,因此要求对电子自旋施加的微波脉冲幅度远大于超精细耦合常数,使得微波脉冲实现的量子操作与核自旋状态无关.而对于核自旋比特,由于核自旋的相干时间比电子自旋大3 个数量级,在操控核自旋时电子自旋会发生退相干.因此实验中采用退相干保护逻辑门的方法,施加图14(b)所示的XY-4 序列来保护电子自旋的相干,在XY-4 序列脉冲的间隙内施加射频脉冲,对核自旋实现不依赖电子自旋的单比特操作R(θ,ϕ) .

图14 单比特门对应的脉冲[22]Fig.14.Realization of the single-qubit gate[22].

利用普适量子线路图,在由NV 色心构建的两比特可编程量子处理器上,只需要修改脉冲参数就能实现任意的两比特量子算法,在该平台上演示的两个典型量子算法:Deutsch-Jozsa 算法和Grover搜索算法,成功率都超过80%[22].

4.5 宇称时间对称哈密顿量的量子控制

量子力学中基本假设要求可观测量用厄米算符表示,系统的哈密顿量算符也不例外.哈密顿量的厄米性保证了系统的本征能量为实数,但是对于某些非厄米哈密顿量比如宇称时间(PT)对称哈密顿量,在对称非破缺的情况下也具有实的能量本征值[51].于是人们尝试将量子力学基本假设中的厄米性条件推广为PT对称条件,以此为基础建立PT对称量子力学.相关理论可以参考文献[52-56].下面简单介绍背景知识.

PT对称哈密顿量指满足对易关系[HP T,PT]等于0 的哈密顿量HP T.其中P,T为宇称算符和时间反演算符,二者是四阶反演群的生成元,满足P2=T2=I,[P,T]=0.由于时间反演算符T是反线性算符,虽然哈密顿量HP T与PT算符对易,但二者并不一定具有共同本征态.考虑一个简单的两能级PT对称系统的哈密顿量:

其中r是实参数,二维希尔伯特空间中P,T算符表示为

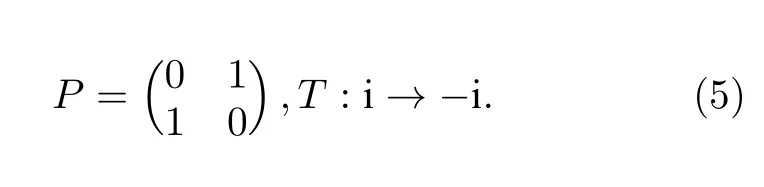
可以验证HPT与PT算符对易.HPT的本征能量为当参数|r|＜1时,本征能量为实数,哈密顿量与PT算符有共同本征态,称为PT对称非破缺.特别地,当r=0 时,哈密顿量是厄米的,两个本征态正交.而当哈密顿量是非厄米即r/=0 时,两个本征态不相互正交.当参数|r|＞1 时,本征能量为虚数,哈密顿量与PT算符不再有共同本征态,称为PT对称破缺.PT对称非破缺区域和破缺区域的交界点|r|=1 称为奇异点.在PT对称非破缺区域,当r从0 开始逐渐趋近于奇异点|r|=1 时,两个实本征值大小逐渐接近,直到|r|=1处完全简并,此时本征态也发生简并.当|r|进一步增大,PT对称性发生破缺,本征值变为一对共轭的虚数.PT对称系统由于存在奇异点这一特殊的拓扑结构以及传统厄米系统中没有的新奇物理现象,如非厄米系统的体边对应关系[57]、非厄米趋肤效应[58]、非厄米拓扑相[59]等,引起了研究者们的广泛关注.然而通常量子体系都是厄米的,在其中实现PT对称哈密顿量并不容易.因此,早期的实验研究主要是用经典光学体系,通过引入耗散或者增益来模拟薛定谔方程下PT对称哈密顿量的演化[60,61].除了光学体系,在电路[62—64]、微波[65]、力学[66]和声学[67—69]等经典体系中都实现了对PT对称哈密顿量的模拟研究.尽管在经典体系的模拟研究能很好地展示PT对称哈密顿量的物理性质,但想要更深入地研究PT对称哈密顿量尤其是奇异点附近的奇特性质,需要在实际的量子体系中真正实现PT对称哈密顿量.

2019 年有研究者提出了一种在量子系统中实现PT对称哈密顿量的普适方法,并且在金刚石NV 色心系统上进行了实验验证,首次在单自旋体系中实现了量子态在PT对称哈密顿量下的演化,观测到PT对称破缺现象[23].同期在冷原子系综体系[70]以及超导量子体系[71]中也实现了PT对称哈密顿量,然而二者都是通过引入耗散实现PT对称哈密顿量的.耗散会极大地破坏量子态的相干,严重局限了这种方式在非厄米相关领域研究中的应用.而在NV 色心体系上的实现方法是通过引入一个辅助比特,将PT对称哈密顿量HP T扩展为一个厄米哈密顿量Hs,a(t),然后选取厄米系统的一个子空间,使子空间中量子态满足非厄米哈密顿量的演化规律.可以证明,这种方法是普适的,从PT对称非破缺区域到PT对称破缺区域、乃至任意非厄米哈密顿量,从不含时到含时哈密顿量,都可以通过一个辅助比特实现,且不会破坏量子系统的相干性.这对于含有多重简并的高阶奇异点,以及奇异点附近的拓扑性质和动力学性质的研究具有突破性的意义.

根据这种扩展的方法,(4)式中的非厄米哈密顿量可以扩展为两比特的厄米哈密顿量Hs,a(t)=其中Ai(t)(i=1,2,3,4) 是展开系数.为了在金刚石NV 色心实现该哈密顿量,选取电子自旋为系统比特,核自旋为辅助比特,并施加两路选择性的微波脉冲.通过控制两路微波脉冲的幅度、频率、相位来实现对应哈密顿量演化,最后对辅助比特沿σy本征态测量并选取的测量结果,对应电子自旋演化即为PT对称哈密顿量HP T下的演化.图15 为对应量子线路图[23].

图15 金刚石NV 色心体系中实现PT 对称哈密顿量的量子线路图[23]Fig.15.Quantum circuit of the experiment of constructing a PT symmetric Hamiltonian in a NV center[23].

图16(a)—图16(d)分别展示了NV 色心体系中量子态在厄米哈密顿量、PT对称非破缺区域、奇异点处和PT对称破缺区域的演化[23].红色实线为理论预期,蓝色圆点为实验结果.可以看出,当系统哈密顿量位于PT对称非破缺区域时,量子态以一定周期在|0〉态和|1〉态之间振荡.随着参数r从0 逐渐增大趋向于1,哈密顿量由厄米趋向于奇异点,振荡的周期不断变长.在奇异点处,量子态演化不再呈现周期性振荡,而是单调衰减并最终趋向于稳态.在PT对称性破缺区域,随着r继续增大,量子态衰减趋向于稳态的速率越来越快.如果对测得的量子态演化曲线与理论计算相拟合,可以得到PT对称哈密顿量能量本征值随参数r的关系,与理论预言的一样.随着参数r的增大,能量本征值从实数逐渐趋于0,在奇异点发生简并,再发生PT对称破缺变为纯虚数.图16 确实地从实验上观测到了PT对称哈密顿量破缺的过程和奇异点的存在.

图16 量子态在PT 对称哈密顿量 H P T 下的演化[23] (a) r =0,厄米哈密顿量;(b) r =0.6,PT 对称非破缺;(c) r =1.0,奇异点;(d) r =1.4,PT 对称破缺时的情况Fig.16.State evolution under H P T [23].Experimental dynamics of renormalized population P0 when r =0 (a),r =0.6 (b),r =1.0 (c),and r =1.4 (d).

5 总结与展望

本文主要从实验角度出发,介绍了NV 色心体系的能级结构和量子控制原理,详细阐述了NV 色心的退相干机制和通过抑制退相干效应来提升量子控制精度的各种方法,以及应用NV 色心量子控制技术在量子物理领域取得的研究成果.

经过多年的实验研究和发展,对于NV 色心体系的量子控制已经达到相当高的精度,不仅能够实现高保真度的普适容错量子逻辑门和时间最优量子控制,还能构建可编程的量子处理器,这都为未来实现室温下大规模的可编程量子计算打下了坚实的基础.同时,对于新兴的物理领域如非厄米物理,在NV 系统上也可以通过扩展的方法对非厄米量子体系中新奇的物理现象[72]进行观测和研究.除此之外,NV 色心对磁场、电场、温度等物理量都十分敏感,通过精确的量子控制可以利用NV 色心作为纳米尺寸的探针,对各种微小信号进行精密测量.而非厄米系统中的奇异点,对于参数变化具有放大作用,因此可以用于进一步提高量子精密测量的灵敏度[73,74].这种纳米尺度的高灵敏量子传感器,在生物、化学等领域有着广泛的应用前景和巨大的潜力.