高压大功率晶闸管反向恢复物理过程建模与计算*
2021-05-24刘隆晨李亚伟喻悦箫陈少卿曹运龙
刘隆晨,李亚伟,喻悦箫,陈少卿,曹运龙
(国网四川省电力公司 a. 电力科学研究院,b. 检修公司,成都 610072)
超特高压直流输电凭借在远距离大容量输电以及电网互联等方面的优势在我国电力输送领域中发挥着重要作用,当前直流输电普遍采用晶闸管换流阀[1-2].晶闸管是直流输电换流阀的核心器件,利用晶闸管的开关特性,换流阀才能完成其作为输电“高压开关”的功能.随着电力电子技术的迅速发展,单个晶闸管通断能力也不断增强[3].
晶闸管反向恢复特性主要由关断过程中晶闸管内部过剩载流子的转移引起,其对换流阀开通暂态特性具有重要影响[4-6].岳珂等[7]通过将反向恢复电流等效为解析电路模型研究了晶闸管阀关断过程中电压分布情况;孙玮等[8]研究了反向恢复特性分散性对串联晶闸管换流阀电压分布、最小触发电压以及最小关断角的影响;黄华等[9]基于反向恢复电荷特性数据,采用电路解析计算的方法研究了故障电流下换流阀的反向电压特性.国内外研究人员对晶闸管反向恢复特性和换流阀工作特性的研究多从器件或阀体设计的角度出发,多采用半理论模型描述器件工作特性,存在计算过于简单,无法正确反映晶闸管反向恢复物理过程的内部微观情况等缺点[10-12].因此有必要借助半导体物理学理论,从电子和空穴微观角度,并结合器件微观内特性和宏观外特性,针对晶闸管反向恢复的物理过程开展相关研究工作.

1 晶闸管二维物理模型
1.1 晶闸管仿真基本方程和模型
为了描述大功率半导体器件的内部载流子特性,通常需要求解半导体基本方程分析半导体器件在特定偏压下的各种电学特性,描述半导体器件内部载流子运输的基本方程,包括泊松方程、载流子输运方程、载流子连续性方程和全电流方程[13].为了准确描述半导体内部载流子特性,在数值计算过程中,还需要考虑载流子的迁移、碰撞电离效应、禁带变窄效应以及能量平衡等物理模型[14-15],具体表述如下:
1) 迁移率模型
本文采用平行电场依赖模型来描述高电场下的迁移率效应.在高电场作用下,电子迁移率μn(E)和空穴迁移率μp(E)的表达式为
(1)
(2)
式中:E为电场强度;μn0和μp0分别为低电场下电子和空穴的迁移率;βn和βp为两个与温度T相关的常数;Vsat为电压值.
2) 载流子生成模型
在不同电场强度下,碰撞电离率一般为电子电离率αn和空穴电离率αp的线性组合,本文采用Selberrherr模型来描述载流子的生成过程,其电子电离率αn和空穴电离率αp分别为
(3)
(4)
式中,Ani、Bni、Api、Bpi为给定参数(i=1或2).
3) 载流子统计模型
本文采用能带变窄模型来描述半导体中载流子行为的统计特征.考虑到掺杂对能带宽度的影响,即能带变窄效应,因此有效本征载流子浓度表达式为
(5)
能带变化量表达式为
(6)
式中:n0为原始浓度;k为玻尔兹曼常数;M为载流子数量.
4) 能量平衡模型
本文从Boltzmann传输方程出发,推导了能量传输方程.考虑了载流子温度的电子漂移扩散方程为
(7)
考虑了载流子温度的空穴漂移扩散方程为
(8)
式中:Tn、Tp为电子和空穴的温度;N和P0分别为电子和空穴的电子浓度;q为电子电量;Dn和Dp分别为电子和空穴的扩散系数;ψ为准费米势.
1.2 晶闸管结构模型
晶闸管PNPN内部结构及网格示意图如图1所示.设定器件内部基本物理参数如下:N-基区采用均匀掺杂,浓度为7×1013cm-3;其余区域通过扩散形成,掺杂采用高斯分布.为了使晶闸管在正反两个方向均有较高的阻断电压,设计PN结J1和J3为高浓度梯度的缓变结,P+基区表面掺杂浓度为5×1017cm-3,P基区表面掺杂浓度为3×1016cm-3;P+阳极区表面掺杂浓度为5×1019cm-3,P阳极区表面掺杂浓度为3×1016cm-3;N+阴极区表面掺杂浓度为1.5×1020cm-3.结合晶闸管PNPN结构,以晶闸管径向和轴向建立二维结构模型,其中x轴正向为晶闸管径向,y轴正向为晶闸管轴向.本文以额定电压1.8 kV,额定电流500 A的晶闸管为例,构建的晶闸管网格结构如图1b所示,其中轴向高为0.4 mm,径向宽为16.0 mm.

图1 晶闸管内部结构及网格示意图Fig.1 Schematic diagram of internal structure and network of thyristor
为了兼顾该模型数值计算的速度和准确性,设定掺杂浓度梯度较大的区域网格更为密集,因此PN结J1和J2处网格较密集,N-基区中部网格较宽.
1.3 边界条件和初始条件
如果两种类型的掺杂原子在半导体里同时存在,而且它们完全电离,则电子和空穴浓度取决于电荷中和效果.数值模拟时,假定晶闸管阳极、阴极和门极均为理想的欧姆接触,并假定初始电压均为零.当边界物理条件为欧姆接触时,表面电势、电子浓度N和空穴浓度P均为固定值,载流子准费米势与电极电压偏置相等,同时满足电中性条件.对于热边界条件,假设衬底与温度为300 K的理想热沉相连,且载流子温度相等.
在确定了物理参数模型以后,结合初始条件和边界条件,对半导体基本方程采用组合迭代(Newton迭代、Gumml迭代和Block迭代)进行数值求解,得到特定偏置下的电热参数.
2 晶闸管模型验证
利用晶闸管二维物理模型,仿真研究其直流特性,验证该模型的电压阻断特性.在SILVACO软件中,设定阳极电压分别从正、反向逐步增加至2 kV.此过程SILVACO会自动进行数值模拟,得到泄漏电流随阳极电压的变化曲线如图2所示.一般而言,当电压增幅较小时,如果泄漏电流迅速增高两个数量级,那么可以断定该电压为击穿电压.从图2中可以看出,当晶闸管两端施加的正、反向电压达到约1.8 kV时,正反向电流均迅速增大,直至击穿.由此可断定,该二维物理模型的击穿电压与器件标称额定参数基本相符,模型有效.
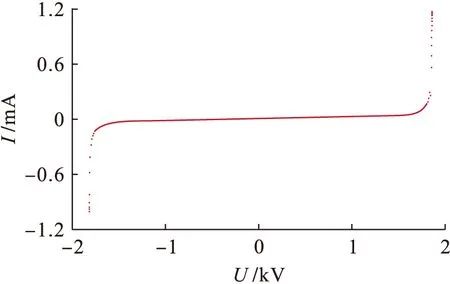
图2 晶闸管泄漏电流随阳极电压的变化曲线Fig.2 Leakage current of thristor varying with anode voltage

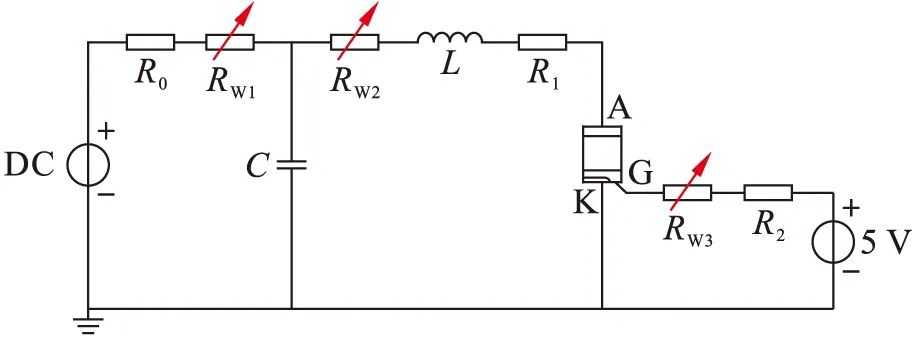
图3 工频电流下晶闸管反向恢复特性的器件电路混合模型

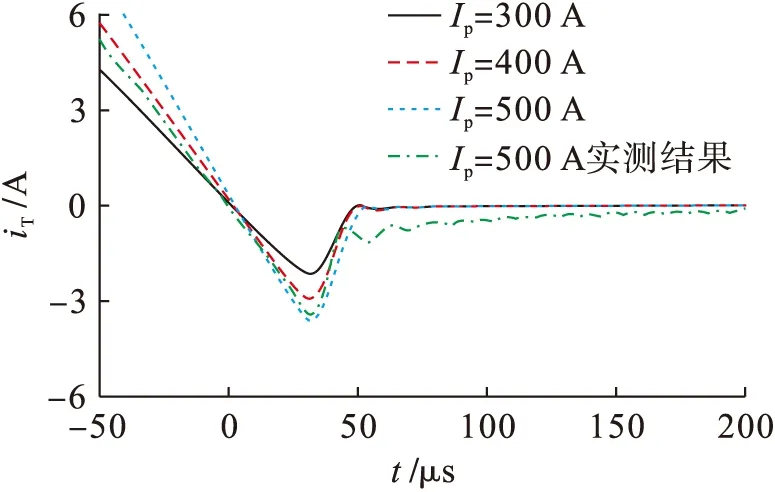
图4 不同正弦电流下晶闸管反向恢复电流仿真波形Fig.4 Simulation waveforms of reverse recovery current of thyristor under different sinusoidal currents
3 载流子消散规律

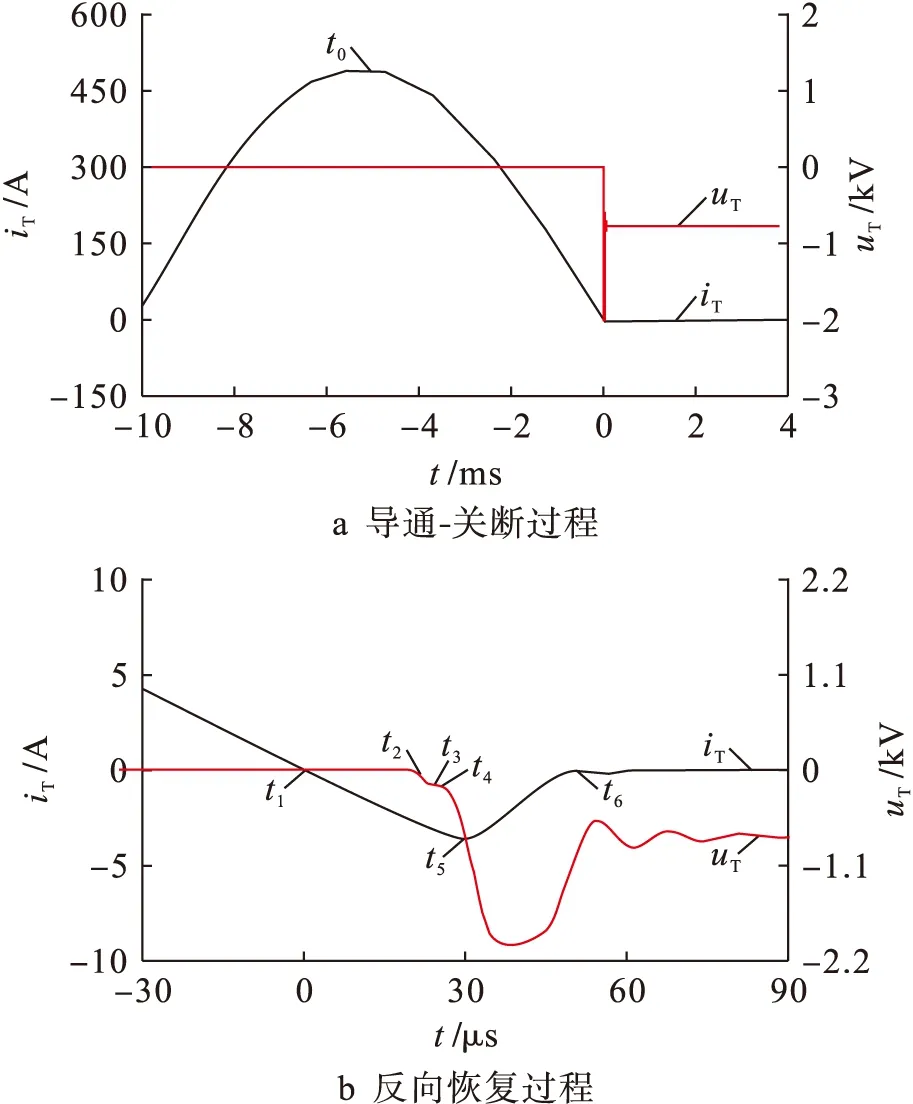
图5 工频电流下晶闸管电流和电压仿真波形Fig.5 Simulation waveforms of current and voltage of thyristor under power frequency current
如图5b所示,本文将反向恢复过程分为以下3个阶段:第1阶段为t1 第1阶段载流子浓度分布如图6所示.在t0时刻,N基区电子和空穴的浓度均约为7.9×1016cm-3,比N基区掺杂浓度7×1013cm-3高出3个数量级,属于大输入情况.由于P基极比N基极掺杂更严重,且N发射极的初始载流子浓度比P发射极低,因此对比结J3的电子浓度与结J1的空穴浓度,前者的衰减速度比后者快得多,故结J3处的非平衡载流子较结J1处率先被移除. 图6 晶闸管反向恢复第1阶段载流子浓度分布Fig.6 Carrier concentration distribution in first stage of reverse recovery process of thyristor 第2阶段载流子浓度分布如图7所示.在反向电场的作用下,随着反向恢复时间的增加,耗尽层开始扩展,结J1处的载流子浓度开始下降.根据基尔霍夫定律,电感与电阻R1两端的电压和晶闸管电压UAK之和等于反向电压Ur,电压UAK不断上升,导致反向恢复电流变化率进一步减小. 图7 晶闸管反向恢复第2阶段载流子浓度分布Fig.7 Carrier concentration distribution in second stage of reverse recovery process of thyristor 第3阶段载流子浓度分布如图8所示.从t5时刻开始,基区载流子浓度继续下降.同时,晶闸管开始恢复反向电压阻断能力.由于载流子不能被反向恢复电流扫出,导致耗尽层无法进一步扩展,剩余的非平衡载流子只能靠内部复合消失.与电流换向时刻相比,此时电子和空穴的浓度均下降了约1~2个数量级.待反向恢复电流完全衰减之后,晶闸管重新获得电压阻断能力. 图8 晶闸管反向恢复第3阶段载流子浓度分布Fig.8 Carrier concentration distribution in third stage of reverse recovery process of thyristor 第1阶段晶闸管内部载流子复合率分布如图9所示.在大注入条件下,晶闸管基区载流子浓度非常高,俄歇复合不能忽略.在工频电流导通阶段,SRH复合率与俄歇复合率接近.随着电流减小,基区载流子浓度减少,SRH复合率和俄歇复合率迅速减少. 图9 晶闸管反向恢复第1阶段载流子复合率分布Fig.9 Carrier recombination rate distribution in first stage of reverse recovery process of thyristor 第2阶段载流子复合率分布如图10所示.随着反向恢复时间的增加,SRH复合和俄歇复合反而减少,其中P基区载流子复合率变化较小,N基区载流子复合率发生明显改变.SRH复合率比俄歇复合率高4~5个数量级,因此基区内部SRH复合占主导地位. 第3阶段载流子复合率分布如图11所示.SRH复合与俄歇复合都随着反向恢复电流的衰减而减小.由于P基区掺杂浓度更高,因此P基区SRH复合率与俄歇复合率均高于N基区.同时SRH复合率比俄歇复合率高5个数量级,可见SRH复合仍然占主导地位. 图10 晶闸管反向恢复第2阶段载流子复合率分布Fig.10 Carrier recombination rate distribution in second stage of reverse recovery process of thyristor 图11 晶闸管反向恢复第3阶段载流子复合率分布Fig.11 Carrier recombination rate distribution in third stage of reverse recovery process of thyristor 针对大功率晶闸管反向恢复物理过程,采用混合模型仿真研究了工频电流导通情况下晶闸管内部载流子浓度分布及消散规律,从过剩载流子移除的微观角度阐释了晶闸管反向恢复过程的内在机理,得到了如下结论:对于工频电流下晶闸管反向恢复过程,正向工频电流存在5 ms衰减过程,从工频电流峰值至阳极电流换向阶段,基区载流子浓度衰减了近1个数量级;在工频电流正向衰减阶段,基区俄歇复合率接近SRH复合率;从阳极电流换向到反向恢复电流衰减至零阶段,载流子浓度下降了约1~2个数量级;在反向恢复过程中,SRH复合占主导地位.3.1 载流子浓度分布规律
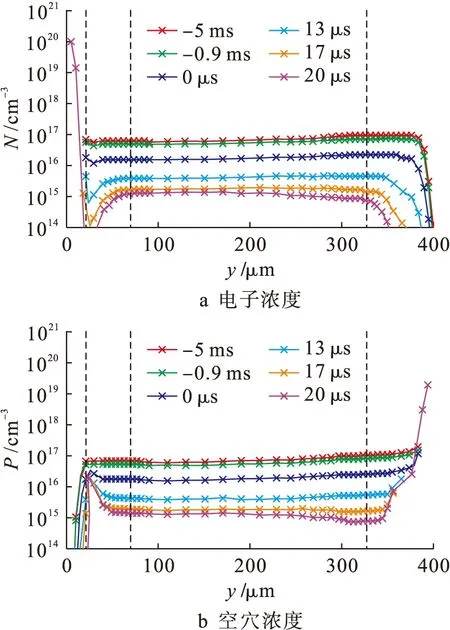

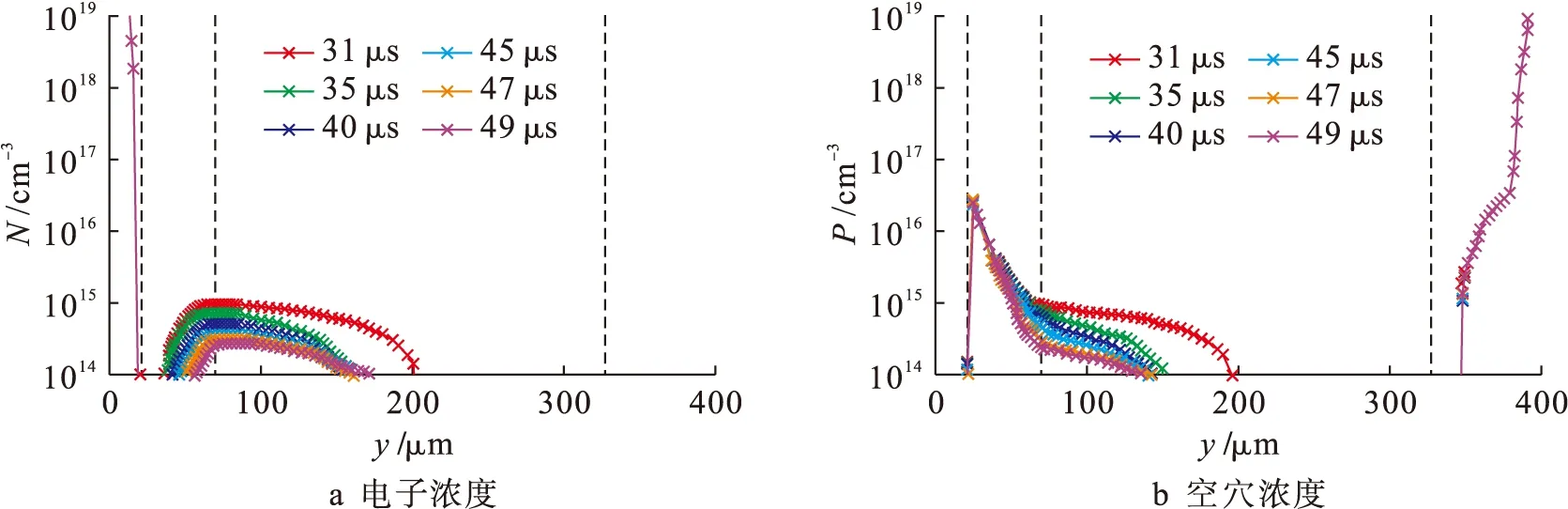
3.2 载流子复合率分布规律
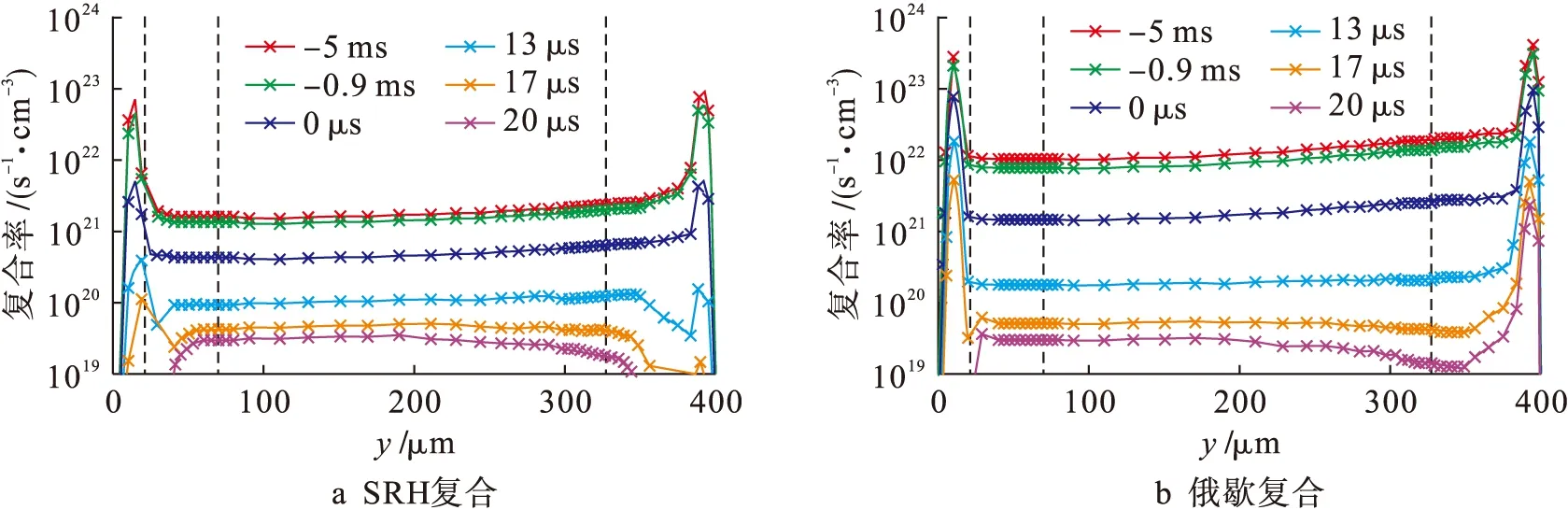
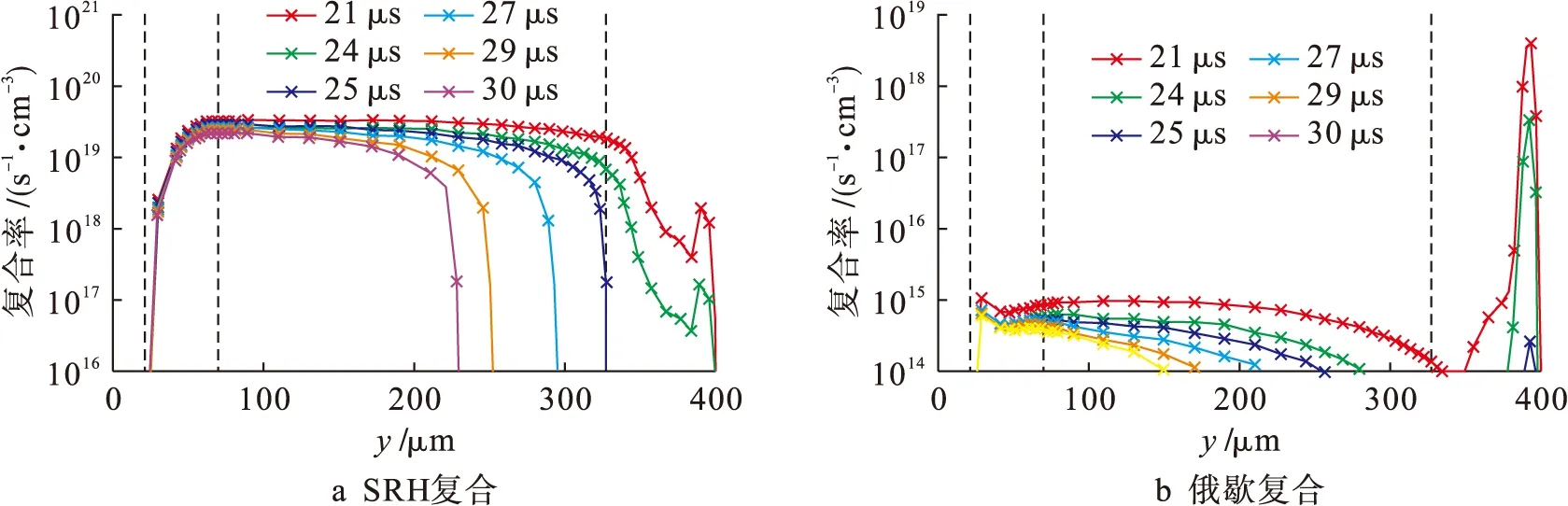

4 结 论
