改进GA-BP算法的棒式绝缘子表面缺陷识别

顾桂梅，陈国翠

(1. 兰州交通大学自动化与电气工程学院，甘肃 兰州 730070；2. 甘肃省人工智能与图形图像处理工程研究中心，甘肃 兰州 730070)

在铁路接触网中，绝缘子是保持带电物体与支柱设备或其他接地体之间电绝缘的重要部件，若绝缘子发生破损、自爆，轻则会损坏接触网设备，重则将会导致列车的骤停甚至造成人员伤亡，而缺陷识别的前提是准确识别出绝缘子。近年来，基于图像处理的非接触式识别技术可在列车安全运行而不被干扰的条件下实现相关操作。在4C中，绝缘子图像检测与成像分析装置大多采用人工逐帧判别[1]的方式实现风险识别，存在识别工作量大、耗时长、实时性差等问题。为此，许多国内外相关学者对其识别技术及分析方法进行了相关研究。邓斌等[2]指出绝缘子三维位置重建方法的不足，即接触网绝缘子和支架的距离存在一定的范围限制(1 200～3 200 mm)。李彩林等[3−4]采用深度学习算法实现了绝缘子的精确定向识别，但不稳定性还需进行相应的改善。DHAR 等[5]提取绝缘子特征并作为支持向量机的输入，实现绝缘子缺陷的识别，其人工参与量较大。张友鹏等[6]等利用GA-BP 算法来提高绝缘子泄漏电流预测的准确率，但此种方法并未在绝缘子识别问题上进行验证。基于此，本文针对棒式绝缘子及其缺陷识别准确率较低的问题，采用改进GA-BP 算法和水平/垂直方向像素统计的算法。首先将GA 和BP 算法结合，对网络的初始权值、阈值进行优化；然后，通过鲍威尔-比厄法不断更新GA-BP 算法中的权值和阈值，改进其收敛速度，最终实现绝缘子高精度识别；最后，针对绝缘子表面缺陷识别种类单一问题，利用相机标定和绝缘子水平/垂直方向像素统计结果，实现绝缘子破损、自爆状态识别并提高缺陷识别的准确度。

1 改进GA-BP绝缘子识别算法

BP 网络[7]是一种局部搜索的多层前馈神经网络，最速下降法会在目标函数快要接近极小点时，产生因锯齿现象使收敛速度发展变慢的不足。遗传算法[8]是一种全局搜索的能够模拟自然物种进化过程并寻找最优解的方法。故本文利用Powell-Beale 的优势即二次终止性、收敛速度较快及迭代结束后搜索梯度方向还原为负梯度反向，将其作为BP 算法的学习规则，克服易收敛到最小局部问题。

本文3 层网络中输入层的节点数M=32，输出层的节点数Q=40，隐含层节点数N=2M+1=65[9]。设绝缘子图像Xi(i=1,2,…,m)为输入样本，具体识别步骤如下。

步骤1：读入绝缘子图像并转换成灰度矩阵，然后将灰度矩阵进行分割并对每个分割后的小矩阵进行奇异值分解(Singular Value Decomposition,SVD)降维，提取32 维特征值，编码初始群体。设Xi×j为网络初始权值，每个基因值是一个连接权值，则当前个体长度L为：

式中：M代表输入层节点数；Xi代表第i个个体基因；Xi(p)代表第i个个体的第p个基因；q代表第p+1个基因值对应的阈值宽度。

步骤2：采用GA 对BP网络的初始权值进行优化，计算个体的适应度均值，确定是否是迭代的最大数。适应度函数定义如下：

其中，e为测试绝缘子样本输出误差值。进化代数即平均适应度曲线如图1所示。

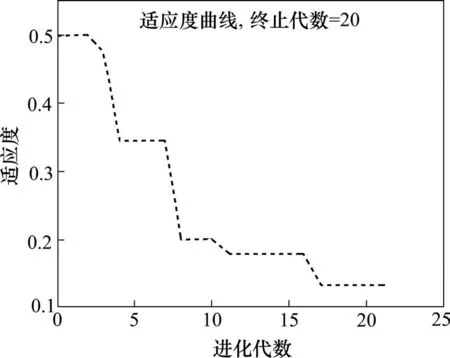
图1 平均适应度曲线Fig.1 Mean fitness curve

图2中，平均适应度曲线呈梯度型下降，当种群进化代数大约等于17 时，其平均适应度达到稳定值(0.1～0.15)，故本文取进化代数为20。

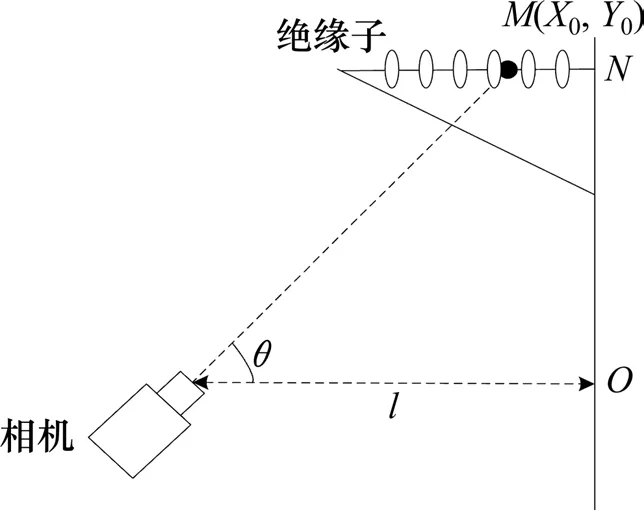
图2 转换模型Fig.2 Transformation model diagram

步骤3：确定收敛条件是否满足(1×10-5)，若满足，则进入BP 网络操作,采用Powell-Beale 法构造搜索方向并计算网络系统最优权值和阈值。迭代结束后网络搜索梯度方向d(k)还原为负梯度反向；ν表示一个隐含层的输出；wmn和wnq分别为输入层到隐含层和隐含层到输出层的权重矩阵，BP 神经网络隐含层的阈值为a=[a1,a2,…,an]，输出层的阈值为b=[b1,b2,…,bq]。隐含层、输出层输出为：

其中：k代表迭代次数；λ(0≤λ<1)是鲍威尔-比厄因子；η(η>0)为学习速率，大小由式(11)决定。

其中，wnq(k)为第k次循环时的网络隐含层权值输出；yk是网络的期望输出；ok是实际输出。

步骤4：判断识别的结果是否满足终止条件(yk-ok=0.01)，若满足则输出结果，否则转步骤3。

2 绝缘子表面缺陷识别

2.1 张正友标定法

张正友标定法是张正友于1998 年提出的一种棋盘格的相机标定方法，是目前使用最广的一种相机标定方法。本文相机标定得到的内外参数如表1所示。

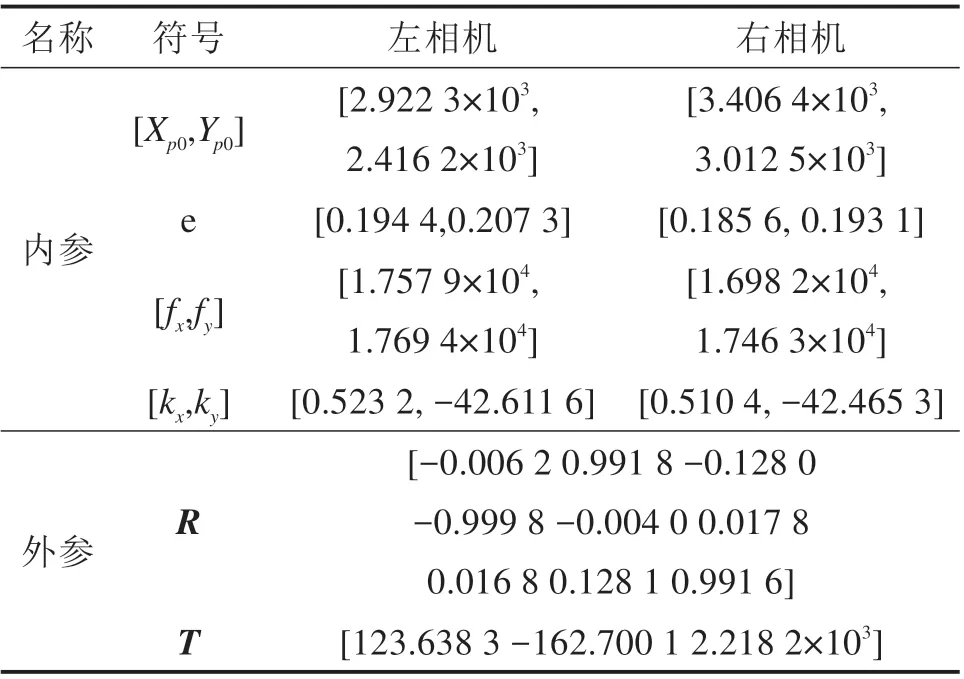
表1 相机的内外参数Table 1 Internal and external parameters of the camera

2.2 最小二乘法拟合绝缘子直线

最小二乘法拟合算法[10]对绝缘子图像进行直线拟合，寻找与目标绝缘子第一片伞裙相垂直的直线L′，交点即伞裙质心d(xm,ym)，m=1,2,…11。设绝缘子图像中心线方程为L:y=ax+b，直线L′的表达式为y=a′x+b′。针对破损绝缘子，拟合直线步骤如下。

其拟合直线L结果为y=0.387 3x+20.837 3。

步骤4：计算与L垂直的直线L′:y=a′x+b′。

由tanα=0.387 32，则α=arctan(0.387 3)，故tanβ=a′。根据三角形关系，得β=α+ 90°，即a′ = -2.582 0。并将点(x1,y1)代入直线L′，得b′=140.6112，故直线L′的表达式为y′= -2.582 0x+140.6112。

2.3 基于像素统计的绝缘子表面缺陷识别

结合相机标定和绝缘子像素统计结果，实现绝缘子表面缺陷识别。具体实现步骤如下。

步骤1：相机标定，实现世界与像素坐标系下绝缘子长度直径比的转换，其转换模型如图1所示。

图2中，l为相机与钢柱间的距离(l=2 000 mm)；ON为相机与目标绝缘子间的垂直距离；θ为相机与水平方向的夹角(本文中θ=80°)，其大小根据拍摄目标范围和高度的不同而改变；M(X0,Y0)为摄像头光心在绝缘子表面对应的点。利用小孔成像原理，可得绝缘子图像上的点(x,y)的横坐标x和世界绝缘子表面上的点(X,Y)中X间的关系为(Y同理)：

其中：X1，X2分别为世界坐标系中绝缘子平面左右端点的横坐标；x1，x2分别为图像坐标系中绝缘子图像相对应左右端点的横坐标像素值；H和D分别为绝缘子的物理长度和直径；h'，d'分别为正常绝缘子像素和平均直径；kx，ky为径向畸变参数；px，py为切向畸变参数(所占比重不大，接近于0，在要求极其精确时才考虑此参数)；xk，yk为畸变量。

步骤2：输入绝缘子灰度图，利用plt.gca().yaxis/xaxis 统计绝缘子图像的垂直/水平方向的像素。

步骤3：调用库中cv2.threshold 函数，实现绝缘子灰度图像的二值化转换。

步骤4：利用height=th3.shape，width=th3.shape计算绝缘子的长和宽，进而计算其长度直径比rs。若绝缘子存在自爆，则rs＞r'(r'为对应正常绝缘子的像素长度直径比)，否则就为正常或破损绝缘子。

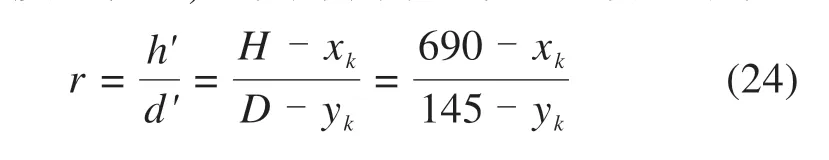
步骤5：将直线L′依次向右移Lave(绝缘子伞裙与伞裙距离)个单位，采用area=Column WhiteTo‐talNum语句计算绝缘子伞裙面积as。

步骤6：L′依次向右移Lave个单位，直至伞裙面积统计结束并显示结果，绝缘子缺陷识别结束。本文算法流程如图3所示。

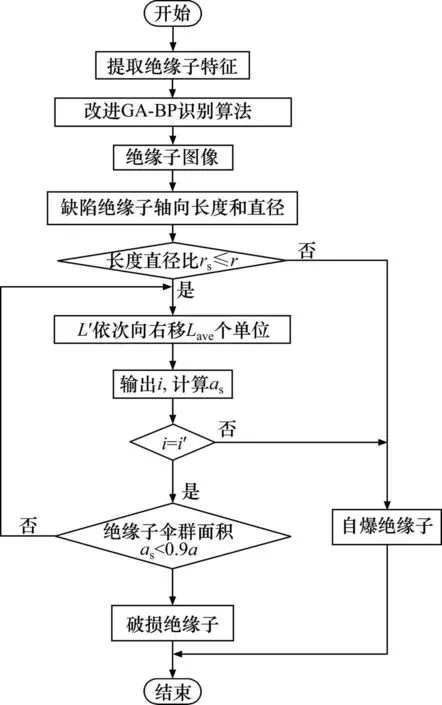
图3 算法流程Fig.3 Flowchart of algorithm

3 仿真验证与分析

以Opencv 为平台，硬件配置为Intel(R) Core CPU，仿真主机为主频1.80 GHz，内存8.00 GB，双显卡的计算机。以棒式绝缘子图像作为验证数据，随机选取400 幅只包含绝缘子的图像(120×90)，其中，240 幅图像作为训练集，160 幅图像作为测试集。将绝缘子32 维特征作为输入实现绝缘子精确识别，本文改进算法的测试样本输出误差拟合曲线(期望与输出间的差值(yk−ok=0.01))如图4所示，即所用时间为6.057 7 s。网络训练的误差收敛曲线如图5 所示，绝缘子识别的准确率如表2所示。

图4 输出误差拟合曲线Fig.4 Output error fitting curve

图4中，本文算法预测输出值与期望值之间的差值接近于0.01，具有较好的拟合精度。图5 中，箭头①所指虚线为网络的预设训练目标(1×10−5)，箭头②所指虚线为网络的实际最优训练评估值(0.01)，实线为网络的训练收敛速度。BP算法和文献[11](GA-BP 算法)训练至1 000 次、987 次的最优训练评估值分别为0.010和0.024，而本文识别算法在训练至803次便已达到最优训练评估值，评估值为0.013。BP 算法和文献[11]在网络分别训练的前400次、200次(圆圈，下同)，收敛速度曲线便下滑至接近训练目标值；而本文方法在网络训练的前100 次，收敛速度曲线便已迅速下滑至接近训练目标值，证明本文方法对网络训练的收敛速度有显著提升。表2 为3 种绝缘子识别算法的识别结果，BP 算法、文献[11]算法的绝缘子总识别率分别为75.0% 和88.5%，本文改进算法的总识别率为95.5%。故本文算法不仅提升了神经网络的收敛速度，而且识别率也得到了有效提高。

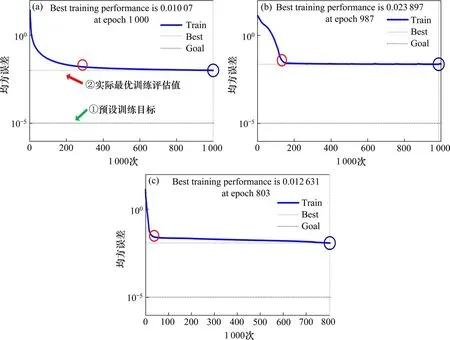
图5 不同算法网络训练收敛曲线结果对比Fig.5 Comparison graph of convergence results of network training of different algorithms

表2 绝缘子识别准确率结果Table 2 Results of insulator recognition accuracy

针对本文所列的破损、自爆绝缘子的垂直/水平方向像素统计结果如图6所示，其长度直径比和伞裙面积计算结果如表3所示。

图6 中，其Lave为7pixel(Lave为避免误差而删除最大和最小距离后的均值)，由垂直、水平方向的像素统计结果可计算出绝缘子的长度和半径。表3中，破损、自爆绝缘子的像素长度直径比为3.944和3.318；伞裙面积的平均值分别为242 和362，破损绝缘子伞裙结果显示共有11 片，且第10 和11 片伞裙面积出现异常(216/253)，其第10 片伞裙明显过小而第11 片明显过大，说明其绝缘子第10 片出现了破损。因工业CCD 相机的拍摄角度，使得第11 片绝缘子伞裙与其环孔无明显过度灰度界限，使得该绝缘子伞裙面积明显过大(253)，但第10 片绝缘子伞裙的面积并无异常(216)，因此，第11 片绝缘子伞裙并无缺陷；对于自爆绝缘子，只计算出了10 片伞裙的面积，且其第5 片伞裙明显过大(639)而第6 片伞裙面积并无减小(345)，说明其绝缘子第5 片出现了自爆缺陷。因工业CCD 相机拍摄的角度，使得第10 片绝缘子伞裙与其环孔无明显过度灰度界限，第10 片绝缘子伞裙面积明显过大(601)，但第9 片绝缘子伞裙的面积并无异常(335)，因此，第10 片绝缘子伞裙并无缺陷。其绝缘子缺陷识别结果如图7 所示，准确度对比如表4所示。

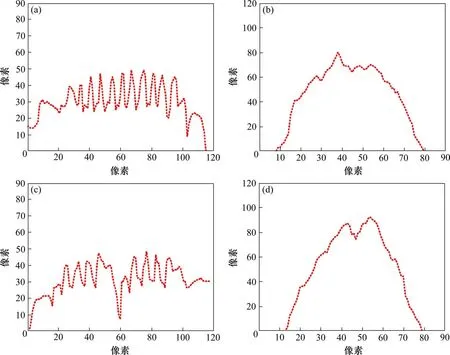
图6 绝缘子垂直/水平方向像素统计Fig.6 Statistic image of insulator pixels in vertical/horizontal direction

图7 绝缘子缺陷识别结果Fig.7 Insulator defect identification results

表3 绝缘子长度直径比及伞裙面积计算结果Table 3 Calculated results of insulator length-diameter ratio and umbrella skirt area

表4 中，文献[12]利用绝缘子图像垂直方向的像素统计，计算伞裙间的距离Li，以Li>1.6Lave为百度按标准，若满足上式，则第i+1片绝缘子伞裙发生了自曝，其自爆缺陷识别精度较低(72.50%)，且只可识别出自爆绝缘子。本文则在此基础上，将绝缘子的长度直径比和绝缘子伞裙面积作为自爆、破损的判断依据，具有较高的精确度(93.00%)且可同时识别出自爆和破损绝缘子。

表4 绝缘子识别准确率结果Table 4 Insulator identification accuracy results

4 结论

1) 针对高速铁路接触网棒式绝缘子的准确识别问题，将BP 网络的局部搜索、收敛速度慢与GA 算法的全局搜索结合，利用Powell-Beale 因子构造GA-BP 算法的搜索方向，在提升收敛速度的同时，绝缘子识别准确率也得到了提高。实验仿真结果表明，相比BP 算法和GA-BP 算法，本文改进GA-BP 算法对绝缘子识别率分别提高了20.50%和7.00%，且平均每张绝缘子图像的处理时间为0.015 s。

2) 对于绝缘子表面缺陷识别类型单一问题，利用相机标定实现绝缘子坐标转换，然后统计绝缘子像素并计算绝缘子长度直径比，最终将绝缘子长度直径比和伞裙面积作为绝缘子破损、自爆缺陷的判断标准，实现绝缘子状态的识别并进行缺陷标记，识别精度为93.00%。相比于单纯依靠绝缘子伞裙距离作为自爆识别标准，本文算法的识别精度提高了20.50%。这对4C 在目标识别中的工作量大、耗时长、实时性差等问题的改善提供了理论依据，对实际工程具有一定的参考意义。