接触网周围流体流动及传热特性的数值模拟

杨晓彬，林国松,2，李原，张硕，潘飞

(1. 西南交通大学电气工程学院，四川 成都 611756；2. 西南交通大学国家轨道交通电气化与自动化工程技术研究中心，四川 成都 611756)

接触网作为电气化铁路牵引供电系统的重要组成部分，承担着将从牵引变电所获得的电能供给电力机车的重要任务，其运行性能和工作状态是否良好直接影响着弓网系统的受流质量，进而关系到铁路运输的安全性和可靠性。接触网常年裸露于空气中，大风、悬挂结构覆冰等随机环境荷载都会造成接触线偏移或振动，严重时甚至会出现大幅舞动现象，导致线索、金具磨损严重，使用寿命缩短[1]。因此，研究接触网导线的气动参数具有重要意义。另外，随着高寒、高海拔电气化铁路投入运营，因地形、气候等环境因素影响，接触网覆冰现象频发，在线防冰技术应运而生，其技术核心之一是根据接触线表面的热平衡方程来确定防冰电流[2-3]。但高速铁路接触线的截面形状非标准圆形，而是两侧带有悬吊沟槽的规则圆形，其传热特性与圆形导线不同，这就需要研究分析不同雷诺数下接触线表面的传热参数。目前，对于气动参数的研究，主要有风洞试验和数值模拟2 种方法。谢强等[4]采用风洞试验方法，测量了不同湍流强度下AC-150 型接触线的气动参数。然而，风洞试验存在费用高、周期长、测量精度有限以及试验模型和实际问题的等效性难以确定等缺点[5]。因此，众多学者通过计算流体力学软件数值计算了多种不同情况下导线的气动参数。张友鹏等[6]通过建立正馈线的外流场模型，研究了大风区段挡风墙对正馈线气动特性的影响；宋洋[7]基于CFD 仿真模型计算了不同磨损程度接触线的气动参数，进而确定了接触网舞动的发生区域；汪宏睿等[8]则利用CFD 软件(Fluent)模拟了接触线周围的空气流场，并研究了不同迎风攻角、不同风速下接触线气动参数的变化规律。但上述文献均未系统地分析不同雷诺数下承力索和接触线气动参数的差异，且流动模型的模拟精度有待考量。对于导线传热参数的研究，多以电力系统中的架空输电线为主，而与接触线相关的研究则集中在接触线温度场方面。MATTERA 等[9]通过建立接触线的二维径向热路网络，对因径向温度梯度过高导致的机械故障进行了热分析；郭凤仪等[10]则利用COMSOL 软件研究了电弧位置和电弧能量对弓网系统接触线温度的影响。因此，为探究不同雷诺数下接触网导线的气动参数和传热参数，本文以承力索和接触线为研究对象，通过建立接触网导线的流体-热耦合数值模型，分别对承力索和接触线的流场和温度场进行数值模拟，并将数值模拟结果与SSTk-ω模型以及公开的实验数据进行比较，以分析不同流动模型的模拟精度。

1 流体−热耦合数值模型

在流体力学中，任何流动问题都必须遵循3个基本的物理学原理：质量守恒定律、牛顿第二定律和能量守恒定律。因此，首先，基于流体流动的基本控制方程给出流体-热耦合模型的数学描述；然后，针对接触网导线绕流确定流动模型；最后，给定其物理模型和参数定义。

1.1 模型的数学描述

由于本文研究的流体为空气，流场中流体的流速范围为0.001～30 m/s，且接触网导线与流体的温差不大，故为简化分析，做出如下假设：

1)流体为不可压缩牛顿流体；

2)流体的物性参数为常数且无内热源；

3) 流体的体积力、体积加热、黏性耗散热可忽略不计。

在上述假设的基础上，结合气体的状态方程，流体-热耦合模型可描述为如下形式：

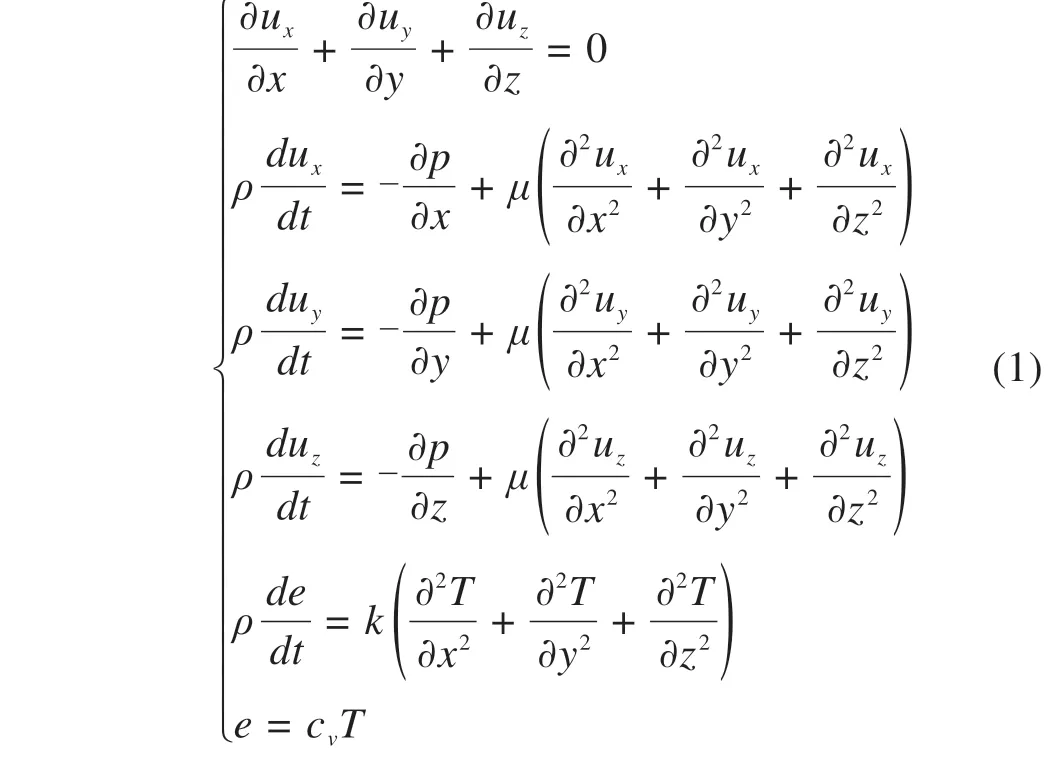
式中：ux，uy，uz分别表示坐标x，y，z方向上流体的速度分量；ρ，μ，k，cv分别表示流体的密度、动力黏度、导热系数和比定压热容，p，e，T，t分别表示压力、单位质量流体的内能、温度和时间。该方程组包含了10个未知量，而列举的方程仅有6个，再给定4个物性参数：ρ，μ，k，cv，便可使方程组封闭。

1.2 流动模型

接触网导线绕流的数值模拟，本质上是钝体绕流问题，而圆柱绕流作为钝体绕流中的典型代表，直到现在仍是CFD 领域的一大研究热点。对于低雷诺数流动，文献[11]使用二维非定常层流求解器数值求解了40≤Re≤140内圆柱的强制对流换热特性，且模拟结果与试验结果非常吻合。对于高雷诺数流动，CFD 软件中引入了2 类湍流模拟方法：雷诺平均模拟方法(Reynolds Averaged Navier-Stokes Simulation, RANS)和大涡模拟方法(Large Eddy Simulation, LES)。目前，Fluent 提供了多种基于RANS 的湍流模型，主要包括：单方程模型(Spalart-Allmaras 模型)、双方程模型(k-ε模型、k-ω模型及其变种模型)及雷诺应力模型等，但文献[12-13]指出，使用非稳态RANS 模拟亚临界区的圆柱绕流时，模型的适用性下降，不能准确预测边界层从层流到湍流的转变以及边界层的分离，进而导致气动参数过度预测。与RANS相比，虽然LES对计算机的内存和计算速度的要求较高，但文献[14-15]使用LES 成功地模拟了亚临界区的圆柱绕流，且其预测精度较RANS有很大提高。

基于上述描述，本文的流动模型选择层流模型和大涡模型，即低雷诺数的流动模拟采用层流模型，高雷诺数的流动模拟采用大涡模型。

1) 层流模型

在笛卡尔坐标系下，给出非定常流动层流模型的控制方程：

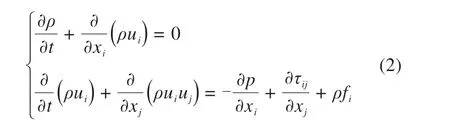
式中：i,j=x,y,z；τij表示作用在垂直于i方向的平面上沿j方向的应力；fi表示作用在单位质量流体上的体积力沿i方向的分量。

2) 大涡模型

LES 通过在Fourier 空间或物理空间对非稳态N-S 方程进行过滤，以滤除小于过滤器宽度或网格尺寸的旋涡，从而得到大涡的控制方程。以不可压流动为例，大涡模型的控制方程如下：

式中：带有上划线的变量为滤波后的场变量，σij，τij分别表示作用在垂直于i方向的平面上沿j方向的黏性应力张量和亚格子应力。

1.3 物理模型和参数定义

电气化铁路中，承力索多采用铜合金绞线，其截面近似为圆形，而接触线截面形状则为两侧带有悬吊沟槽的规则圆形。虽然它们的截面形状不同，但外流场模型具有相似的物理形式，因此，这里仅给出承力索外流场的三维物理模型，具体见图1。外流场的三维物理模型采用笛卡尔坐标系作为参考坐标系，坐标原点位于承力索截面中心处，x，y，z方向分别为顺流向、横流向和展向。以承力索直径D为特征尺寸，三维物理模型的计算域尺寸为60D×40D×πD，承力索中心距上、下游边界的距离分别为20D和40D，距侧面边界的距离都为20D，这种配置可使阻塞效应忽略不计。

图1 承力索外流场的三维物理模型Fig.1 Three-dimensional physical model of the external flow field of carrier wire

对于钝体绕流，气动参数主要包括阻力系数CD，升力系数CL以及斯特劳哈尔数St，都属于无量纲量，具体定义如下：

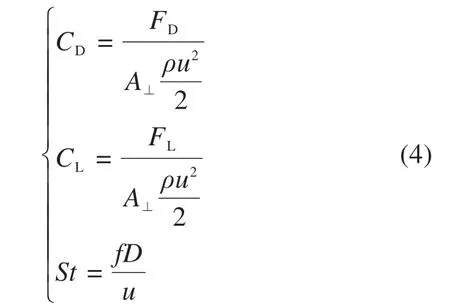
式中：FD和FL分别表示钝体受到的阻力和升力；A⊥表示钝体垂直于流向的投影面积；f表示旋涡脱落频率。

传热参数中，钝体表面与周围流体的对流换热可通过下式描述：

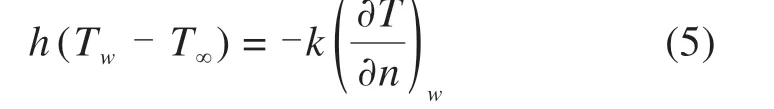
式中：h表示对流换热系数；Tw，T∞分别表示钝体壁面温度和流体温度；n表示钝体壁面的法向方向。

钝体壁面的局部努赛尔数Nuw和面积平均努赛尔数Nua可分别通过式(6)和式(7)计算。

式中：hw表示局部换热系数；A表示钝体壁面面积。

气动参数和传热参数的时均值均可通过下式表示：

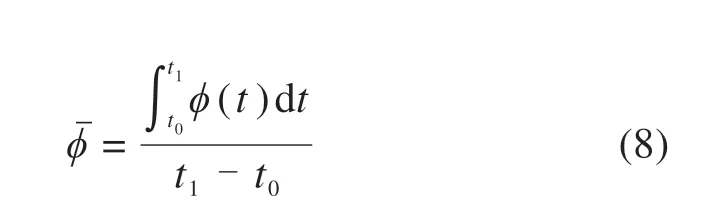
式中：t1–t0为统计时间，需至少为15 倍的涡脱周期。

2 数值模拟

目前，国内主要的高速铁路运营线路，如京沪线、哈大线均采用截面积为150 mm2的接触线和120 mm2的承力索。因此，以这2 种导线为研究对象，进行数值模拟。承力索截面近乎圆形，一般可将其视为圆柱体。接触线截面为带有悬吊沟槽的规则圆形，具体见图2。因合金种类识别沟槽和圆角的半径很小，故图2忽略了它们对接触线截面的影响。

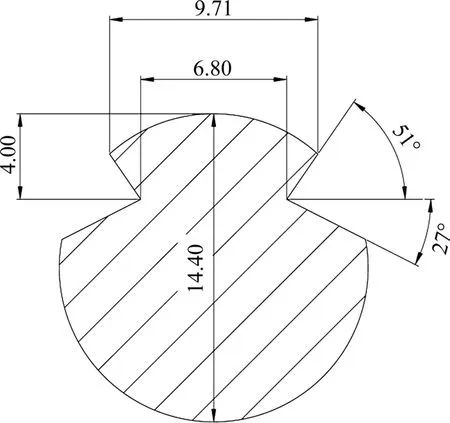
图2 接触线截面Fig.2 Cross section of contact wire

由于钝体壁面处存在速度边界层和热边界层，边界层内速度梯度和温度梯度较大，为精确求解近壁面处流场和温度场，就需要在边界层内布置较多的节点。因此，文中接触网导线外流场采用分块划分方式，近壁面采用160×30 的O 型网格，且边界层网格的设置需符合流动模型的要求，其他区域的网格则为四边形网格(二维)或六面体网格(三维)，展向方向的网格尺寸约为0.1D，具体的网格划分见图3和图4。

图3 承力索计算域网格Fig.3 Mesh of the computational domain of carrier wire

图4 接触线计算域网格Fig.4 Mesh of the computational domain of contact wire

根据1.2 节中的流动模型，给出数值模拟中不同雷诺数下流场的求解设置及流动模型，具体见表1。

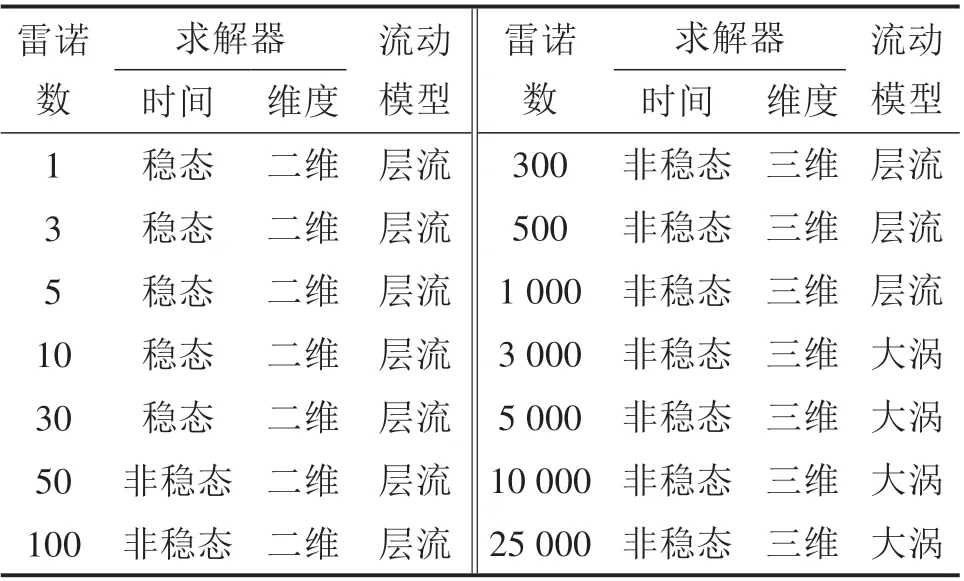
表1 不同雷诺数下流场的求解设置及流动模型Table 1 Solution setting and flow model of flow field under different Reynolds numbers

数值模拟过程中，入口设置为速度入口，来流速度u可根据不同的雷诺数计算得到，来流温度T∞=293.15 K；导线表面设置为无滑移、恒温壁面，壁面温度Tw=298.15 K；出口设置为自由流出口，上下壁面都设置为无滑移、绝热壁面，展向方向的2个对称面设置为周期面，流体的物性参数则根据表2设置。

表2 293.15 K时流体的物性参数Table 2 Physical parameters of fluid at 293.15 K

至于方程的离散和求解，稳态时，压力与速度耦合的求解采用SIMPLE方法，非稳态时，则采用PISO 方法；层流模型时，动量方程和能量方程中的对流项采用2 阶迎风格式，时间项则采用2 阶隐式推进法；大涡模型时，动量方程和能量方程中的对流项采用有界中心差分格式，时间项则采用有界2阶隐式推进法。

3 模型验证及结果分析

3.1 流动模型的验证

为验证流体-热耦合数值模型中流动模型的模拟精度，采用层流(大涡)模型、SSTk-ω模型分别对雷诺数为300，500，1 000，3 000 和5 000 时的承力索流场和温度场进行数值模拟，提取其气动参数和传热参数，并将数值模拟结果与公开的实验数据[16]进行比较，以分析各流动模型的模拟精度，具体见表3。

由表3可知，当Re≤1 000时，层流模型的模拟误差最小，最大相对误差仅为7.0%，而SSTk-ω模型的最大相对误差可达34.7%。当Re≥3 000时，大涡模型的模拟误差最小，最大相对误差仅为5.1%，而SSTk-ω模型的最大相对误差可达39.8%。因此，与SSTk-ω模型相比，低雷诺数选用层流模型、高雷诺数选用大涡模型的流体-热耦合数值模型的模拟精度更高。

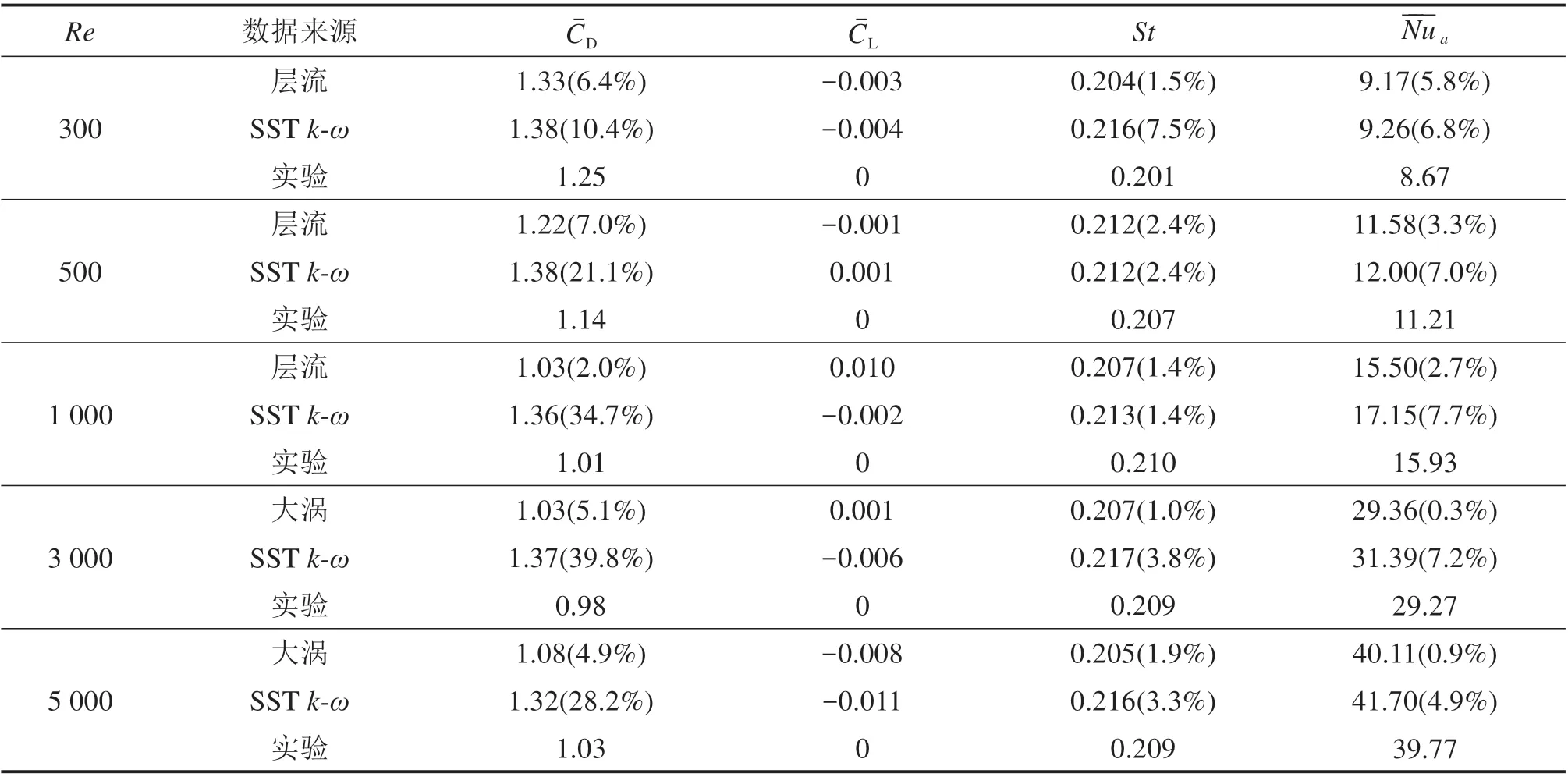
表3 数值模拟结果与实验数据的比较Table 3 Comparison of simulation results and experimental data

3.2 流场及气动参数

为探究不同雷诺数下接触网导线的气动参数，利用求解器Fluent分别对承力索和接触线的流场进行数值模拟。图5给出了几个典型雷诺数下接触网导线的流场分布。

从图5 可看出，当Re=1 时，流动为蠕动流，承力索上下表面的流场对称，而接触线的流场因沟槽丧失了对称性；当Re=30 时，流动出现分离，承力索尾流中出现一对固定且对称的旋涡，而接触线尾流中的上旋涡稍比下旋涡大；当Re=100时，尾流中都出现交替脱落的旋涡，并逐渐形成层流涡街；当Re=5 000 时，自由剪切层中都存在层流到湍流的转变，且尾流变为完全湍流。

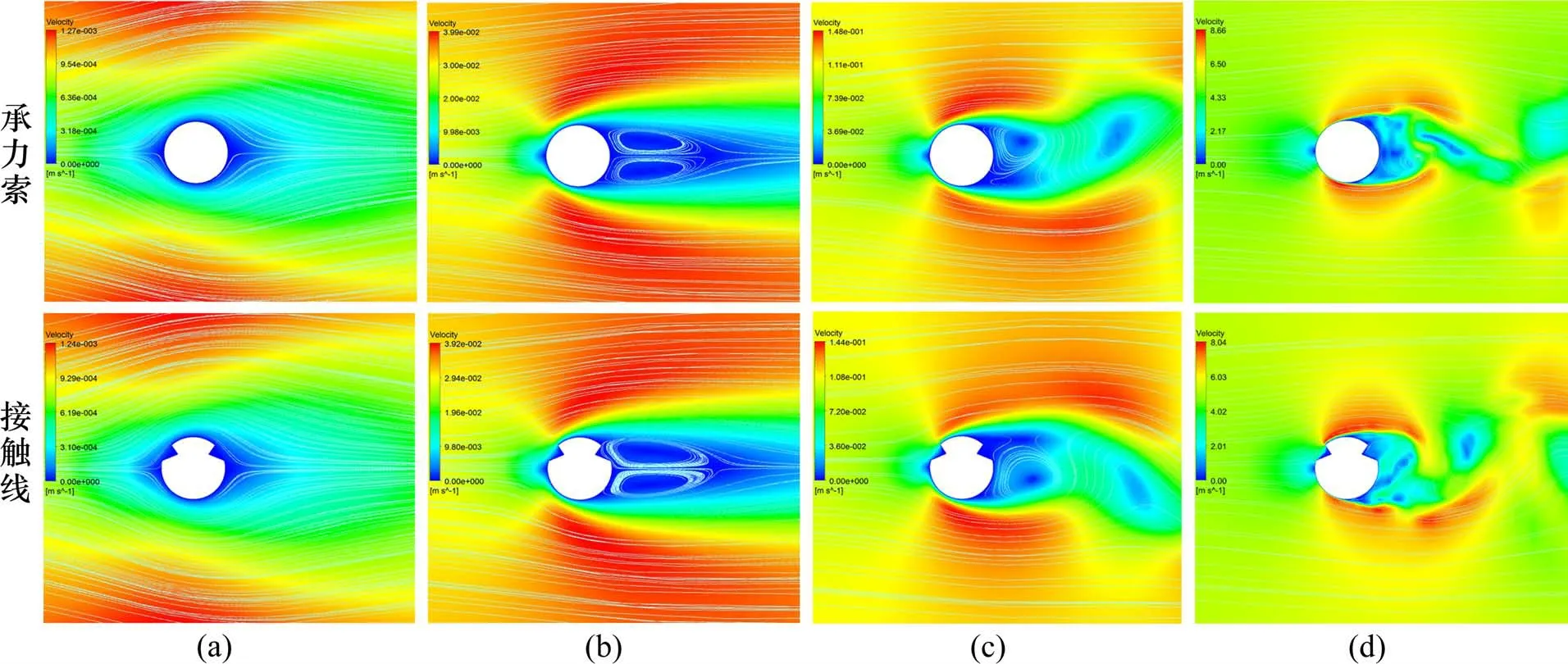
图5 接触网导线的流场分布Fig.5 Flow field distribution around catenary wires

图6则给出了接触网导线气动参数随雷诺数的变化规律。

从图6可看出，接触线由于沟槽的存在，其气动参数与承力索的气动参数存在明显的差异，主要表现在：1)当Re≥300 时，接触线的阻力系数高于承力索的阻力系数；2) 接触线的升力系数明显不同于承力索，其升力系数为负值，且当Re≥1 000 时，其升力系数出现明显的骤降；2) 当Re≥300 时，接触线的斯特劳哈尔数明显低于承力索的斯特劳哈尔数。

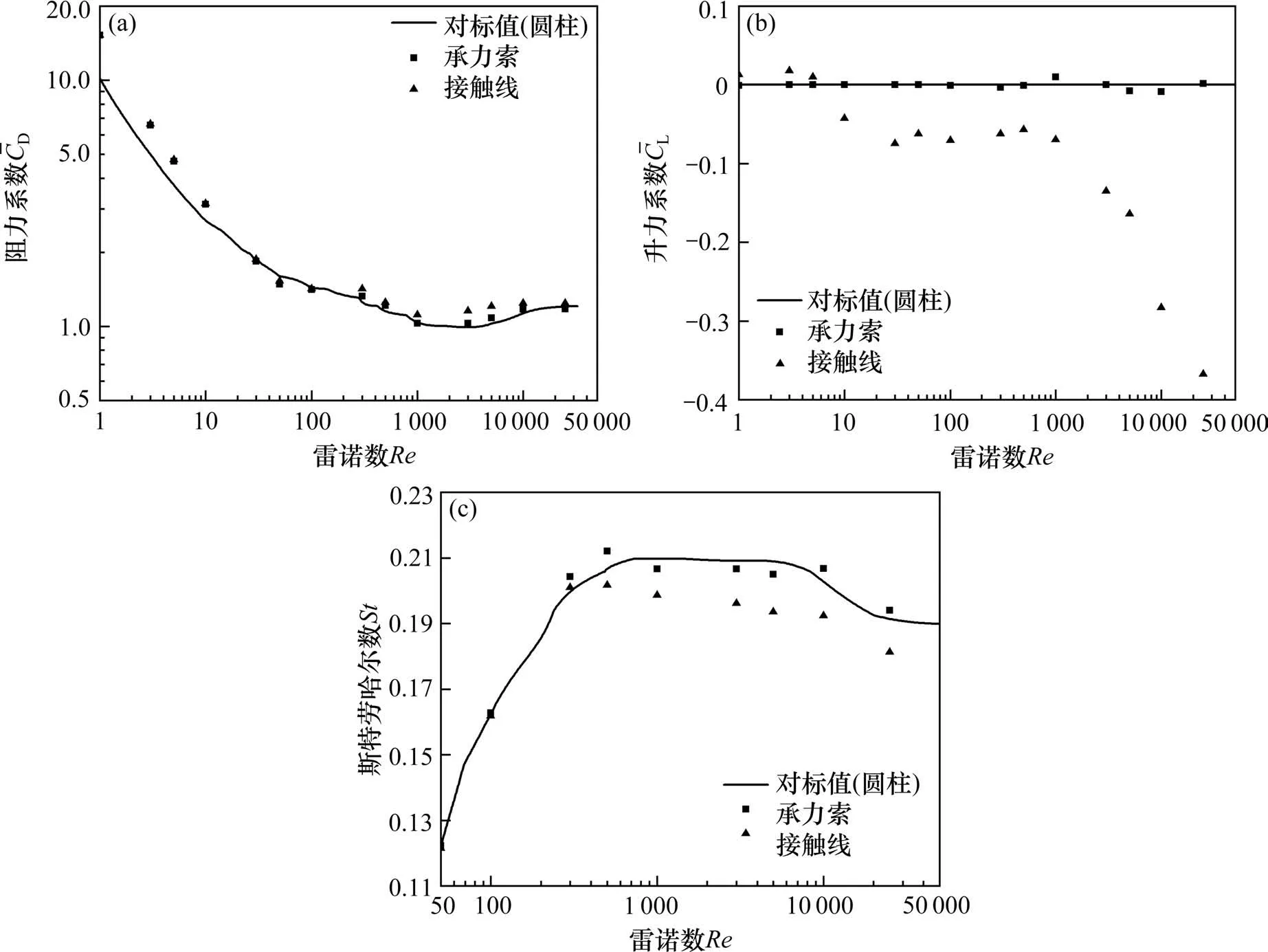
图6 不同雷诺数下接触网导线的气动参数曲线Fig.6 Curves of aerodynamic parameters of catenary wires under different Reynolds numbers

3.3 温度场及传热参数

为探究不同雷诺数下接触网导线的传热参数，利用求解器Fluent分别对承力索和接触线的温度场进行数值模拟。图7给出了几个典型雷诺数下接触网导线的温度场分布。

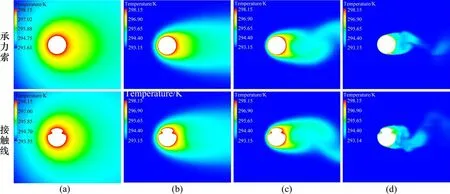
图7 接触网导线的温度场分布Fig.7 Temperature field distribution around catenary wires

从图7可看出，承力索和接触线迎风面的温度边界层厚度都比背风面的薄，且温度边界层的厚度都随雷诺数的增大而减小，这表明迎风面的换热性能要比背风面的好，且导线整体的换热性能随雷诺数的增大而增强。但接触线与承力索也存在不同之处，接触线沟槽处的温度梯度较小，这表明沟槽处的换热性能较差。

工程中，对流换热参数的计算一般是基于面积平均努赛尔数的，因此，图8给出了接触网导线面积平均努赛尔数——Nu a随雷诺数的变化规律。

图8 不同雷诺数下接触网导线的传热参数曲线Fig.8 Curve of heat transfer parameters of catenary wires under different Reynolds numbers

从图8可看出，承力索和接触线的面积平均努赛尔数都随雷诺数的增大而增大，同时，经计算发现，当Re≥50 时，接触线的——Nu a比承力索的——Nu a低9%以上，这表明接触线因沟槽的存在，其换热性能一定程度上低于承力索的换热性能。

4 结论

1)与SSTk-ω模型相比，低雷诺数选用层流模型、高雷诺数选用大涡模型的流体-热耦合数值模型的模拟精度更高，气动参数的最大相对误差仅为7.0%，传热参数的最大相对误差仅为5.8%。

2) 在亚临界区的气动参数中，接触线的阻力系数高于承力索的阻力系数；接触线的升力系数明显不同于承力索，其升力系数为负值；接触线的斯特劳哈尔数明显低于承力索的斯特劳哈尔数。

3) 传热参数中，接触线因沟槽的存在，其换热性能一定程度上低于承力索的换热性能(约9%以上)。