基于模糊数学和改进遗传算法的滨海地层盾构选型研究

詹金武，黄明，孙春明，王佳程，王更峰

(1. 福建工程学院土木工程学院，福建 福州 350118；2. 福州大学土木工程学院，福建 福州 350116；3. 中铁十一局集团有限公司，湖北 武汉 430061)

随着城市交通拥堵日益严重，越来越多的城市开始修建地铁，以缓解城市交通拥堵问题。盾构法作为城市地铁的重要工法，所选用盾构的地层适应能力及选型成功与否对于工程至关重要。盾构施工的突出特点就是地层的适应性问题，针对不同的土质、施工条件和要求，尤其是在复杂地层条件下，与之适应的盾构类型的选用非常关键[1]。目前，国内外学者针对盾构选型方面开展了相关研究。在盾构选型的定性研究方面，如CORDES 等[2]对隧道沿线土体自西向东分类，重点考虑地下水分布的影响，为巴尔的摩城市红线隧道盾构选型提供依据。RENGSHAUSEN 等[3]讨论了C310 泰晤士河隧道复合土压平衡盾构和复合泥水平衡盾构的优缺点，并进行了风险比较评估，最终选取了复合泥水平衡盾构。SONG 等[4]为了研究土压平衡盾构在膨胀黏土层中的适应性，依托徐州地铁2号线一期工程，提出了盾构选择的目标设计和开挖参数的选择。姚乐[5]针对我国华南地区广泛分布的复合地层，以深圳地铁11 号线车公庙～红树湾和南山～前海湾盾构区间为依托，开展了土压平衡盾构的适应性研究。刘旭全[6]以济南地铁R2 号线烈士陵园站～开源路站为依托，参考国内其他城市类似地层施工经验，获得了适应该地层施工的盾构选型。在盾构选型的定量化研究方面，EDALAT 等[7]采用多标准分析法开展了大不里士城市铁路2 号线一期项目盾构选型的研究。HYUN 等[8]对盾构隧道有关的潜在风险和典型地层进行研究，采用故障树分析(FTA)和层次分析法(AHP)进行了风险分析，并通过实地观测比较验证了该方法。吴贤国等[9]基于TOPSIS 方法开展了地铁施工盾构选型研究，并选取武汉轨道交通2号线进行实例分析，验证了该方法的可行性。黄新淼等[1]通过统计分析法，分析了相关参数与地层之间、相关参数内部之间的差异性和规律性，并将其应用于成都地铁18 号线土建1 标的盾构选型上。这些方法为盾构选型提供了有效建议，但是它们缺少客观的评价标准，易受主观因素影响。因此，亟需建立一个能够综合地评估复杂地层条件下盾构选型的评价方法。因此，本文在前人定性分析盾构选型适应性的基础上，综合考虑滨海地层的适应性影响因素，构建了滨海地层盾构选型适应性评价指标体系；基于改进的遗传算法和层次分析法，得到盾构选型评价指标权重，并确定各评价指标的隶属函数，建立滨海地层盾构选型适应性模糊综合评价模型，对滨海地层盾构选型适应性做出定量评价。

1 盾构选型适应性评价方法研究

1.1 盾构选型综合适应度及评价标准

1.1.1 盾构选型综合适应度计算方法

为了合理地评价由不同地质段构成的盾构区间的盾构选型适应性，特定义综合适应度-D这一概念对其进行评价：

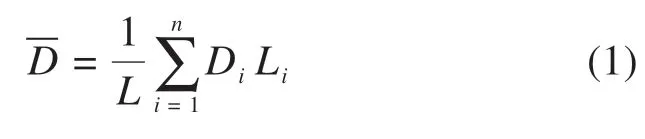
式中：L为盾构区间总长度；Li为盾构区间第i段长度；Di为盾构隧道长度Li的适应度。

1.1.2 盾构选型分级评价标准

在综合分析国内外等级划分方法的基础上，结合滨海地层盾构施工与盾构选型适应性评价实际情况，现将滨海地层盾构选型适应性分为如表1所示的5个评价等级：

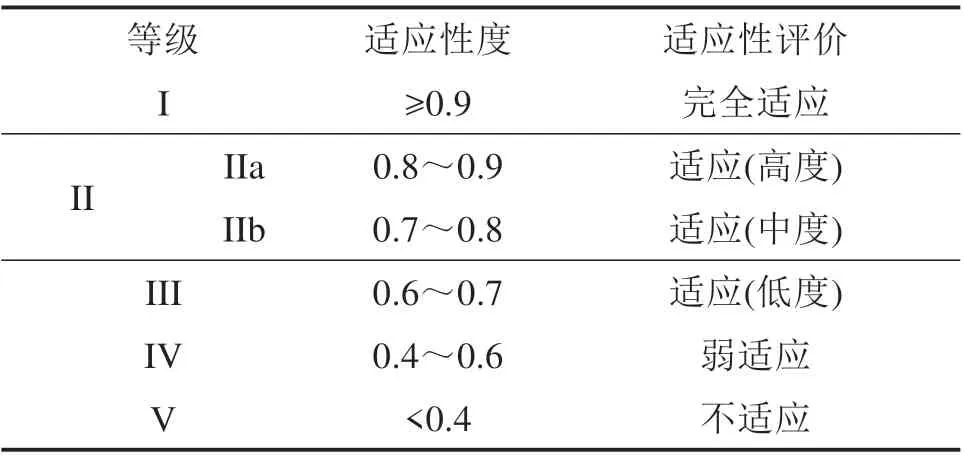
表1 适应度等级划分对照表Table 1 Comparison table of fitness level

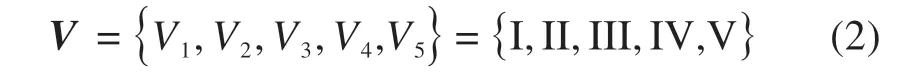
1.2 盾构选型适应性评价指标体系

在考虑盾构选型的依据及原则的基础上，本文重点分析导致盾构掘进困难的各种施工风险源[3]，盾构选型的关键因素主要包括以下3个方面：1)隧道设计参数；2)水文地质条件；3)线路周边环境。

泥水平衡盾构和土压平衡盾构除了维持掌子面稳定的工作原理不同之外，其余设备组成大致相同。因此，隧道设计参数中选取断面直径作为盾构选型的关键性因素，选取水文地质条件中的渗透系数、地层颗粒级配及地下水压作为盾构选型的关键影响因素。盾构掘进时保持建(构)筑物沉降不超限是施工控制中的一大难题，线路周边环境方面选取施工时对地层沉降控制能力作为影响盾构选型的关键性因素。盾构选型适应性评价体系如图1所示。

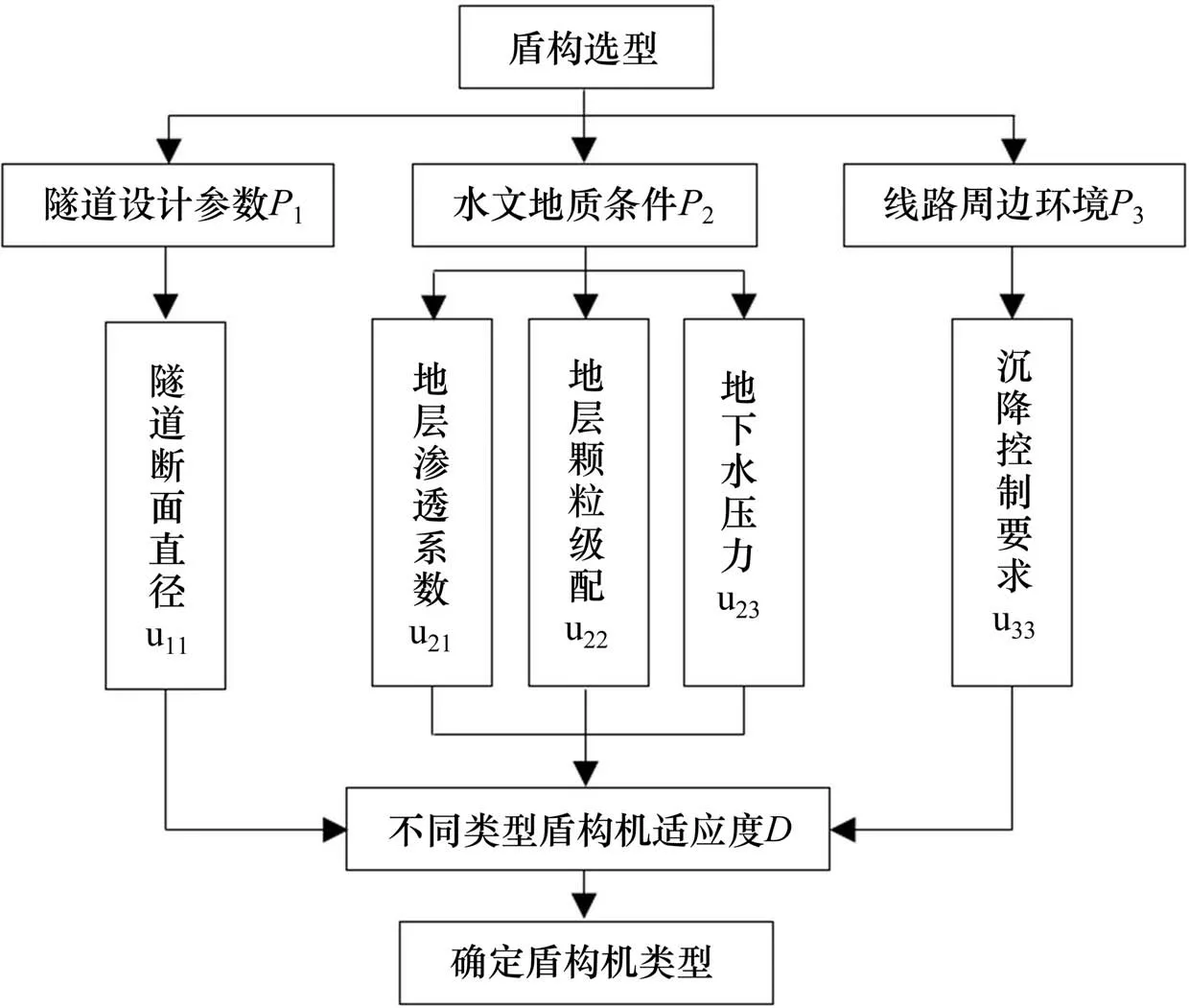
图1 盾构选型适应性评价指标体系Fig.1 Adaptability evaluation system of shield selection

2 基于改进遗传算法指标权重的计算

2.1 基于AHP原理构建权重最优数学模型

2.1.1 改进的遗传算法

根据标准遗传算法的缺点做出针对性改进，增大改进后遗传算法的全局寻优能力及其鲁棒性。改进后的遗传算法实质上是对标准遗传算法的遗传操作中的选择操作、交叉操作及变异操作做了不同程度上的改进。改进的遗传算法流程如图2所示，其参数取值及详细步骤如下所示：

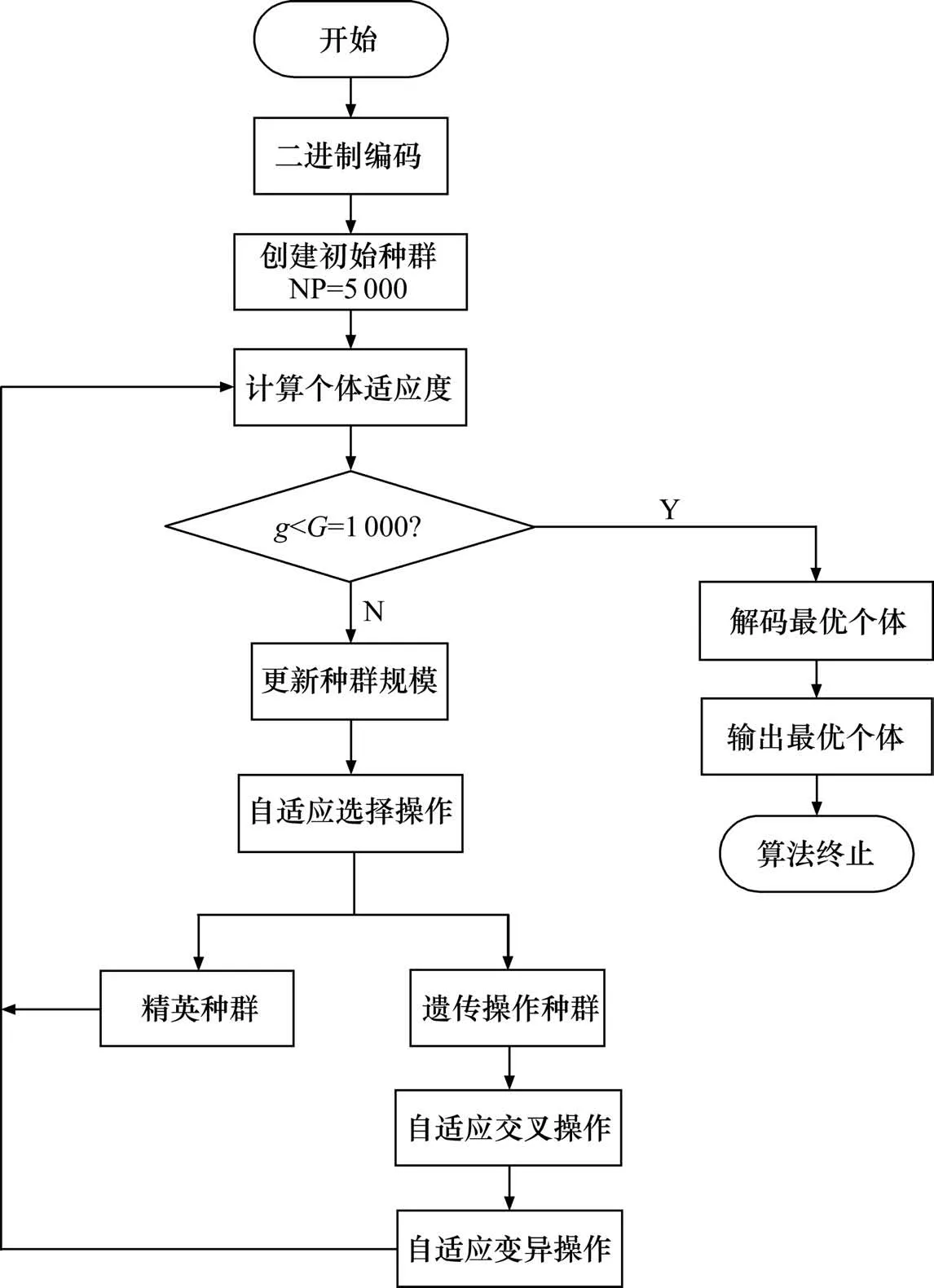
图2 改进遗传算法运行流程图Fig.2 Operation flow chart of improved genetic algorithm

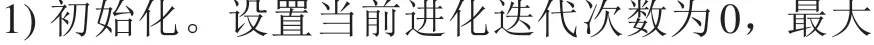
3) 自适应选择操作。将按照个体的适应度排名分为精英种群和进行遗传操作的种群。

4) 自适应交叉操作。采取交叉概率与个体适应度相关的自适应2点交叉算子。

5) 自适应变异操作。采取变异概率与个体适应度相关的自适应随机均匀交叉算子。

6)生成子代种群。将步骤3的精英种群和步骤4，5 的遗传算子生成的种群混合，并按照适应度排名筛选出前5 000个个体。

7) 判断算法是否满足终止条件。经过对改进遗传算法的多次运行发现，算法一般迭代次数达300 代时收敛，为了保守起见，故本文迭代次数设置为1 000，即当迭代次数大于1 000 时，算法结束，解码最优个体，输出目标函数的全局最优解。

2.1.2 构造判断矩阵权重计算数学模型

通常针对目标问题利用专家打分法得到判断矩阵，但因不同专家对目标问题的认识不同和多个影响因素之间的相互影响，往往会使5阶以下矩阵一致性指标满足条件，5 阶以上(包括5 阶)判断矩阵一致性程度较差。

高阶判断矩阵的权重计算多采用层次分析法的特征向量法或和积法，但是对于既定的判断矩阵，不论采取上述2种方法的何种方法其权重及一致性检验指标CR都已经确定，况且得到的权重并不是精确值。因此，根据判断矩阵的构造原理及判断矩阵性质可得到关于判断矩阵最大特征值的表达式(3)；得到关于判断矩阵一致性检验与权重的关系公式(4)，取其最小值即为改进遗传算法(Im‐proved Genetic Algorithm，IGA-AHP)计算最优权重的目标函数，见公式(5)与(6)。

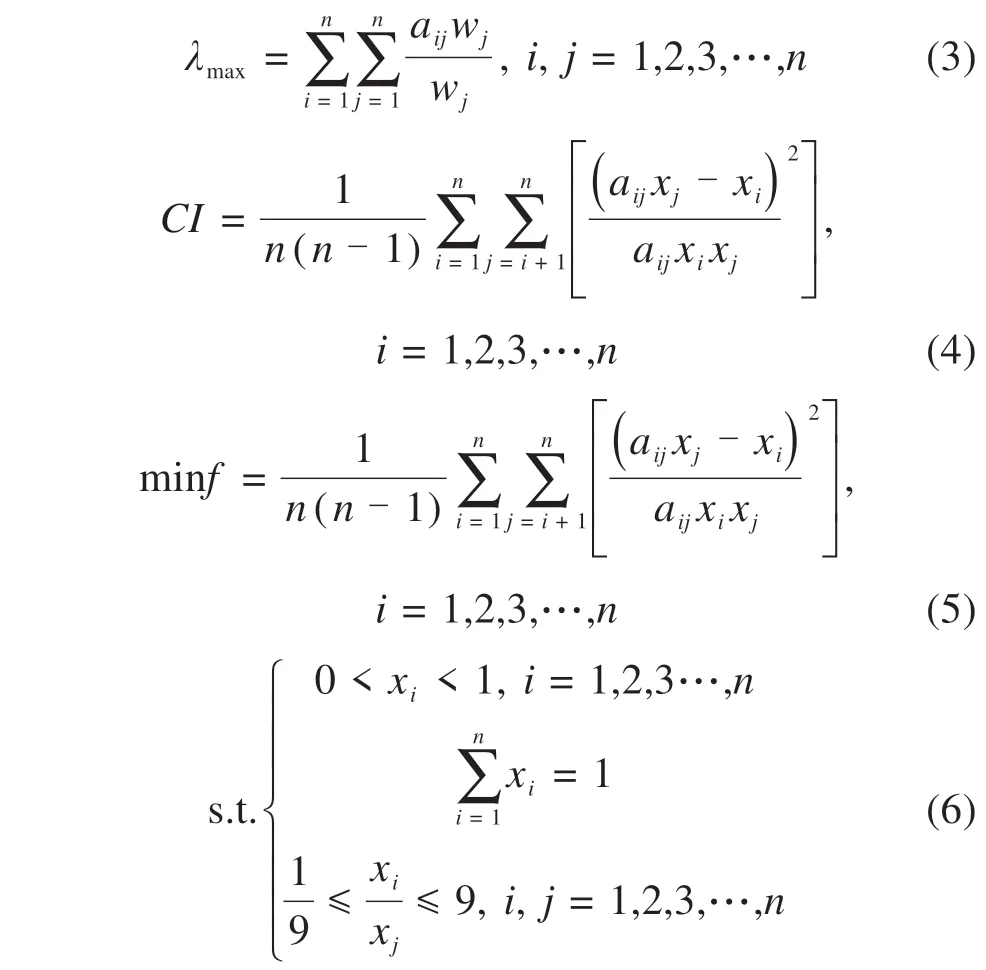
2.2 盾构选型适应性评价指标权重

根据专家的职称和工程经验等将专家分为3个等级，不同等级的专家的评判结果在最终综合的判断矩阵中的占比权重也是不同的，具体权重如表2所示。

表2 不同等级专家评判结果权重占比Table 2 Proportion of weight of expert evaluation results of different grades

设第1 等级(First)的专家共有n位，第2 等级(Second)专家共有m位，第3等级(Third)专家共有k位。根据表2，最终判断矩阵A为：

根据IGA-AHP 计算得到判断矩阵A的一致性指标值CI=0.028 3，计算得到其一致性比率CR=0.049<0.1，因此，盾构选型适应性评价体系准则

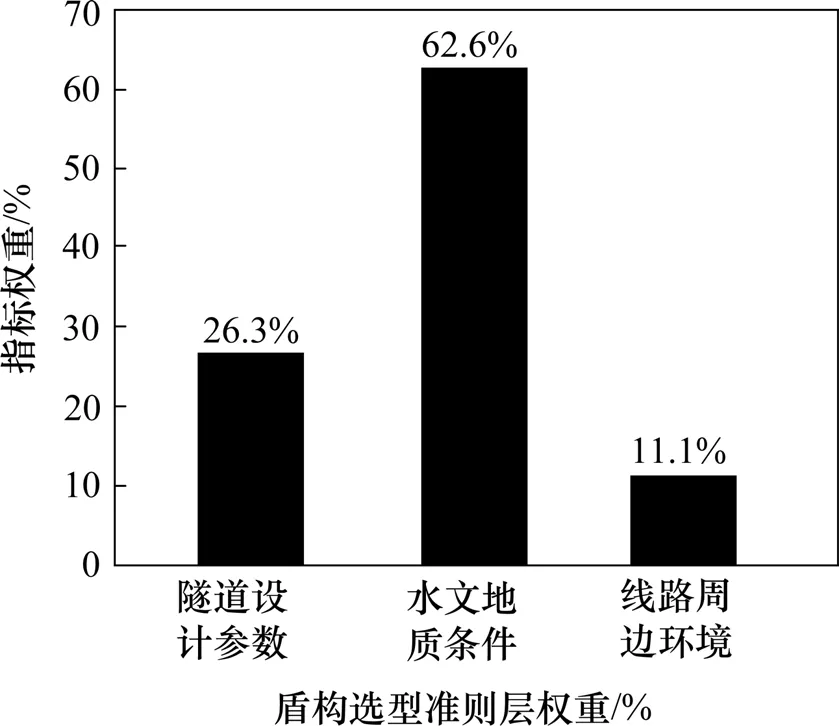
图3 盾构选型准则层的指标权重Fig.3 Index weight of shield selection criteria layer

2)盾构选型指标层的评价指标权重

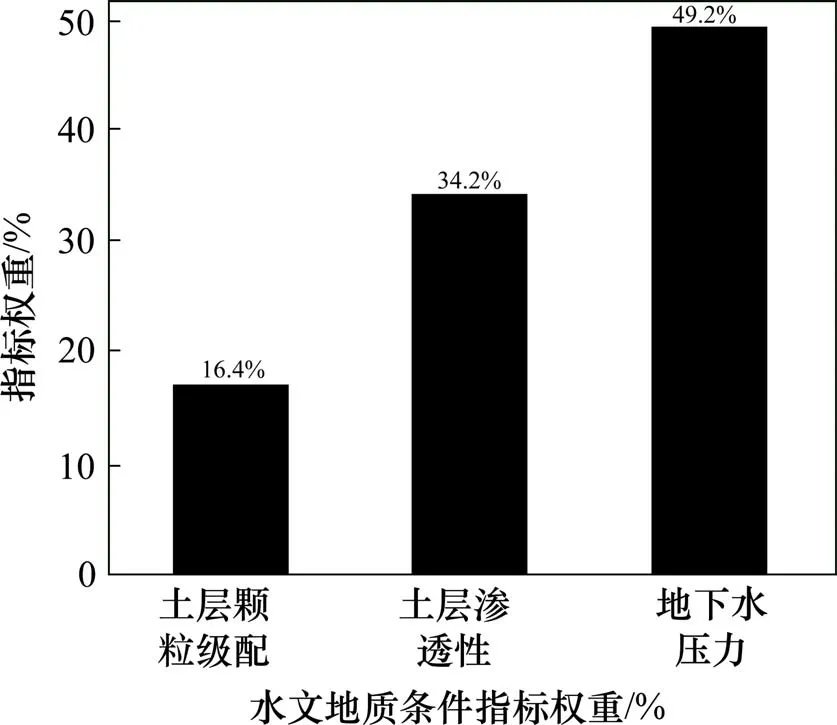
图4 水文地质条件指标层权重Fig.4 Index layer weight of hydrogeological conditions

2.2.2 总层次排序评价指标权重

根据计算得到盾构选型评价指标层次总排序的一致性检验指标CR和层次总排序权重如表3所示。

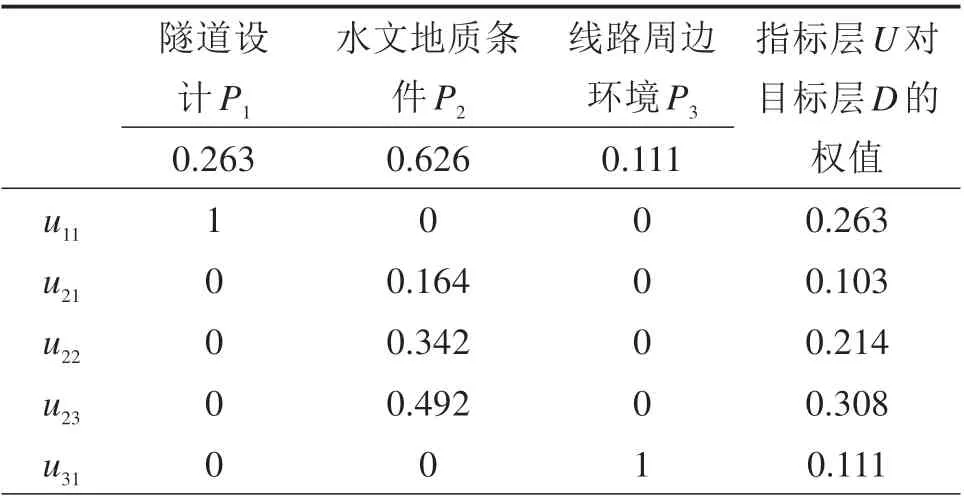
表3 盾构选型评价指标层次总排序权重Table 3 Total ranking weight of shield selection evaluation index levels

由表3 及图5 可知，盾构选型评价指标的层次总排序一致性比率CR满足一致性检验，盾构选型评价指标权重从大到小依次为地下水压力(u23)，隧道断面尺寸(u11)，地层渗透系数(u22)，沉降控制要求(u31)，土层颗粒级配(u21)。

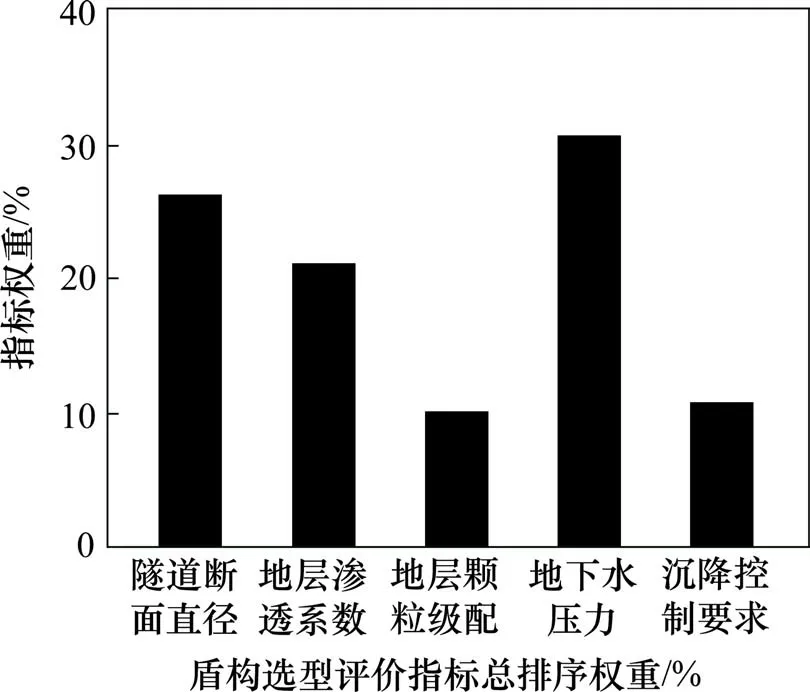
图5 盾构选型评价指标总排序权重Fig.5 Overall ranking weight of shield selection evaluation index

3 盾构选型评价指标隶属函数

根据前文所构建的盾构选型适应性评价指标体系，分别构建泥水平衡盾构(Slurry Pressure Bal‐ance Shield，SPB)和土压平衡盾构(Earth Pressure Balance Shield，EPB)的隶属函数。

3.1 隧道设计评价指标隶属函数

盾构隧道施工时，盾构掘进不可避免地会对前方开挖土体造成扰动，隧道断面尺寸越大，其对土体造成的扰动越大。地铁运营要求盾构隧道的直径不能过小，直径在6～7 m 之内的盾构隧道已经逐渐不能满足要求，直径7～8 m 的中型断面已逐渐成为主流[10−11]。同时，在盾构机的类型上，超大直径SPB 的数量远超过EPB，通常来说，直径超过13 m 的超大直径盾构隧道开挖一般优先考虑使用SPB。截止目前，最大的SPB是中国香港屯门−赤鱲角隧道，盾构机开挖直径达17.6 m；最大的EPB 为美国西雅图隧道，盾构机开挖直径达17.48 m。因此，构建盾构选型评价指标中隧道断面尺寸对应不同模式盾构的隶属函数如表4所示。

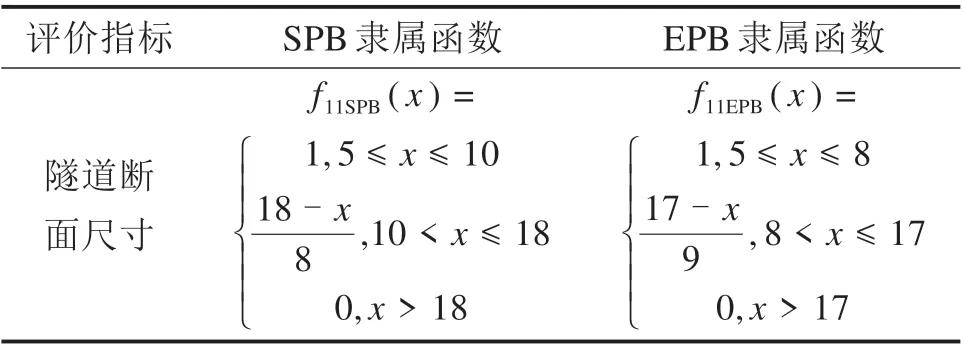
表4 不同模式盾构对应隧道断面尺寸的隶属函数Table 4 Membership function of section size of corresponding tunnel of shield machine in different modes

3.2 水文地质条件评价指标隶属函数

3.2.1 土层渗透性

根据大量施工经验给出的不同盾构类型与土层渗透系数之间的对应关系，当土层渗透系数大于10-4m/s 时，此时可选用SPB；当土层渗透系数在10−7～10−4m/s 之间时，可根据实际情况选用SPB，也可以对渣土进行改良选用EPB。根据现场盾构施工实例，一般认为EPB 作业的土层渗透系数上限为10−5m/s[12]。

3.2.2 土层颗粒级配

一般说来，若盾构掘进土层中细颗粒的含量在40%以上时，此时可选用EPB；相反的，适宜选用SPB。细颗粒粒径的以0.075 mm 作为界限。在实际盾构施工中，若土层中细颗粒含量少于30%，对渣土进行改良后，也可以选用EPB，且EPB 螺旋输送机形成止水壁的细颗粒含量最低也是30%～35%[13]。

3.2.3 地下水压力

若盾构掘进地层的地下水压力大于0.3 MPa时，可以选用泥水平衡盾构，而对于地下水压能击穿泥膜的最大数值没有具体的规定。根据盾构施工实例[14]，地下水压力不超过0.6 MPa 时几乎不会对泥水平衡盾构造成影响。若盾构掘进地层的地下水压力值小于0.3 MPa，宜选用土压平衡盾构。但若土压平衡盾构通过加长螺旋输送机的长度或者采用二级螺旋输送机也可以在地下水压力不大于0.55 MPa 的地层中掘进[15]。综上，构建水文地质条件对应不同模式盾构的隶属函数见表5所示。

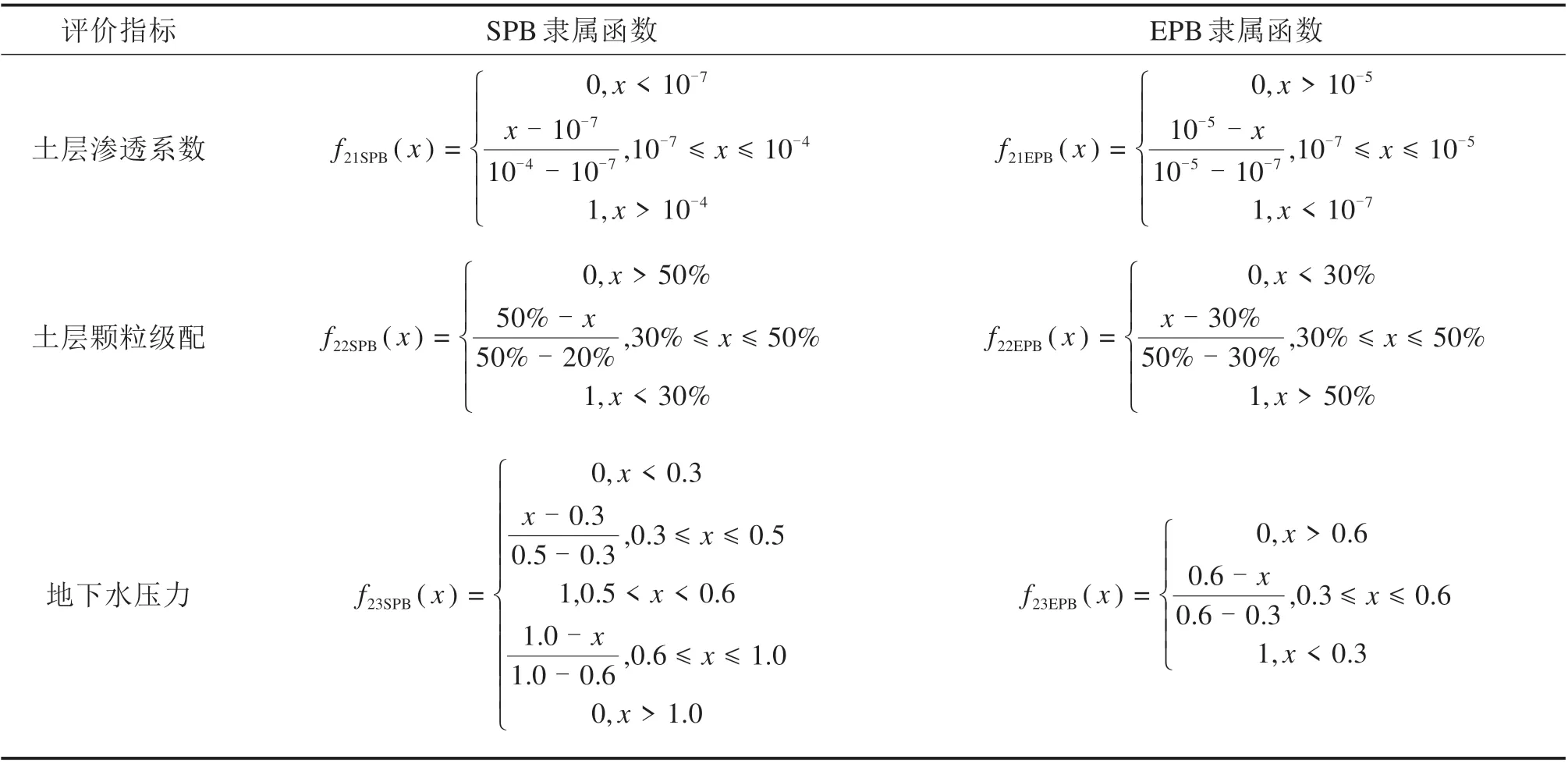
表5 不同模式盾构对应水文地质条件指标的隶属函数Table 5 Membership function of hydrogeological condition indexes corresponding to shield machines in different modes

3.3 线路周边环境评价指标隶属函数

盾构开挖时不可避免地会对地层造成扰动，继而产生地表沉降，地表沉降过大或者沉降区域不均匀，极易导致近接建(构)筑物损坏。根据盾构施工实际经验[16]，土压平衡盾构能够较容易地把地表沉降值控制在10 mm 以内；而泥水平衡盾构施加的泥水压力控制精度为±0.1 MPa，其应对掌子面水土压力的变化更为灵敏，能够把地表隆沉控制在5 mm 以内。据此，构建了地下水压力对应不同模式盾构的隶属函数如表6所示。

表6 不同模式盾构对应地表沉降控制值的隶属函数Table 6 Membership function of ground settlement control values corresponding to shield machines in different modes

4 盾构选型适应性评价实例验证

4.1 盾构选型适应性模糊综合评价模型

将模糊数学方法应用到盾构选型适应性评价中，通过隶属度将盾构选型的模糊性转化为确定性。

式中：B为O的综合评判值集合，Di为评价目标Oi的适应度；A为评价指标U的总排序权重集；R为U对O的隶属度矩阵。

基于模糊综合评价方法构建了盾构选型适应性评价指标体系，引入改进的遗传算法求解最小一致性指标下评价指标的总层次排序。最终结合盾构选型适应性评价指标体系及各评价指标的权重和隶属函数，如表7所示，为所建立的盾构选型适应性模糊综合评价模型的相应参数。

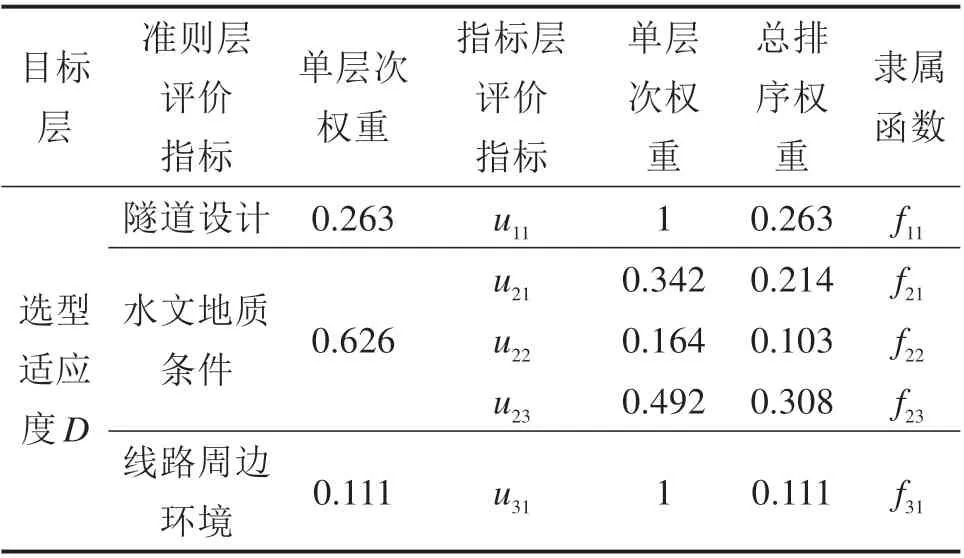
表7 盾构选型适应性模糊综合评价模型Table 7 Fuzzy comprehensive evaluation model of shield selection adaptability

4.2 实例验证

4.2.1 工程概况

厦门市轨道交通4号线彭厝北站～蔡厝站区间起始于厦门市翔安区新店镇彭厝北，沿在建翔安西路由西向东敷设，沿线地面现状主要为在建翔安西路施工工地，两侧为农田及荒地，彭蔡盾构区间平面位置示意图如图6所示。

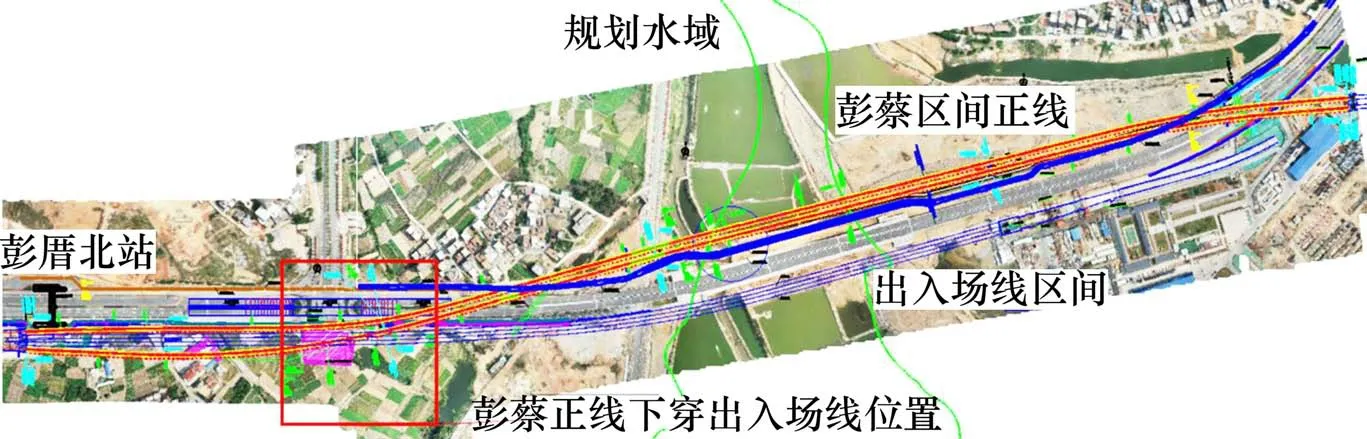
图6 厦门地铁4号线彭蔡区间平面示意图Fig.6 Plan of Pengcai section of Xiamen Metro Line 4

区间右线起讫里程为右DK57+011.156～右DK59+197.857，右线全长2 186.701 m；左线起讫里程为左DK57+011.156～左DK59+199.422，左线全长2 188.266 m，区间采用盾构法施工。区间分别在里程ZDK57+534，ZDK58+057，ZDK58+588

设联络通道3 座。其中2 号联络通道兼作废水泵房。区间现状覆土厚度为10～21.4 m。

4.2.2 盾构选型适应性评价分析

本文选取右线区间进行盾构选型适应性评价分析，先对盾构选型适应性评价指标取值，根据盾构掘进区间分段原则，将彭蔡盾构区间右线盾构选型分为6个区段进行适应性评价。彭蔡盾构区间右线不同区段指标取值结果如表8所示。

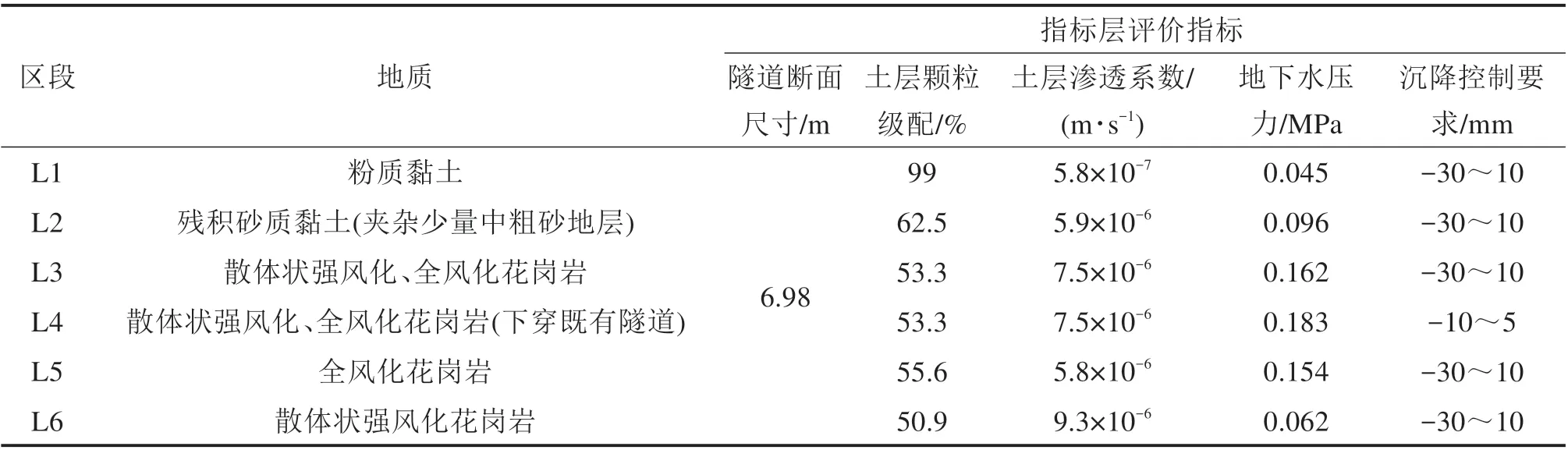
表8 彭蔡盾构区间右线不同区段盾构选型评价指标值Table 8 Evaluation index values of shield selection in different sections of right line of Pengcai shield interval

对盾构选型适应性综合评价，将彭蔡区间右线盾构选型评价指标的取值代入与之相对应的隶属函数，分别构建2 种盾构类型的隶属度矩阵REPB，RSPB及相应的权重矩阵A，根据式(8)，计算得到不同类型盾构第i分段适应度值Di及综合适应度-D，如表9～10所示。

通过表9～10可知，彭蔡盾构区间选用土压平衡盾构的综合适应度为0.86，评价结果为高度适应；选用泥水平衡盾构的综合适应度为0.39，评价结果为不适应。基于盾构选型的综合适应性评价结果可知，彭蔡盾构区间应选用土压平衡盾构，此评价结果与彭蔡区间选用土压平衡盾构掘进一致。

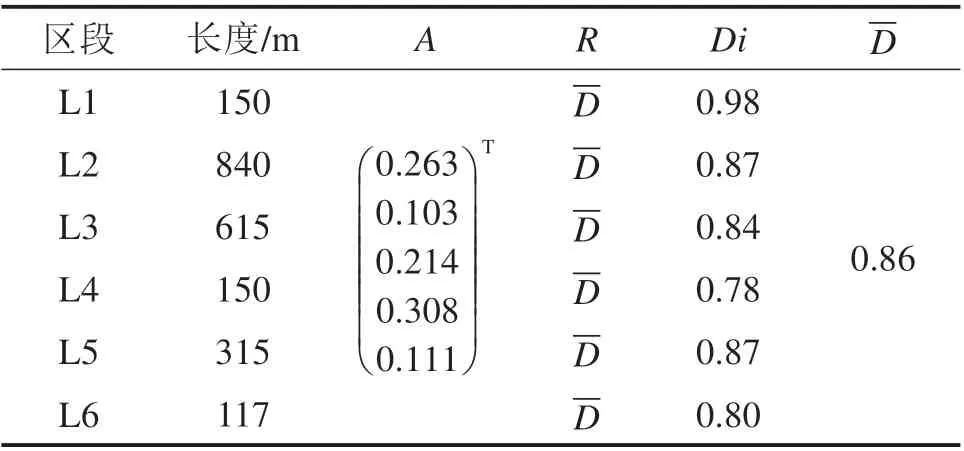
表9 彭蔡区间右线土压平衡盾构适应度Table 9 Adaptability of EPB shield in right line of Pengcai section

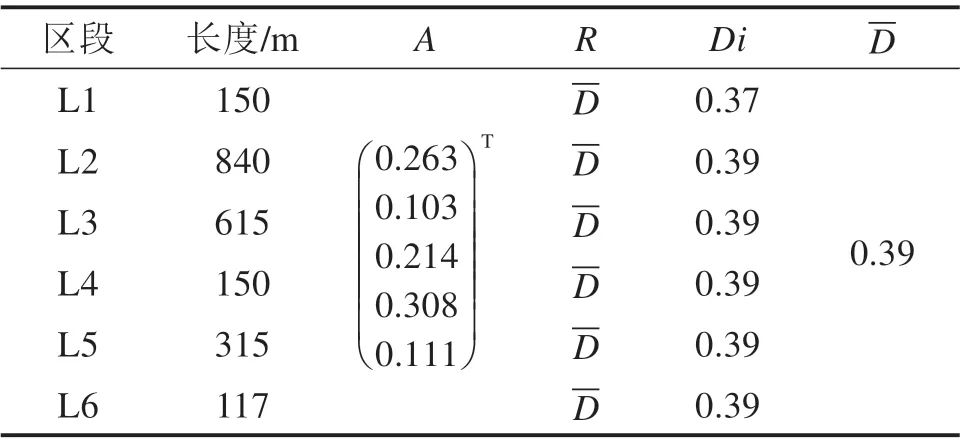
表10 彭蔡区间右线泥水平衡盾构适应度Table 10 Adaptability of slurry balance shield on the right line of Pengcai section

5 结论

1) 确定了盾构选型适应度的计算方法和分级标准；根据国内外盾构施工实际工程经验，从隧道设计、水文地质条件、线路周边环境3个方面建立了盾构选型评价指标体系。

2) 采用改进遗传算法及AHP(IGA-AHP)确定评价指标的层次单排序权重和层次总排序权重，得到指标层U对目标层D的权值分别为0.263(u11)，0.103(u21)，0.214(u22)，0.308(u23)，0.111(u31)，总排序一致性比率CR=0.049<0.1，满足一致性检验要求，且权重结果符合实际，表明采用IGA-AHP 模型计算权重结果的准确性；同时，采用模糊数学构建各个评价指标的隶属函数，得到盾构选型的隶属度矩阵。

3) 通过彭蔡区间现场施工的参数和数据，对所构建盾构选型评价模型的有效性进行了验证，分别得到不同类型盾构的分段适应度值Di，最终取得彭蔡盾构区间选用土压平衡盾构的综合适应度-D为0.86，为高度适应；选用泥水平衡盾构的综合适应度-D为0.39，为不适应，表明土压平衡盾构适用于该区间掘进，这与实际工程的选择相符。

4) 将模糊数学和改进遗传算法应用于盾构选型适应性评价中，仍有不少问题有待解决，例如考虑更全面的因素，建立更完善的评价指标体系；同时，后续将进一步开展基于人工智能方法的盾构选型评价方法的研究，应用大数据驱动知识进行学习、推理等。