基于改进型D3QN深度强化学习的铁路智能选线方法

2022-03-30袁泉曾文驱李子涵高天赐杨冬营何庆

铁道科学与工程学报 2022年2期

袁泉，曾文驱，李子涵，高天赐，杨冬营，何庆

(1. 广州地铁设计研究院股份有限公司，广东广州 510010；2. 西南交通大学土木工程学院，四川成都 610031)

选线是铁路建设的龙头，也是决定工程项目的投资成本、难易程度和安全风险的首要因素[1]。传统的人工选线方法多为设计人员凭经验手工设计线路，存在方案有限，决策周期长，劳动强度大等缺陷[2]。随着我国铁路建设重心由东部向中西部山区转移，研究区域内愈加频繁地出现丘陵河谷等复杂地形及地质不良、环境敏感区等复杂区域，传统选线方法的缺陷更加明显，极大限制了线路规划设计的效率与质量。因此，亟需将传统选线理论与飞速发展的人工智能技术结合，开展铁路智能选线方法研究。智能选线方法，是一种将选线理论与地理信息系统、智能计算、多目标优化等结合的现代线路设计方法，旨在利用计算机自动搜索出连接起、终点，满足限制条件且目标函数最优的线路方案，能为设计人员提供多样化的线路备选方案，可有效提高选线工作的速度和质量[1-2]。国内外学者运用多种方法对铁路智能选线展开研究。变分法[3]将线路优化变为寻求函数积分值最小的空间曲线的数学问题；网格规划法[4]将研究区域划分为一系列网格并采用最优路径等算法搜索出连接起、终点的最优方案；动态规划法[5]将起终点连线划分为多个区间，将线路优化问题分解为多个阶段进行求解；易思蓉等[6−7]引入知识工程，基于最优路径分析和知识推理自动生成路径；LI 等[8−10]将改进距离变化算法与遗传算法结合，遵循由面到带、由带到线的思想分2阶段实现复杂山区环境的线路智能优化。铁路选线是复杂、全面的系统工程，设计人员实际需要对线路整体进行评价。现有的智能选线方法，大多强于局部计算，对后续未知以及全局态势的感知把控较弱[1]。近年来，深度强化学习(Deep Reinforcement Learning,DRL)在智能控制、工业制造等领域备受关注[11]，其具有基于全局的迭代更新方法和随机搜索策略，使智能体在一定程度上具备了“大局观”，已被广泛应用于机器人路径规划、运营优化领域[12−15]。鉴于此，本文基于深度强化学习理论，结合强化学习的决策能力和深度学习的感知能力，提出面向铁路选线的深度强化学习模型，以最小化工程建设的经济费用作为目标，考虑多种线路约束条件，沿途自动布设桥梁、隧道、路基等构筑物，得到线路走向的优化方案，有助于提高铁路线路的设计效率。

1 深度强化学习算法与智能选线模型

1.1 强化学习原理

强化学习的原理模型如图1所示。设定在环境中有一个能执行行动策略的个体，称之为智能体Agent。在t时刻，智能体感知当前环境的状态信息st，通过策略输出动作at。Agent 执行动作at作用于环境并迁移至新状态st+1，同时接受环境向其反馈的奖励信号r(st,at)进而展开新一轮循环。智能体通过与环境的不断交互试错积累经验、调整策略，最终使其得到最优的行动策略，以在完成任务时获得最大的累积奖励。

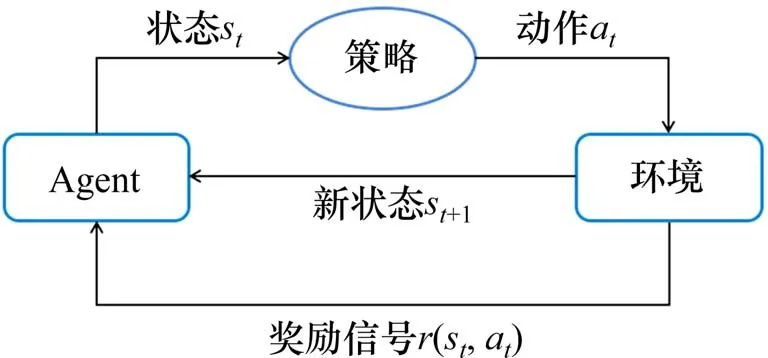
图1 强化学习理论框架Fig.1 Theory framework for reinforcement learning

Q-Learning(QL)算法是一种经典的强化学习方法，它将智能体与环境交互得到的经验记录在一张Q 表(Q-Table)，将动作和状态作为2 个维度的索引，表中记录行为价值函数Q用以评估在不同状态执行各个动作的好坏。行为价值函数Q更新如式(1)：

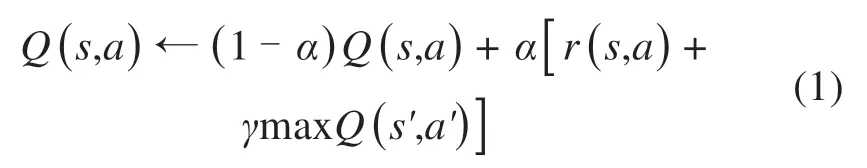
其中：α和γ取值范围均在[0,1]。α为学习率，表征Q值发生改变时更新变化的速度，α越接近1 则每次Q值更新的幅度越大；γ为折扣因子，代表智能体重视未来收益的程度，γ接近1 表示智能体更专注获得长期奖励，不局限于当下采取动作获得的即时收益。在Q表中的每个状态—动作对都被访问更新足够次数后，Q表收敛，智能体将在完成任务时获得最大的累计奖励。

1.2 铁路智能选线模型

本节从模型环境、状态、动作、奖励、约束条件、探索策略等方面构建面向强化学习的铁路智能选线模型。

1.2.1 环境空间

铁路选线的设计区域是连续广阔的三维地理空间，模型环境若为连续状态，线路走向在其中将有无数种可能，智能体难以完成线路搜索任务。为此，利用GIS 系统的数字高程模型(DEM)，将连续空间离散成一张具有三维数字高程信息的规则栅格地图；向地图添加起点、终点、地质不良区、环境敏感区等空间属性Ci，得到具有属性信息的三维空间点集E，作为选线模型环境。

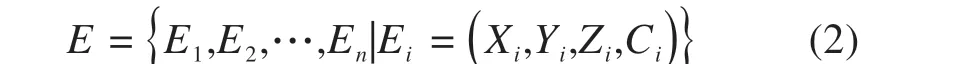
Li=(Xi,Yi)为智能体位置的平面坐标，Zi为所处位置地面高程，Ci为属性信息。模型中所有点属性信息分为3 类：抵达终点的状态Attain；将环境敏感区、地质不良区设置为禁行区域，其不可连通状态Forbid；其他可通行状态Normal。

1.2.2 状态空间

路径规划问题将小车简化为质点，小车所处位置Li=(Xi,Yi)即可视为环境中的一个状态。然而，智能选线的任务是搜索符合线路标准的线形，要避免智能体与环境交互时出现曲线半径过小甚至列车不能通行的过大转角。若以单一位置作为智能体状态，即使在同一位置Li发生同一状态转移到达位置Li+1，Li前一步位置Li-1的不同亦会导致截然不同的转角，如图2所示。因此列车不能简化成质点，其长度不能忽略。

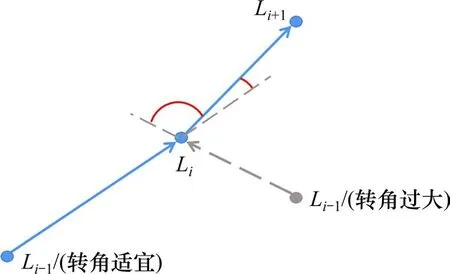
图2 单一位置导致的转角差异Fig.2 Different angles caused by single location

本模型将前后2个位置联结，以此线元作为智能体的一个状态，每个转角只由前后2 个线元决定。智能体由起点出发抵达终点，得到的是由若干线元组合成的初始线形。状态空间S表示环境中所有线元的集合。

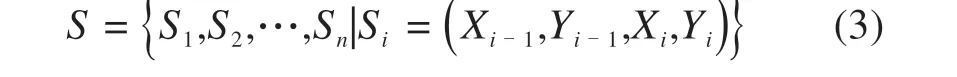
1.2.3 动作空间

对铁路选线而言，智能体的探索步长li不宜过小。一方面，过小步长严重影响模型收敛速度，另一方面，相邻位置间距太小会使线形出现不符实际的毛刺、转角。故选用栅格精度30 m 的DEM模型，智能体每步跨越N个高程点，N为可变的超参数。虽然一个位置有东、西、南、北、东北、西北、东南、西南8个方位供选择，但为使线路转向平缓，动作空间Ai只创建相对当前走向左前、正前、右前3 个方向的动作(图3)。状态更新方式如式(4)，aix，aiy分别为动作ai2个方向上的分量。

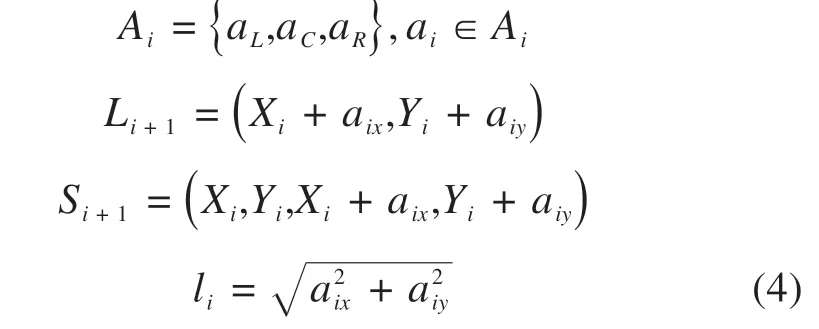
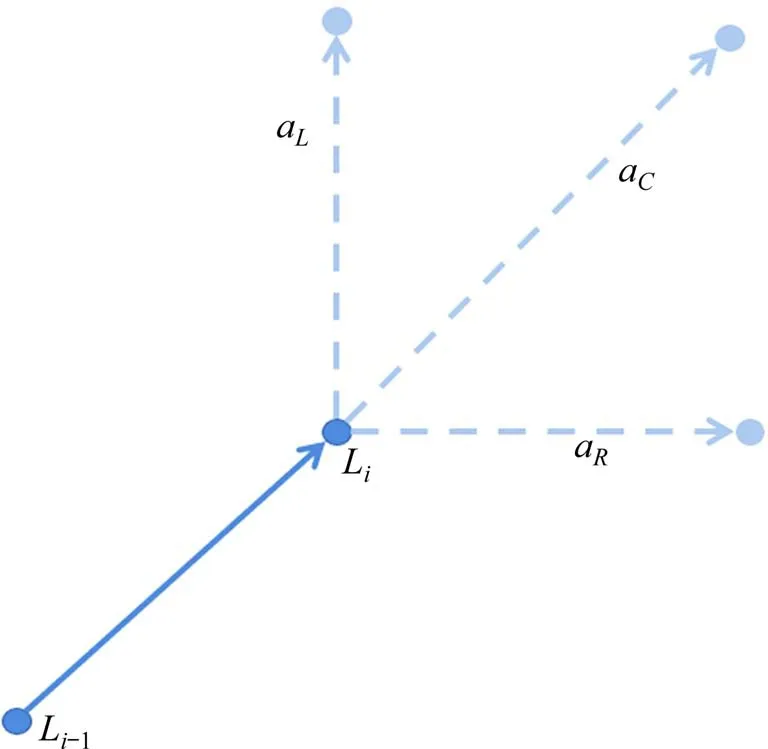
图3 创建三向动作Fig.3 Create three-way action

1.2.4 奖励函数

智能体收到来自环境的奖励信号Ri由2 部分组成：

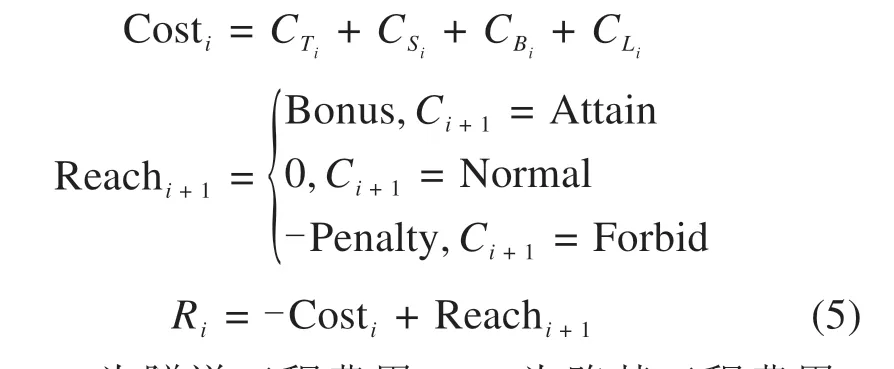
式中：CTi为隧道工程费用；CSi为路基工程费用；CBi为桥梁工程费用；CLi为与线路长度有关的轨道、通信、电力等方面的费用；Costi为状态Si转移到Si+1对应的工程造价；Reachi+1为根据新状态Si+1属性分别给出的反馈值。智能体到达终点获得额外的正值奖励Bonus；进入禁行区域得到惩罚Penalty，并重新开始新一轮探索。在其余的可连通区段，不获得额外反馈，继续进行本轮探索。

1.2.5 约束条件

1)设置最大展线系数γmax，每轮线路搜索所有线元长度总和不应超过γmax与线路起、终点直线距离lSE的乘积。

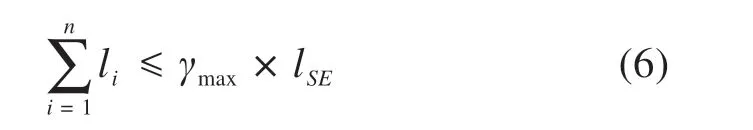
2) 线路上所有点的集合P与禁行区域交集为空。

3) 在得到初始线形后，逐一添加拟合时能有效利用的交点，直到因交点过于密集而无法满足规范要求的最小曲线半径、圆曲线长度、夹直线长度等约束条件。随后将其拟合并配置曲线以生成最终线路方案[8-9]。

1.2.6 探索策略

采用ε- greedy策略作为智能体动作选择策略，ε为贪婪度，取值于0～1之间。行动时，智能体以ε的概率从可行动作中随机选择，以1-ε的概率选择当前行为价值最大的动作。在探索初期，智能体积累的环境经验较少，故以较大的ε更多地随机探索环境，避免陷入局部最优。随着探索次数的增多，令ε逐渐减小，更多地选择行为价值最大的动作，更好地利用环境经验。

1.3 深度强化学习算法与改进

1.3.1 Deep Q Network算法

当状态和动作空间简单、维数不高时，可以用Q-Learning 方法将行为价值函数Q存储在表格。但状态和动作复杂高维时，此方法会带来维数灾难，不再适用。因此，有学者提出一种将深度学习出色的感知能力和强化学习的决策能力结合的深度强化学习(Deep Reinforcement Learning, DRL)算法。选用深度神经网络Q(s,a;θ)对Q表进行函数拟合；θ为神经网络参数。神经网络输入状态向量，输出每个动作对应的价值函数。此法称为深度Q 网络(Deep Q Network, DQN)算法[15]。本文将DQN 算法的变体Dueling-Double DQN(D3QN)用于铁路智能选线研究。

1.3.2 Dueling-Double DQN算法

Q-Learning算法在探索的每一步都查询利用下一状态最大的状态-动作对maxQ(s',a')对Q(s,a)进行更新。这个思路直接用于DQN会出现如下问题：

1) 训练神经网络的前提是假设训练数据独立同分布，而智能体交互得到的顺序数据之间存在很强关联性，易造成网络训练不稳定。

2) DQN 网络的参数θ不断更新，用同一网络生成Q(s,a)和maxQ(s',a')导致神经网络的时序差分目标不断变动，不利于算法的收敛。

3) 训练过程前期模型不够稳定，值函数估计存在偏差，使用maxQ(s',a')会导致模型过高估计某一动作的预期收益，误导智能体选择错误动作导致模型无法找到最优的策略。

对上述问题，D3QN算法做出以下改进：

1) 使用经验重放机制(Experience Replay)将交互得到的经验逐条存储在经验池中，积累到一定数量后，模型每步从经验池中随机抽取一定批次的数据训练神经网络[15]。随机抽取的经验打破了数据之间的关联性，提高泛化性能，有益于网络训练稳定。

2)构造2 个结构相同的神经网络[16]，分别为估值网络QE(s,a;θ)和目标值网络QT(s,a;θ')。估值网络用于选择动作[17]，参数θ不断更新；目标网络用于计算时序差分目标值Y，参数θ'固定不动，每隔一段时间替换为最新的估值网络参数θ。目标值Y计算公式如下：

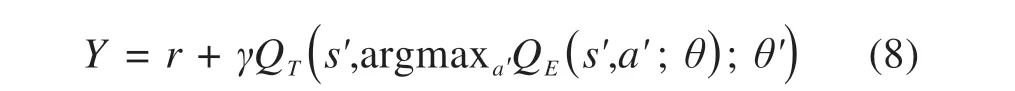
θ'一段时间内保持不变导致估值网络QE收敛目标Y相对固定，有益于收敛；估值网络和目标值网络产生的最大值函数的动作不一定相同，用QE产生动作，QT计算目标值，能避免模型选到被高估的次优动作，有效解决DQN算法的过估计问题。

3) 对神经网络结构做出改进，将其输出端分流为2 部分[18]。一部分为表征各状态好坏的状态值函数V(s;θ,μ)，另一部分为区别特定状态各动作好坏的优势函数A(s,a;θ,ω)：

改进后得到的D3QN算法流程如图4所示。

图4 基于D3QN的铁路智能选线算法Fig.4 Intelligent railway location design algorithm based on Dueling-Double DQN

2 案例分析

以我国西南某山区铁路为例，对本文提出的方法进行验证。智能选线算法模型参数如表1所示。

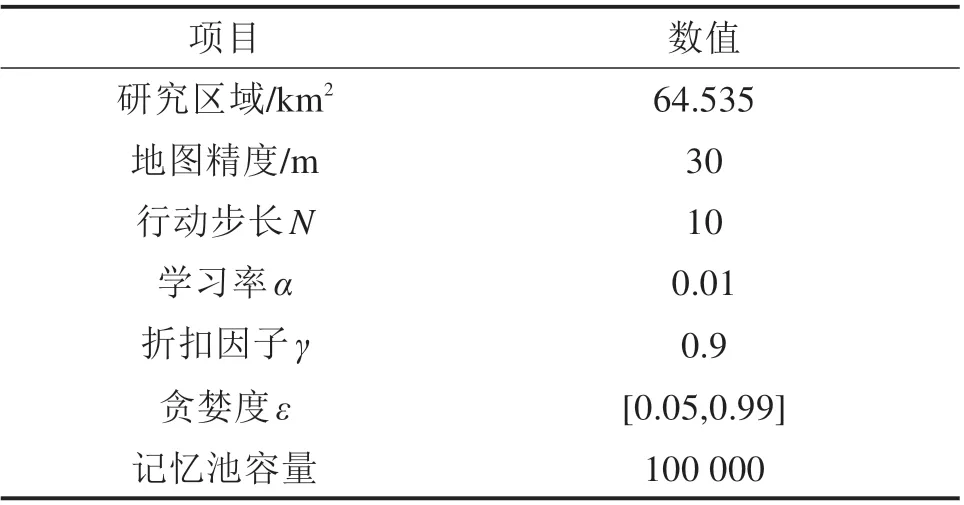
表1 模型参数Table 1 Model parameters

智能体在环境中探索十万个回合后，得到2 171 条备选方案。选取2 条具有代表性的线路方案，与人工定线方案对比(图5)。人工定线方案线路全长11.07 km，建设费用16 934.8 万元；智能选线方案1 为最优方案，全长11.32 km，预计花费14 046.2 万元，较人工定线方案节省17.5%，桥梁建造长度缩减34%。智能选线方案2 为人工方案与最优方案的折中选择，较最优方案适当放大了桥梁配比，经济费用较人工方案节省11.3%，线路全长较最优方案更短。智能选线方案与人工方案走向大致相同，但在跨越河流时体现出差异。人工方案以大半径曲线直接横穿河谷，需建造较长桥梁，因此耗资较大；智能选线方案以小半径曲线蜿蜒绕行，找到了平衡路基长度和桥梁长度的最佳过河桥位，节约了大量建设费用。