高速磁浮列车−柔性轨道梁横向耦合振动

2022-03-30王淼宋振森滕念管

铁道科学与工程学报 2022年2期

王淼，宋振森，滕念管

(1. 上海交通大学船舶海洋与建筑工程学院，上海 200240；2. 上海市公共建筑和基础设施数字化运维重点实验室，上海 200240)

开发时速600 km/h 以上的磁浮轨道交通系统可填补高铁与航空运输之间的速度空白，为中长距离的地面旅客运输提供新的选择。高速磁浮多采用“以桥代路”的设计思路，由于轨道梁细长，随着行车速度提高列车与轨道梁之间会产生明显的耦合振动。对此，众多学者通过建立磁浮车−桥耦合振动模型进行了深入研究。TENG 等[1]建立了考虑自动控制器的10 自由度磁浮列车-3 跨连续梁竖向耦合振动模型，研究了轨道梁各项参数及车速对系统耦合振动的影响。REN 等[2]建立了6 自由度的车−桥竖向耦合振动模型，数值模拟结果表明，相较于轨道梁振动，轨道不平顺对车体振动加速度具有更明显的影响。倪萍等[3]分别建立了10自由度车辆及轨道梁的竖向耦合振动模型，并基于PID 控制对二者进行耦合，研究了时速600 km/h磁浮系统的振动响应。目前，单独针对磁浮车−桥竖向耦合振动的研究较为多见，而对于时速600 km/h 以上的高速磁浮横向耦合振动却关注较少。由于磁浮系统在水平横向没有重力荷载作用，此时轨道不平顺作为主要的激励源，对系统振动起着决定性影响。在横向荷载方面，LIU等[4−5]研究了侧风作用下列车的空气动力学特性，表明列车在运行中会受到较大的风致横向荷载作用。而列车−控制器−轨道梁作为一个耦合的整体，有必要建立完整的横向耦合振动模型，对轨道梁的横向动力性能加以验证。本文通过理论推导，建立了基于PD 控制器的246 自由度高速磁浮列车−40 跨柔性轨道梁横向耦合振动微分代数方程组统一模型，并通过编程进行数值求解，针对某新型轨道梁，研究在侧风、轨道不平顺荷载共同作用下的车−桥横向耦合振动，进而考察该轨道梁的横向动力学性能。

1 车桥横向耦合振动模型

1.1 模型概述

图1 为横向耦合振动示意图，其中摆杆(属二系悬挂)连接车体与悬浮架，橡胶弹簧连接悬浮架与导向电磁铁，轨道梁与电磁铁之间由基于自动控制器的磁浮吸力来实现稳定的磁浮间隙。当车体与悬浮架在横向产生相对位移时，由摆杆提供横向回复力[6]，另设有辅助限位弹簧以避免二者相对横向位移过大，因此摆杆转角较小，故将摆杆及辅助限位弹簧的回复力做线性化处理。

图1 横向耦合振动示意图Fig.1 Schematic diagram of lateral coupling vibration

如图2所示，轨道梁受移动的磁浮力作用，在水平方向上由于轨道方向不平顺及轨距不平顺的存在，会在梁两侧分别对磁浮间隙产生扰动，进而引起车−桥横向耦合振动。在工程中电磁力为均布移动荷载，本文采用单侧78 个，双侧共156 个移动集中荷载模拟均布电磁力。如图5所示，根据反演的轨道不平顺谱可知，里程长度在1 km 左右足够覆盖不平顺的峰值及各种波长，故选择对应的轨道梁数量，即40跨简支梁建立模型。

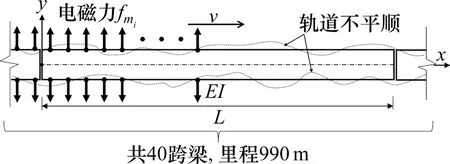
图2 轨道梁示意图Fig.2 Schematic diagram of track beam

1.2 车辆振动方程

图3 为高速磁浮TR08 车型的横向振动计算简图，将车体、悬浮架及导向电磁铁视为刚体并考虑其水平运动、摆头运动，悬浮架由铝合金制成，其纵梁具有一定的弹性[7]，故将悬浮架的前后2 个单元视为由弹簧阻尼器连接的刚体，5 列编组列车共246个广义自由度。

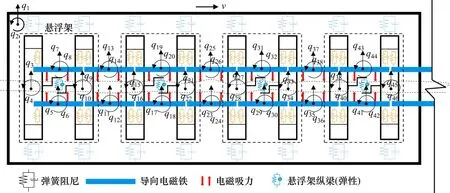
图3 尾车横向振动示意图Fig.3 Schematic diagram of the tail car lateral vibration

基于多刚体动力学，车辆振动方程可写为如式(1)的矩阵形式：

式中：qV={q1,q2,…,q246}T为广义自由度列向量；MV为车辆系统广义质量对角矩阵，其元素MVii为第i个广义自由度所对应的广义质量，平动自由度对应质量，摆头自由度对应转动惯量；CV为车辆系统广义阻尼矩阵；KV为车辆系统广义刚度矩阵；FV为车辆系统广义力列向量。

将车辆的弹簧阻尼系统编号，形成刚度元素对角矩阵KVD= Diag(k1,k2,…,k156)，采用矩阵组装法[8]可写出车辆广义刚度矩阵KV：

式中：KVtr为156×246 的刚度转换矩阵，其元素KVtrij表示当第j个广义坐标为单位位移时，其余广义坐标位移均为0 时，第i个刚度元素产生的单位广义刚度力。弹簧拉伸时刚度力为正，反之为负。

由于弹簧、阻尼成对出现，采用同样的方法，在式(2)中直接将KVD中的弹簧刚度系数替换为对应的阻尼系数，即可求得阻尼矩阵CV。

将电磁铁上的均布力简化为位于3 等分处的2个集中力，左右侧磁浮力编号奇偶不同以示区别，形成磁浮力列向量Fm={fm1fm2…fm156}T，并按式(3)建立广义力列向量FV：

式中：矩阵N为246×156的组装矩阵，其元素Nij表示第i个广义自由度为单位位移时，第j个磁浮力所做的功。当对应广义自由度i为侧移时，对应元素取值为1，对应广义自由度i为摆头时，其值取为磁浮力到电磁铁质心的力臂长度，正负号按磁浮力做功确定，当磁浮力j做正功时，元素Nij取正值，反之为负。

1.3 轨道梁振动方程

区别于中低速磁浮，高速磁浮列车在垂向和横向分别有独立的控制器进行悬浮、导向的控制，且由于轨道梁截面扭转刚度大，轨道梁扭转运动幅值小，因此，高速磁浮轨道梁垂向、横向振动是弱耦合的。

用40 跨长度为L的等截面简支梁模拟磁浮轨道梁，第k跨梁的强迫振动方程为：

式中：tki为第i个磁浮力进入第k跨轨道梁时间；xki为第i个磁浮力在第k个轨道梁上的位置；v为车速；H(t)为单位阶跃函数；δ(x)是Dirac 函数，具有挑选性质。

轨道梁以低阶模态振动为主，综合考虑计算精度与计算效率，基于模态叠加法取前6 阶模态，可满足精度要求并保证较高的计算效率，则第k跨简支梁的解可表示为：

式中：Tkj(t)为第k根轨道梁、第j阶模态对应的广义坐标；Yj(x)为简支梁模态函数，其表达式为Yj(x) = sin(jπx/L)。将式(6)代入式(4)，两边同乘模态函数Yj(x)，并沿梁长积分，并利用模态函数的正交性可得：

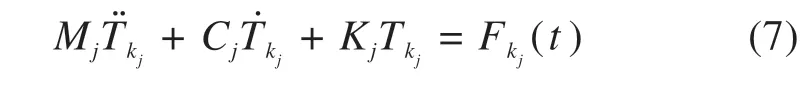
式中：Mj，Cj，Kj分别为与j阶模态对应的广义质量、广义阻尼和广义刚度，Fkj(t)为第k根梁的j阶广义力，k取1～40，j取1～6。

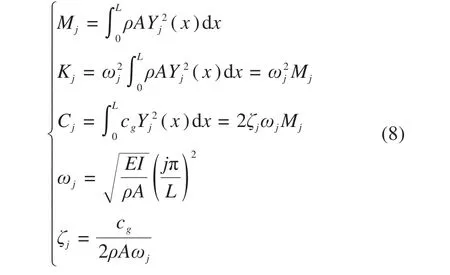
利用Dirac 函数挑选性质，在积分时消去x，并将模态函数表达式代入，得到广义力Fkj(t)：

1.4 电磁力控制方程

吴晗等[9]研究表明，当控制器时滞小于临界时滞时，系统处于稳定状态，本节假设时滞满足稳定性要求进行后续推导。磁浮力的自动控制模型如图4 所示，传感器采集磁浮间隙e(t)之后，由比例−微分(PD)控制器输出控制电压ur，再经运算放大器输出电压uc，使导向电磁铁上的线圈产生电流i(t)，进而产生电磁力以实现磁浮间隙控制。

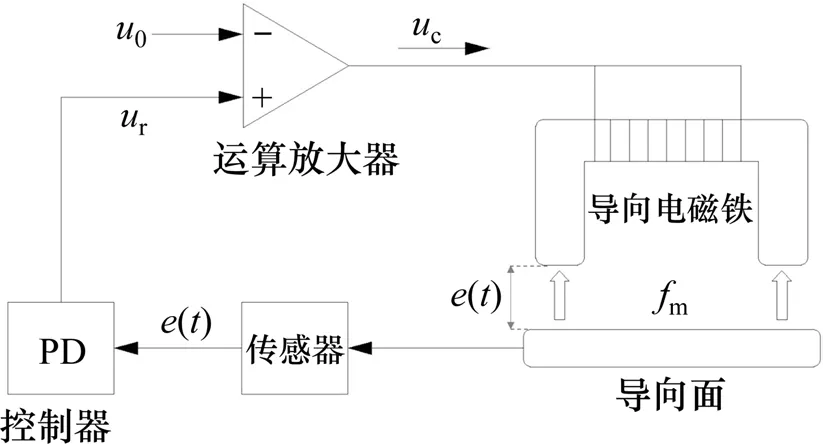
图4 磁浮力反馈控制示意图Fig.4 Schematic diagram of magnetic force feedback control

将电磁力fm在其平衡位置线性化表示[10]为电流i(t)与磁浮间隙e(t)的函数：

输出电压uc，控制电压ur及i(t)可按下式计算

式中：u0为预设电压；kp，kd分别为比例系数和微分控制系数。将式(11)代入式(10)，可得：

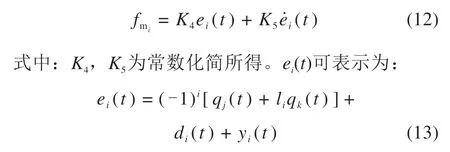
式中：qj(t)与qk(t)分别为第i个磁浮力对应的导向电磁铁的横移和摆头自由度的广义坐标；li为磁浮力至其所在电磁铁质心的距离，当对应电磁铁摆头运动使得i处产生与其侧移方向相同位移时取正，反之为负，yi(t)为轨道不平顺时域样本函数，按式(15)可得到。di(t)为第i个磁浮力所在位置处轨道梁横向位移，可表示为：

1.5 轨道不平顺模型

轨道不平顺是主要的外部激扰[2,11]，采用三角级数法进行时域反演得到方向不平顺样本xa(h)与轨距不平顺样本xg(h)，并依据几何关系得到左、右侧单轨不平顺时域样本函数yi(t)：

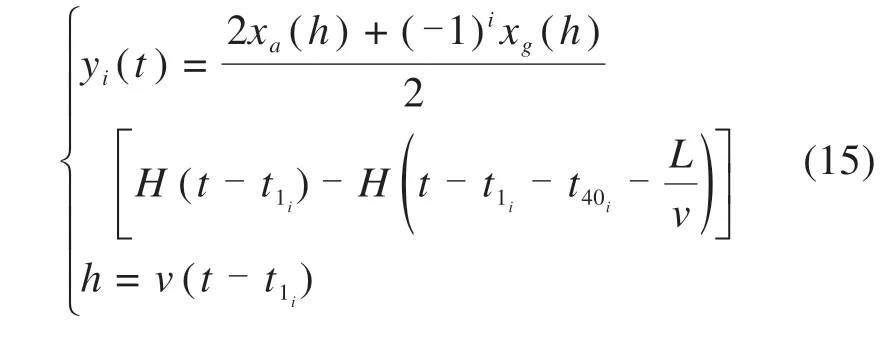
高速磁浮线路在不受载条件下测量的几何不平顺谱暂未见报道，但其导向面动态不平顺在10～100 m 范围内与高铁类似[12]，再考虑到磁浮力控制器低频跟随、高频抑制的特性[13]，故参考高铁不平顺谱并采用三角级数法进行时域反演，左、右轨不平顺时域曲线如图5如所示。

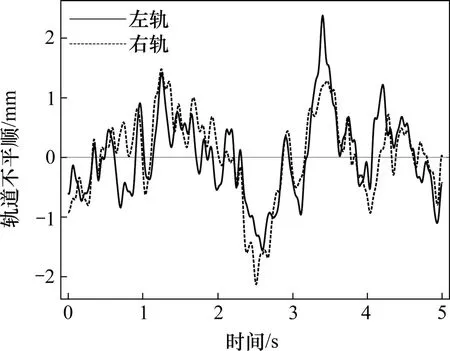
图5 轨道不平顺时域曲线(600 km/h)Fig.5 Time domain curve of track irregularities

1.6 车轨耦合系统方程及求解

由前文推导得到车辆振动微分方程组(1)，轨道梁振动微分方程组(7)和磁浮间隙代数方程组(13)构成指标为1 的车桥耦合振动微分−代数方程组，其中磁浮间隙代数方程为约束方程。引入状态变量zi(t)，方程组降阶为如下形式：

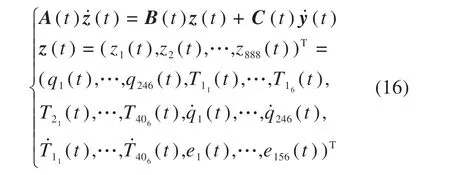
化为变系数微分方程组，本文使用Mathematica内置的隐式微分-代数方程求解器IDA进行求解[14]，得到耦合系统时域响应。值得一提的是，理论推导过程中关于广义自由度、弹簧阻尼系统及磁浮力数量均具有推广性。

2 算例分析

2.1 模型验证

为验证模型正确性，建立了轨道不平顺激励、时速600 km/h的耦合振动模型，并从以下4个方面对模拟结果进行考察：1) 根据控制要求，磁浮间隙应在其平衡位置±2 mm 范围内波动；2)由于PD控制器相较于PID控制缺少积分项，列车下桥后磁浮间隙应当产生一定的静差[15]；3)轨道梁振动应当完整反映出列车上桥—桥上运行—下桥的过程；4)与商业软件磁浮横向耦合振动结果对比。

图6为每节车首个磁浮间隙时程曲线图，由于轨道不平顺作用时轨道梁振动较小，轨道不平顺仍是磁浮间隙振动的决定性因素，因此各磁浮间隙曲线仅有微小区别，其最大幅值为1.8 mm，满足要求。在列车下桥后，磁浮间隙产生了小于0.5 mm的静差，满足PD控制的规律。

图6 每节车首个磁浮间隙时程曲线Fig.6 Time history curve of the first maglev gap of each train

图7为轨道梁跨中振动时程曲线，各跨梁在列车上桥后受到磁浮力激励振动，下桥后做有阻尼自由振动。邹逸鹏等[16]采用Simpack 建立较为精细的车辆振动模型对横向耦合振动进行了研究，重点关注磁浮车辆的动力响应，图8为本文与该文献结果的对比图，由于轨道不平顺在使用三角级数法进行时域反演时会在相位上引入随机函数，因此二者在相位分布上有所区别，但幅值近似，最大位移均为0.5 mm。

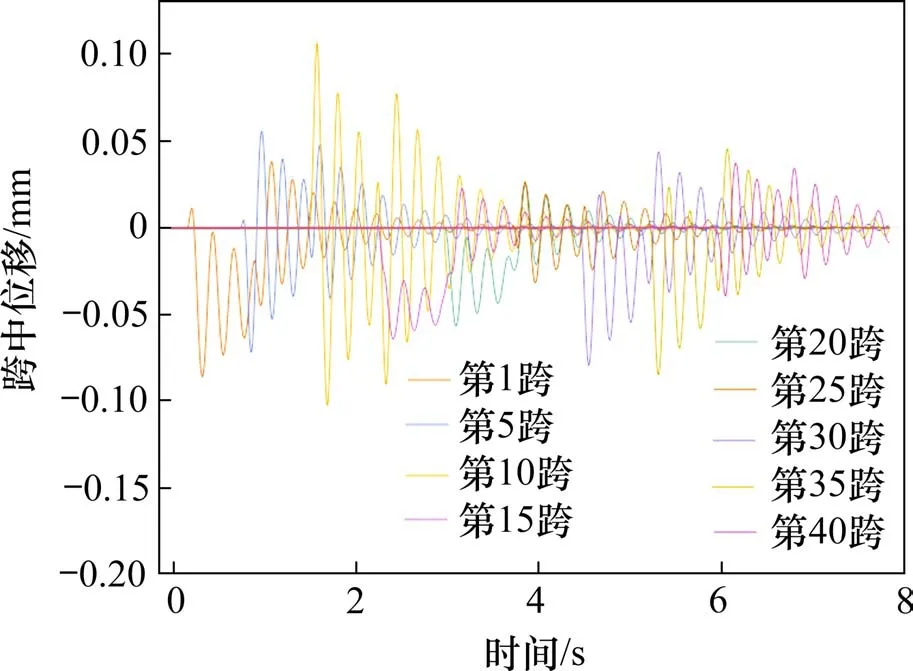
图7 轨道梁跨中位移时程曲线Fig.7 Guideway beam midspan displacement

图8 车体位移时程曲线对比Fig.8 Comparison of vehicle displacement time history curves

综上所述，数值模拟结果能够充分反映高速磁浮横向耦合振动的特征，符合磁浮系统耦合振动的宏观规律，车体位移幅值区间与其他研究结果相近。由此认为提出的耦合振动分析方法具有一定的参考价值。

2.2 风致横向荷载及轨道不平顺共同作用

磁浮列车气动力大小、作用位置等与列车外形等参数密切相关，毕海权等[17]通过数值模拟给出了5 列编组的TR 车型在20 m/s 连续侧风作用下的横向力，与本文模型所研究的列车属同一系列，故采用该文献给出的风致横向荷载幅值，研究系统的横向耦合振动。

图9 给出600 km/h 时磁浮系统的耦合振动响应，由图9(a)可知车体在横向荷载作用下偏离平衡位置，并在1.5 s 内达到新的平衡，之后在轨道不平顺激励下振动。图9(b)为磁浮间隙时程曲线，由于横向荷载作用，其整体向一侧偏移，最大波动幅值为2 mm。对于轨道梁，如图9(c)和图9(d)所示，相较于仅有轨道不平顺激励时其振动时程曲线产生了较为明显的变化，在列车上桥后各跨梁偏离平衡位置振动，并在列车下桥后振动逐渐衰减为0，其跨中最大位移为0.3 mm，最大加速度为0.12 m/s2。

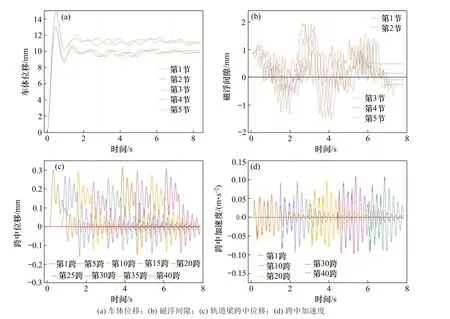
图9 横向荷载及不平顺作用下振动时程响应(600 km/h)Fig.9 Time history response of vibration under lateral load and track irregularity(600 km/h)

图10(a)给出跨中最大位移随行车速度变化的曲线。当车速为50～100 km/h 区间时，各跨梁的跨中最大位移处于0.20～0.21 mm 范围内，基本不变。而车速达到650 km/h 时，各梁的跨中最大位移则处于0.22～0.32 mm 之间，幅值增加且离散性加强。在《磁浮铁路技术标准(试行)》中规定允许跨中最大位移为1.98 mm，由图可知，侧风作用下各梁的最大位移均小于0.32 mm，远小于此值，表明在侧风荷载作用下新型轨道梁跨中最大位移满足要求；在各车速下跨中最大位移幅值在0.15～0.32 mm 范围内，未观察到剧烈的振幅增加现象，表明系统未产生共振。

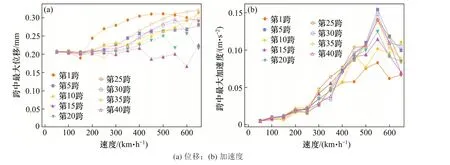
图10 不同速度下轨道梁跨中最大动力响应Fig.10 Maximum mid-span dynamic response of guideway beam at different speeds

图10(b)给出跨中最大加速度随速度变化的关系图，当车速为50～550 km/h 内时，最大加速度与车速正相关，最大值为0.15 m/s2。当车速超过550 km/h时跨中振动加速度最大值反而下降，这是由于车速提高，列车以更快的速度通过了轨道梁，当车速大于550 km/h 时，整车通过单跨梁用时小于1 s，作用于轨道梁之上的激振时间缩短，导致跨中最大加速度反而随速度增加而减小。

在风致横向荷载及轨道不平顺共同作用下，轨道梁跨中最大位移、最大加速度在各车速条件下均满足要求，系统未产生共振，表明新型轨道梁的横向动力学性能满足要求。