删失数据下含变量误差(EV)半参数变系数Panel模型经验似然

李文斌,何帮强

(安徽工程大学 数理与金融学院，安徽 芜湖 241000)

半参数变系数模型在近些年来被广泛研究的模型，它一般可以简化为线性模型部分、线性模型等一系列退化情形的模型。半参数变系数模型与其他线性或者部分线性模型相比较，是一种更应用多变的函数形式，同时还避免了相当多的“维数祸根”问题。研究考虑的是具有误差变量(Errors-in-Variables，EV)半参数变系数部分线性的模型：

(1)

式中，响应变量是Y;解释变量是X、Z和U,其中X是p维随机向量；Z是q维不可观测随机变量，U是1维随机变量；β=(β1,β2,…,βp)τ是p维未知参数量；g(U)=(g1(U),g2(U),…,gq(U))τ是q维未知函数向量;ε是不可观测的随机误差。

You等[1]研究了半参数变系数含EV的回归模型的估计，利用校正衰减方法提出修正的profile最小二乘法估计参数部分以及利用局部多项式的方法估计非参数部分。冯三营等[2]研究了半参数变系数模型，考虑其中的非参数部分的解释变量含有EV，并且构建了参数的局部的纠偏经验log似然比统计量。陈夏等[3]研究了半参数变系数部分线性EV模型，考虑的是参数部分解释变量具有EV。本文考虑的是模型的非参数部分的解释变量带有EV的半参数变系数面板数据模型。在医学、可靠性工程、金融保险、环境科学和临床的试验研究中经常会遇到随机删失的情况。王启华等[4-5]研究了随机删失的情况下半参数线性模型，考虑了其中的参数估计的渐进特征与参数的经验似然推断。陈放等[6]研究了在右删失的情况下，非线性回归模型的经验似然推断。侯文等[7]研究了在删失数据下，若干个半参数模型的经验似然和惩罚经验似然的推断。刘强等[8]研究了随机删失发生在响应变量中，部分线性EV模型的统计推断，考虑构建了其中的未知参数的经验log似然比统计量。李芸[9]分别研究了基于区间删失数据下的变系数模型和部分线性模型的统计推断。闫一冰等[10]研究了随机右删失发生在响应变量中，部分线性测量误差模型的统计推断。类似的研究还有许多，比如文献[11-18]都是最新的研究成果。面板数据在现今生活中应用非常广泛，比如经济、金融、生物、工程和社会科学等领域，同时面板数据可以为研究人员提供更大规模的扩展。在寻常的研究中收集的数据往往不能完全观测，面板数据更是由截面和时间序列融合在一起的数据，因此研究删失数据下的面板数据更具有实际意义。在删失数据下参数估计量的渐近方差会非常复杂，所以本文将经验似然应用其中，既不需要估计方差，又使得统计推断不会繁杂。因为有测量误差，所以研究对构造的辅助随机变量进行了修正，并修正了由测量误差引起的估计偏差。

本文研究了删失数据下含有EV的半参数变系数面板数据模型的经验似然推断，构建了关于未知参数的修正经验log似然比统计量，在合适的条件下证明了所构建的统计量趋近于χ2分布，所得到的结果可以用作构建未知参数的置信域。

1 方法与主要结果

假设数据{Yit,Xit,Zit,Uit,Wit,i=1,2,…,n;t=1,…,T}是来自{Y,X,Z,U,W}的一个独立同分布的样本，即有

(2)

式中，Zit是不可随意观测的随机变量；Wit是可观测到的随机变量；εit、eit是与Zit互相独立的，εit是随机误差，且E(εit)=0,E(eit)=0,var(εit)σ2<∞,var(eit)=Σe。

研究考虑的是删失下的情况，当响应变量Y被删失变量C随机右删失的时候，观察到的是ζit、δit，而不是Yit，其中，

ζit=min{Yit,Cit},δit=I(Yit≤Cit),i=1,2,…,n;t=1,2,…,T,

式中，Cit是来自删失变量C的样本数据，且假定{Yit,Xit,Zit,Tit,Wit}独立。假设A(·)、B(·)分别作为响应变量Yit与删失变量Cit的分布，记

τA=inf{u:A(u)=1},τB=inf{u:B(u)=1},

现假定

τB≥τA,Yit≥0,Cit≥0,i=1,2,…,n;t=1,2,…,T。

由于Yit被随机地删失，通常情况下参数的估计方法不能被直接的应用，原因是ζit与Yit拥有不一样的数学期望，需要对数据进行转换。当B已知时，定义

可以证明

采用Profile最小二乘估计的方法,假设有一个随机的样本{(Uit,Xit1,…,Xitp,Zit1,…,Zitq,Yit),i=1，…，n;t=1,…,T}来自于式(2)第一式。当β给定时，有

(3)

运用局部多项式的方法对模型(3)中g(U)这个变系数函数进行估计，假如操作中没有EV的情况，即Zit已知时，那么Uit在u0的一个小邻域内时，可以估计gj(Uit)为

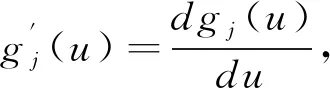
(4)

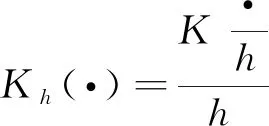
记

YB=(Y11B,…,Y1TB,…,YnTB)τ,X=(X11,…,X1T,…,XnT)τ,ε=(ε11,…,ε1T,…,εnT)τ,

W=(W11,…,W1T,…,WnT)τ,ωu=diga(Kh(U11-u),…,Kh(U1T-u),…,Kh(UnT-u)),

则基于式(4)由广义最小二乘法可得

(5)

因为Zit不可观测，可观测到的是含有误差扰动项WitW，如果式(5)中直接操作Zit被Wit替代，则这里的估计不再被认为是相合估计，为了消定估计中是EV所导致的偏差，参考了Feng等[19]的方法，对式(5)进行下面形式的局部修正得

(6)

这里的⊗表示的是克罗内克乘积。

定义S=(Q1W1,…,QnWn)，构建的辅助随机变量为

由于随机删失情况下的线性模型中参数估计量的趋近方差计算较为繁琐，运用近似于Owen[20]所提出的方法，可以得到经验log似然比函数为

然而，B分布函数在实际中往往未知，这时采用Kaplan-Meier估计

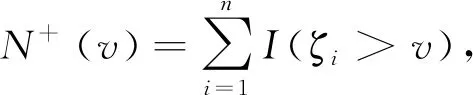
其中，

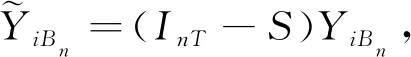
(7)

从而该参数的log经验似然比函数可以写为

(8)

由拉格朗日乘子法可得

(9)

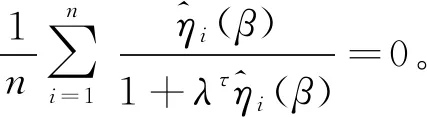
为了下面内容方便描述，引入一些记号，

A⊗2=AAτ,Φ(U)=E(WXτ|U),Γ(U)=E(WWτ|U),

Σ1(β)=E[(X-Φτ(U)Γ-1(U)Z)(ε-eτg(U))]⊗2-E[Φτ(U)Γ-1(U)ΣeΓ-1(U)Φτ(U)ετε]+

E{Φτ(U)Γ-1(U)(eeτ-Σe)g(U)}⊗2。

Δ=E(XXτ)-E(Eτ(WXτ|U)E-1(WWτ|U)Eτ(WXτ|U)),

Σ(β)=Σ1(β)-Σ2(β)。

为了得到研究的结果，列出下列条件，以下约定对任何向量a,用‖a‖表示Euclidean模。

A1：随机变量U具有有界支撑，其密度函数f(·)满足Lipschitz连续，且f(·)>0。

A2：{gj(·)，j=1,2,…,q}在U∈Ω内有二阶连续导数。

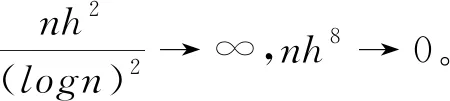
A5：存在常数s>2使得E‖X1‖2s<∞,E‖Z1‖2s<∞,E‖e1‖2s<∞,E‖ε1‖2s<∞,对某个δ<2-s-1，当n→∞时，有n2δ-1h→∞。

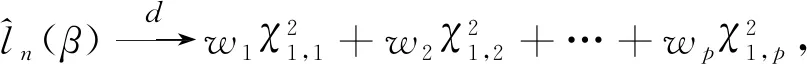
设An表示A的Kaplan-Meier估计，记

调整后的经验似然函数定义为

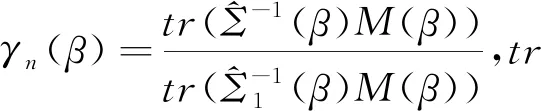
Iα(β)是参数向量β的置信域，这里的置信域是在具有趋近置信水平1-α的情况下,而且还有P(β∈Iα(β))=α+o(1)。

2 定理的证明

为了下文叙述方便，令

并且以下假设中c表示常数，在各处所取的取值不同。令

引理1 在条件A1～A5成立下，当n→∞时有

式中，j,j1,j2=1,2,…,q,Γj1j2(U)是矩阵Γ(U)的第(j1,j2)元素。

证明类似于文献[21]中引理A2的证明。

引理2 在条件A1～A5成立下，有

证明类似于文献[22]中引理A2的证明。

引理3 在条件A1～A5成立下，当n→∞时有

证明类似于文献[22]中引理A3的证明。

引理4 在条件A1～A5成立下，有

(10)

(11)

(12)

证明由泰勒展开，容易得到

首先证明，

由中心极限定理可得，

接下来可证

类似于侯文[7]的引理4.4的证明，可知

由以上证明可知式(10)成立。

类似于侯文[7]的引理4.7的证明，可得式(11)成立。

由引理1以及条件A5可得到

从而式(12)成立。

定理1的证明

然后由引理4得到

从而

再结合引理4，此定理可证。

定理2的证明：类似于文献[8]中定理2的证明可得。

3 结束语

近年来随着社会经济的迅猛发展，科研的不断深入，人们所收集到的面板数据越来越丰富，如何准确地处理和分析这些数据是目前统计学者们面临的一个大的研究课题。当半参数变系数部分线性EV模型应用在生存数据的分析时会面临一些困难，因为生存数据通常情况下都会是删失的。研究把经验似然方法推广到删失下带有EV的半参数变系数面板数据模型中，通过得到的统计量的趋近性质，说明了经验似然方法在删失下带有EV的半参数变系数面板数据模型中是有效的，为研究删失下带有EV的半参数变系数面板数据模型提供了一种方法与思路。