风沙两相流条件下凸条形态混凝土壁面冲蚀磨损研究
2022-03-30田菁艾陈善群
田菁艾,陈善群
(安徽工程大学 建筑工程学院,安徽 芜湖 241000)
西北部分地区是我国沙尘暴多发地区,位于该地区的构筑物长期暴露于恶劣的风沙环境下,常年受到沙尘颗粒的冲击和碰撞,其表面极容易出现冲蚀磨损的情况。工程中通常会采用改良强化材料或是在构筑物表面刷涂保护涂料的方法[1-3],以达到提高结构整体抗风沙作用的目的,并且一定程度上对结构表面起到保护作用。然而将多组强化后的材料进行对比后发现,仅仅考虑强化混凝土自身材料不足以说明材料在风沙作用中的抗冲蚀磨损能力,水泥基与骨料间接触面的粗糙度对抗冲蚀磨损性能具有较大程度的影响[4-5],从经济方面考虑,这两种方法都需要庞大的费用支撑。如何使构筑物自身在强风沙的环境中有更长久的寿命,已成为许多学者研究的方向,具有重要的现实意义和研究价值。
冲蚀现象是由多相流介质(通常为气固或液固)冲击材料表面后引发的一类磨损现象,在混凝土构筑物的磨损中属于较为常见的现象,多以材料的质量或体积损失量的大小来评估损伤程度。从十九世纪中后期至今,学者们结合理论分析、实验研究与数值模型的方法,对风沙的冲蚀行为作出了深入研究。混凝土材料是工程最常见的材料之一,学者们对其风沙两相流研究多集中于理论和实验:Finnie[6]、Goretta等[7]通过对比颗粒的大小形状从微观角度分析了冲蚀磨损现象的破坏机理;曹鑫、郝贠洪、张伟等[8-10]对金属、玻璃、陶瓷在风沙环境中的磨损状态进行了研究,并做出了细致的分析解释;王彦平、Masaya等[11-12]对混凝土材料的冲蚀特性进行了实验研究,考虑骨料在冲蚀磨损中的影响因素。同时,学者们也通过数值模型的研究方法对风沙耦合作用的运动进行了研究:Huang等[13]研究发现沙粒在风沙两相流中的运动也会在净风运动的过程中起到一定程度上的削弱作用;汤润超等[14]、方言[15]通过数值模型分别研究了沟槽、凹坑以及凸包等非光滑结构的抗冲蚀减阻性能;张卓群等[16]用数值模型模拟了杆塔结构,将沙粒假设成规则球体,求解出不同等级沙尘暴对输电铁塔的破坏作用,且均大于风荷载单独作用。目前对于混凝土材料的研究逐渐成熟,关于风沙对结构的冲蚀磨损主要通过改变输沙率表现,且以实验居多,设备仪器仍然具有一定的局限性,而沙的风选程度在研究中也不可忽视,需进一步修改和完善。如何在控制成本的同时提高混凝土壁面本身的抗冲蚀磨损能力,延长混凝土构筑物的耐久性能,非光滑表面形貌逐渐引起了许多研究人员的关注。
基于以上研究,本文借鉴其他领域抗冲蚀减阻的成功案例,针对混凝土表层结构的设计,拟建立一个适用于研究风沙两相流条件下凸条壁面冲蚀磨损且具有较高求解精度的数值模型。在验证模型可靠性之后,选择在表层布设单个半圆柱形凸条,优化混凝土壁面形态,以提高混凝土壁面抗冲蚀磨损的性能。在同一风沙环境下,通过改变风速和入射角度,将光滑壁面同凸条壁面的磨损情况进行比较,研究凸条结构对壁面的影响规律。同时,为了进一步发掘凸条对壁面抗冲蚀磨损的影响,本研究在不改变原有工况的基础上,采用双凸条的形式,以调整凸条间的距离的方式,系统分析间距对壁面冲刷的影响程度,可以为混凝土壁面抗冲蚀磨损研究提供有效信息参考,以期为沙漠地区的构筑物设计改善提供一种新的思路。
1 数值模型与验证
1.1 控制方程与模型选择
风沙流是沙粒在风的耦合作用下形成的流体,沙粒在风的推动作用下,其速度和压力会产生相应的变化,当变化达到一定程度时流体会发生湍流运动,从而导致建筑物表层出现不同程度的冲蚀磨损。本研究拟在笛卡尔坐标系中,通过求解雷诺时均Navior-Stokes(RANS)方程,结合RNGk-ε湍流模型计算以获取模型的风沙流场。以下为控制方程的形式。
(1)连续性方程:
(1)
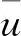
(2)
(3)
其中,
(4)

(2)湍流模型。湍流运动是一种常见的极其复杂的流动,选择合适的湍流模型对模拟风沙压力的准确性和模型收敛性具有重要的作用。研究选择RNGk-ε模型作为连续相模型,将满流分解成在时间上平均的运动与时刻上脉动的瞬间运动的合成,同时模型在标准k-ε模型的基础上对一些常数做出调整,将流体运动的瞬时参数值用时均值和脉动值的合成替代如式(5)所示:
(5)

(6)
方程组中,C1ε和C2ε为常量,这里为1.42和1.68;Gk与Gb表示为湍流动能,前者由层流速度梯度引发,后者由浮力作用产生;φi是湍流黏度;δk与δε分别是湍流动能k方程和湍流扩散ε方程的湍流Pr数的倒数,其计算过程如式(7)所示:
(7)
式中,δ0取值为1;δk和δε由实验获取,一般为1.393。
另外,为减少旋流作用对湍流模拟的影响,RNGk-ε模型在模拟计算中对湍流黏性做出调整,以修正该类影响,修正式如式(8)所示:
5.思想和行为变得早熟。受网络等媒体、社会、家庭等因素影响,学生在目标追求、思想意识、兴趣爱好、言行举止等方面出现多元化趋势,思想行为早熟。
(8)
式中,φt0是初始数值;Ω为旋流作用的特征数;as为常数,常规情况下取值0.05。
1.2 模型验证
为了验证所建模型的可靠性与精确度,选取王彦平等[11]所做的混凝土风沙实验作为参考依据,以边长为100 mm的C30混凝土立方体试块为参考对象,模拟试块表面在不同风速(19 m/s,23 m/s,26 m/s)下的冲蚀效果,同时改变风沙流的入射角度,30°~90°,期间以15°为间隔,对其冲蚀3 min,进口设置在距离试块200 mm的位置,以使前方近壁面流场可以得到充分的发展。为了保证风沙流出不对冲蚀过程和结果产生影响,故在模型壁面后方设置长1 000 mm的缓冲带。风沙流采用从左向右的流动方式,模型中流体选择连续相的理想空气为介质,裹挟以直径为0.25 mm的石英砂,颗粒沿进沙入口平行射入,进口位置定义流体的初始流速,设置边界条件为Velocity-inlet,出口处设置为Outflow,使其可以充分发展。
将数值计算试块光滑壁面受到冲蚀率结果与文献[11]原冲蚀实验数据进行对比分析,检验模型结果的准确性和可靠性,对比结果如图1所示。从图中两者的曲线可以看出,数值模拟计算的结果与文献中的结果虽然存在着差异,但是两者的结果走向呈现出较好的一致性。模型在模拟冲蚀的过程中,研究认为19 m/s的风速相对较小,选用理想空气为介质裹挟沙砾形成流体时,与现实中风沙流的气压有所区别,所以导致了结果上有些许偏差。
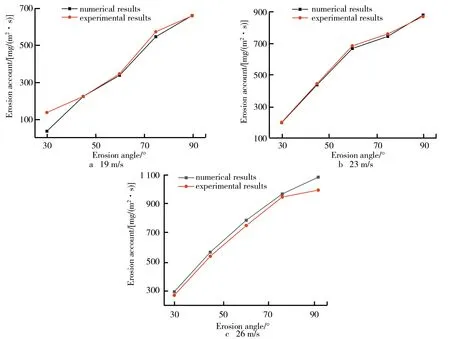
图1 不同风速下数模结果与实验结果对比图
1.3 计算域与参数设置
本研究建立了风沙两相流的三维数值模型的几何形式如图2所示。选取光滑和凸条混凝土壁面为研究对象,利用风沙入口喷射流体,实现建模过程。研究在建模时,为了保证所研究的两个壁面处于相同工况中,将光滑壁面与凸条壁面置于同一计算域中,以减小数模计算产生的误差,壁面尺寸设置为100 mm×100 mm,同时将两壁面的间距控制为600 mm,以防止两壁面间有流场干扰引起误差。在模型中壁面与进口处的距离为200 mm,同时根据不同工况的倾斜壁面角度,使其入射角度贴合工况要求,其倾斜角度0°~90°,以15°为间隔,模拟风沙流不同的入射角度,凸条设置为以6 mm为直径的半圆柱体,放置在凸条壁面中间位置。
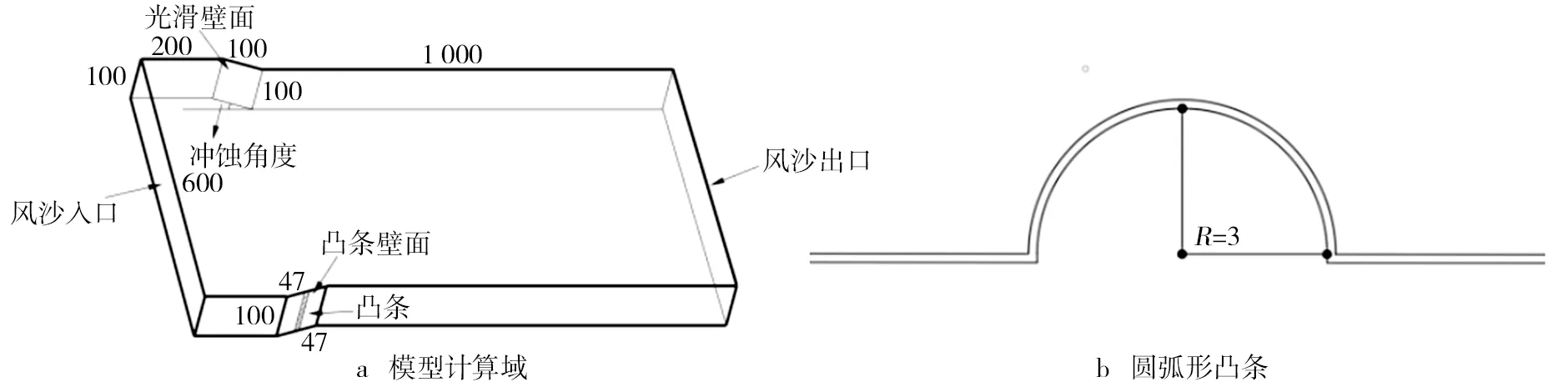
图2 模型计算域和圆弧形凸条示意图(单位:mm)
模型的外形是较规则结构,所以采用结构化网格划分。选择RNGk-ε湍流模型,结合DPM离散相模型进行数值计算。计算过程中选用SIMPLEC算法,空间离散格式设置为Second Order Upwind,设置亚松弛因子以控制模型中迭代变量的变化,其值如表1所示。

表1 亚松弛因子系数的设置
2 结果分析与讨论
本文对冲蚀磨损的研究主要集中在气固冲蚀方面,以气体为载体裹挟固体颗粒对构筑物表面进行冲蚀,并通过材料表面的质量损失量评估其损伤程度。对于混凝土冲蚀磨损影响因素的数模研究,需要确定合理的冲蚀程度衡量指标来精准衡量其磨损情况。研究对其冲蚀率结果进行采集和比较,分析与讨论壁面模型的冲蚀磨损程度。冲蚀率定义为单位面积上的质量损失,其公式为
(9)
式中,Rerosion为模型冲蚀速率;Nparticle为粒子总数;G(dp)为沙粒粒径函数;c(α)为撞击角函数;b(v)为速度指数函数;Sface为壁面表层面积。
2.1 风速对混凝土冲蚀磨损的影响
在其他参数设置不变的情况下,设置不同的风速,并将其冲蚀率结果对比分析。风向为30°入射角的混凝土壁面在19 m/s风速下的压力云图如图3所示。从图3中可以看到,凸条形态下壁面的压力主要集中于凸条前半部分区域,在凸条最高处位置受到压力值最小,该处受到风沙流的冲蚀磨损也相对较小。压力在凸条区域前方有较为明显的集中分布现象,表明粗糙砂砾在风的裹挟输送作用下,凸条壁面周围有明显的沙粒聚集,冲蚀磨损主要集中在凸条的前半部分,而凸条后方位置相对较好,笔者认为由于凸条的突出形态削弱了与其接触部分风的输送,减缓了部分沙粒的速度,使沙粒在凸条两边位置速度相对较小,之后随着风的继续裹挟输送其能量有所回增。不同风速下的凸条壁面冲蚀量如图4所示。从图4中可知,风沙流流速越大,流体的撞击动能越大,入射角度越大,流体对壁面持续冲蚀作用越明显。当入射角度较小时,风沙流对凸条壁面的冲击较为集中,流体的冲蚀磨损受切削影响较大;但当入射角度较大时,壁面受撞击影响较大,风沙流对凸条壁面的切削影响逐渐减小。

图3 30°壁面下凸条壁面压力云图(风速:19 m/s)

图4 不同风速下凸条壁面冲蚀量图
不同风速下凸条壁面和光滑壁面冲蚀情况的数值模拟结果如表2所示。在改变风速后,凸条壁面和光滑壁面的冲蚀速率有所改变,混凝土试件的冲蚀率随着风速的增大而增大。
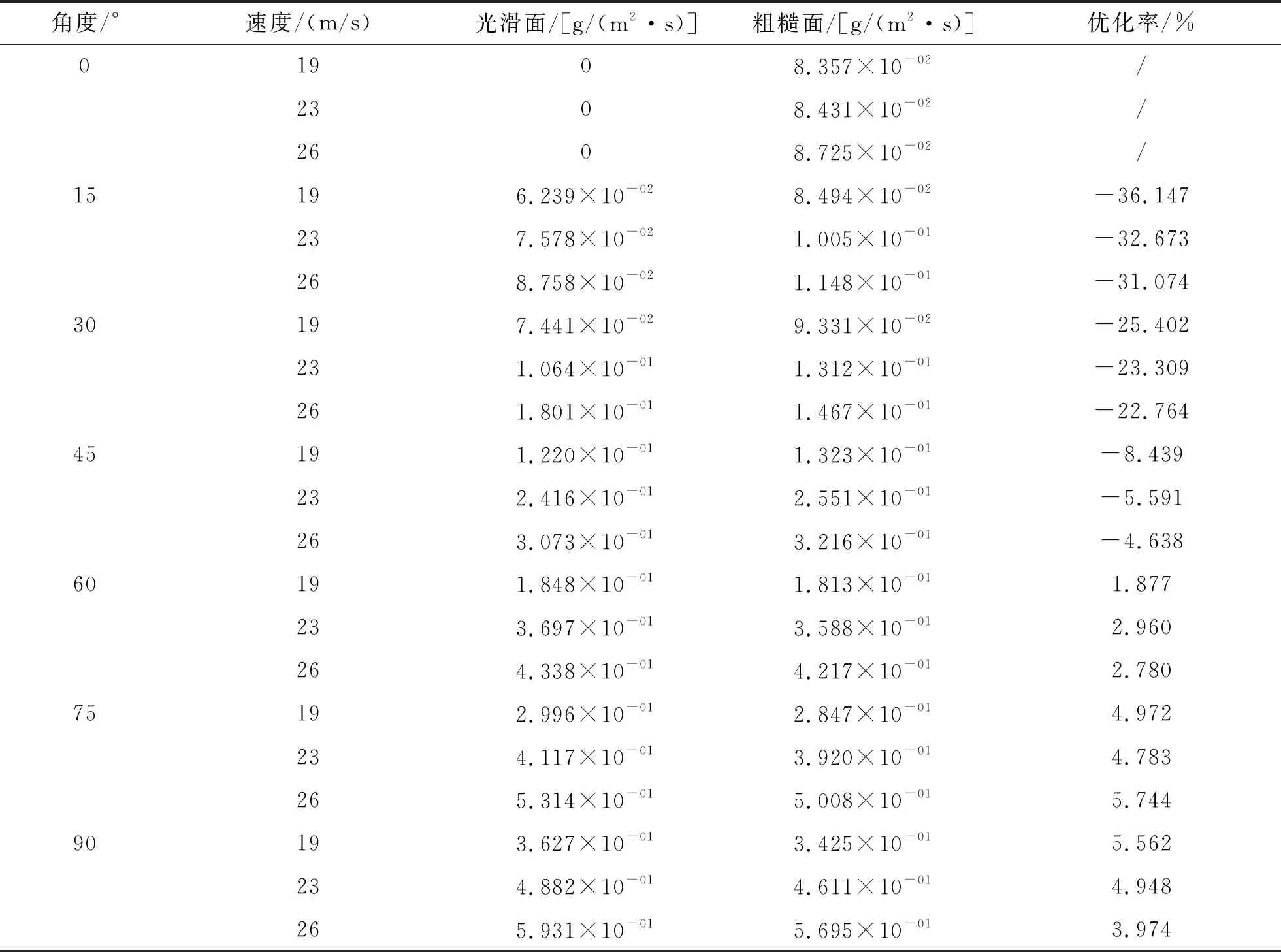
表2 不同风速下粗糙壁面和光滑壁面冲蚀量数值结果
在入射角与壁面成75°,风速为19 m/s时,光滑壁面冲蚀率为0.299 g/cm2,此时粗糙壁面冲蚀率为0.285 g/cm2,为光滑壁面冲蚀率的95%。而当风速为26 m/s时,光滑壁面冲蚀率为0.531 g/cm2,粗糙壁面冲蚀率为0.501 g/cm2,为光滑壁面的94.350%。由此可知,风速增大时,混凝土试件的壁面损失亦会随之增大。由表2可知,当风速为19 m/s时,结构优化表现出的效果最佳,甚至可以优化至5.562%,而当风速增大到26 m/s时,相同工况下模型的优化率为3.974%。分析其原因为:混凝土材料是一种脆性材料,在受到冲击作用时其破坏效果较为明显。当风速较小时,被裹挟的沙粒动能相对较小,对混凝土试件的冲击也较小,故而冲蚀程度较小;当风速增大时,沙粒的动能逐步增大,在碰撞混凝土试件时,沙粒给试件表面带来的破坏程度也随之增大,从而混凝土壁面的强度损失也更大。
2.2 入射角度对混凝土冲蚀磨损的影响
在其他参数设置不变的情况下,设置不同的风向,并将其冲蚀率结果进行对比分析。不同的入射角度在19 m/s的风速下光滑壁面和凸条壁面的冲蚀磨损结果对比如图5所示。从图5中可以看出,随着风沙入射角度的增大,混凝土冲蚀率显著增大,在30°入射角度以后冲蚀率有明显增加,且凸条壁面的抗冲蚀性能在高入射角度的情况下更为突出。当入射角度较低时,光滑壁面的冲蚀情况更为理想。在高入射角度(≥60°)条件下,凸条壁面迎风区域受到冲蚀磨损较为严重,相较于光滑壁面的冲蚀磨损优化效果并不明显,背风区域由于其凸出的壁面形态,部分流体有在此处回流的倾向,小部分风沙流在此处有小涡旋的产生,使得凸条周边的粒子冲击速度在流场的影响下有所减缓,部分流体经过漫反射撞击后与主流汇合,改变了下游风沙粒子的部分运动轨迹,减缓了粒子与壁面的碰撞频率,从而一定程度上降低了下游冲蚀程度。

图5 不同入射角下光滑面和凸条面的磨损情况对比(风速:19 m/s)
2.3 抗冲蚀磨损机理研究
沙粒在风的裹挟下对混凝土壁面产生的冲击作用是冲蚀磨损问题的主要来源。壁面受到来自沙粒入射的冲击时,产生的应力造成壁面表层脱落现象,可以将壁面受到沙粒作用产生的应力分解为与受力面垂直的法向正应力和与之平行的横向切应力,法向正应力对壁面的破坏由冲击作用主导,横向切应力对壁面的破坏主要为切削作用。当沙粒的入射角度较低时,与壁面间的冲蚀角度较小,此时更多受到横向微切削作用的影响,该影响对高硬度的混凝土材料来说较为轻微,沙粒的入射角度较高时,与壁面间的冲蚀角度较大,此时更多受到纵向冲击作用的影响,而混凝土材料自身韧性不高,其壁面表层脱落相对比较严重。沙粒分别经过光滑和凸条壁面(30°、60°、75°)的运动轨迹图如图6~8所示。图6~8中的α和β分别为凸条壁面沙粒入射角和光滑壁面沙粒入射角。当风沙流入射角度为30°时,凸条壁面的沙粒入射角度α30°明显大于光滑壁面的沙粒入射角度β30°,该情况下凸条壁面受到的冲击作用更大,冲蚀磨损情况更严重,光滑壁面的抗冲蚀磨损效果较好。当沙粒的入射角度为60°时,凸条壁面的沙粒入射角度α60°与光滑壁面的沙粒入射角度β60°在数值上是相近的,此时壁面受到的冲击作用大体上是相当的,光滑壁面与凸条壁面的冲蚀磨损程度较为一致。当沙粒的入射角度为75°时,凸条壁面的沙粒入射角度α75°明显小于光滑壁面的沙粒入射角度β75°,凸条壁面受到的横向切应力占主要作用,沙粒对壁面的破坏主要由微切削作用主导,而光滑壁面受到的垂直向正应力占比较大,更多的是受到沙粒的冲击作用,相比之下光滑壁面的冲蚀磨损情况则更为严重。
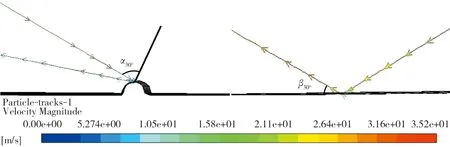
图6 30°冲蚀角度下凸条壁面(左)与光滑壁面(右)沙粒轨迹图

图7 60°冲蚀角度下凸条壁面(左)与光滑壁面(右)沙粒轨迹图

图8 75°冲蚀角度下凸条壁面(左)与光滑壁面(右)沙粒轨迹图
2.4 凸条间距对混凝土冲蚀磨损的影响
为了更深入地研究凸条布设对风沙流冲蚀磨损的过程影响,本研究在其他参数设置与算例相同的情况下,增设了一个相同直径的半圆柱形凸条,凸条并行放置于混凝土壁面中间位置并保持一定间距,其间距分别为1D、1.25D、1.5D、1.75D和2D,在19 m/s风速下不同壁面间距的磨损结果如表3~7所示。以便更直观地对比分析其优化效果。

表3 1D间距不同工况下粗糙壁面和光滑壁面冲蚀量数值结果
从优化结果可以看出,在增设了凸条以后,壁面的抗侵蚀性能有所提高。在双凸条的影响下,随着角度的增大,凸条壁面的优化率也有明显提升,其抗冲蚀性在高入射角度表现明显,60°冲蚀角时其抗冲蚀磨损性能大体上相当。虽然随着冲蚀角度的增大,光滑和双凸条壁面在风沙流的持续冲刷下其冲蚀磨损量是随之增大的,但是相比单凸条壁面时的磨损率,该值有较为明显的减小。值得注意的是,该优化效果在低冲蚀角度下趋势并不明显,仅在高冲蚀角度下起到一定的作用,这一结果与之前单凸条以及文献[16]中的影响结果相一致。沙粒对壁面的撞击为壁面质量损失的主要来源,壁面的不同形态会引起流体颗粒的冲击回弹现象。在低入射角时,沙粒对壁面凸条本身有强大的冲击力,造成壁面表层材料的脱落,且当撞击壁面回弹角度较大时,会对壁面形成二次撞击,加大了壁面的冲蚀磨损情况,使得壁面质量不断损失。在高冲蚀角度的情况下,流体对凸条壁面起到切削作用后低角度弹开,在其动能减小以后回归主流体中,同时少部分粒子在凸条后方低速运动形成漩涡流,对沙粒的撞击起到一定的阻碍作用,因此其抗冲蚀磨损能力有所提升。

表4 1.25D间距不同工况下粗糙壁面和光滑壁面冲蚀量数值结果

表5 1.5D间距不同工况下粗糙壁面和光滑壁面冲蚀量数值结果

表6 1.75D间距不同工况下粗糙壁面和光滑壁面冲蚀量数值结果

表7 2D间距不同工况下粗糙壁面和光滑壁面冲蚀量数值结果
19 m/s的风速下改变混凝土壁面凸条间的距离以后所得的数值模型结果如图9所示。从图9中可以看出,当流速保持一个相当的水平,随着入射角度的增大,凸条的冲蚀磨损也越大,且双凸条壁面的冲蚀磨损情况明显优于单凸条壁面,在高角度工况下,双凸条壁面的冲蚀磨损情况逐渐有所下降。凸条间距对凸条壁面的冲蚀磨损情况也有影响,随着凸条间的距离增加,其抗冲蚀磨损的能力也呈逐渐增强到减弱的过程。当凸条间距<1.5D时,双凸条壁面的冲蚀磨损值呈直线上升的趋势,而当凸条间距离≥1.5D时,曲线走向逐渐减缓。笔者认为在低冲蚀角度下光滑壁面流场中凸条间区域处涡旋作用微弱,颗粒在初次碰撞后迅速恢复,而双凸条壁面流场中的沙粒摄入壁面以后壁面承受水平应力的影响反弹,反弹粒子与主流粒子碰撞后迅速恢复,壁面受到冲击破坏;高冲蚀角度(>45°)下的凸条壁面抗冲蚀性能增强,粒子射入壁面后壁面承受垂直应力,随着入射角度的增大,凸条间区域的近壁面流场涡旋愈发成熟,削弱了该区域的沙粒动能,主流在其涡旋作用下发生向上的偏转,对凸条壁面的冲击效果有所减弱,从而提高了双凸条壁面抗冲蚀磨损的性能。60°时的1.5D双凸条壁面近壁面流场图如图10所示。由图10可以看出,位于两凸条后方形成的涡旋主要起到气垫作用,托动下方流体向着主流方向靠拢,减小壁面的直接冲击,从而减小壁面的质量损失,降低其冲蚀率。
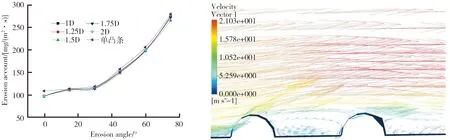
图9 不同间距下光滑壁面与凸条壁面的冲蚀磨损折线图(风速:19 m/s) 图10 入射角为60°时1.5D双凸条壁面近壁面流场图
3 结论
本研究采用了数值方法对风沙两相流条件下不同形态的混凝土壁面抗冲蚀磨损情况进行了研究。选用RNG k-ε湍流模型进行求解,对比分析了不同风速、入射角度下光滑和凸条壁面间数值结果的差异性。在此基础上,进一步研究了不同间距对凸条混凝土壁面的影响程度,可以得出以下结论:入射角度对混凝土壁面的冲蚀有明显影响,在冲蚀角度较低(<60°)时,凸条壁面的冲蚀率高于光滑壁面,其冲蚀分布有较为集中的现象,冲蚀磨损主要受冲击作用影响;而在高入射角度(≥60°)时,凸条壁面的抗冲蚀性能优于光滑壁面,其冲蚀分布散于整个壁面,冲蚀磨损主要受切削作用影响。风速对混凝土壁面冲蚀效果影响较大,随着风速的增加,风沙流的动能也逐渐增加,混凝土凸条壁面的冲蚀量随之增大,凸条壁面在60°角风向时优化效果最佳。当其他参数不变,调整混凝土壁面间的凸条间距时,其冲蚀磨损情况随着间距的增大而逐渐减小,相比单凸条混凝土壁面的抗冲蚀效果有明显提升,在入射角度较高且间距为1.5D时其总体抗冲蚀磨损性能较好。
