脉冲涡流TR探头解析模型的快速求解方法
2022-03-30李晓光孙加伟孔玉莹朱悦铭程婧婷王海涛
张 卿,李晓光,孙加伟,孔玉莹,朱悦铭,程婧婷,王海涛
(1.南京航空航天大学 自动化学院,南京 211100;2.中广核检测技术有限公司,江苏 苏州 215000)
0 引言
金属材料如铝、不锈钢、碳钢等在核电设备、石油化工设备等广泛应用。这些材料在使用过程中,由于恶劣现场环境或电化学作用等会在材料内部形成局部大面积腐蚀[1],当腐蚀达到一定程度时,可能会突然故障或爆裂,引发事故。因此,对这些材料进行定期检测对于保证设备的安全运行具有重要意义。现有的检测方法主要包括超声检测、射线检测和涡流检测方法等。超声检测可对设备表面和内部缺陷进行检测,然而其需要耦合剂[2],打磨被测件表面不光滑的部分,增加成本的同时又使检测工序繁琐化;对于射线检测方法[3],其相比超声检测工序更简单,无需打磨,但是依然有检测速度慢的问题,并且检测具有辐射风险,对安全防护要求非常高,操作不便;涡流检测操作方便,可以在不接触被测件的条件下进行检测,但是由于趋肤效应的影响,涡流集中在进表面区域,因此该方法不适于内部缺陷检测,只能检测被测件表面[4]。脉冲涡流检测(PECT,pulsed eddy current testing)技术作为涡流检测的新型分支,以阶跃信号作为激励,利用其频谱宽的特点,对被测件表面及近表面缺陷进行检测,避免了传统涡流检测技术的局限[5]。因此,脉冲涡流在设备内部缺陷的检测中有良好的应用前景。
近年来,脉冲涡流检测技术越来越广泛的被用于设备的内部腐蚀检测,围绕其展开的研究也越来越多。为了更好的理解脉冲涡流的检测机理,同时对现场设备检测的结果进行预测,研究人员一般会将实际检测中遇到的问题进行化简建模,并基于电磁理论分析求解模型。按照分析方法分类,脉冲涡流检测模型可分为两种,即“解析模型”和“数值模型”[6]。解析模型作为以闭式解为结果的模型,表征了检测信号与检测参数关系,在能够实现高精度且快速的计算,具有明确物理意义,因此在脉冲涡流检测中得到了广泛应用。
关于脉冲涡流解析模型的研究,20世纪50年代Waidelich[7]建立了脉冲涡流模型,针对双层导电材料,假设了被激励线圈所激发的为平面电磁波,推导了时域解析解。然而,Mottl[8]研究表明能够激发出平面电磁波的前提是激励线圈足够大或者被测件厚度无限大,因此在实际检测中Waidelich所建立的模型具有低精度和大误差的弊端。20世纪60年代,Dodd和Deeds[10]结合了分离变量法和麦克斯韦方程组推导了放置式线圈位于两层半无限大导电材料平板上方的解析解。随后,Cheng[11]针对Dodd-Deeds模型中计算繁琐的系数矩阵提出了传递矩阵法;Theodoulidis[12-13]引入了截断区域特征函数展开法(TREE法,truncated region eigenfunction expansion),以无穷级数代替了Dodd-Deeds模型中的积分表达式,简化了模型的求解过程,提高了计算效率。上述方法为后续脉冲涡流解析模型的研究奠定了基础。
近年来,随着脉冲涡流技术的日益广泛应用,需要解决的问题越来越多,对模型的多样性及精度要求也越来越高。比如,由于阵列探头的广泛应用,对其阵列单元——即激励和接收线圈非同轴的Transmitter-Receiver阵列单元(以下简称TR探头)的解析分析需求迫切。Rybachuk[14]等和Yin等[15]基于极坐标变化方法建立了关于TR探头的二维解析模型,计算了矩形激励线圈和圆环形截接收线圈的阻抗。随后,Cao[16]等求解了矩形线圈作为接收线圈的模型并得到了含角度的双重积分的线圈表达式。本课题组的Zhang[17]利用第一中值积分定理,求解了含角度双重积分的线圈阻抗表达式,获取了形式简单的解析解。然而,上述模型均将构件局部大面积腐蚀缺陷等效为均匀壁厚减薄缺陷,精度较差。为提高模型建模精度,Theodoulidis求解了非铁磁平板导体中含槽型缺陷[18]和通孔缺陷[19]的解析模型,分析了线圈阻抗随缺陷深度和宽度变化的关系。本课题组的张卿[20]推导了铁磁材料中含有平底盲孔试件的模型,进一步拓宽了模型的适用范围。然而,上述模型所用探头为同轴式探头。针对TR探头,含平底盲孔构件的解析模型还未得到研究。
基于此,本文在上述研究基础上,对TR探头检测含平底盲孔构件的脉冲涡流解析模型展开研究,并给出了一种快速求解该模型的方法:首先,建立含平底盲孔构件脉冲涡流TR探头解析模型,并分析其求解过程;然后,参考已有的TR探头模型和含平底盲孔构件同轴式探头检测模型,分别获取线圈系数和广义反射系数,进而得到含平底盲孔构件脉冲涡流TR探头模型的解析解;最后,用实验验证上述解析模型的正确性。
1 模型求解方法分析
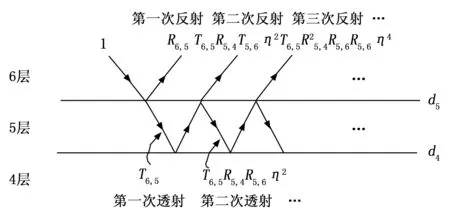
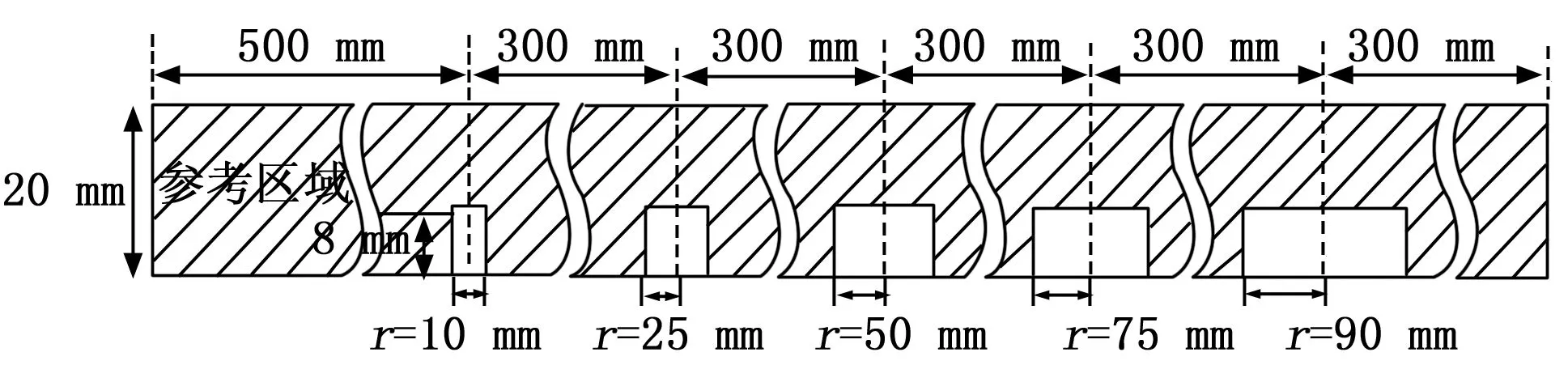
核电设备或石化管道中的设备通常分为很多层,考虑到石化行业中的设备每层材料不同且更为复杂,因此本文参考石化行业的带包覆层管道,建立如图1所示的含平底盲孔构件脉冲涡流TR探头解析模型。其中,第1层到第6层分别为:空气、管道内壁、管道外壁、外包覆绝缘层、最外保护层及空气。在第6层中,TR探头置于此,同时将该层分为3部分:I、I-II和II。另外,由于介质电磁属性在z方向属性不同,平底孔构件被分为第2层和第3层两层。其中第3层为材料及壁厚均匀构件,第2层为包含深度(d1-d2)、半径c的平底孔。而在第2层中,其又被平底孔划分为两个子区域,0≤r≤c为空气区域,c 图1 非同轴式激励和接收线圈置于平底盲孔构件上方 根据傅里叶变换,方波激励可看作一系列谐波激励的叠加,因此可先求解各谐波的感应电压,然后利用傅里叶逆变换,得到脉冲涡流的时域感应电压信号。根据Dodd-Deeds模型,谐波激励下,接收线圈感应电压解的形式可表示为: (1) 其中:j为虚数单位,ω为谐波的角频率,I为谐波电流的幅值,μ0为真空磁导率;l1为提离,e-2αl1为提离系数;S(α)为线圈系数,R′(α)为广义反射系数。e-2αl1、S(α)、R′(α)三者相互独立,且S(α)仅与探头结构和参数有关,R′(α)仅与试件结构相关,e-2αl1仅与探头提离有关。 事实上,由于线圈系数、广义反射系数和提离系数三者相互独立,因此对于任意脉冲涡流检测模型,谐波激励下线圈的响应均可以表示为式(1)所示的形式,且R′(α)仅与所求解模型的构件有关、S(α)仅与探头有关。同理,如果已经获取了其他模型的线圈系数和广义反射系数,则相同探头的线圈系数是相同的;如果相同试件的广义反射系数也是相同的,则这些线圈系数和广义反射系数不需要再重新计算,只要将其组合即可得到新模型的解析解。 基于上述分析,图1所示的复杂模型可简化为图2所示的两种较为简单模型的组合。其中,如图2(a)所示模型为保持探头为同轴探头不变,试件为含平地盲孔的试件。根据上文中的分析,图2(a)所示模型的广义反射系R′(α)与本文要求解的含平底盲孔构件脉冲涡流TR探头解析模型的广义反射系数R′(α)相同;同样,图2(b)所示的为均匀减薄构件TR探头解析模型。由于图2(b)所示模型和图1所示模型的探头结构完全相同,则根据上述分析,图1所示模型解析解中的线圈系数应和图2(b)所示模型的线圈系数一致。则通过图2(a)和图2(b)分别可获取R′(α)和S(α),将其带入式(1),即可求解平底盲孔构件TR探头检测模型的解析解。 图2 模型的简化 根据第一章给出的思路,求解含平底盲孔构件脉冲涡流TR探头模型的解析解。其中,如图2(a)所示的平底盲孔构件同轴式探头模型已经在文献[20]中得到了研究,因此通过文献[20]可获取广义反射系数。同样,如图2(b)所示的均匀减薄构件TR探头解析模型已经在文献[17]中得到推导,因此线圈系数S(α)可通过文献[17]获取。 广义反射系数实质上是反应激励线圈激发的电磁波在多层试件中传播和衰减规律的系数。如图3给出了电磁波在图1所示多层结构中的第4层到第6层的传播过程示意图,其中:第一次反射R6,5和第一次透射T6,5发生在第6层和第5层分界处,又因为介质厚度有限,在第5层的底面处,第一次透射波发生了多次反射和投射,同时一部分进入第6层,因此在第6层中出现了第二次反射波T6,5R5,4T5,6η2、第n次反射波T6,5R(n-1)5,4R(n-2)5,6T5,6η2(n-1)…其中,η=e-β5(d4-d5)。广义反射系数的含义为第6层中的所有反射波的幅值和相位和与入射波的比值。 图3 电磁波在分层介质中的传播 文献[20]已经根据Dodd-Deeds模型和Cheng的传递矩阵法详细的给出了图2(a)所示模型的广义反射系数推导过程,其求解的一般思路为:根据麦克斯韦方程组构造图2(a)所示模型各层的磁矢位A的表达式: DkY1(αr)]dα (2) 其中:k为层数,J1(αr)和Y1(αr)分别为第一类和第二类贝塞尔函数,μrk和σk分别为第k层的磁导率和电导率,Ck、Bk、Dk为第k层的系数,广义反射系数的表达式主要与系数Ck、Bk、Dk有关。 根据z方向和r方向的边界条件求解系数Ck、Bk、Dk,并为简化求解过程,根据文献[7]将其写成矩阵形式: (3) 最后,根据式(4)所示的传递矩阵中系数Ck、Bk与广义反射系数的关系求解广义反射系数,结果如式(5)所示: (4) (5) (6) (7) (8) (9) 线圈系数反应的是线圈结构对检测结果的影响,其对于线圈设计和现场应用中线圈的选择具有重要指导意义。文献[17]已经推导了当探头结构为TR探头时,线圈系数的表达式,其一般的思路为:首先,获取图4所示接收线圈为单匝线圈时,线圈系数的表达式;其次,利用叠加原理得到接收线圈为矩形截面线圈时,线圈系数的表达式,此时得到的表达式中包含与线圈角度相关的积分IntR,如式(9)所示,因此不便于用于线圈设计和分析。然后,文献[17]通过两次应用第一积分中值定理简化了式(9),并最终得到了图2(b)所示TR探头的线圈系数,结果如式(10)所示。 图4 单匝接收线圈的TR传感器 (x[(df+cosθ)2+(sinθ)2]1/2)dxdθ (9) (10) (11) 其中:J0(αr)为0阶第一类贝塞尔函数;(l2-l1)为接收线圈高度,r1和r2分别表示线圈的内、外半径,n是线圈匝数;下标T表示激励线圈,R表示接收线圈。 同样,由于图1所示模型的探头与图2(b)所示模型的探头完全相同,因此,式(10)同样也为图1所示模型的线圈系数。 根据上述分析,图1所示的含平底盲孔构件脉冲涡流TR探头模型的解析解可通过将TR探头对S(α)的影响和平底盲孔构件对广义反射系数的影响组合得到,则平底盲孔构件TR探头检测模型的解析解为: (12) 此外,对于激励电流为方波的情况,将通过式(9)计算得到的各谐波感应电压相加,并对结果作离散傅里叶逆变换,可得到脉冲涡流的时域感应电压信号: (13) 其中:m表示第m个谐波,N表示采样点数。 为针对基于TR探头的平底孔构件缺陷检测,验证解析模型正确性,将其用于16 MnR平底盲孔构件检测并对实验结果进行分析,实验系统及各部件关系如图5:激励方波信号由信号发生器产生,经由功率放大器放大后形成稳定的激励电流加载到探头激励线圈中;其次,由于变化的电流在试件中激发出涡流场,接收线圈即可将捕捉到的而此次长转化为电压信号,通过前置放大器后由数据采集卡转为数字信号传输至计算机进行数据显示和保存;最后,通过计算机中的算法保留与构件有关的信号信息,继而得到感应电压信号ΔU。在此实验中,检测对象为16 MnR的平底盲孔构件,如图6示,构件厚度为20 mm即(d3-d1),其中平底盲孔深度(d2-d1)为8 mm,半径大小如图所示(本文仅选用r=90 mm的平底盲孔进行解析模型验证)。另外,在此构件中也包含用于参考对比的无平底孔区域,即图6中的参考区域。在构件平底盲孔上采用厚度40 mm的塑料板模拟绝缘层,绝缘层上方则采用厚度0.5 mm的白铁皮模拟保护层。实验所用到的探头参数如表1所示,方波激励电流的幅度,占空比和周期分别设置为4 A,50%和1 s。 图5 脉冲涡流检测系统功能示意图 图6 平底盲孔构件示意图 mm 表2 材料参数 在与上述研究参数保持一致的前提下,借助Matlab软件计算公式(13)所示的模型解析解。在构件的无平底盲孔区域以及半径为90 mm的平底盲孔区域进行实验与计算得到对应感应电压曲线如图7所示。其中,TR探头激励线圈与接收线圈的轴心间距离D为150 mm,同时,为了突出信号间的差异,图中以双对数坐标系进行展示。由图可知,感应电压信号经过归一化处理后与实验曲线及计算曲线基本吻合,验证了基于TR探头的平底孔构件缺陷检测模型的正确性。 图7 实验和计算感应电压信号比较 本文求解了平底盲孔构件TR探头检测解析模型。以解析解的特点为参考依据,在对模型进行求解时针对广义反射系数受平底盲孔的影响及S(α)受探头结构的影响进行研究,将求解过程简化。对于16MnR平底盲孔构件,应用上述模型通过实验进行验证,并将所得实验结果与解析模型解进行对比,所得结果基本吻合,解析模型正确性得到验证。基于TR探头的平地盲孔脉冲涡流检测解析模型,在更多脉冲涡流检测问题上都能提供理论指导,极具工程意义,接下来的工作研究内容将围绕该模型在脉冲涡流检测中的应用展开。

2 模型求解
2.1 获取广义反射系数







2.2 获取线圈系数


2.3 平底盲孔构件解析解

3 实验结果与讨论




4 结束语
