一种光学卫星无控定位误差智能建模方法

陈 昊,乔 凯,刘伟玲

(1.北京跟踪与通信技术研究所，北京 100094; 2.武汉大学 测绘遥感信息工程国家重点实验室，武汉 430000)

0 引言

长期以来，世界各国竞相发展航天遥感技术，陆续发射了系列对地观测光学卫星，如美国的GeoEye、WorldView系列卫星，法国的SPOT、Pleiades系列卫星等。国外依靠硬件优势，结合地面定标、误差建模等高精度处理技术，实现了光学卫星全球最高3～5 m的无控定位精度[1-5]。“十二五”以来，我国在高分辨率对地观测卫星领域均取得重大成果，至“十三五”结束，我国高分专项卫星完成部署，民用领域光学卫星最高分辨率已可达0.5 m左右。虽然国内光学卫星影像分辨率日益趋近国外先进水平，但国内光学影像无控精度普遍在10米开外，与国外仍有较大差距。

已有研究表明，影响光学卫星无控定位精度的因素包括姿态测量精度、结构变形等引起的低频姿态误差。国内相关单位针对上述两方面开展了大量研究。针对姿态测量精度，2012年发射的资源三号01星，姿态测量精度/频率可达到3″/4 Hz[6-8]，2014年发射的高分二号卫星姿态确定精度可达3.6″，2019年发射的高分七号卫星姿态确定精度可达到1″，姿态测量误差得到很好的控制[9]；而针对低频姿态误差，熊凯等采用扩维卡尔曼滤波方法，将卫星成像姿态、低频误差参数作为变量进行同时估计，并在真实卫星遥测数据的基础上构建了仿真模型，利用仿真数据对所提方法开展验证，结果表明该方法在低频误差较大情况下的效果明显优于低频误差较小情况，其中当低频误差较小情况的姿态确定精度甚至不如传统的扩展卡尔曼滤波方法[10]；Lai Yuwang等学者首先对STECE(空间技术试验和气候探测)卫星两颗星敏间的夹角变化进行频谱分析，该研究认为星敏夹角变化可以侧面反映因外热流引起的结构变形，最终造成姿态低频误差。通过采用Vondrak滤波算法可以抑制该误差对姿态确定的影响，使滤波后的姿态低频误差峰值相交补偿前更小[11-12]。

国内部分学者试图从地面处理的角度出发，直接建立无控定位精度随成像参数的变化规律，以求对定位误差进行预测补偿。王艳丽等学者认为姿态低频误差主要由外热流引起的结构变化造成，且该变化与太阳高度角相关，进而提出一种顾及太阳高度角变化的光学影像姿态低频误差标校与补偿方法，建立了姿态低频误差的傅里叶级数展开模型，并利用地面控制求解模型参数，将海洋1C卫星无控定位精度从3.8像元提升到1个像元[13]；管志超等学者同样认为姿态低频误差与外热流引起的结构变形紧密相关，该变形可能与成像星下点经纬度存在关系，建立了无控定位误差与成像星下点经纬度的关系模型，并利用资源三号卫星正视相机开展了验证，建模精度可在10米以内[14]。

但是，姿态低频误差的产生原因是多方面的，包括星敏/星相机内部随温度变化、外热流引起的结构变化等，因素多，难建模，传统通过地面控制点结合经验模型的建模补偿方法难以客观、全面的揭示姿态低频误差的特征规律。本文提出了一种光学卫星无控定位误差智能建模方法。首先，基于卷积神经网络对无控定位精度建模；其次，以卫星成像参数和业务系统全自动几何质检结果作为学习样本，利用网络训练无控定位精度与成像参数的关系，挖掘无控定位误差规律；最后，通过预测定位误差来提升无控定位精度。

1 算法原理

卫星在轨运行中，通常采用GPS设备测量其相位中心在WGS84坐标系下的位置及速度矢量；星敏及陀螺等定姿设备测量卫星成像姿态：当星敏参与定姿时，利用观测数据最终确定卫星本体相对于J2000坐标系的姿态；而当星敏不参与定姿时，则通常测量卫星本体相对于轨道坐标系的姿态。当前国内在轨的线阵推扫卫星均采用了星敏定姿，因此本文研究几何定位模型中仅考虑J2000坐标系下的姿态测量数据。

相机随着卫星的运动而推扫成像，各行影像符合中心投影原理。依据相关坐标系定义及转换，可构建线阵推扫光学卫星几何定位模型如下[15-16]：

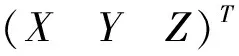
根据几何定位模型，成像误差源梳理如表1所示。

表1 误差源梳理

表1中，“”标示误差通常可以通过常态化在轨几何定标进行消除，“”代表难以通过定标消除的在轨误差。可见，影响无控定位精度的主要误差源来自于姿态低漂、姿态随机误差、时间随机误差。目前已有研究种，部分学者认为姿态低漂主要由外热流引起的结构变形造成，其可能与成像星下点经纬度或太阳高度角有关；而姿态随机误差则认为主要由星点识别误差造成，与星敏/星相机状态、成像空间等相关。由于误差产生机理复杂、误差源多且难以解耦，传统方法难以建立无控几何定位精度的变化规律模型。因此，为更为全面、客观地建立无控定位误差随姿态低频误差、测姿随机误差等的变化规律，本文搭建深度学习框架，以成像参数、无控定位误差作为训练对，通过模型训练，实现对给定成像参数的无控定位误差预测，进而提升无控定位精度。本文技术流程如图1所示。

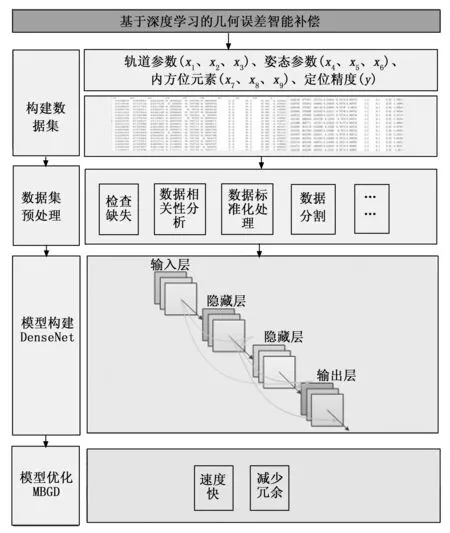
图1 光学卫星无控定位误差智能建模处理流程

1.1 构建光学无控定位误差模型数据集

无控定位误差本质上是由测姿随机误差、低频误差等引起。而测姿随机误差主要与星敏/星相机状态(如因温度变化造成的焦面变化)、成像空间(即观测恒星的星等、数量等情况)相关，而低频误差与外热流等相关，而无论温度变化、成像空间变化或者外热流等，均可包含在卫星成像的相关参数种，例如星下点经纬度、成像姿态。因此，可以利用无控定位误差与成像参数作为训练对来搭建样本集。

当前卫星业务处理系统均包含自动几何质检模块，可以利用国内外公开的较高精度几何基准数据开展几何质检，评估得到每景影像的无控定位误差。为了进行无控定位误差智能建模，文中对影响卫星定位精度的核心要素进行筛选，例如可选取影响卫星定位精度的星下点位置、成像姿态等作为模型回归拟合的自变量，相应的定位误差作为回归拟合的因变量[18-19]：

Y=f⊙(Xroll,Xpitch,Xyaw,Xlat,Xlon)

(1)

式中，xroll，xpitch，xyaw分别为影像拍摄时的成像角度，xlat和xlon分别为星下点经纬度，⊙为神经网络运算。

1.2 数据预处理

卫星成像数据传输过程，可能存在误码等现象，造成少量影像数据无控定位异常，该部分数据不应加入样本集进行训练。因此，在构建数据集中，我们首先需要对样本进行预处理，以提高模型预测精度。

1)我们利用Pandas库提供的drop函数接口和isna函数接口，对初始样本集种的所有样本进行数值探测，剔除数值过大或者过小的异常值，避免影响模型拟合精度。

2)采用Pandas库提供的corrwith函数，对选择的自变量和因变量进行相关性分析，若因变量与自变量相关性强，则说明该自变量因素是引起无控定位误差变化的主要因素，若相关性弱，则该自变量因素可能与无控定位误差变化无关。设定corrwith函数阈值为0.000 1，剔除相关性小于0.000 1的自变量因素。

3)由于数据在数量级上存在较大差距，易造成模型陷入局部最优状态，我们采用标准化方法对样本集进行处理。在文中总共采用了3个函数进行标准化处理，分别是MinMaxScaler、Normalizer、StandardScaler。经过反复验证和调整参数，最终采用的标准话函数是MinMaxScaler。最终获取文中数据集。

1.3 DenseNet模型构建

深度学习可以通过构建具有多隐藏层的神经元节点来构建机器学习模型，并从海量的数据中学习隐藏的特征，以实现对数据的高准确性预测。深度学习之所以称之为深度学习是因为它相较于浅层神经网络模型具有更多的层，并且它的优势是可以实现特征的自动学习，与传统方法相比，它能挖掘更深层次的数据特征。

卷积神经网络(CNN，convolutional neural networks)模型是深度学习中最具代表性的模型之一，在计算机视觉领域有着广泛的应用，但随着应用领域的不断扩展，CNN模型在随着网络层数不断加深时，神经网络层的梯度消失问题逐渐显现，这一问题也导致了CNN个学者对该问题的改进。DenseNet通过将所有层直接相互连接，在实验过程中也验证了该操作可以有效减轻梯度消失的问题。文中也借鉴了DenseNet网络的优势[15]，构建适用于珞珈数据的神经网络模型。DenseNet网络通过将每一层中的神经元以前馈的方式与其他层均进连接，每一层的输出都是前面所有层的输入经过激活函数计算得到的，此外，网络中每一层都与输入层连接，经过实验验证发现，该连接方式有效减轻了梯度消失的问题，并加强了数据特征的传输，有效了缓解了数据集上过拟合的问题，使得数据隐藏特征被充分挖掘，有效的提高了网络预测精度。与残差网络(ResNet)，由于DenseNet网络的每一层都有自己的权重，整个模型参数数量巨大。但DenseNe的不同之处在于，它没有一味的通过加深网络层数来构建网络架构，这种机制有效了提高了参数的利用率，故在反向传播过程中网络需要更新的参数数量较少，模型也更加易于收敛，我们将DenseNet网络结构引入了回归拟合中，激活函数采用了RELU函数[21]。

1.4 模型优化

MBGD是深度学习中应用较为广泛的优化模型，它可以在梯度下降的方向上以很小的步幅来实现更新深度神经网络中每一层的权重和偏置等参数[16-17]。

MBGD算法流程：

输入：样本集的训练集X_train和测试集X_test，迭代次数T，学习率α

初始参数θ

forttoT

从X_train中选取k个样本{xig},i=1,…k,g=1,2,3

g=0

fori=1 tokdo

end for

θt←θt-1-ηgt

end for

输出θ。

2 智能建模试验

2.1 实验数据

珞珈一号01星是首颗兼具遥感和导航功能的一星多用低轨微纳科学试验卫星，2015年由武汉大学立项研制，2018年6月2日发射入轨，其主载荷为夜光成像相机和星基导航增强载荷，主要用于社会经济参数估算、重大事件评估、国家安全等领域，以及开展低轨星基导航信号增强试验。珞珈一号01星的夜光遥感分辨率130 m，可清晰识别道路和街区，优于美国的DMSP/ OLS 2.7 km和NPP/VIIRS 740 m，目前该星已向22个国家和地区(包括美德法英等)3千多用户分发了18万多景夜光影像，为全球不同行业各类用户提供免费数据服务，在社会经济参数估算、国家安全等领域发挥了重要作用[20]。

试验中共选取10 019景珞珈一号01星数据开展实验。为了获取试验数据的无控定位误差，考虑珞珈一号影像分辨率仅为130 m，我们采用google的15 m高分辨率影像作为几何基准，采用全自动匹配的方法将珞珈一号01星影像与google底图进行匹配获取检查点并计算影像的无控定位误差。

2.2 影响无控定位精度的自变量筛选及数据集确定

试验中搭建的神经网络的输入层是：成像姿态参数(三轴向：Xroll是翻滚角，Xpitch是俯仰角、Xyaw是偏航角)、星下点经纬度(Xlat为星下点精度、Xlon为星下点纬度)。珞珈一号01星采用双星敏定姿，因此其成像姿态采用四元数表示，但四元数不利用模型建立。因此，实验前，我们采用四元数与欧拉角的转换公式，将四元数转换成成像三轴欧拉角。数据集的构建具体如下。

表2 数据集构建

在数据集预处理过程中，我们对变量Xn(n=roll,pitch，……，lon)和Y进行了相关性分析，其中Xyaw与Y的相关性为0.000 1，按照统计学的观点，该参数对定位精度的影响可忽略不计。实际上，由于偏航角误差引起的像点偏移表现为像面旋转，其与卫星飞行高度无关，对无控定位精度的影响最小，故在实验进程中，我们将该数据做了删除处理。

在模型构建阶段，数据集划分比例对模型精度产生了一定的影响，在比例为0.6:0.4，0.65：0.35，0.7：0.3，0.75：0.25，0.8：0.2，0.85：0.15下，模型的精度在0.08～0.3中波动，其中在0.75:0.25的比例下，模型得到的预测精度最高，故将所有数据集按照此比例进行划分。划分采用Tensorflow框架提供的train_test_split函数实现。

2.3 智能建模精度验证

文中基于DenseNet结构设计了网络模型，具体各层参数图2所示。

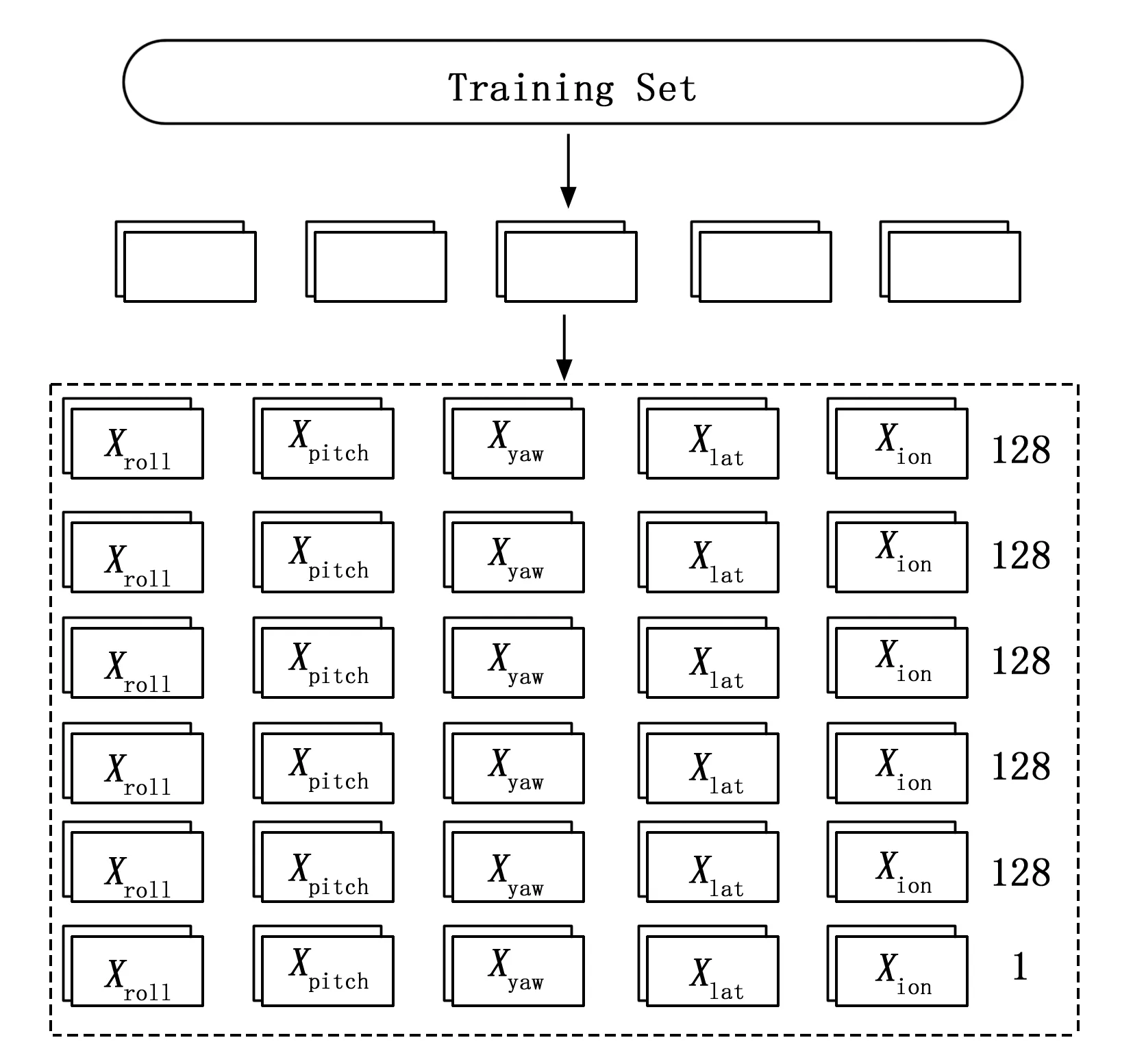
图2 光学卫星无控定位误差智能模型

通过对网络模型的不断调试，最终选择采用包含6层的网络模型，其中1～5层的神经元个数为128个，最终输出层神经元个数为1。实验中，各隐藏层的损失函数如表3所示。

表3 模型各层损失函数

由表3可知，最终模型整体评分为0.846 5，通过对数据集的进一步清理筛选，可以逐步提高模型的稳定性和预测精度。

选取了珞珈一号01星10 019景数据进行实验，数据数量达到3 T，训练集包含参数7 514景数据。模型训练结果如表4所示。

如表4所示，由于珞珈一号01星作为微纳卫星，平台小、搭载的星敏等硬件测量精度较低，其无控定位误差变化较大，试验数据定位误差范围处于41～1 432 m之间，该部分误差主要由于姿态低频误差、姿态测量随机误差等造成。但是，由于引起姿态低频误差、测量随机误差的因素众多，难以建立较为准确的规律模型并通过传统方法求解模型参数，因此较难进行补偿。而文中利用深度学习框架，通过搭建深度学习网络对无控定位误差与星下点经纬度、成像姿态的关系进行训练。利用试验数据中的7 514景影像进行无控定位误差的智能建模，训练得到的模型可以非常准确地预测其余2 505景影像地无控定位误差。表中结果表明，训练网络预测的无控定位误差与真实评估得到的无控定位误差仅仅相差10 m以内，即训练网络可以根据影像成像地星下点经纬度和姿态来准确预测无控定位误差，从而实现定位误差补偿，提升定位精度，如图3所示。

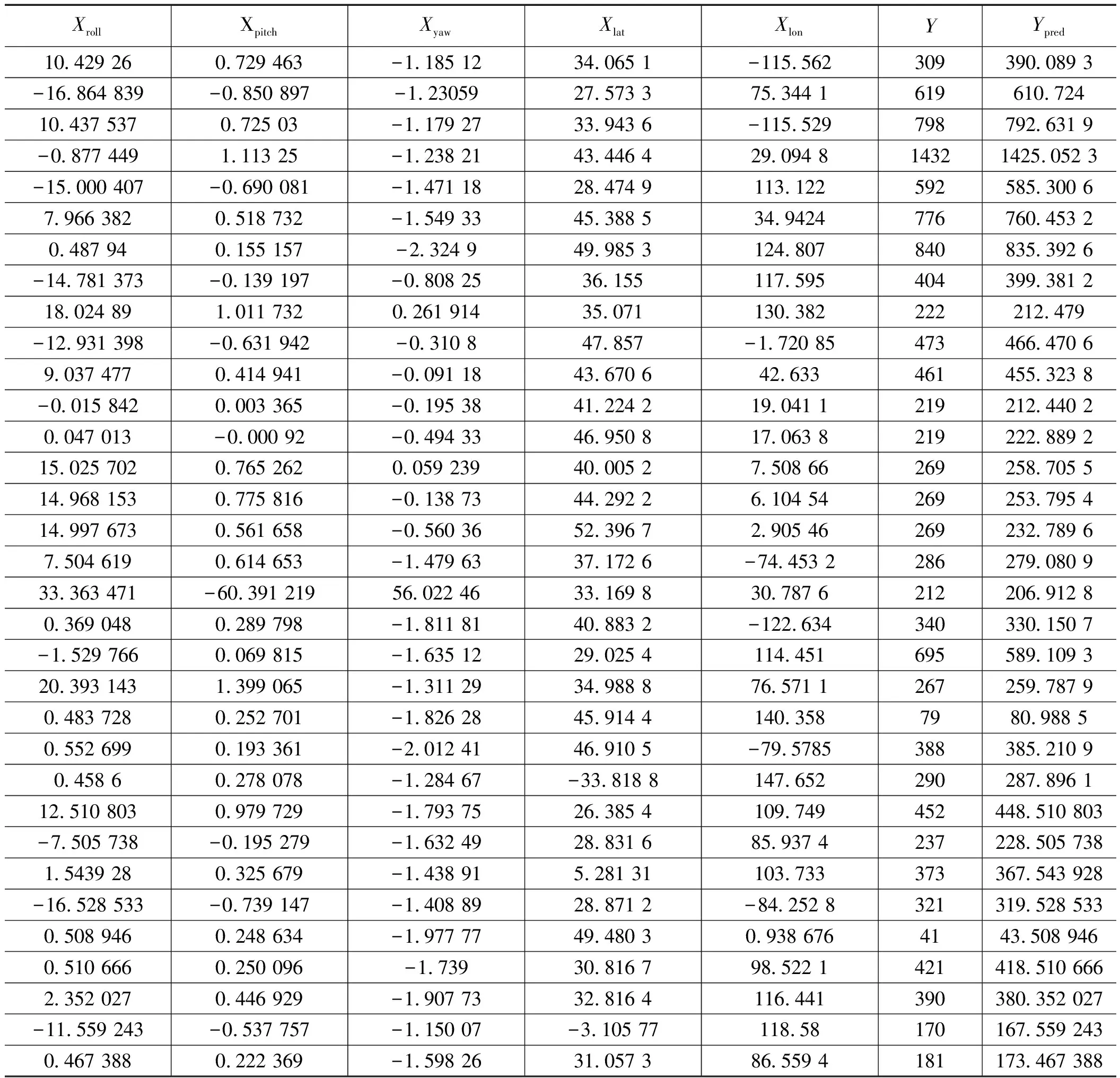
表4 基于珞珈一号真实数据影像定位精度预测结果，Ypred为预测结果

图3 训练网络预测值与真实值偏差

3 结束语

无控定位精度是影响光学卫星影像应用的重要因素。文中从地面处理的角度出发，将卷积神经网络引入定位误差建模，选取卫星成像星下点位置、成像姿态等作为可选变量，利用系统全自动质检获取的无控定位误差与可选变量组成学习样本对，基于深度学习框架，通过DenseNet网络和MDGB优化模型构建了无控定位误差模型。利用珞珈一号真实在轨数据开展试验，试验结果表明，通过对模型进行训练以及验证，模型得到了较高的预测精度，并可根据该模型进行影像定位精度预测，模型预测精度小于1个像素。