基于压电传感器的零点漂移改善电路的研究

王 帅,李 杰，张德彪，孙 宁，江 杰

(中北大学 仪器科学与动态测试教育部重点实验室，太原 030051)

0 引言

在现代化国防时代，制导弹药是国家国防力量的重要体现。为了弹药的顺利列装，列装前需要各项大量的试验测试数据来支撑。其中弹载记录仪就是这些弹体从装填、击发、飞行、毁伤的一系列过程中，对各项动态参数的采集和存储的核心组部件。为了能够实现对目标最大程度地精准打击，提高作战效费比，对侵彻过程的冲击加速度的测量显得至关重要。通过对侵彻目标的过程中采集到的信号数据进行分析和处理，提取信号特征，辅助相关引信技术控制其在合适的时刻启动飞行舵机，展开弹体尾翼，控制起爆时刻，从而完成精确打击。对我国国防事业具有极其重大的意义[1]。

加速度计作为现代动态测试领域中力电转换的核心器件，这类传感器主要分为压电式和压阻式。压阻式加速度传感器为电阻性，低阻抗，压阻式加速度传感器的频率响应范围相对偏窄，在恒定方向加速度下压阻式加速度传感器不输出相关信号，不适合应用在弹体的动态参数的测试。压电式加速度传感器有较宽的频率响应范围，并且在其频率相应范围内具有良好的线性度，但是在使用中需要考虑传感器的电压灵敏度与电荷灵敏度[2]。但是在高过载恶劣环境下，压电式加速度传感器会有零点漂移现象使冲击信号失真，对高过载连续动态参数的测量以及长时间精确参数测量造成不可接受的影响[3]。

本文通过对压电传感器的零点漂移现象的机理分析，提出在前端信号采集的调理电路中用晶体管与运算放大器搭建了加推挽电流放大级的电荷放大器方案，在保持弹载记录仪小型化的原则下，最大程度简化电路分别利用PNP和NPN两个三极管形成推挽电路，增强电路驱动能力，低阻电压输出，使得电荷转换电路中的放电效率大大提升，从信号源头实现补偿优化，在数据不失真的前提下，使侵彻目标时的加速度冲击波形更加平滑，去除由于放电不及时产生的零点漂移现象。

1 零点漂移现象的机理分析

弹载记录仪在恶劣环境下实现对连续高过载动态参数的采集存储。其对具有一定深度的目标进行打击时，由于弹药装填，弹药击发，触靶穿透等一系列动作在短时间内进行，所运用的高精度压电式加速度传感器又普遍存在零点漂移的现象，影响测试中高过载冲击信号的可靠性与真实性。在存在零点漂移的情况下，对所测量的加速度信号曲线进行积分运算时，经过两次积分后弹体速度与弹体行程出现严重误差，无法向导航计算机提供准确数据，从而影响相关引信技术控制起爆时刻[4]，对后期的相关引信技术的研究中造成巨大影响。

在前期初样研制过程中，为获取压电式传感器零点漂移相关信号特征，进行弹载记录仪的高过载冲击试验，试验后由对试验数据处理分析，数据显示测得的侵彻过程原始时域过载曲线如图1所示。

图1 侵彻过程原始时域过载曲线

由图1所示，在575 s左右，原始时域过载曲线中出现严重的零点漂移现象。

在此之前前人普遍创新使用小波分析的方案进行后期数据处理分析。选出消除零点漂移时的最优小波基函数，进行零点漂移的消除[4]。小波分析是针对频率的局部化分析，通过伸缩平移运算对信号进行不同尺度的细化，得到高频、低频不同频域处的细分分析。但是小波分析中包含多种不同的小波类型，常用的是Daubechies小波和Morlet小波，同时还有Haar小波、Mexican Hat小波、Meyer小波、Symlet小波[5-6]。不同的小波有不同的特性，分别用来逼近不同的特征信号，才能得到最佳结果。而且这种算法方案只能适用于事后解算，这明显对于工程实际情况不是最优解。

压电式传感器需要对输出电荷信号进行电压转换，这必然用到电荷放大器。电荷放大器是一种高阻抗，高增益，电容反馈电路[7-9]。当施加交变力时，两极板聚集异性电荷q时，则两极板就呈现出一定的等效电压Uα，即为：

(1)

其中:C为压电等效电容量。

(2)

式中,A为极板面积；h为极板厚度；ε压电晶体的介电常数；εr为压电晶体的相对介电常数；ε0为真空介电常数；压电传感器极板电容都存在等效的泄漏电阻，对压电传感器来说，交变力会引起电荷产生，而这些电荷电量q随后就通过泄漏电阻逐渐泄放完毕。但是由于电荷放大器的高阻抗特性，导致压电传感器在达到采集最高值时电量没有完全释放出来，在以后在采集过程中一直存在缓慢放电现象，对之后的采集信号造成不可预估的影响，从而产生了零点漂移的现象[1]，所以解决零点漂移问题的核心在于控制电路放电效率。

2 对加速度信号测量电路的研究

2.1 基于跟随器电路的分析

对压电式传感器输出电荷信号的测量，采用电压放大器的高阻跟随器电路如图2所示，用等效输入电阻Rin和等效输入电容Cin表示，其中等效输入电容包括跟随器输入端电容，以及从传感器到跟随器的传输线等效电容。

图2 高阻跟随器电路

由于输入等效电容Cin对测量的影响，以及实际测量信号是由正弦波构成，所以不考虑阶跃方波信号等其他信号的信号调理分析，此时有式(3)：

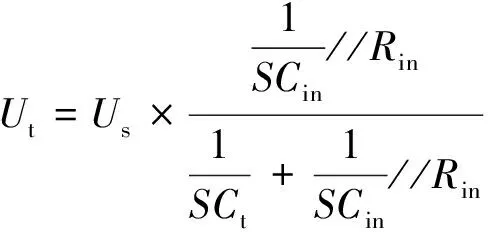
(3)

(4)

其中：Us为原始输入信号，Ut为跟随器输入信号。写成频域表达式为:

(5)

此时有：

可见其中的频率增益和特征频率都受到Cin的影响。但是Cin具体的值在实际情况中无法确认，所以我们只能尽可能减小Cin的值，但是我们无法判端实际情况中能否将Cin降低到足够小，所以我们的跟随器方案不能满足实际运用条件，就需要考虑使用电荷放大器。

2.2 基于电荷转换电路的分析

在基于电荷转换电路的原理分析的基础上，针对电荷放大器零点漂移现象，建立核心元器件的等效电路模型，如图3所示，图中US为压电式加速度传感器等效激励源，CS为压电式加速度传感器的等效极间电容，Rd为电荷放大器的等效输入阻抗以及信号传输导线电阻之和，CIN为电荷放大器的等效输入电容与导线电容之和，Cf为电荷放大器的反馈电容，Rf为电荷放大器的反馈电阻，反馈电阻是为了避免偏执电流持续为反馈电容Cf充电导致反向电压饱和而存在的，UIN+与UIN-为电荷放大器正向输入端与反向输入端的电压，由于运放的输入阻抗近似与无限大，所以在常规电路中通常将UIN+接地，视为0 V[10]。

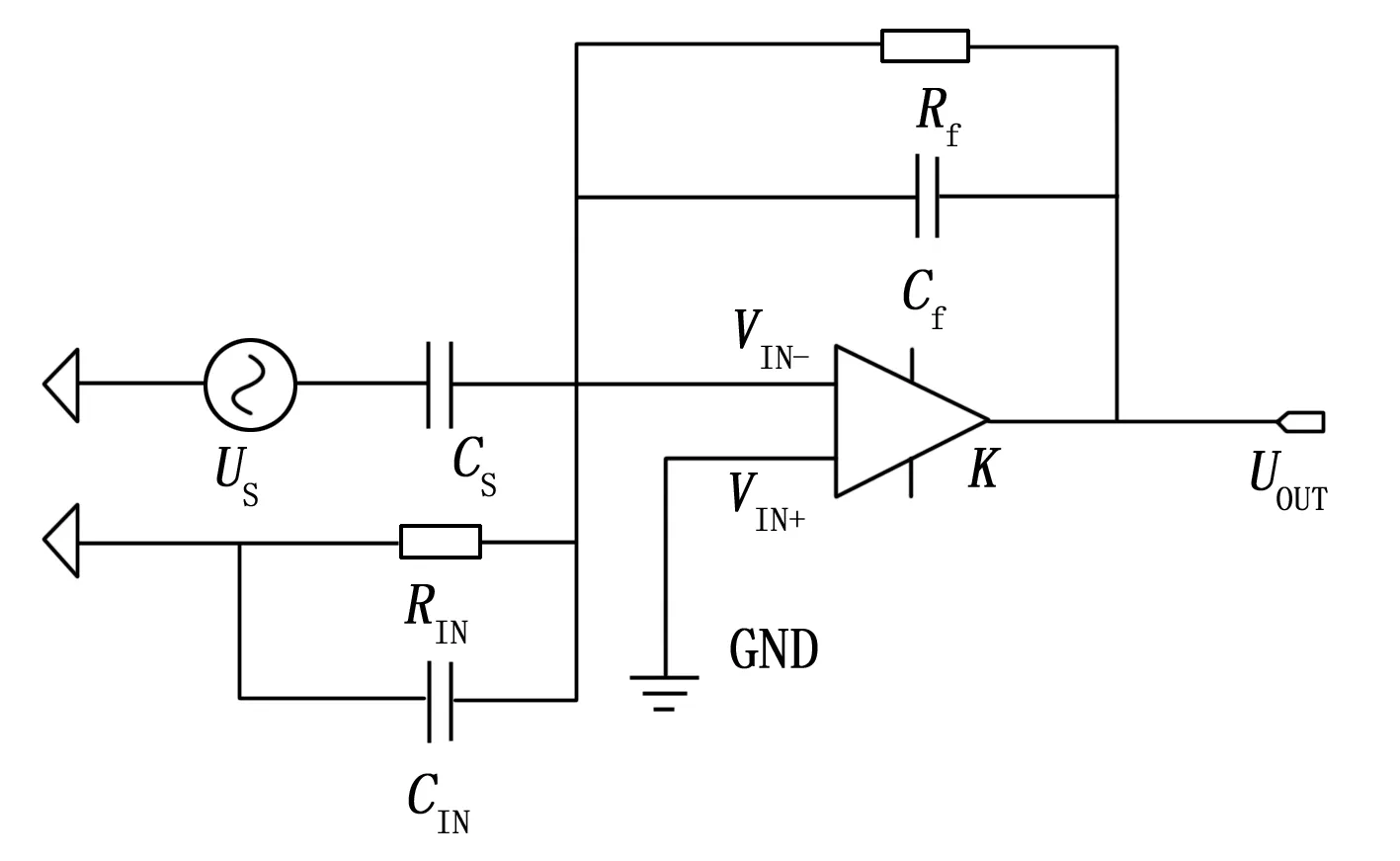
图3 电荷转换等效电路

对于图3的电荷转换等效电路，运用基尔霍夫电压定律(KVL， Kirchoff’s voltage law)，基尔霍夫电流定律(KCL，Kirchoff’s current law)[5-7]，在图3中的A点通过节点电压可得：

(6)

其中:T为时间常数，即为电容充电饱和时间的倒数。化简式(6)可得：

(7)

UIN+接入等效地，视作0劳V，为开环增益，由于运算放大器的开环增益特性可知：

VOUT=K(UIN+-UIN-)=-KUIN-

(8)

将式(8)代入式(7)可得UOUT表达式，为简化公式，我们定义CALL=Cf+CS+CIN：

(9)

本设计使用的是电荷敏感型传感器，故将传感器激励源电压与传感器输出电荷量Q之间的关系式导出：

(10)

将式(10)代入式(9)中:

(11)

由上式可知，消除了US压电传感器激励源的影响，反馈电阻Rf主要影响电荷放大器的截止频率，我们对反馈电阻Rf尽量选择阻值较大的电阻，从而使得截止频率的下限尽可能小一些，对零点电压漂移不产生直接影响。所以主要针对CALL进行调整分析，从而改变VOUT即零点漂移的输出电压。CALL由CS、CIN、Cf组成。CS为压电式传感器极间电容，这属于传感器特性，不可改变。CIN为输入电容与电缆电容之和，同样是固定属性。所以反馈电容Cf是关键因素，Cf容值越小增益越大。从而达到电荷放大器的相关参数进行调整，对电荷放大器的漂电压进行修正。

2.3 基于推挽电路的分析

推挽电路是使用两个相同的功率的三极管，以推挽的形式存在于电路中，分别负责正负半周期的波形放大任务。两个三极管的输出在负载上合并得到完整周期的输出信号[11]。要向负载提供足够的输出功率，即电压电流都放大的情况，此时最大输出功率为：

(12)

式中,Ucem为集电极输出的正弦电压，Icm为集电极输出的电流。

电路的效率为：

(13)

式中,P0为放大电路输出给负载的功率，PV为直流电源VCC提供的功率。

如图4所示，使用PNP型三极管代替发射极负载电阻，NPN型三极管将电流推给负载，PNP型三极管吸收电流。

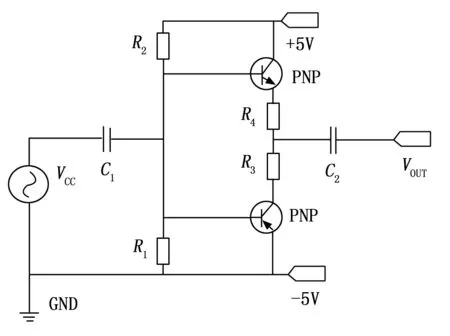
图4 推挽电路

对图4中的推挽电路进行Multisim电路仿真，得到的仿真输出波形如图5所示。

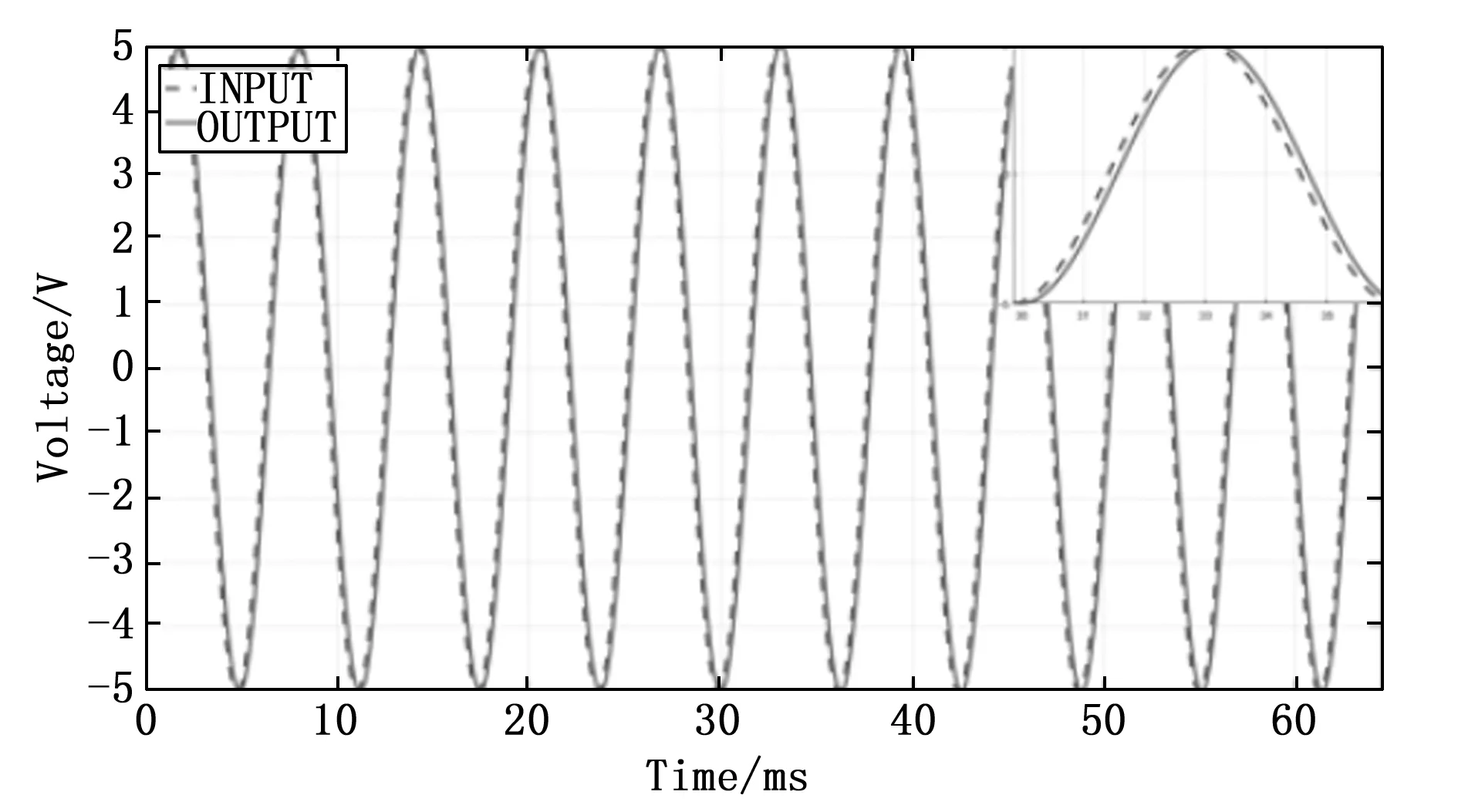
图5 推挽电路仿真波形

看到图5中放大的推挽电路仿真波形，可见输出波形并没有完全被截去，在0 V附近出现了交越失真的现象。这是因为在实际运用中，把不为零的门限电压视作为零，而且在三极管输入电压较低的情况下，输出电压存在着死区，在这段区间内，电压和电流的关系不是线性的，三极管基极与三极管发射极电位差小于0.7 V，三极管截止，所以在输出波形中央产生±0.7 V的死区。

为了改进电路中的交越失真，加入二极管消除晶体管盲区[12]。加入二极管后，使得两个三极管的基极与发射极之间的电位差为0.5 V，输入信号在0 V附近变化时，发射极能导通，可见二极管抵消了晶体管的交越失真。抵消后波形如图6所示。

图6 抵消交越失真现象后的波形

3 加速度测量电路的系统级设计

3.1 系统级设计

根据上文，试验现象与分析结果，设计弹载高精度数据记录仪。系统主要由传感器信号调理电路、高速模数转换电路，FPGA(field programmable gate array)采集控制电路，Flash存储电路，通信接口电路，内部电源模块等部分组成[13]。系统总体框架如图7所示。

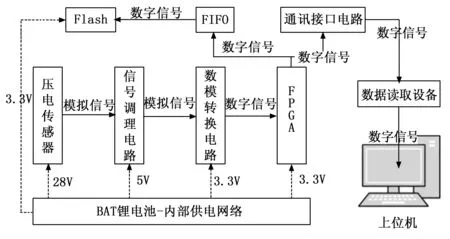
图7 弹载记录仪的总体框架图

系统供电网络采用7.4 V-500 mAh的锂电池通过级联降压的方式进行电压转换，以便于为各电路子模块和前端传感器供电。FPGA采集控制电路控制高速模数转换器对经过信号调理电路的压电传感器信号进行采编，经过FIFO(first in first out)跨时钟域缓存后写入NAND Flash。待试验结束后，通过数据读取设备和上位机软件将弹载记录仪中的数据读取至上位机。最后通过数据处理软件进行相关传感器的数据处理，获取完整测试信号。

该信号调理电路如图8所示，该电路分别用两种不同极性的晶体管间组成推挽电路，增强其驱动能力[14]。PNP型和NPN型三极管以推挽的形式存在于电路中，各自负责正负半周期的波形放大任务。此处的Cf应当尽量选择高泄露小容值电容，这里使用的是1 nF的电容，具有良好的吸附效应。同时这里运用的运算放大器OPA129U的输入电阻可不做过多考虑，它自身具有1013Ω的差模输入电阻[11]。运算放大器输出端接5.0 V的钳位二极管，以保证在测量信号在超量程时输入推挽电路的电压不会超过5.0 V[15-16]。保护后端高速模数转换芯片在正常工作中不会因此受损。

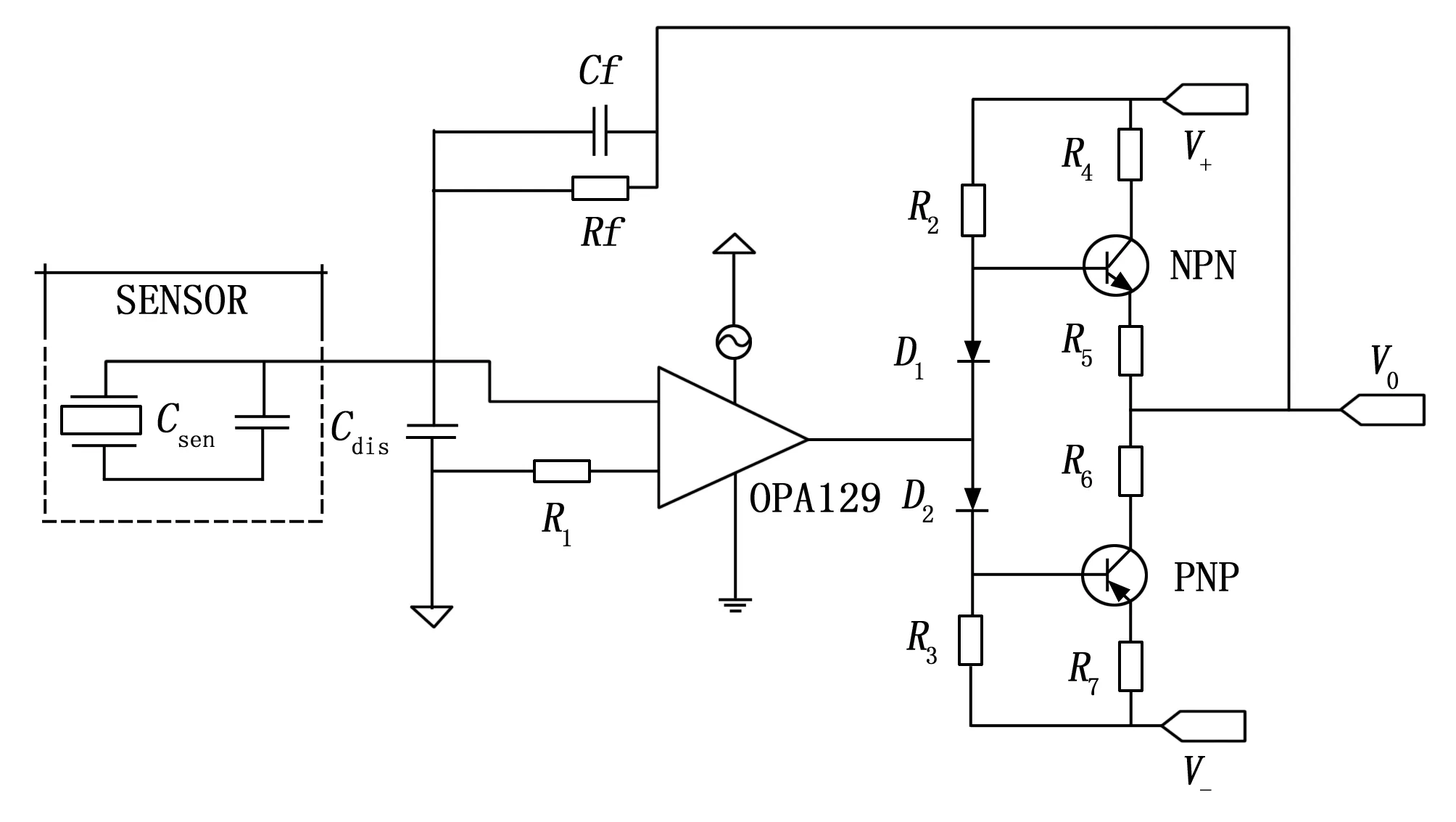
图8 信号调理电路原理图

使用传感器频率响应相似的信号对整体信号调理电路进行仿真，仿真结果如图9所示，可以完整采集模拟信号值。

图9 信号调理电路仿真波形

系统集成后固化处理，使用马歇特锤击模拟高过载冲击试验，得到高过载冲击信号数据，如图10所示。

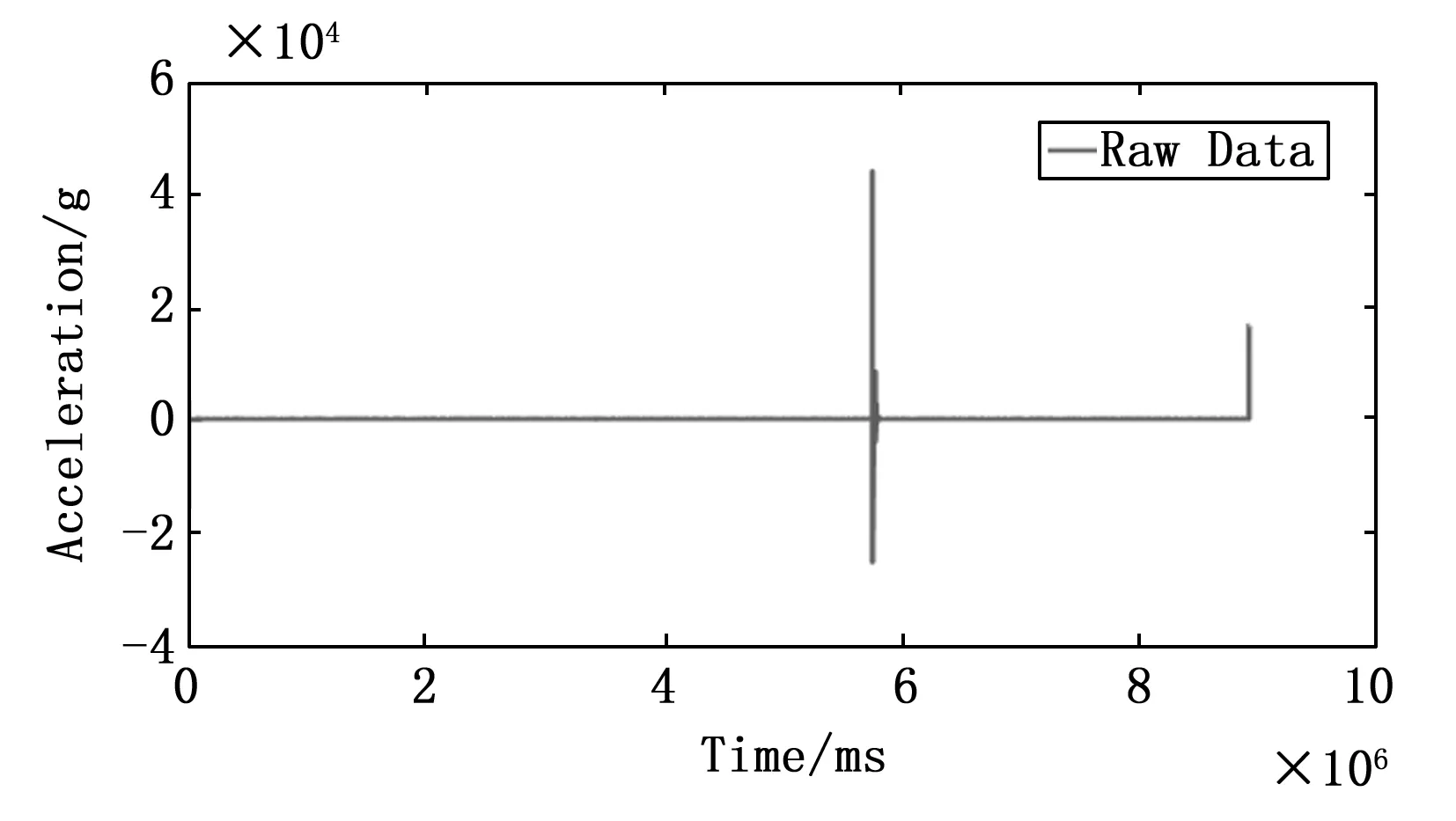
图10 高过载冲击信号曲线

可以明显看出在高过载冲击的恶劣环境中，本研究设计的信号调理电路已经去除压电传感器的零点漂移现象。

实测过程中过载峰值与理论预算值差距较大，实测值明显大于理论预算值。我们对得到的测试冲击信号进行分析。在信号分析领域有许多处理方法和工具，其中最常用的是傅里叶变换，它将时域信号转换为频域信号，从而可以在频域对信号进行分析[18-19]。对于图10所示的数据进行快速傅里叶变换(FFT，fast fourier transform)，进行频谱分析。得到频谱如图11所示。

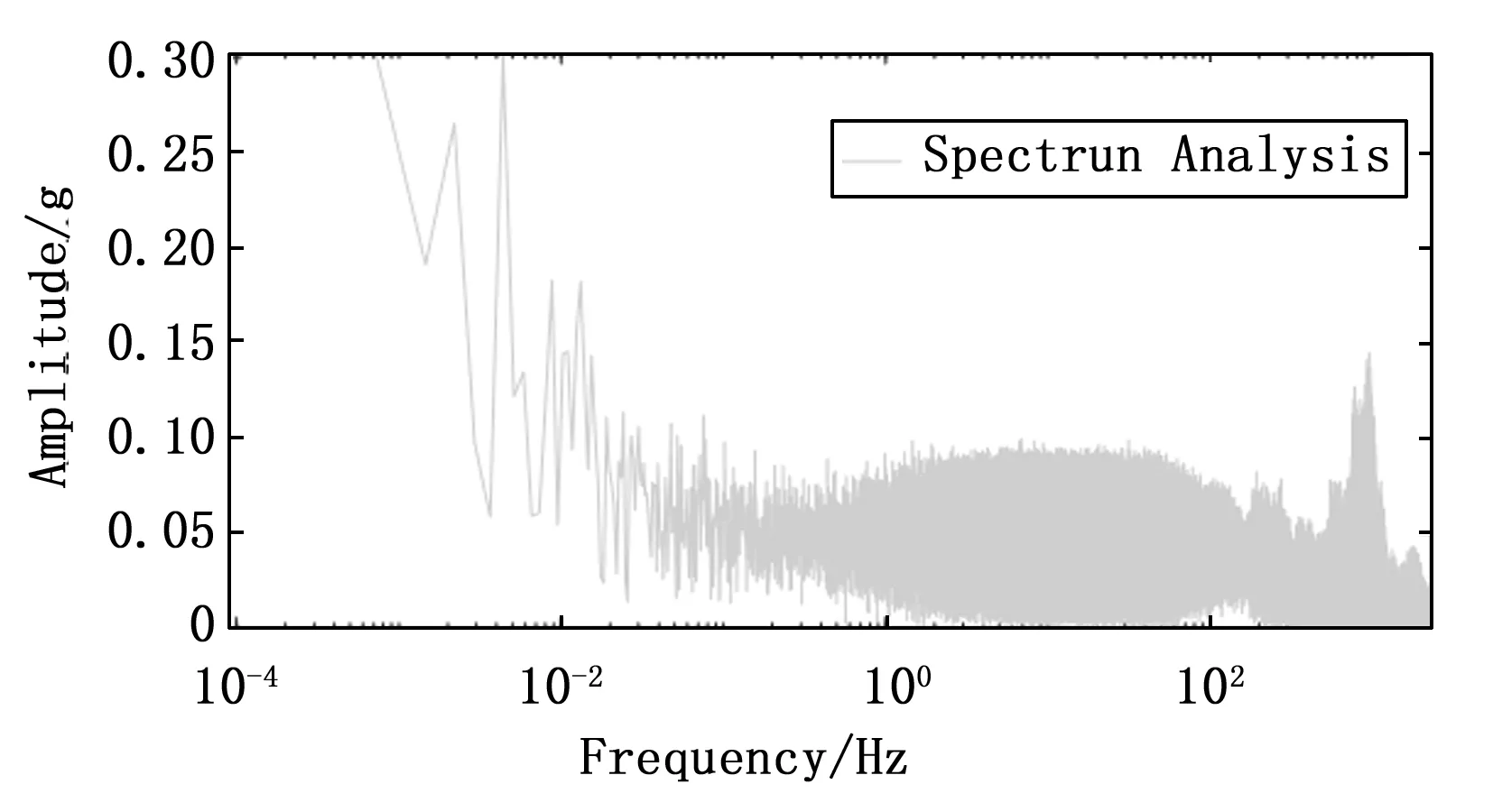
图11 高过载冲击原始数据频谱分析

在频谱中存在高频信号，101～104Hz混入整体信号频谱中，预测造成这种现象是由于试验环境中弹载记录仪与试验设备刚性硬连接，模拟侵彻过程中混入多种频率噪声，产生传感器自振与机械共振的现象，共振是指机械系统所受力学激励的频率与该系统的固有频率相接近时，系统振幅显著增大的现象[17]。对于压电传感器来说，共振现象会造成采集的信号值峰值增大，并且会造成对于峰值出现的时间不确定性，最终导致冲击信号失真，降低信号可信度。根据所选压电式加速度传感器数据手册，可知其主要参数如表1所示。

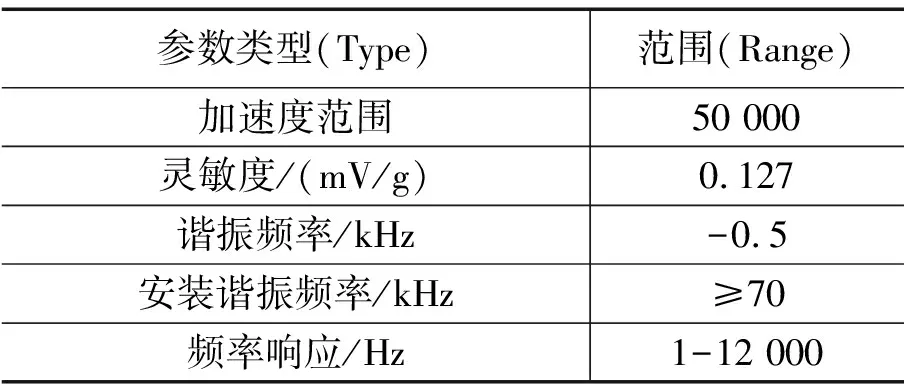
表1 压电式加速度传感器主要参数

可见所用的压电式传感器的频率响应为1～12 kHz。安装的机械谐振频率大于70 kHz，正好符合我们的预初分析，所以在频谱图中，频率大于12 kHz的信号肯定不是传感器所采集到的正常信号。为了保证信号不失真以及信号可信度，并且消除信号中高频谐振与传感器自振造成的振动幅值增大的现象以及实现抗混叠滤波，必须选用低通滤波器滤除信号噪声。

根据对实测数据的频谱分析结论可知，有效信号基本保留在10 kHz以下，在后期进行数据处理解算的过程中，使用数据处理软件进行10 kHz低通滤波操作验证预先设想，得到高过载冲击信号如图12所示。此时接近真实值，与理论预算值基本吻合，在添加滤波操作后，可以完全实现动态常规弹药侵彻过程过载连续动态特性的测量。

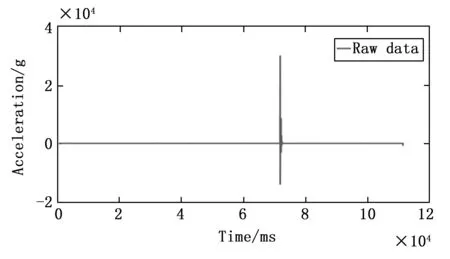
图12 10 kHz低通滤波后的冲击信号图

为了更加符合设计初衷，实现完成动态常规弹药侵彻过程过载连续动态特性测量的最简化操作，尽可能去除一切需要事后数据处理的操作。在不更改硬件电路以及不添加附加设备基础上，在FPGA的环境下，利用FIR(finite impulse response)滤波器实现对信号进行低通滤波操作。

不同的FIR类型可以设计不同类型的滤波器。各种窗函数的频谱特征主要区别在于主瓣宽度，幅值失真度，最高旁瓣高度与旁瓣衰减速率等参数[10]。利用Matlab中选择一定的窗函数进行FIR滤波器的参数设计，常用的窗函数参数如表2所示。

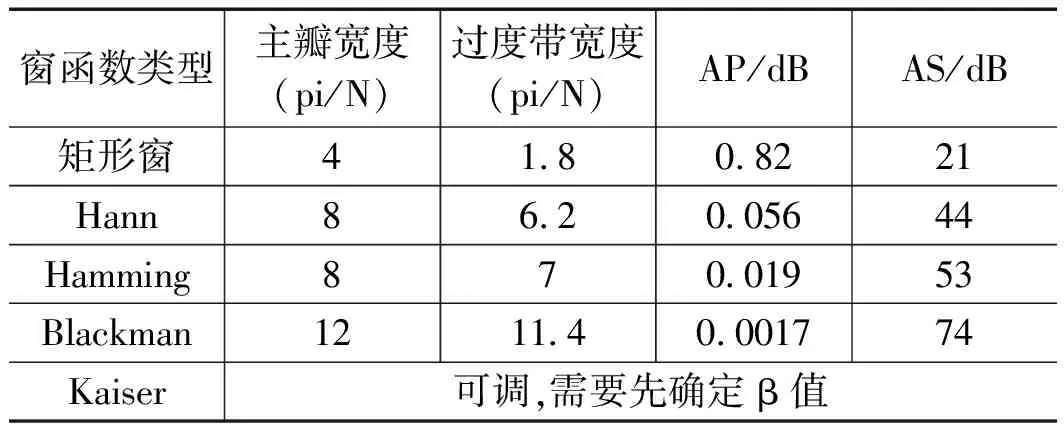
表2 窗函数主要参数选择

在基于窗函数的基本概念下设计滤波器的本质是选择一种合适的理想频率选择性滤波器，然后将它的冲激响应截短，以获得一个具有线性相位的FIR滤波器[20]。因此这种方法的关键是选取某种响应频率较好的窗函数，在滤1波器性能给定的情况下，尽量选择主瓣窄，旁瓣峰值小的窗函数。实现FIR滤波器的过程其实就是实现卷积和累加的过程，公式如下式所示：

图14 Verilog中实现低通FIR滤波器

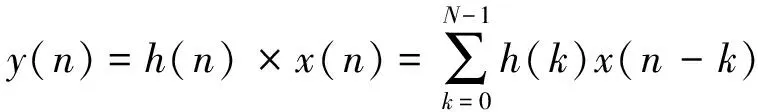
(14)

从式(14)中可以看出，x(n)是我们的待滤波信号，h(n)是滤波器抽头系数，卷积的过程其实就是一个相乘、累加的过程[21]。

确定滤波器的阶数M，需要先确定滤波器的长度N，对于除了Kaiser窗以外的窗函数，比如Hann窗，N的值由下式(15)可以推算出：

N=mod(N+1,2)+N

(15)

阶数M为N-1且为偶数所以用FPGA实现8阶FIR滤波器的主要分成三级流水线，如图13所示。第一级流水线将输入信号延时，每到来一个时钟信号，便将输入信号保存至寄存器，然后，之后的输入信号会进行移位操作；第二级流水线将经过缓存的输入信号与滤波器系数相乘，每到来一个时钟就将乘积结果更新到寄存器中；第三级流水线将输入信号和滤波器系数相乘结果累加起来输出。

图13 FIR滤波器实现原理

通过Vivado调用乘法器DDS IP核，将两个正弦信号进行混合频率处理，然后输入至FIR滤波器IP核的wave_in端口，在Vivado中进行程序仿真，使用Hann窗设计FIR滤波器的参数，观察FIR滤波器的滤波功能实现，如图14所示。

4 试验验证与分析

在方案论证通过后，系统集成使用环氧树脂进行灌封固化处理，再进行使用马歇特锤击模拟过载冲击试验，现场如图15所示：模拟在实弹环境下的常规弹药侵彻过程高过载连续动态特性的测量试验，测试零点漂移现象的改善与实时滤波效果。

图15 马歇特锤击试验

将马歇特锤击试验的参数调整至验证试验同样参数，获得过载幅值相近，冲击频谱相似的冲击信号。弹载记录仪在试验过程中表现良好，弹载记录仪冲击信号如图16所示。

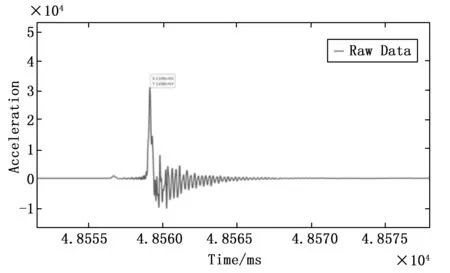
图16 弹载记录仪冲击信号

由图可见，基于压电式加速度传感器高冲击侵彻加速度测量电路可以实现在信号源头处解决由于高过载引起的零点漂移问题，并且系统在FPGA中实现实时低通滤波，逼近真实数据，获去真实动态参数，完全解决所有需要事后进行的数据处理操作，简化整体弹体连续动态参数测量的实验步骤，一定程度上缩短了弹药的研制周期。

5 结束语

本文介绍了基于压电式加速度传感器高冲击侵彻加速度测量电路中零点漂移现象改进的相关研究，提出了一种可以解决侵彻过程中由于高过载导致信号调理电路放电不及时所产生零点漂移现象的解决方案，并且在FPGA中实现实时低通滤波，逼近真实数据，获去真实动态参数。相比前人在此科研方向上的小波分析，寻找最合适的小波基与分解层数进行后期数据处理，对测试人员的基本素养要求较高，此方案更具有实时性，有效降低测试时间与经济成本，在零点漂移产生原因的根源处的信号源头解决此类问题。经过理论分析、试验验证以及靶场实弹试验证明，此方案确实可行，能满足测量常规炮弹侵彻过程高过载连续动态特性的测量，对研究这类工程问题的人员实现对测量电路改进具有指导意义。