砂岩球形颗粒多点接触破碎试验
2022-03-29牛奕然
牛奕然,周 健,赵 程,李 琳
(1.陕西建工第一建设集团有限公司,陕西 西安 710003; 2.同济大学岩土及地下工程教育部重点实验室,上海 200092;3.同济大学地下建筑与工程系,上海 200092)
近年来,我国在超高坝领域飞速发展,作为坝体主要材料,粗粒土在高应力作用下的破碎问题引起了国内外诸多学者的关注[1-6]。目前针对粗粒土颗粒破碎的研究主要基于宏细观力学性质进行探讨[7-10],以单个颗粒的力学特性为对象的研究较少。
影响粗粒土单个颗粒破碎细观特性的因素较多。目前对于接触破碎过程中颗粒内部力学机理的研究尚处于初期阶段,一些学者从颗粒的形状、尺寸、材料、接触点数量、接触形式和受力条件等影响因素出发,探究各因素对粗粒土颗粒破碎特性的影响,试图从细观角度揭示其力学机理。如Zhao等[11]将颗粒间接触形式简化为点-点和点-面接触,研究了法向受压条件下,材料、接触形式以及颗粒尺寸对粗粒土颗粒接触破碎特性的影响。在初期的基础研究中,颗粒形状的差异会造成接触形式、受力条件等诸多影响,因此在研究其他影响因素时,暂时排除了颗粒形状的干扰。同时,球形颗粒接触破碎过程中内部应力状态对不规则形状颗粒接触破碎特性的研究具有可参考性[12-13],因此近些年来,一些学者从最简单的球形颗粒出发,试图揭示粗粒土颗粒间接触破碎的细观力学机理。如周健等[14-15]探究了大理岩球形颗粒之间的切向接触破碎特性;Yu等[16]研究了石膏球和刚性板之间法向受压破碎,并通过数值模拟手段探究了点-面接触形式下球形颗粒内部破碎过程的力学机理。综合材料、接触形式和受力条件等因素,周健等[17]分别对砂岩、石灰岩和板岩球形颗粒进行点-点接触破碎试验,拟合出岩石材料球形颗粒单点接触破碎的锥形核尺寸和发生整体破碎时临界力的经验公式,该公式仅适用于单点接触破碎,具有一定的局限性。实际工况中,单个颗粒会与周边多个颗粒同时接触从而存在多个接触点,因此有必要进行球形颗粒群的接触破碎试验。本文利用砂岩材料进行球形颗粒群接触破碎的可视化试验,对试验中的每个球体进行统计,在已有单点接触破碎规律的基础上,完善多点接触条件下锥形核尺寸及破碎率的经验公式。试验主要用于对多点接触条件经验公式的完善,因此同样采用球形颗粒。而实际工况中颗粒形状不规则,颗粒形状对破碎规律产生的影响需要进一步研究和完善。
1 试样材料、设备与试验设计
1.1 试样材料
关于球形岩石颗粒单点接触破碎特性的相关经验公式是基于砂岩、石灰岩和板岩3种材料的试验结果拟合得出的[17]。笔者对该公式和结论进行多点接触条件下的修正和补充,认为材料属性对公式的修正和破碎规律影响较小,因此材料选取粒径分别为2 cm、5 cm的砂岩球形颗粒。在进行颗粒群破碎试验前,对风干后的砂岩材料进行了标准圆柱体试样的单轴压缩试验(直径50 mm,高度100 mm)和巴西劈裂试验(直径50 mm,高度50 mm),得到材料的弹性模量为20.7 GPa,泊松比为0.29,单轴抗压强度为57.6 MPa,抗拉强度为3.9 MPa。
1.2 试验设备
使用的离心机设备隶属于同济大学岩土及地下工程教育部重点实验室,是由中国工程物理研究院总体工程研究所研制的TJL-150复合型土工离心机,其最大容量为150 g·t,最大离心加速度为200 g,有效旋转半径为3.0 m。
土石坝离心模型试验中的超径颗粒主要影响土体的抗剪强度,缩尺后的颗粒在同样的应力条件下,其破坏性试验通常会与原型颗粒产生较大的差别[18]。本文研究的主要为球形颗粒的破碎问题,上部堆载虽与颗粒群相互作用,但其主要作用为竖向压力,颗粒间无相对位移,不考虑颗粒群的结构性破坏,且锥形核尺寸与颗粒粒径属同一维度,同比例变化,因此试验采用原型试验中的颗粒粒径,不进行缩尺操作。
1.3 试验分组与试验过程
试验共7组,试验Ⅰ~Ⅴ和试验Ⅴ~Ⅶ分别用以研究不同荷载水平和不同粒径下的接触破碎,试验分组情况如表1所示,模型尺寸和球体的排列方式如图1所示,其中试验Ⅰ~Ⅴ采用粒径为5 cm的颗粒;试验Ⅵ采用粒径为2 cm的颗粒;试验Ⅶ采用混合粒径,5 cm颗粒排列方式同试验Ⅰ~Ⅴ,2 cm的颗粒填充于大球空隙。
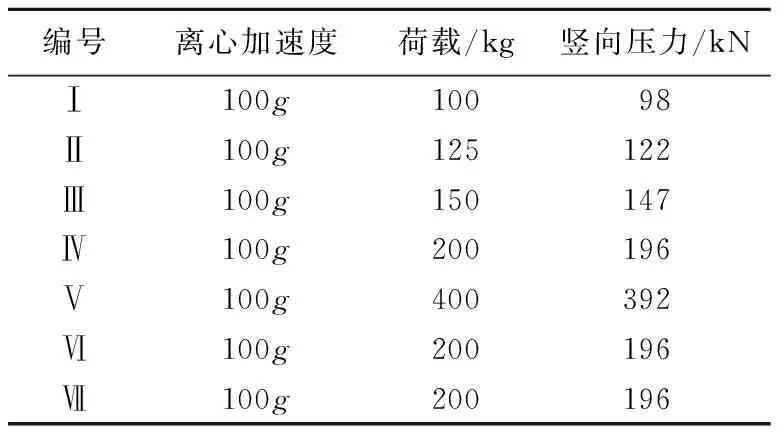
表1 试验分组情况
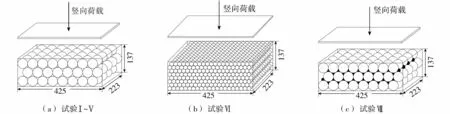
图1 颗粒排列方式(单位:mm)Fig.1 Arrangement of particles(unit:mm)
试验前对刚性接触面(模型箱顶板、底板和侧壁)涂抹机油进行充分润滑,以消除边界摩擦对试样的影响。在箱内分层装样,使颗粒尽量分布均匀,每层分别压实。摆放完毕后,静置一段时间,保证颗粒群内部法向接触力分布均匀,然后在试样顶部摆放钢板进行加载。加速度按照10g的增量递加,在每级加速度下维持5~10 min时间,变形稳定后,再进行下一级加载,直至试样在最后一级加速度下变形稳定。每组试验结束后,对破碎球体进行拍照并用塑料袋逐个保存。
2 试验结果与分析
2.1 破碎形态分析
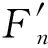

图2 单颗粒受力分析示意图Fig.2 Schematic diagram of force analysis for single particle
表2为试验Ⅳ中球形颗粒的破碎形态和位置分布统计。由表2可知,两块类试样在颗粒群中的位置分布较为均匀,3块类试样则主要分布于第1、3层。根据图2受力分析可知,球形颗粒的破碎形态与其受力状态有关。若定义两颗粒间受力的接触点为有效接触点(若接触点不受力则为无效接触点),则第1、3层每个颗粒有效接触点数为3(3点接触),第2层每个颗粒有效接触点数为4(4点接触)。由此可知,3点接触比4点接触更利于球体形成3块类的破碎形态。与单点接触破碎结果进行对比,结果表明,接触点为3及以上是发生3块类破坏的必要条件,且3点接触条件下,球体更容易发生3块类破坏。

表2 试验Ⅳ破碎形态及位置分布
通过对破碎试样的观察,得到3块类试样破碎情况,如图3所示,图中数字为接触点编号。分析可知,1、2接触点形成了平行于纸面的破裂面(线状条纹所示区域),1、3接触点形成了与之不同的破裂面(点状条纹所示区域),因此形成3块类破碎形态的原因是球体在3个接触点作用下,分别形成了2个不同的破裂面,若形成相同的破裂面,则会发生两块类破坏。
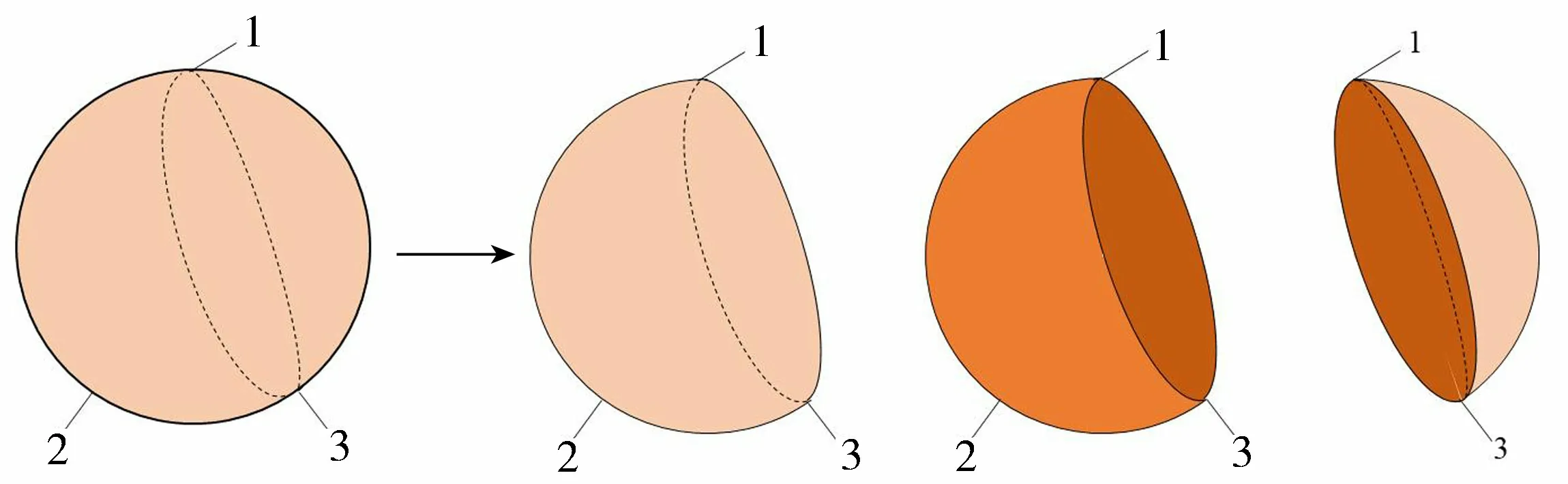
图3 3块类试样破碎特征Fig.3 Crushing characteristics of three-block type samples
2.2 锥形核分析
岩石材料球形颗粒单点接触破碎的锥形核尺寸和发生整体破碎时临界力的经验公式[17]如下:
(1)
(2)
FCr= 0.200D+ 0.024E- 2.496
(3)
式中:S为锥形核底面积,mm2;H为锥形核高度,mm;D为颗粒粒径,mm;σc为材料单轴抗压强度,MPa;σt为抗拉强度,MPa;FCr为破碎力,kN;E为弹性模量,GPa。
试验中球体均为多点接触,破碎时产生多个锥形核。已知球形颗粒发生整体破碎均是由一个主锥形核刺入并导致球体发生张拉破坏,因此只统计破碎试样的主锥形核尺寸(尺寸最大的锥形核)。
根据图2的受力分析,第2层颗粒破碎时主锥形核所在接触点受到的法向力小于第1、3层颗粒:
(4)
统计试验Ⅰ~Ⅳ中每层破碎颗粒主锥形核的底面积和高度如图4所示(利用游标卡尺分别测量底面直径和高度)。由图4可知,随着颗粒在发生整体破坏瞬间接触点处法向力的增大,锥形核的底面积和高都会增大,且两者基本呈线性关系。由式(4)可知,锥形核底面积与材料拉压比成反比,与颗粒粒径的平方成正比。结合试验,其与发生破碎瞬间接触点所受法向力成正比,于是拟合得到多点接触条件下锥形核底面积经验公式:
(5)
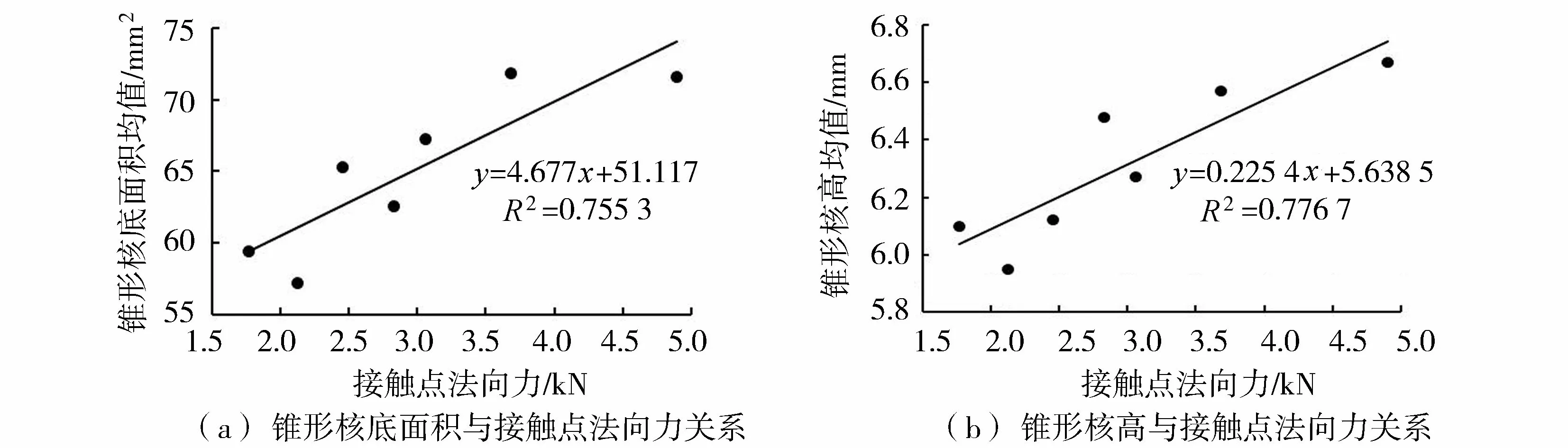
图4 锥形核尺寸与接触点受力关系Fig.4 Relationship between the size of cone-shaped core and the force acting on the contact point
式中:F为球体破碎时接触点处法向力,kN。由式2可知,锥形核高与材料拉压比成正比,与粒径成正比,且根据试验,与接触点所受法向力成正比,于是拟合得到多点接触条件下锥形核高经验公式:
(6)
式(5)(6)可用于估算不同材料、不同粒径球形粗粒料颗粒群接触破碎时锥形核尺寸的大小,且为其数值模拟提供依据。
2.3 破碎率分析
球形颗粒发生整体破碎时的临界力FCr是针对单个颗粒的物理量。对于球形颗粒群,由于竖向荷载较小时并非所有的颗粒发生破碎,因此研究破碎率更具有实际意义。使用每组试验中发生破碎的颗粒数量与颗粒总数量的比值表示破碎率。经统计,试验Ⅰ~Ⅴ中破碎率与竖向荷载的关系见图5。由图5可知,竖向压力低于100 kN时,仅有1个颗粒发生破碎,当竖向压力达到100 kN并逐渐增大时,破碎率不断增大,并最终趋向于100%,曲线斜率不断变小。
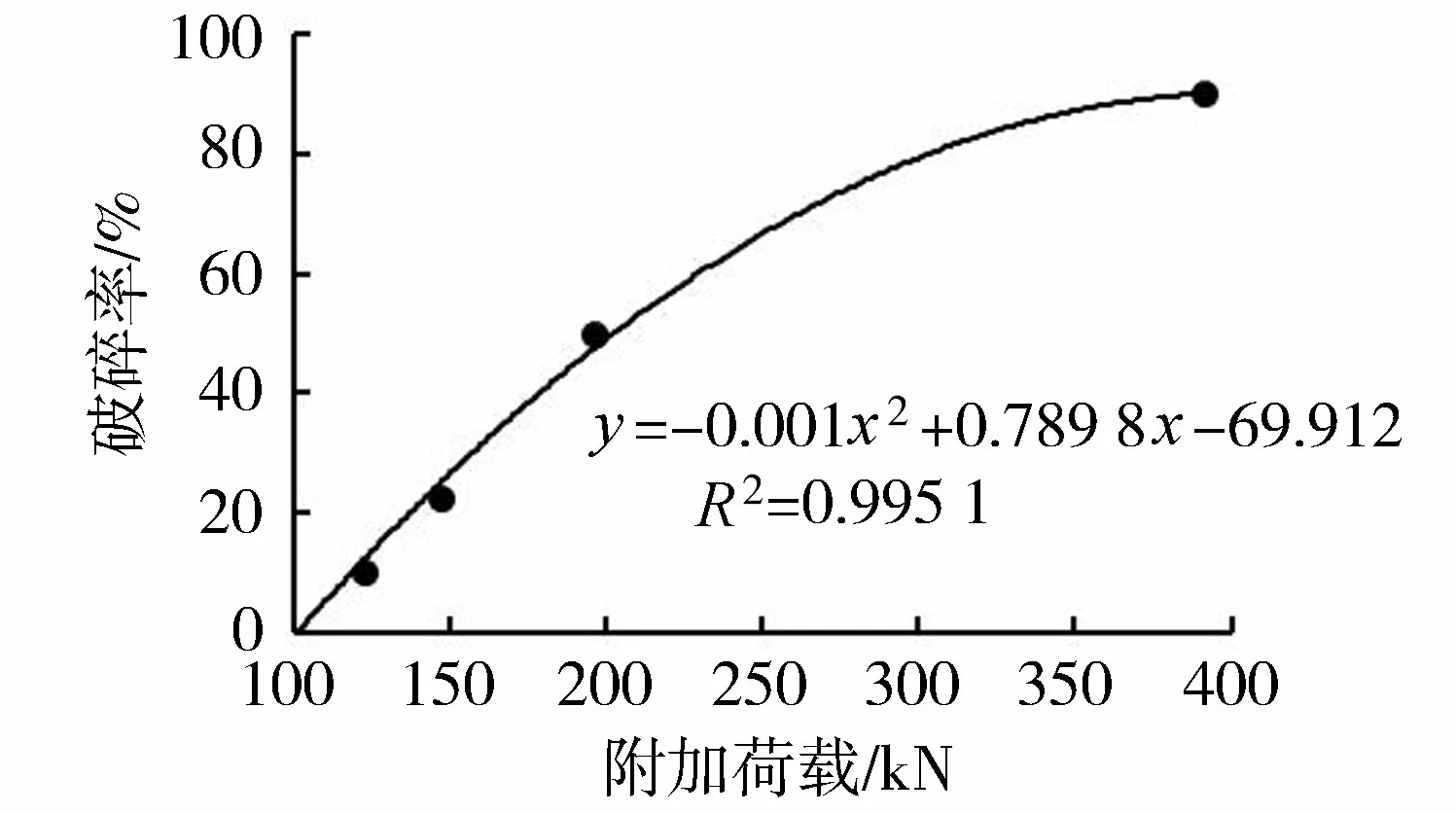
图5 破碎率与竖向荷载关系曲线Fig.5 Relation curve between crushing rate and vertical load
由式(3)可知,影响球形岩石颗粒接触破碎时法向临界力的因素有材料的性质和颗粒粒径,竖向荷载条件相同时,粒径的平方与荷载施加在单个颗粒上的力成正比,且材料性质仅影响单个颗粒强度。通过拟合,可得破碎率与竖向荷载的经验公式:
B=[-(0.396D2P+ 0.200D+ 0.024E- 14.276)2+ 100] × 100%
(7)
式中:B为破碎率,%;P为单位面积竖向荷载,GPa。
利用式(7)计算得到试验Ⅵ的破碎率为7.15%,试验中测得其破碎率为7.6%,可验证该经验公式具有一定的可靠性。分别将B=0和B=100%代入式(7),可得:
(8)
(9)
式中:Pmin为开始产生颗粒破碎所需单位面积最小荷载,GPa;Pmax为颗粒全部破碎所需单位面积最小荷载,GPa。
由此可得单一粒径条件下球形颗粒群的破碎规律,即:当P
(10)
表3为不同荷载条件下每层颗粒破碎数量。由表3可以发现,第2层颗粒的破碎数量明显小于第1、3层,因此竖向荷载相同的条件下,位于颗粒群内的颗粒,由于接触点数量增多,相较于颗粒群边界球体更难发生破碎。
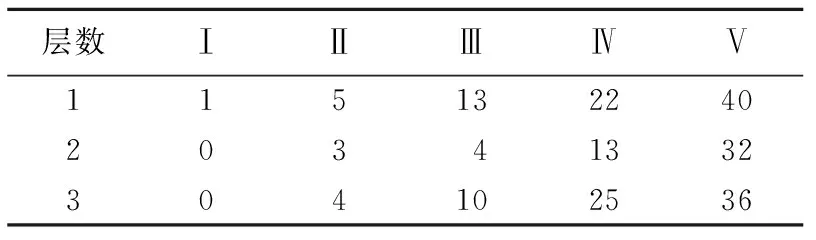
表3 各组试验中每层颗粒破碎数量
对试验Ⅳ和Ⅶ进行比较,试验Ⅶ中发生破碎的试样数量为28,破碎率为23.3%,明显小于试验Ⅳ的50%。这主要是因为有小颗粒填充在大颗粒的空隙中,大颗粒的接触点数显著增加,单个接触点所受法向力相对减小,更不容易发生颗粒破碎现象,因此增加内部颗粒接触点数量可显著减小破碎率。
3 结 论
a.通过拟合,对单点接触条件下球形岩石颗粒接触破碎的锥形核尺寸经验公式进行了修正,使其可适用于多点接触的条件。
b.建立了球形颗粒群高应力条件下破碎率B和竖向荷载P的相关经验公式,并通过试验验证了其有效性,总结了多点接触条件下球形粗粒料颗粒群的破碎规律。
c.同等荷载条件下,增加粗粒料颗粒与周围颗粒接触点的数量可有效降低破碎率。
本文研究了多点接触条件下球形颗粒的破碎特性。但实际工况中,粗粒土颗粒的形状复杂多样,形状的改变对颗粒破碎的影响还需进一步研究。
