碾压混凝土真实应变率效应试验

2022-03-29魏培勇张社荣王枭华

河海大学学报（自然科学版） 2022年2期

魏培勇，张社荣，王枭华，王超

(1.天津大学水利工程仿真与安全国家重点实验室，天津 300350； 2.天津大学建筑工程学院，天津 300350)

近年来，随着恐怖主义、地区冲突加剧，制导导弹、炸弹等导致的爆炸袭击风险不断增加。作为水利枢纽的核心建筑物，水工大坝在极端荷载下一旦失事会对工程本身乃至大坝下游造成不可估量的损失。因此，研究各种爆炸荷载下大坝的损失机制及失效模式至关重要。作为一种特殊的混凝土材料，碾压混凝土因其特殊的配合比和施工成型方式而广泛应用于重力坝和拱坝工程中[1]。为了准确预测碾压混凝土坝在爆炸等极端荷载下的损伤机理和失效模式，亟须建立考虑应变率效应的碾压混凝土动态本构模型，合理评价其应变率关系是进行碾压混凝土坝抗爆性能评价的首要任务。

研究表明，混凝土类材料力学性质具有明显的应变率效应，由应变率效应引致的强度增强通常由动态增强因子(dynamic increase factor，DIF)表征[2-4]，现今许多DIF经验公式被用于工程设计与结构分析中[4-5]。作为一种混凝土材料，碾压混凝土的动态行为也呈现出明显的应变率敏感性，前期已基于碾压成型方式(初始损伤[6]、软弱夹层[7]等)对碾压混凝土动态压缩性能的影响进行了大量研究。

然而，现有DIF公式之间存在较大的差异。除试验条件外，研究表明，惯性和端面摩擦约束导致的结构效应是引起这种差异的重要原因[8-11]。同时，结构效应与试件尺寸密切相关，因此包括碾压混凝土在内的混凝土材料的动态力学行为呈现出与静态荷载下不同的尺寸效应[12-14]。在特定应变率下，动态抗压强度随试件尺寸增大而增强。大尺寸试件具有更显著的应变率敏感性，但较高应变率下力学行为具有更明显的离散性[14]。由此推断，高应变率荷载下的强度增强可归因于材料应变率效应和结构效应。此外，混凝土碎块分形特征可以用于解释结构效应导致的动态抗压强度增量尺寸相关性[15]。

结构效应和真实应变率效应(即材料本身的应变率效应)是引起混凝土类材料DIF增大的主要原因，直接采用分离式Hopkinson压杆(split Hopkinson pressure bar，SHPB)试验获得的DIF描述混凝土类材料必然会高估动态抗压强度增强情况，因此有必要从试验结果中剔除结构效应的影响，避免对应变率效应的高估[16-17]。为了克服这一局限性，学者通过数值模拟、试验和理论解析等方法对SHPB试验中惯性效应进行研究，其中部分研究试图将惯性效应引起的动态抗压强度增量与试验结果解耦。如，Hao等[9]通过数值模拟量化惯性效应对DIF的贡献；Lee等[16]进行了混凝土SHPB试验研究，并基于线弹性理论提出了可描述材料真实应变率敏感性的DIF公式；陈徐东等[18]对冲击弯拉试验中的惯性力进行了讨论，并计算出了试件受到的惯性力。另一方面，试件与压力杆间的端部摩擦约束也会导致混凝土动态抗压强度增强的高估，有关学者提出了端部摩擦约束与应变率、摩擦系数、长径比之间的经验关系[10-11，17，19-20]。在此基础上，将从SHPB试验得到的实测强度中消除了由横向惯性效应和端面摩擦效应引起的动态抗压强度增强量后，即可得到混凝土材料的真实应变率效应，从而更精确地评估材料的动态力学行为。尽管诸多学者已对常态混凝土应变率效应开展了大量试验[21]和数值仿真[22]研究，但是作为一种特殊的混凝土材料，独特的材料组分和成型方式使得碾压混凝土力学性能与常态混凝土不尽相同，且其应变率敏感性与常态混凝土存在一定差异[6-7]。

本文旨在研究消除结构效应(惯性效应和端面摩擦效应)以获得碾压混凝土材料真实的应变率效应。为此，进行了3种不同尺寸的碾压混凝土SHPB试验，通过数值仿真、经验公式及简化理论模型确定了惯性约束与端部摩擦约束引起的动态抗压强度增强，然后将结构效应引起的动态抗压强度增量分别从SHPB试验获得的DIF数据中消除，通过回归分析得到碾压混凝土的真实应变率效应。

1 SHPB试验

1.1 原材料及试样制备

水泥采用祥云P·MH42.5级中热硅酸盐水泥，满足GB/T 200—2017《中热硅酸盐水泥、低热硅酸盐水泥》要求；粉煤灰采用贵州火焰Ⅱ级粉煤灰，满足GB/T 1596—2017《用于水泥和混凝土中的粉煤灰》要求；水胶比为0.50，其中粉煤灰占胶凝材料质量分数的60%；粗骨料采用人工碎石，最大粒径为19 mm，其原岩单轴抗压强度为82.0 MPa；减水剂采用JM-Ⅱ型缓凝高效减水剂，减水率为24.5%；引气剂采用HLAE型引气剂，含气量为5.4%。水泥、粉煤灰、水、砂、大石、中石、小石、减水剂和引气剂的质量比例为70∶106∶88∶672∶452∶452∶603∶1.408∶0.088。

碾压混凝土成型时模拟了现场施工中分层碾压施工工艺。使用DC-25C手持式振动碾对碾压混凝土拌合物进行分层碾压，层厚为10 cm，共计5层。成型后的碾压混凝土在标准养护条件下养护90 d，随后经过钻芯取样、切割打磨等流程最终得到3种不同尺寸(∅50 mm×25 mm、∅75mm×37.5 mm、∅100 mm×50 mm)的碾压混凝土试件。试件制备流程见图1。需要注意的是，试件尺寸相较于骨料最大粒径偏小，可能影响试件材料的均匀性，同时钻芯、切割和打磨等制备流程会给试件表面带来一定初始损伤，这些问题有可能影响SHPB冲击试验结果的离散程度。

图1 碾压混凝土试样制备流程示意图Fig.1 The preparation procedures for different dimensional RCC specimens

1.2 试验设计

采用3种不同压杆直径(50 mm、75 mm、100 mm)的SHPB装置分别对不同尺寸的试件进行冲击压缩试验。试验方案编号见表1。试验采用4种气压研究各尺寸试件动态压缩性能；通过脉冲整形技术修正入射波形，以确保近似恒定应变率加载以及试样中的应力均匀性。同时，对碾压混凝土进行准静态单轴压缩试验以确定其单轴抗压强度。

表1 碾压混凝土试验方案编号

1.3 有效性验证

基于一维应力波理论、平面假设和均匀性假设，试验可从入射杆和透射杆上的应变片测得入射、反射、透射应变脉冲。由式(1)～(3)计算试件的平均应变ε(t)、应力σ(t)和应变率历史，图2(a)为试验中获得的典型应力时程关系曲线。

σ(t)=EbAb[εi(t)+εr(t)+εt(t)]/(2As)

(1)

(2)

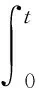
(3)

式中：cb为压力杆纵向弹性波速；Eb为压力杆弹性模量；Ab为压力杆横截面面积，εi(t)为入射应变脉冲；εr(t)为反射应变脉冲；εt(t)为透射应变脉冲；As为试件横截面积；ls为试件长度。

图2(c)(d)为不同尺寸试件的典型应力-应变关系曲线及应变率-应变曲线。试件前、后端面应力分别为

σf(t)=AbEb[εi(t)+εr(t)]/Asσr(t)=AbEbεt(t)/As

(4)

图2(c)(d)中各尺寸试件前后端面应力-应变曲线很接近(即εi(t)+εr(t)≈εt(t))，可认为试验中试件内部应力满足均匀性假设，因此试验有效。对式(1)～(3)进行简化并用于碾压混凝土动态力学特性计算。另一方面，应变率-应变曲线均存在一个相对平稳的阶段，说明通过合理运用脉冲整形技术可以实现恒定应变率加载。

2 RCC动态抗压强度的尺寸效应

研究表明，混凝土类材料的动态抗压强度受结构效应的影响，同时，大尺寸试件表现出更明显的应变率敏感性，与尺寸相关的强度增强呈现出非线性的特点[14]，然而尺寸相关的结构效应不能准确反映真实的材料应变率效应。表2为不同尺寸试件在近似应变率下(约70/s)的动态抗压强度，其中碾压混凝土试件(∅100 mm×200 mm)单轴抗压强度为10.17 MPa。由表2可知，相同应变率下碾压混凝土试件的动态抗压强度均值随试件尺寸的增大而明显增强。

表2 相近应变率下不同尺寸RCC试件动态抗压强度

图3(a)更直观地展示了结构效应导致的动态抗压强度尺寸效应。碾压混凝土动态抗压强度具有明显的应变率敏感性和尺寸效应，此外动态抗压强度增量也随应变率增长而变大。将包含结构效应影响的动态抗压强度增强定义为表观DIF，即SHPB试验中获得的动态抗压强度与单轴抗压强度的比值。图3(b)为不同尺寸试件表观DIF与应变率之间的关系。由图3可知，采用表观DIF进行结构分析很可能会过高估计其动态抗压强度，进而得到不保守的结果。此外，较高的强度变化幅度有可能导致应变率关系的错误评估。因此，有必要将结构效应从表观DIF中消除从而得到碾压混凝土的真实应变率效应。

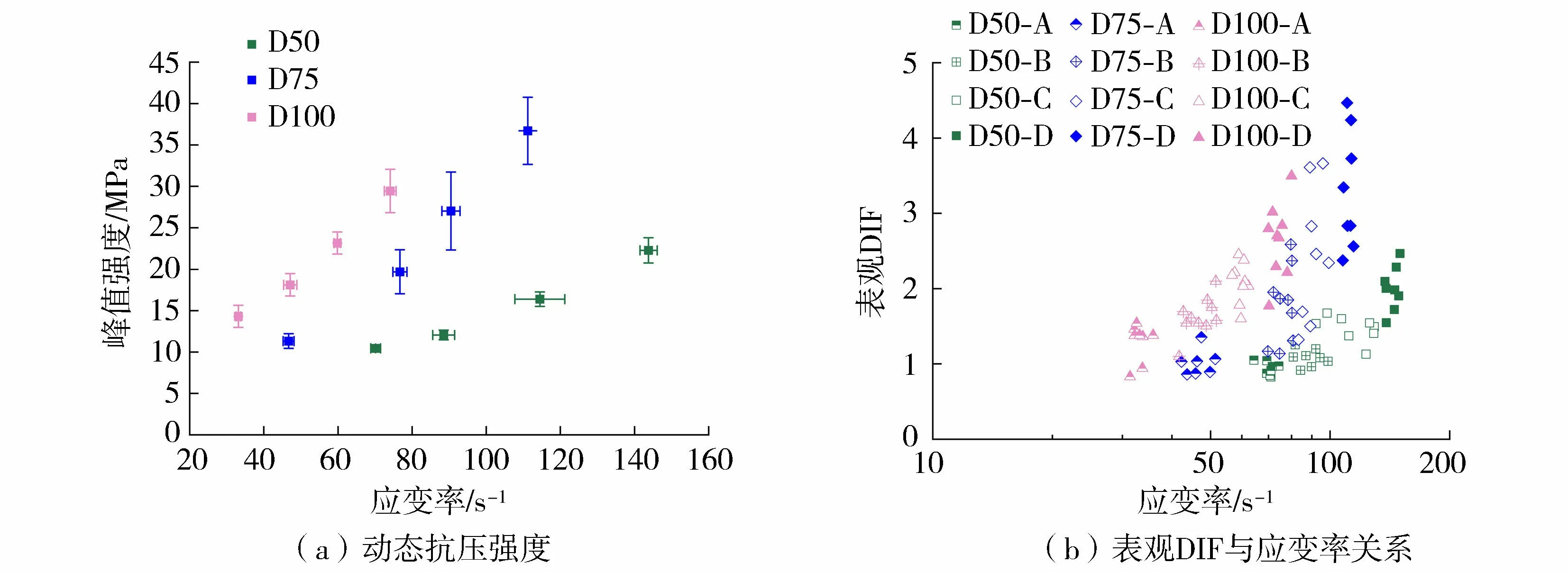
图3 不同尺寸RCC寸试件SHPB试验结果Fig.3 SHPB test results for different dimensional RCC specimens

3 真实应变率推导

研究表明，混凝土类材料的动态抗压强度增强主要由横向惯性效应、端面摩擦效应和真实应变率效应引起。如果直接使用由SHPB试验得到的DIF数据，相应的混凝土动态抗压强度会被高估。假定真实应变率效应、横向惯性效应和端面摩擦效应互不相关[23-24]，则材料的动态抗压强度增强表达见式(4)，真实应变率效应可通过数值模拟等方法消除端面摩擦和横向惯性效应的贡献得到。

(5)

3.1 SHPB试验数值模拟方法

为研究横向惯性效应对SHPB试验的影响，建立如图4(a)所示的简化均质数值仿真模型以模拟SHPB试验，混凝土试件和杆的网格尺寸分别控制在0.5 mm和3.0 mm。此外，采用关键字CONTACT_SURFACE_TO_SURFACE模拟试件和杆之间的摩擦。

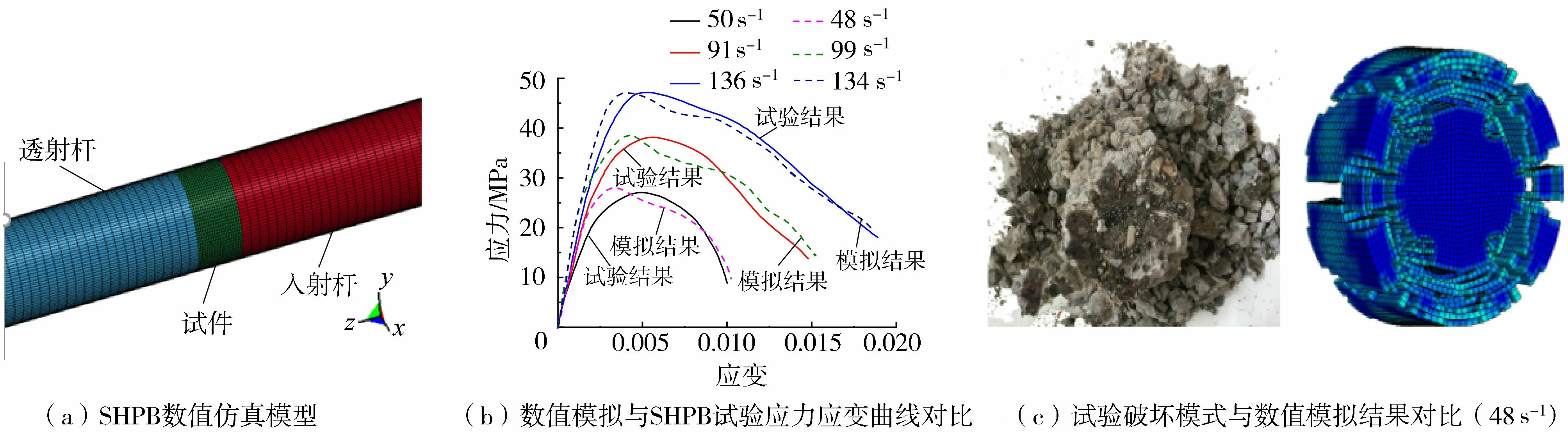
图4 数值模型及验证Fig.4 Numerical model and verification

选用KCC本构(MAT_072R3)模拟碾压混凝土动态荷载下的力学响应。对于KCC本构，仅需输入关键参数(例ρs=2 230 kg/m3，fc=11.13 MPa)，剩余参数可自动生成。入射杆和透射杆采用均质线弹性本构(MAT_1)，数值模拟中各材料本构及其参数见表3。

表3 数值仿真中材料本构及其参数

在入射杆前端面施加SHPB试验测得的半正弦应力波形，采用关键字MAT_ADD_EROSION中的最大失效主应变控制RCC单元失效与删除，数值模型其他设置参考文献[25]。如图4(b)(c)所示，相同应变率下数值模拟结果与SHPB试验得到的应力应变曲线吻合良好，验证了数值模型的合理性。

3.2 表观DIF数据解耦分析

3.2.1 端面摩擦效应对DIF值的影响

试件-杆接触面的端面摩擦会在一定程度上限制试件的横向变形，进而影响SHPB的试验结果。因此，端面摩擦引起的动态抗压强度增强不可忽视。Hao等[10-11]对SHPB试验进行了细观仿真，并研究了端面摩擦等因素对动态力学性能的影响，结果表明端面摩擦引起的动态抗压强度受长细比、摩擦系数及应变率的影响。此外，为了量化端面摩擦对动态抗压强度的影响提出了相应的经验公式：

(6)

Δfμ=(1-χ)fd

(7)

式中：Iμ>0为考虑端面摩擦效应的DIF值；Iμ=0为不考虑端面摩擦效应的DIF值；χ为Iμ>0和Iμ=0的比值。

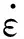
图5 不同尺寸试件SHPB试验结果Fig.5 SHPB test results for different dimensional RCC specimens

3.2.2 横向惯性效应对DIF值影响

为了准确评估碾压混凝土的真实应变率效应，消除表观DIF中惯性效应的影响尤为重要。从SHPB试验中获得的表观动态增强因子可表述如下：

Is=fd/fc=(fc+Δfi+Δfμ)/fc

(8)

式中：Is为横向惯性效应和端面摩擦效应引起的动态抗压强度增长因子。

Δfi=(Is-1)fc-Δfμ

(9)

定义惯性效应贡献率为(fi/(Iafc))，数值模拟获得的惯性效应贡献率与试件尺寸、应变率间的关系曲线见图6(a)。相应地，图6(b)为不同尺寸试件不同应变率荷载作用下因惯性效应引起的强度增量。由图6可知，碾压混凝土动态抗压强度的惯性效应具有应变率敏感性和尺寸相关性，更高应变率或更大试件尺寸会导致惯性效应的增强。

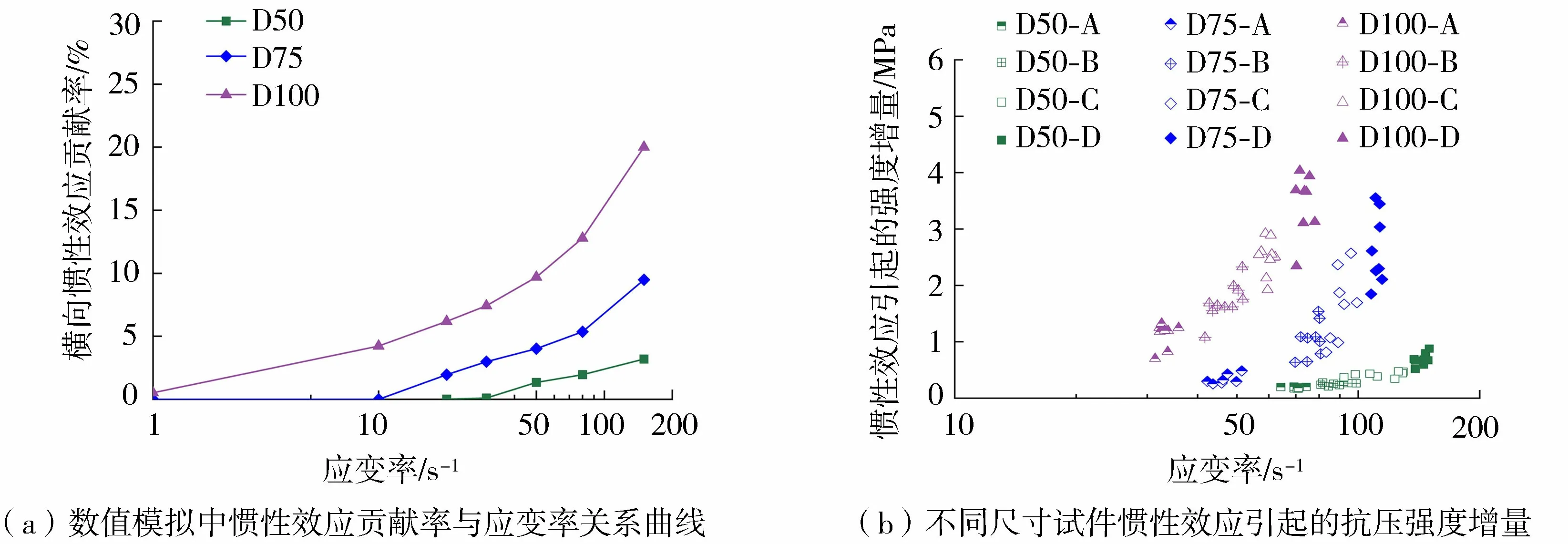
图6 惯性效应引起的强度增量Fig.6 Strength enhancement from inertial effect

3.3 碾压混凝土真实应变率效应

由SHPB试验直接获得的DIF数据是横向惯性效应、端面摩擦效应和材料真实应变率效应共同作用的结果。将量化的端面摩擦效应和横向惯性效应导致的动态抗压强度增量从SHPB试验直接获得的DIF数据中消除后得到真实应变率效应：

(10)

根据式(10)可得反映碾压混凝土真实应变率效应的修正后DIF数据，如图7(a)所示。式(11)广泛用于描述岩石、混凝土等准脆性材料的应变率效应[3]，本文采用式(11)拟合真实动态强度增强与应变率之间的关系:

(11)

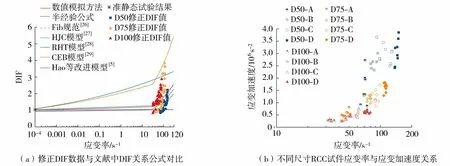
图7 碾压混凝土真实应变率效应Fig.7 True strain rate effect of RCC

采用最小二乘法对图7(a)中修正的DIF数据进行拟合，确定式(11)中参数k0=0.015，k1=0.017。图7(a)对本文提出的碾压混凝土真实应变率关系与现有经典模型[5，26-29]进行了比较。由图7可知，尽管由于碾压混凝土成型工艺导致修正后的DIF数据仍具有一定的离散性，本文提出的碾压混凝土真实应变率关系曲线与Fib规范[26]和HAO等[5]提出的DIF关系较为接近，进一步验证了结果的合理性。

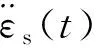
(12)

(13)

式中：k2为横向惯性效应的率相关参数；k3为轴向惯性效应的率相关参数。

将式(5)和式(12)代入式(10)中，非负边界条件下可采用最小二乘法拟合得到方程各参数：k1=0.015 0，k2=0.263 3，k3=0.065 8。同时，为保证应变率效应的连续性，取k0=5.177×10-3。通过消除惯性约束和端面摩擦约束带来的动态抗压强度增强，可以由半理论公式推导出碾压混凝土的真实应变率效应。由图7(a)可知，与数值模拟拟合曲线相比，半理论公式推导得到的真实应变率效应相对较弱，但是高应变率下二者均落在Fib规范[26]和Hao等[5]提出的应变率效应范围内。