高阶Boussinesq型水波方程色散和变浅性能的改进

张振伟，刘必劲，邹志利，傅丹娟

(1.厦门理工学院土木工程与建筑学院，福建 厦门 361024 ； 2.海南浙江大学研究院，海南 三亚 572025；3.大连理工大学海岸和近海工程国家重点实验室，辽宁 大连 116024)

波浪在近岸区域的传播运动是海岸动力学研究的重要内容之一，也是研究近岸环流、海岸演变等的基础。波浪传播运动过程中因受地形影响会产生折射、绕射、反射等物理现象。Boussinesq[1]在研究浅水波运动时建立了一维平底非线性Boussinesq方程；Peregrine[2]推导建立了适用于非平底的经典二维Boussinesq方程；Abbott等[3]首次应用Peregrine方程建立了二维Boussinesq方程计算模型，研究了港口内波浪传播运动；Witting[4]针对经典Boussinesq方程存在的缺点，提出了Boussinesq型方程的适用范围。Madsen等[5-6]建立了二阶色散精度的Boussinesq方程，因该形式的方程具有一定精度且计算量相对较小，在实际中得到了一定的应用[7-8]。此后，许多学者不断对Boussinesq型方程进行改进[9-16]，进一步提高了方程的适用范围。国内有关学者也开展了Boussinesq型方程发展及应用的研究。张尧等[17]综述了Boussinesq型方程的理论发展、实际应用和理论瓶颈，提出了Boussinesq型方程可能的科学突破方向。孙家文等[18]对1967—2018年Boussinesq型方程的理论研究进行了综述，将Boussinesq型方程进一步分为水平二维和三维两种情况。刘必劲等[19]应用简化的双层Boussinesq模型研究了聚焦波波面位移、波面处的水平速度和垂向速度，结果显示模型计算结果与试验测量结果符合很好。

Boussinesq型方程色散参数是通过分析方程色散关系与线性波理论色散关系的Padé展开给出的，而后通过线性变浅分析得到变浅参数。刘忠波等[20-22]针对Madsen等[10]提出的一组四阶Boussinesq型方程，注意到色散参数取值不同可以影响方程的色散精度，于是使方程相速度与线性波相速度在无因次水深kh=15内误差平方累计之和最小以优化色散参数，计算表明这一方法可以显著提高色散适用范围；同时对四阶Boussinesq型方程变浅系数重新进行了优化，优化后的参数显著提高了方程的色散性；另外通过引入含参数的变换速度变量取代原方程中的速度变量，对3组著名的Boussinesq型方程[9，10，13]进行了改进，显著提高了方程的变浅性能。Simarro等[23]对一些经典的Boussinesq型方程[10，13，24]进行了参数优化，参数优化后的方程控制了线性波的波幅误差，变浅性能得到了改善。

文献[11]的Boussinesq型方程是具有四阶色散精度的水平二维方程，方程最高空间导数为三阶，对数值计算要求相对较低。目前，工程上应用最广的是二阶Boussinesq型方程[7-8]，随着计算能力的提高，四阶Boussinesq型方程必将在实际工程中得到应用。另一方面，没有针对文献[11]中Boussinesq型方程参数优化的相关研究，这里不注重提高文献[11]中方程的适用水深范围，而是保持原方程的适用水深范围内，通过优化参数提高方程模拟近岸水波运动的精度。本文在无因次水深kh=6.28条件下，将文献[11]中Boussinesq型方程的相速度与线性波相速度之间误差平方累计之和最小以优化方程色散参数，而后根据变浅分析确定变浅参数，并分析了不同参数对方程色散和变浅性能的影响。最后通过数值模拟潜堤上波浪运动变形问题来验证该方法的合理、有效性。

1 Boussinesq水波方程及其数值模型

1.1 Boussinesq水波方程

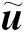
(1)

其中μ=kh

最终方程如下：

(2)

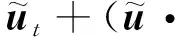
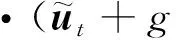
(3)

其中d=h+ηa=a1+a2b=b1+b2c=c1+c2

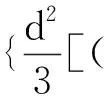
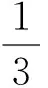
式中：k为波数；h为水深；a、b、c为待定参数；h为静水水深；η为波面升高；d为总水深。

为使方程具有较好的色散和变浅作用性能，文献[11]通过将方程色散关系与线性Stokes色散关系的Padé四阶逼近一致得到色散参数，而后应用变浅性能的优化得到变浅参数，最终参数(a1，a2，b1，b2，c1，c2)=(-0.006 7，-0.022 0，-0.001 7，0.000 5，0.039 3，0.061 3)。刘忠波[16]开发了六参数Boussinesq型方程的计算程序，应用六参数方程开展了潜堤上波浪传播运动的模拟研究，在其计算程序中六参数取值为(a1，a2，b1，b2，c1，c2)=(-0.006 645 873，-0.022，-0.001 691，0.000 547，0.039 291，0.061 3)，与文献[11]相比，文献[16]中的部分参数保留了更多的有效数字。经重新计算和确认，这与文献[16]中Luth等[26]算例采用的参数是一致的。

六参数方程的色散关系表达式、Stokes线性色散关系的Padé四阶逼近表达式分别为

(4)

ω2=gks2h[1+1/9(ksh)2+1/945(ksh)4][1+4/9(ksh)2+1/63(ksh)4]-1

(5)

式中ks为Stokes线性波波数。

采用文献[20]中的方法对六参数方程的色散性参数进行改进。对于从深水传播到近岸浅水的波浪，当波浪传播到近岸之后kh值不断减小，取kh=6.28可以使方程考虑从深水到浅水的波浪传播过程，即在kh≤6.28时，保证方程相速度与线性波相速度之间误差平方累计之和最小。由此可以得到(a，b，c)= (-0.024 494 62，-0.000 764 2，0.095 389)。

图1为不同参数的无因次相速度(cs为Stokes线性波相速度，c为Boussinesq型方程的相速度)对比。由图1可见，kh=6.28时，最新优化参数、文献[11]参数及文献[16]参数的色散误差分别为0.069%、5.21%和3.09%。由此可知，优化参数可以较大地提高波浪相速度的模拟精度。

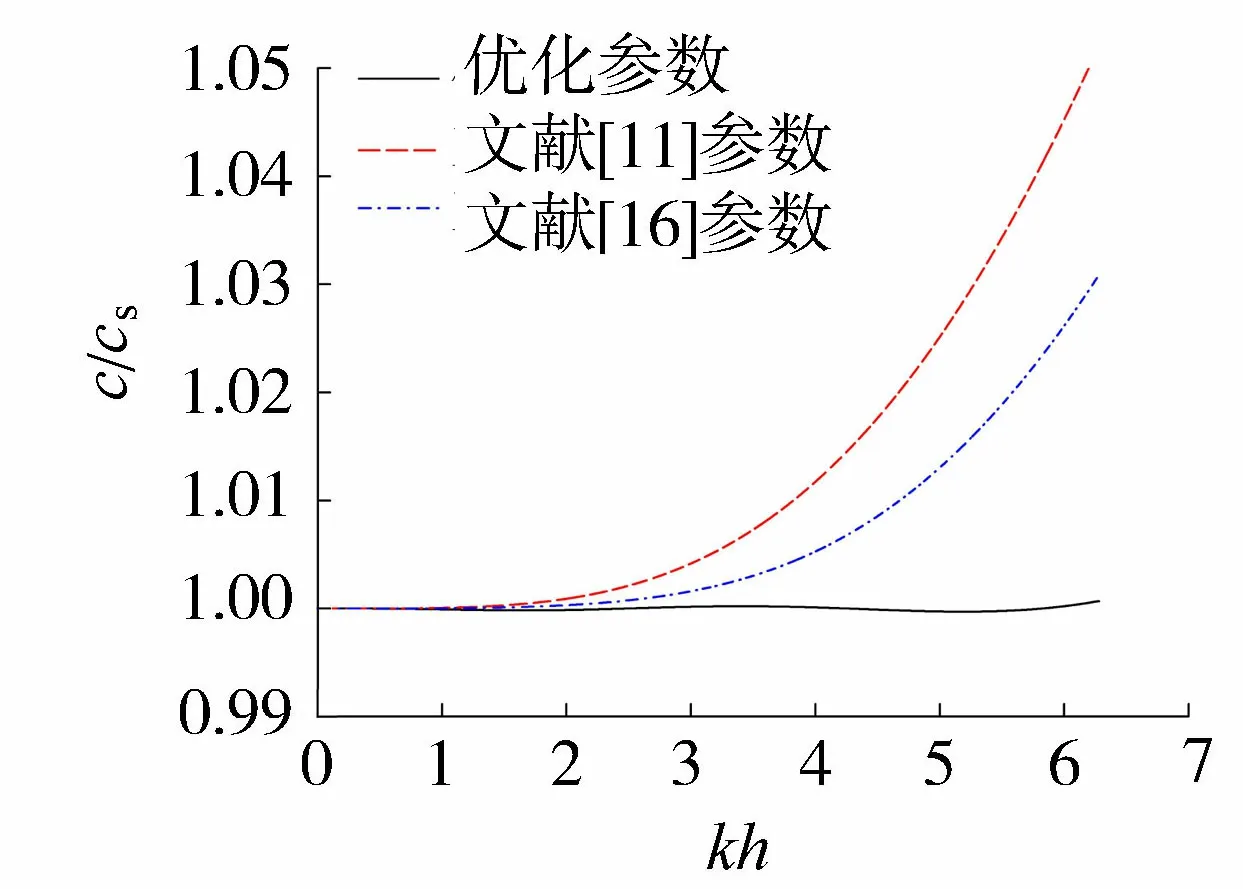
图1 无因次相速度比较Fig.1 Non-dimensional wave phase celerity comparisons

1.2 变浅性能分析

忽略方程的非线性项、(hx)2和hxx项，一维方程可写成：

(6)

(7)

其中γ1=-b/aλ1=-(a+b/a)λ2=-(3a+5b/a+2a2+2b2/a)

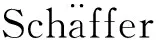
η=A(x)exp[i(ωt-kx)]u=U(x)(1+iσhx)exp[i(ωt-kx)]

(8)

式中：A(x)为波幅；U(x)为速度振幅；ω为频率；σ为考虑地形变化的小变量参数。将式(8)代入式(6)和式(7)并分离实部和虚部，可得关系式：

h(Ux+σkhxU)+γ1h2(2ωkAx+ωkxA)+λ1h3(-3k2Ux-3kkxU-σk3hxU)+

hx(U-λ2k2h2U+γ2ωkhA)=0

(9)

ωA-khU-γ1h2ωk2A+λ1k3h3U=0

(10)

-ωσhxU+λ3ωh2(2kUx+kxU+σk2hxU)+gAx+3cgh2(k2Ax+kkxA)+

hhx(4c2gk2A+λ4ωkU)=0

(11)

ωU-λ3ωk2h2U-gkA-cgk3h2A=0

(12)

式(10)和式(12)存在非零解的条件是A和U的系数矩阵行列式为0，可以得到六参数方程的色散关系。而后应用式(9)和式(11)推导得到变浅梯度的表达式。将Stokes线性波变浅系数与六参数方程的均方差从0至6.28积分，通过积分误差最小确定变浅系数，由此可以得到六参数方程的6个参数(a1，a2，b1，b2，c1，c2)=(0.003 605 38，-0.028 1，-0.000 764 3，0.0，0.029 389，0.066 0)，线性变浅的详细过程可以参看文献[21，27]。kh=6.28时，最新优化参数变浅与理论值偏差为0.008 4，较文献[11]有了较大提高。

图2为不同参数计算得到的变浅梯度。由图2可见，优化参数给出的变浅梯度在kh为0～6.28的范围内与理论变浅符合较好。为进一步分析参数对方程变浅性能的影响，应用不同参数模拟了线性波在斜坡上的传播运动：地形坡度为19∶600，斜坡深水水深10 m，另一端水深0.5 m，波浪周期为3.581 s，入射波高为0.1 m，kh=3.14、0.407。模拟时，去掉方程所有的非线性项，空间步长为0.05 m，时间步长dt=0.05 s，图3为优化参数、文献[16]参数和文献[11]参数的计算结果，由图3可知，优化参数给出的结果最好，其次是文献[16]参数，再次是文献[11]参数，这从线性变浅的数值方面证明了优化参数可以更好地模拟波浪传播运动。

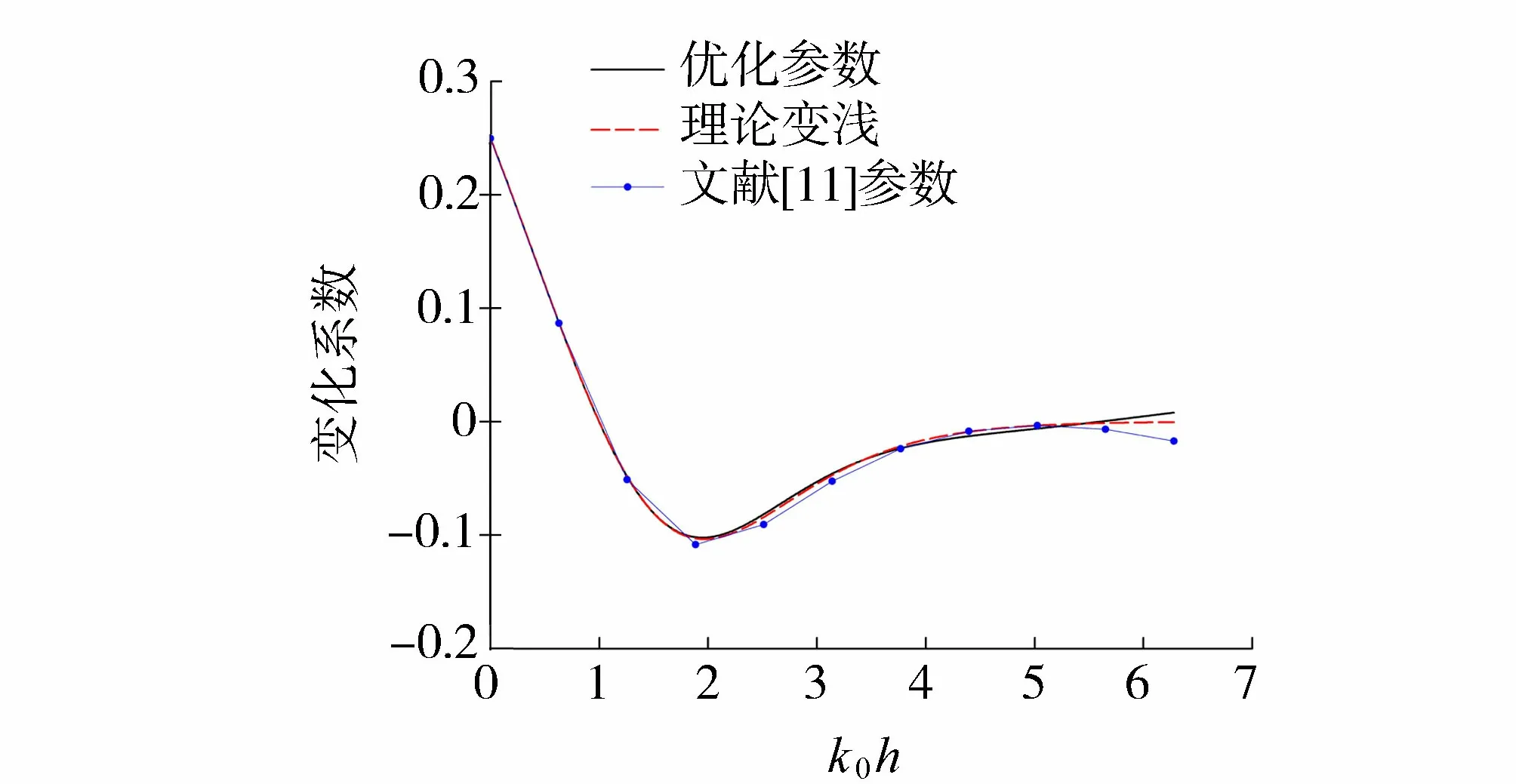
图2 不同参数的变浅梯度系数Fig.2 Linear shoaling gradient for different paramerers

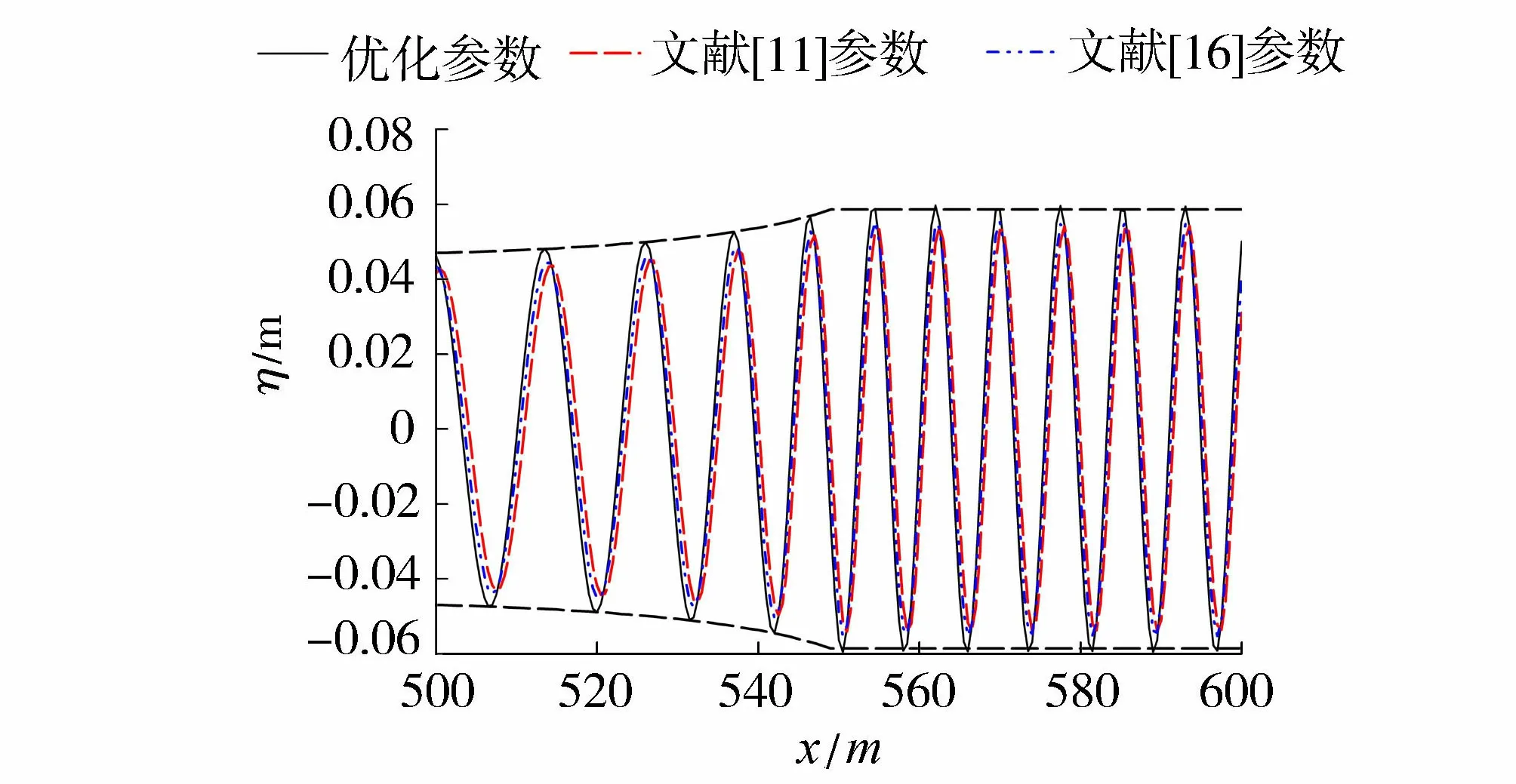
图3 波浪在斜坡上的变浅Fig.3 Wave shoaling along the slope

为了更详细地研究参数的影响，分析六参数方程的二阶谐波波幅，并将其与二阶Stokes波二阶波幅进行比较。利用Madsen等[10]给出的方法进一步考察参数的影响。

η=A1cosθ+εA2cos2θu=U1cosθ+εU2cos2θ

(13)

其中θ=ωt-kx

式中：A1、A2分别为一阶和二阶振幅；U1、U2分别为一阶和二阶速度振幅。

将式(13)代入式(1)和式(2)，分析ε的一阶问题,则可以得到二阶谐波的波幅，二阶谐波方程为

(14)

其中

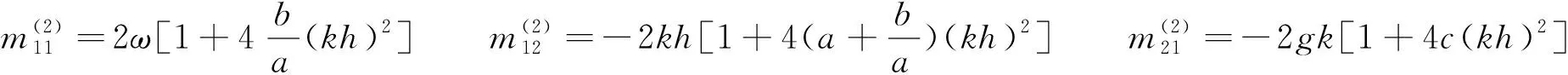
由式(14)可求得A2：

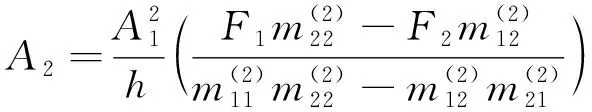
(15)

相应的Stokes二阶非线性解二阶谐波振幅为

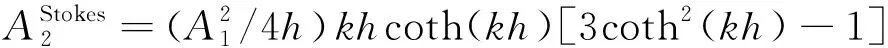
(16)

图4为六参数方程中不同参数对应的二阶谐波波幅对比。从图4可见，优化参数对二阶谐波基本没有改善。Kennedy等[28]指出，方程参数优化使方程线性性能在某一相对水深范围内是可以接受的，但非线性误差随着相对水深的增加而快速变大。本文仅优化了方程的色散和变浅参数，提高了方程的线性性能，没有改进方程的非线性性能，所以二阶非线性基本没有得到改善。

图4 方程的二阶谐波波幅与二阶Stokes波幅的比值Fig.4 Ratio of second order hammonic wave amplitude to second order stokes wave amplitude of equation

1.3 数值方法

六参数方程求解时时间差分为四阶Adams-Bashforth-Moulton混合格式，空间差分为中心差分格式对式和式进行求解。预报时采用3阶Adams-Bashforth预报格式计算式和式中波面和速度的预报值，然后利用4阶Adams-Moulton时间步进格式，计算方程波面和速度的校正值。当变量的校正值与预报值之间的误差小于等于0.000 1时，迭代终止。若不满足迭代终止条件则用校正值和预报值的加权作为变量的新预报值，预报值和校正值的加权系数分别取0.05～0.1和0.95～0.90，可以不断重复校正，直至满足条件为止[16]。在数值模拟时，采用内部造波法产生波浪，波浪产生位置与模型试验中造波机的位置一致，另外在计算域的左端和右端设置2倍波长的海绵层吸收波浪，阻止反射波的产生。

2 算 例

采用六参数方程数值模型，针对潜堤存在时波浪的传播运动进行数值模拟，并与试验的测量结果进行了比较，给出了采用不同参数的计算结果。

Luth等[26]和Ohyama等[29]分别进行了梯形潜堤上波浪传播变形试验，试验布置见图5。表1为Luth等[26]试验和Ohyama等[29]试验的入射波浪要素，数值计算中空间步长取0.025 m，时间步长取0.005 s，数值波浪水槽长55 m。

图5 Luth等[26]和Ohyama等[29]试验布置(单位：m)Fig.5 Experiments setup of Luth et al. and Ohyama et al. (Unit：m)

表1 Luth等[26]试验和Ohyama等[29]试验波浪要素

图6和图7分别为Luth等[26]试验数值计算的波面升高与实测数据的对比。由图6的计算结果可以看出，从x=2.0 m到x=14.5 m，采用3组参数计算得到的波面升高差别不大，但从x=15.7 m之后，采用3组参数计算得到的波面升高的差别显现出来。采用本文优化参数的计算结果略好于采用文献[16]参数的计算结果。采用文献[11]参数计算的结果最差，这一点可以从x=17.3 m到x=21.0 m波面升高的计算结果看出来，波浪经过潜堤时，不同频次的锁相波被释放成为自由波，波面时间过程线会出现多种形态的次峰。若方程的色散性能较好，则可以较为准确地捕捉到各个锁相波的位置，而方程变浅性能好则可以较准确地模拟波浪在斜坡上运动的波高演化。在x=19.0 m处，采用本文优化参数计算的结果与波面升高符合最好，其次是采用文献[16]计算的结果，采用文献[11]参数计算得到的波面升高最差。

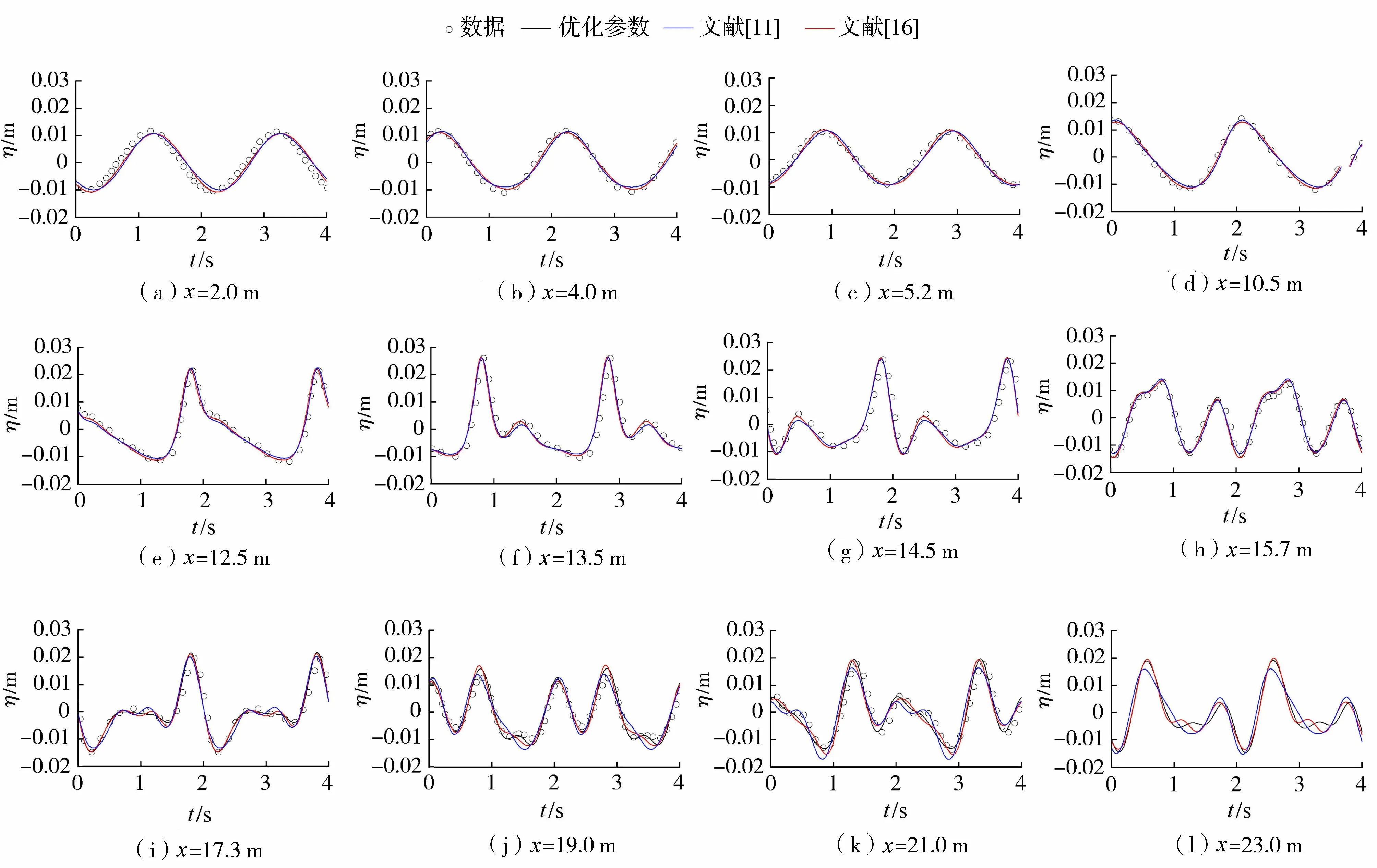
图6 不同浪高仪处数值模拟结果与试验数据的对比(Luth等[26]试验算例(a))Fig.6 Comparisons between the computed results and experimental data at different locations(Luth et al.[26] experiment example(a))

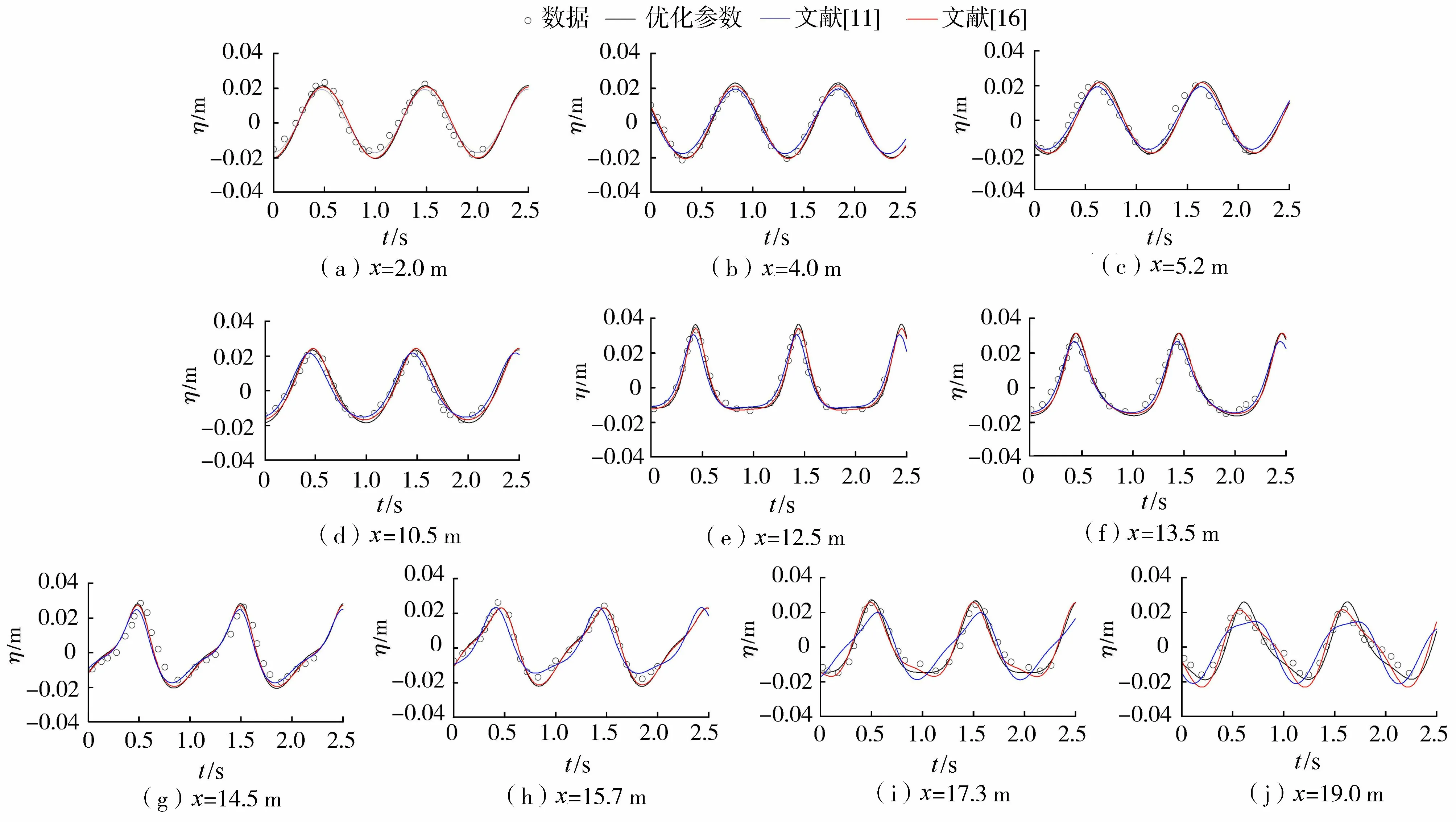
图7 不同浪高仪处数值模拟结果与试验数据的对比(Luth等[26]试验算例(c))Fig.7 Comparisons between the computed results and experimental data at different locations(Luth et al.[26] experiment example(c))

图7为Luth等[26]试验算例(c)的计算结果。由图7可知，自x=2.0 m到x=19.0 m，采用3组参数计算的结果存在明显差别，这是由于该算例对方程的色散性能要求较高。因文献[11]参数的色散性最差，文献[16]参数的色散性稍好，采用本文优化参数的Boussinesq型方程的色散性最好。特别是越过潜堤之后(x=14.5 m至x=19.0 m)，采用文献[11]参数计算结果与试验结果差别最大，采用本文优化的参数与文献[16]参数计算的结果偏差相对较小，总体上采用本文参数波面升高的计算结果与试验数据符合最好。

图8为Ohyama等[29]试验波面升高计算结果与试验结果的对比。由Ohyama等[29]试验的入射波要素说明3组试验的非线性参数一致，色散性参数不一致，其中算例(2)的色散性参数最大。图8给出了3号浪高仪和5号浪高仪位置处的波面升高计算结果与试验结果的对比。由图8可以看出，对于算例(2)，本文优化参数所得的计算结果明显优于采用文献[11]和文献[16]参数的计算结果。在5号浪高仪位置处，3组参数给出的计算结果差别最大，采用文献[11]参数的计算结果与试验数据各个谐波的相位不相符合。对于3号浪高仪，随着试验工况波浪色散性参数的减小，采用3组参数计算的结果差别也会变小。算例(6)3号浪高仪处的计算结果差别最小，这一点在5号浪高仪处也有体现，即随着试验波况色散性参数的降低，采用3组参数给出的计算结果差别变小。

图8 不同浪高仪处数值模拟结果与试验数据的对比(Ohyama等[29]试验)Fig.8 Comparisons between the computed results and experimental data at different locations(Ohyama et al.[29] experiment )

3 结 论

a.通过优化方程的参数，可以提高方程的色散性。在kh=6.28时，本文优化参数、文献[11]参数及文献[16]参数给出的色散性误差分别为0.069%、5.21%和3.09%，可见本文优化参数显著提高了六参数方程的色散性。参数对Boussinesq型方程计算结果影响很大，因此在给出参数时要保留足够的有效数字。变浅参数优化后，当kh=6.28时，最新优化参数变浅与理论值偏差为0.008 4，精度也有了提高。线性变浅的计算表明，采用本文优化参数的Boussinesq型方程变浅性能得到了提高。二阶谐波分析表明，优化参数对二阶谐波基本没有改善。二阶非线性性能的提高需要对方程的非线性进行改进。

b.采用3组参数针对潜堤上波浪的传播变形进行了计算研究，结果表明采用本文优化参数给出的计算结果与试验数据更为符合，这也进一步说明参数对方程色散和变浅的重要性。