横流环境下振荡射流三维数值模拟

2022-03-29徐振山陈永平

河海大学学报（自然科学版） 2022年2期

李蒙，徐振山，陈永平

(河海大学港口海岸与近海工程学院，江苏南京 210098)

废水(如达标废水、浓盐水、温排水)向河流和海洋的排放是环境水力学和排放工程关注的重点问题。陆源废水通常以射流的形式排放到受纳水体中，排放过程可划分为排放近区的初始稀释过程和排放远区的后续稀释过程。Zhao等[1]认为废水在排放近区的初始稀释度将决定排放远区污染物的影响范围。因此，研究废水在排放近区初始稀释度具有现实意义。

定常排放的非振荡射流是目前废水排放的主要形式。Kelso等[2]发现，与静水环境中射流相比，横流环境中的非振荡射流轴线流速衰减明显加快，拓展宽度大大增加。Sau等[3-4]学者总结出非振荡射流4种典型的涡动结构为剪切层涡、马蹄形涡、反向对称漩涡(CVP)和尾涡，其中CVP结构是横流环境中非振荡射流最为重要的特征之一。Plesniak等[5-6]发现射流-横流速度比是影响非振荡射流运动和扩散特性的主要因素。

在排放近区，除受纳水体的动力外，射流本身的参数如射流水体速度、密度、排放角度也会对初始稀释过程产生影响。正弦振荡射流的研究近几年来有了一定的进展。Hsu等[7-8]采用粒子图像测速技术(PIV)对横流环境中正弦振荡射流的流场进行测量，将一个周期内射流的运动过程划分为4个典型模式：下冲模式、恒定流主导模式、射流主导模式和过渡模式。Marcum等[9-10]通过室内物理试验分析了射流振荡幅度和频率对横流-射流相互作用的影响，认为可通过调节射流振幅和频率来增大射流与周围流体的掺混和卷吸。波流环境中的非振荡射流与横流环境中的振荡射流有着类似之处。徐振山等[11-12]建立了波流共同作用下非振荡射流的三维数学模型，并系统分析了非振荡射流的三维流场结构，发现表征射流最主要特征的CVP结构发生了较大改变，非振荡射流与周围水体的掺混大大增加，其扩展宽度也明显增加。张玉玲等[13]与丁宏伟等[14]分别进行了波流环境中多孔射流与双孔浮射流的研究，其相关结果可以为振荡射流的研究提供参考。

截至目前，关于横流环境中正弦振荡射流的研究还局限于二维层面，三维的运动特性和稀释规律仍需进一步研究。本文采用大涡数学模型对横流环境下的正弦振荡射流进行模拟，研究振荡射流在横流环境下的运动特性和稀释规律，探讨振荡参数对射流的影响。

1 数学模型简介

1.1 LES控制方程和数值算法

大涡数值模拟(large-eddy-simulation，LES)的控制方程为空间平均的N-S方程和标量输运方程：

(1)

(2)

(3)

式中：xi(i=1，2，3) 为笛卡尔坐标系统中的x、y、z；ui(i=1，2，3)为xi方向的瞬时速度分量u、v、w；ρ为密度；p为瞬时静水压强；v为运动黏滞系数；gi为重力加速度；τij,SGS为亚格子剪应力；c为浓度标量；Γ为分子扩散系数；qi,SGS为标量亚格子紊流通量；Pr为分子Prandtl数。

τij,SGS可分为各向异性的偏斜部分τij和各向同性的对角部分τkk,SGS，τkk,SGS可与压力项合并求解。应力张量τij采用Smagorinsky模型[15]模拟表示为

(4)

(5)

式中：Sij为对称变形速度梯度张量；νt为涡黏性系数；Cs为Smagorinsky常数，一般取值为0.12～0.28，根据张玉玲[16]模拟率定可得Cs=0.175时更符合实际情况；Δ为滤波尺度，表示为Δ=(Δx1Δx2Δx3)1/3，Δx1=Δx、Δx2=Δy、Δx3=Δz分别为x、y和z方向上的空间步长。

采用有限差分法中的分裂算子法求解控制方程，计算过程主要分为3步：第一步求解动量方程中的对流项，采用二次向后特征线法和 Lax-Wendroff格式平均法对对流项进行离散求解以提高计算精度；第二步采用时间前差、空间中心差分格式离散求解扩散项；第三步采用投影法对压力传播项中的压力和速度进行耦合求解，并更新自由表面。

1.2 模型边界条件

数值计算采用合成涡法(synthetic-eddy-method，SEM)生成振荡射流边界条件，并将得到的振荡射流植入数值水槽中进行模拟。底部采用可滑移边界预测第一个网格节点的速度梯度，采用壁面函数法计算底部切应力。侧向边界采用不可入边界条件。

2 模型验证与模拟工况

2.1 横流环境中射流验证

采用一组横流环境中非振荡射流的数据对模型速度与浓度结果进行验证，具体参数如下：试验水深h=0.5 m，非振荡射流平均速度w0=1.22 m/s，射流雷诺数Re=12 200，水流流速u0=0.133 m/s。

图1与图2分别为不同下游断面上射流时均垂向速度、浓度沿水深分布数值模拟结果与实测数据对比。在射流主体区域数值模拟结果与实测数据吻合较好，试验数据与数值模拟结果误差在可接受范围内。针对该模型的更多验证参见文献[17]。

图1 不同下游断面上射流时均垂向速度数值模拟结果与试验数据对比Fig.1 Comparison of numerical simulation results and experimental data of jet time-averaged vertical velocity on different downstream cross sections

图2 不同下游断面上射流时均浓度数值模拟结果与试验数据对比Fig.2 Comparison of numerical simulation results and experimental data of jet time-averaged concentration on different downstream cross sections

2.2 模拟工况设置

振荡射流的影响因素包括受纳水体参数，为横流流速u0；射流本身的参数包括射流平均速度w0，振荡振幅wA，以及周期T(或频率f=1/T)。用斯特劳哈尔数St表示射流周期T的影响(式(6))。定义在一个周期内，t=1/4T为最大流速时刻，t=1/2T为速度逐渐减小的平均流速时刻，t=3/4T为最小流速时刻，t=T为速度逐渐增大的平均流速时刻。影响横流环境中振荡射流的因素有射流-横流速度比Rjc(式(7))、振幅-射流速度比Raj(式(8))以及斯特劳哈尔数St(式(6)))：

(6)

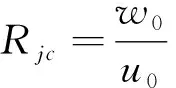
(7)

(8)

式中：d为射流口孔径，为0.01 m。

各组次的横流以及振荡射流的计算参数如表1所示。

表1 横流环境中振荡射流计算组次及参数

3 模拟结果与讨论

3.1 射流对称纵剖面特征

从相位平均流场与时均流场两个方面描述射流的对称纵剖面特征。

图3为NJ04组次4个典型相位下对称纵剖面(y/d=0)上射流相位平均流速场与浓度场。从图3可看出，在横流作用下，振荡射流呈现出明显的间歇性污染物云团现象，与波流环境中的非振荡射流[13]类似。间歇性污染物云团分别标记为A1～A3、B1～B3、C1～C3、D1～D3。A1-B1-C1-D1-A2可以看作在一个振荡周期内间歇性污染物云团的形成和发展过程。1/4T时刻冲击高度最小，弯曲程度最大，在这一阶段，射流柱随时间的推移而向上倾斜，污染物云团逐渐发展扩大；1/2T时刻射流速度减小，使得射流柱向下倾斜，当污染物云团向下游发展时，由于剪切层涡与横流之间发生卷吸效应，迎流侧剪切层涡扩大并变得不连贯；3/4T时刻冲击高度最大，弯曲程度最小，射流柱被横流冲击产生明显偏转；T时刻射流速度逐渐增大，射流柱逐渐向上倾斜。这一过程在每个循环中持续进行，与Shi等[18]的研究一致，振荡射流的存在使得污染物云团周期性地向下游传播。根据Hsu等[8]的研究，1/4T时刻为射流主导模式，1/2T时刻为过渡模式，3/4T时刻为下冲模式，T时刻为横流主导模式。

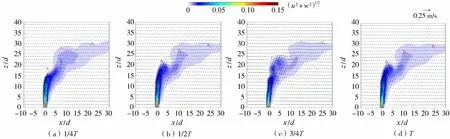
图3 NJ04组次4个典型相位对称纵剖面(y/d=0)上射流相位平均流速场和浓度场Fig.3 Phase-averaged flow velocity field and concentration field of jet on symmetrical longitudinal section(y/d=0) under four typical phases of group NJ04

图4是NJ00、NJ01、NJ02、NJ03组次对称纵剖面上射流的时均流速场与浓度场对比。相较于横流环境中的非振荡射流，振荡射流的间歇性污染物云团冲击高度更高，弯曲程度更大，表明振荡射流的扩散速度更快，分布宽度更大。随着射流振荡振幅和周期的增大，间歇性污染物云团冲击高度更高，弯曲程度减小。由于振荡射流增强了流场的非定常性，当射流-横流速度比相同时，振荡射流与横流的相互作用使得横流环境中振荡射流的时均速度矢量较非振荡射流向下弯曲，整个射流体更贴近底床，表明在射流周期性振荡的影响下，射流前行过程中的有效动量较无振荡时衰减得更快。另外，振荡作用(振幅与周期)的加强使射流轨迹摆动幅度增大，流线发生更加明显的弯曲，垂向平均流速衰减得更快。

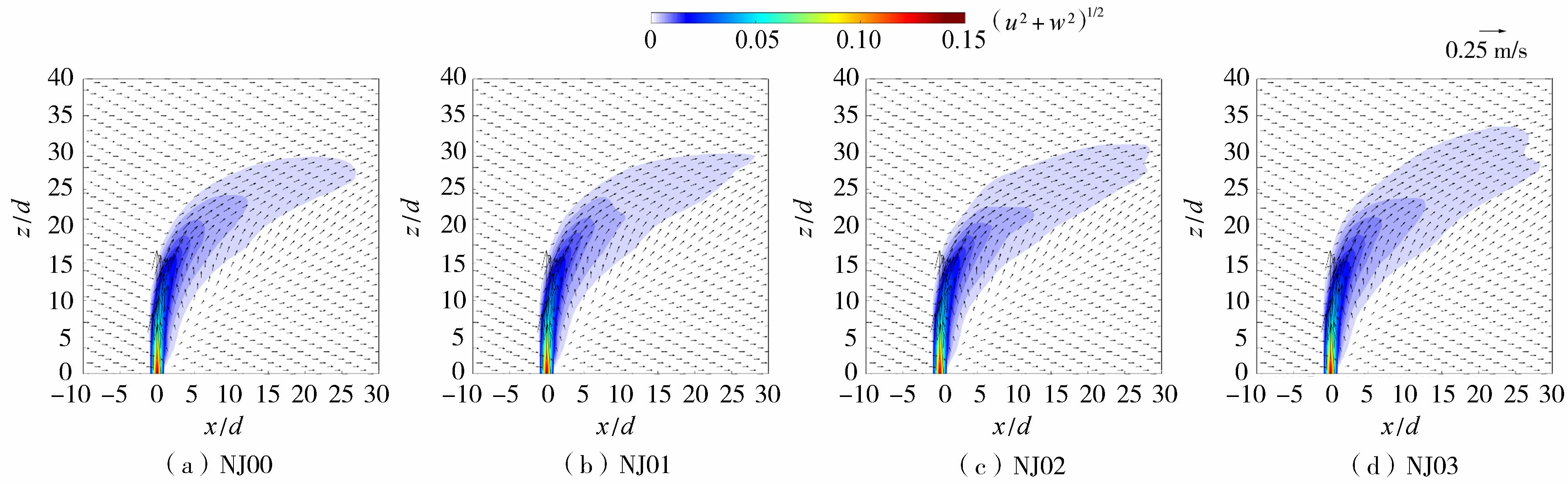
图4 4组次对称纵剖面(y/d=0)上射流时均流场和浓度场Fig.4 Time-averaged flow field and concentration field of jet on symmetrical longitudinal section(y/d=0) of four groups

图5为横流环境中非振荡射流与振荡射流的时均流速分布，两者的垂向流速基本呈现高斯分布。由图5可见，污染物在向下游传播的过程中，流速分布曲线的高斯分布更加明显，分布宽度变宽，最大流速值减小且其垂向位置逐渐变高。非振荡射流的最大流速均大于振荡射流的最大流速，而振荡射流的分布宽度明显大于非振荡射流，可见振荡作用引发的扩散效应显著。

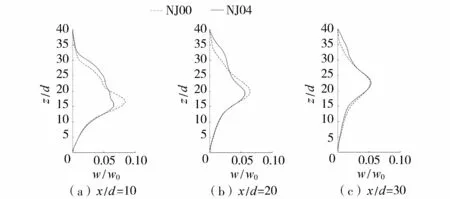
图5 横流环境中非振荡射流与振荡射流下游断面时均流速分布Fig.5 Time-averaged velocity distribution on downstream sections of non-oscillating jet and oscillating jet in cross flow environment

3.2 射流下游断面特征

图6分别为横流环境中非振荡射流与振荡射流(组次NJ00和组次NJ03)各下游断面上时均浓度场。从图6明显可以看出，振荡射流的存在使得射流在垂向上的宽度明显增加。

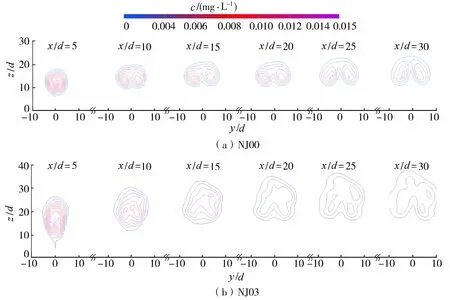
图6 横流环境中非振荡射流与振荡射流各下游断面上时均浓度场Fig.6 Time-averaged concentration fields of non-oscillating jet and oscillating jet at each downstream section in cross flow environment

横流环境中，由于CVP结构的存在，非振荡射流下游断面时均浓度有两个极大值；振荡射流除上述两个浓度极大值外，还存在一个由间歇性污染物云团引起的极大值。通过对比发现，振荡作用不仅使断面上时均浓度的最大值及其垂向位置发生变化，也使一定浓度包络线的面积发生了改变。为了对比各组次的稀释规律，采用断面浓度最大值Cm(或断面最小稀释度Sc)、断面浓度最大值Cm的垂向位置Zm、由0.25Cm等值线决定的射流可视范围(即宽度Rh和高度Rv)3个指标描述横流环境中射流下游断面上的浓度特征，如图7所示。最小稀释度公式为

(9)

式中C0为初始浓度。

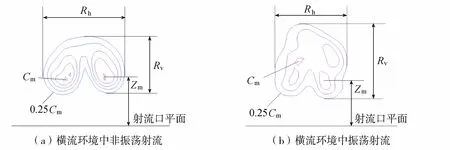
图7 描述横流环境中非振荡射流和振荡射流下游断面上浓度特征的指标Fig.7 Index to describe the concentration characteristics of non-oscillating jet and oscillating jet for downstream sections in cross flow environment

图8为NJ00、NJ01、NJ02、NJ03组次的稀释参数对比。与横流环境中非振荡射流相比，振荡射流的浓度最大值较小，即断面最小稀释度较大，最小稀释度垂向位置更靠近底床，断面可视范围面积显著增加。由此可见，振荡作用使得射流体与周围水体的相互作用加强，增强了射流的稀释能力；并且振荡作用增加了射流冲击高度，使得射流的影响范围变大，有利于射流与周围水体的混合。以断面最小稀释度为例，振荡射流(NJ03)与非振荡射流(NJ00)断面最小稀释度为35的水平位置分别为x/d=21和x/d=29，可见振荡作用使射流得到了更快的稀释。NJ01与NJ03的对比组也显示了与上述现象相似的规律，说明随着振幅的增大，射流的稀释能力也逐渐增强。

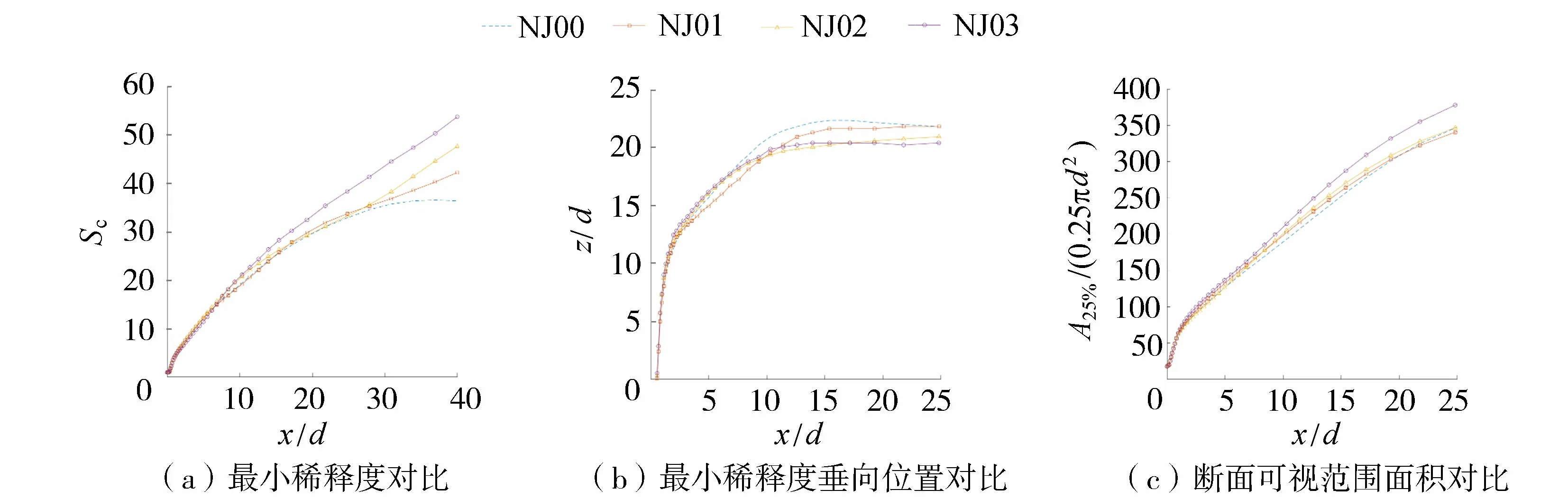
图8 各组次稀释度特性对比Fig.8 Comparison of dilution degree characteristics of each group

根据NJ01与NJ02对比斯特劳哈尔数(周期)的影响，从图8可以看到斯特劳哈尔数对最小稀释度影响较小，在距射流出口水平距离较小的位置(x/d<26)，两组射流的断面最小稀释度基本一样，之后发生一定变化——斯特劳哈尔数越小(周期越大)，最小稀释度越大。最小稀释度垂向位置与断面可视范围面积随着斯特劳哈尔数减小分别呈现出降低与增大的现象。总体来说，斯特劳哈尔数越小(周期越大)，振荡射流稀释效果越好。